4.2: Розв'язування лінійних систем шляхом заміщення
- Page ID
- 58253
Цілі навчання
- Вирішити лінійні системи за допомогою методу заміщення.
Метод заміщення
У цьому розділі ми визначимо повністю алгебраїчну техніку розв'язання систем. Ідея полягає в тому, щоб вирішити одне рівняння для однієї зі змінних і підставити результат в інше рівняння. Після виконання цього кроку підстановки нам залишиться єдине рівняння з однією змінною, яке можна вирішити за допомогою алгебри. Це називається методом підстановки, а кроки викладені в наступному прикладі.
Приклад\(\PageIndex{1}\)
Вирішити шляхом підміни:
Рішення:
Крок 1: Вирішіть для будь-якої змінної в будь-якому рівнянні. Якщо ви виберете перше рівняння, ви можете виділити\(y\) за один крок.
\(\begin{aligned} 2x+y&=7\\2x+y\color{Cerulean}{-2x}&=7\color{Cerulean}{-2x} \\ y&=-2x+7 \end{aligned}\)
Крок 2: Підставте вираз\(−2x+7\) для\(y\) змінної в інше рівняння.
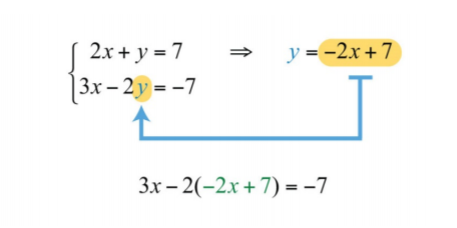.png)
Це залишає вам еквівалентне рівняння з однією змінною, яке можна вирішити за допомогою методів, вивчених до цього моменту.
Крок 3: Вирішіть для змінної, що залишилася. Щоб вирішити для\(x\), спочатку розподіліть\(−2\):
Крок 4: Назад підставляємо, щоб знайти значення іншої координати. \(x= 1\)Замініть будь-яке з вихідних рівнянь або їх еквівалентів. Зазвичай ми використовуємо еквівалентне рівняння, яке ми знайшли при виділенні змінної на кроці 1.
\(\begin{aligned} y&=-2x+7\\&=-2(\color{OliveGreen}{1}\color{black}{)+7}\\&=-2+7\\&=5 \end{aligned}\)
Рішення системи є\((1, 5)\). Обов'язково пред'явіть рішення у вигляді впорядкованої пари.
Крок 5: Перевірте. Переконайтеся, що ці координати вирішують обидва рівняння вихідної системи:
\(\color{Cerulean}{Check:}\:\:\color{black}{(1,5)}\)
\(\begin{array}{c|c} {Equation\:1:}&{Equation\:2:}\\{2x+y=7}&{3x-2y=-7}\\{2(\color{OliveGreen}{1}\color{black}{)+(}\color{OliveGreen}{5}\color{black}{)=7}}&{3(\color{OliveGreen}{1}\color{black}{)-2(}\color{OliveGreen}{5}\color{black}{)=-7}}\\{2+5=7}&{3-10=-7}\\{7=7\quad\color{Cerulean}{\checkmark}}&{-7=-7\quad\color{Cerulean}{\checkmark}} \end{array}\)
Графік цієї лінійної системи наступний:
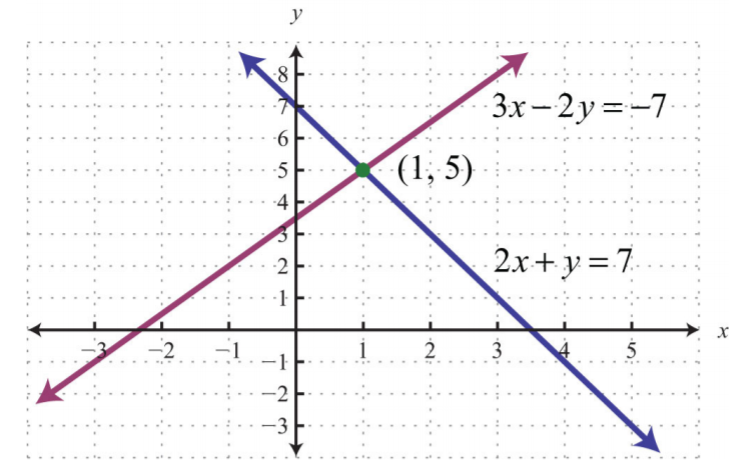.png)
Метод заміщення для розв'язання систем є повністю алгебраїчним методом. Таким чином, графічне зображення ліній не потрібно.
Відповідь:
\((1, 5)\)
Приклад\(\PageIndex{2}\)
Вирішити шляхом підміни:
\(\left\{\begin{aligned}2x−y&=1\\2x−y&=3\end{aligned}\right.\).
Рішення:
У цьому прикладі ми бачимо, що\(x\) має коефіцієнт\(1\) у другому рівнянні. Це говорить про те, що його можна виділити в один етап наступним чином:
\(\begin{aligned} x-y&=3 \\ x-y\color{Cerulean}{+y}&=3\color{Cerulean}{+y} \\ x&=3+y \end{aligned}\)
\(\left\{\begin{aligned} 2\color{Cerulean}{x}\color{black}{-y}&=12 \\ x-y&=3 \Rightarrow \color{Cerulean}{x}\color{black}{=3+y} \end{aligned} \right.\)
\(3+y\)Замініть\(x\) в першому рівнянні. Використовуйте дужки і подбайте про розподіл.
\(\begin{aligned} 2x-y&=12\\2(\color{OliveGreen}{3+y}\color{black}{)-y}&=12 \\6+2y-y&=12 \\6+y&=12 \\ 6+y\color{Cerulean}{-6}&=12\color{Cerulean}{-6}\\y&=6 \end{aligned}\)
Використовуйте\(x=3+y\) для пошуку\(x\).
\(\begin{aligned} x&=3+y\\&=3+\color{OliveGreen}{+6}\\&=9 \end{aligned}\)
Відповідь:
\((9, 6)\). Чек залишається на зчитувач.
Приклад\(\PageIndex{3}\)
Вирішити шляхом підміни:
\(\left\{\begin{aligned}3x−5y&=1\\7x&=−1\end{aligned}\right.\).
Рішення:
У цьому прикладі\(x\) змінна вже ізольована. Отже, ми можемо\(x=−1\) підставити в перше рівняння.
Відповідь:
\((−1, −4)\). Це хороша вправа для графіку цієї конкретної системи, щоб порівняти метод заміщення з методом графіки для розв'язування систем.
Вправа\(\PageIndex{1}\)
Вирішити шляхом підміни:
\(\left\{\begin{aligned}3x+y&=4\\8x+2y&=10\end{aligned}\right.\).
- Відповідь
-
\((1,1)\)
Розв'язування систем алгебраїчно часто вимагає роботи з дробами.
Приклад\(\PageIndex{4}\)
Вирішити шляхом підміни:
\(\left\{\begin{aligned}2x+8y&=5\\24x−4y&=−15\end{aligned}\right.\).
Рішення:
Почніть з вирішення for\(x\) в першому рівнянні.
\(\begin{aligned} 2x+8y&=5\\2x+8y\color{Cerulean}{-8y}&=5\color{Cerulean}{-8y} \\ \frac{2x}{\color{Cerulean}{2}}&=\frac{-8y+5}{\color{Cerulean}{2}} \\ x&=\frac{-8y}{2}+\frac{5}{2} \\ x&=-4y+\frac{5}{2} \end{aligned}\)
\(\left\{\begin{aligned} 2x+8y&=5 \Rightarrow \color{Cerulean}{x}\color{black}{=-4y+\frac{5}{2}} \\ 24\color{Cerulean}{x}\color{black}{-4y}&=-15\end{aligned}\right.\)
Далі підставляємо в друге рівняння і вирішуємо для\(y\).
Назад підставляємо в рівняння, яке використовується на етапі підстановки:
\(\begin{aligned} x&=-4y+\frac{5}{2} \\ &=-4\left(\color{OliveGreen}{\frac{3}{4}} \right)\color{black}{+\frac{5}{2}} \\ &=-3+\frac{5}{2} \\ &=-\frac{6}{2} + \frac{5}{2} \\ &=-\frac{1}{2} \end{aligned}\)
Відповідь:
\((-\frac{1}{2},\frac{3}{4})\)
Як ми знаємо, не всі лінійні системи мають лише одне впорядковане парне рішення. Нагадаємо, що деякі системи мають нескінченно багато упорядкованих парних рішень, а деякі не мають ніяких рішень. Далі ми вивчимо, що відбувається при використанні методу підстановки для вирішення залежної системи.
Приклад\(\PageIndex{5}\)
Вирішити шляхом підміни:
\(\left\{\begin{aligned}−5x+y&=−1\\10x−2y&=2\end{aligned}\right.\).
Рішення:
Оскільки перше рівняння має термін з коефіцієнтом\(1\), ми вирішуємо для цього спочатку.
Далі підставляємо цей вираз у for\(y\) у другому рівнянні.
\(\begin{aligned} 10x-2y&=2 \\ 10x-2(\color{OliveGreen}{5x-1}\color{black}{)}&=2 \\ 10x-10x+2&=2 \\ 2&=2 \quad\color{Cerulean}{True} \end{aligned}\)
Цей процес призвів до істинного твердження; отже, рівняння є ідентичністю, а будь-яке дійсне число - це рішення. Це говорить про те, що система залежна. Одночасні рішення набувають вигляду\((x, mx + b)\), або в даному випадку\((x, 5x − 1)\), де\(x\) знаходиться будь-яке дійсне число.
Відповідь:
\((x, 5x−1)\)
Щоб краще зрозуміти попередній приклад, перепишіть обидва рівняння у формі нахилу-перехоплення і побудуйте їх на одному наборі осей.
Ми бачимо, що обидва рівняння представляють одну і ту ж лінію, і, таким чином, система залежить. Тепер вивчіть, що відбувається при вирішенні неузгодженої системи методом підстановки.
Приклад\(\PageIndex{6}\)
Вирішити шляхом підміни:
\(\left\{\begin{aligned}−7x+3y&=3\\14x−6y&=−16\end{aligned}\right.\).
Рішення:
Вирішити для\(y\) в першому рівнянні.
\(\begin{aligned} -7x+3y&=3 \\ -7x+3y\color{Cerulean}{+7x}&=3\color{Cerulean}{+7x} \\3y&=7x+3 \\ \frac{3y}{\color{Cerulean}{3}}&=\frac{7x+3}{\color{Cerulean}{3}}\\y&=\frac{7}{3}x+1 \end{aligned}\)
\(\left\{\begin{aligned} -7x+3y&=3 \Rightarrow \color{Cerulean}{y}\color{black}{=\frac{7}{3}x+1} \\ 14x-6\color{Cerulean}{y}&=-16\end{aligned}\right.\)
Підставляємо в друге рівняння і вирішуємо.
Рішення призводить до помилкового твердження. Це говорить про те, що рівняння є протиріччям. Там немає рішення для\(x\) і, отже, немає рішення для системи.
Відповідь:
Немає рішення,\(Ø\)
Помилкове твердження вказує на те, що система непослідовна, або в геометричному плані, що лінії паралельні і не перетинаються. Щоб проілюструвати це, визначте форму нахилу-перехоплення кожної лінії і намалюйте їх на одному і тому ж наборі осей.
У формі нахилу перехоплення легко побачити, що дві лінії мають однаковий нахил, але різні\(y\) -перехоплення.
Вправа\(\PageIndex{2}\)
Вирішити шляхом підміни:
\(\left\{\begin{aligned}2x−5y&=3\\4x−10y&=6\end{aligned}\right.\).
- Відповідь
-
\((x, \frac{2}{5}x−\frac{3}{5}) \)
Ключові виноси
- Метод заміщення є повністю алгебраїчним методом розв'язання системи рівнянь.
- Метод підстановки вимагає, щоб ми розв'язали одну зі змінних, а потім підставляємо результат в інше рівняння. Після виконання кроку підстановки отримане рівняння має одну змінну і може бути вирішене за допомогою методів, вивчених до цього моменту.
- Коли значення однієї зі змінних визначено, поверніться назад і підставляйте його в одне з вихідних рівнянь, або їх еквівалентні рівняння, щоб визначити відповідне значення іншої змінної.
- Розв'язки систем двох лінійних рівнянь з двома змінними, якщо вони існують, є впорядкованими парами\((x, y)\).
- Якщо процес розв'язання системи рівнянь призводить до помилкового твердження, то система непослідовна і рішення немає,\(Ø\).
- Якщо процес розв'язання системи рівнянь призводить до істинного твердження, то система залежна і існує нескінченно багато рішень, які можна виразити за допомогою форми\((x, mx + b)\).
Вправа\(\PageIndex{3}\) Substitution Method
Вирішити шляхом підміни.
- \(\left\{\begin{aligned} y&=4x−1\\−3x+y&=1\end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=3x−8\\4x−y&=2 \end{aligned}\right.\)
- \(\left\{\begin{aligned}x&=2y−3\\x+3y&=−8 \end{aligned}\right.\)
- \(\left\{\begin{aligned}x&=−4y+12\\x+3y&=12 \end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=3x−5\\x+2y&=2 \end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=x\\2x+3y&=10 \end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=4x+1\\−4x+y&=2 \end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=−3x+5\\3x+y&=5 \end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=2x+3\\2x−y&=−3 \end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=5x−1\\x−2y&=5 \end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=−7x+1\\3x−y&=4 \end{aligned}\right.\)
- \(\left\{\begin{aligned}x&=6y+2\\5x−2y&=0 \end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=−2−2x\\−y&=−6 \end{aligned}\right.\)
- \(\left\{\begin{aligned}x&=−3x−4\\y&=−3 \end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=−\frac{1}{5}x+\frac{3}{7}\\x−5y&=9 \end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=\frac{2}{3}x−\frac{1}{6}\\x−9y&=0 \end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=\frac{1}{2}x+\frac{1}{3}\\x−6y&=4 \end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=−\frac{3}{8}x+\frac{1}{2}\\2x+4y&=1 \end{aligned}\right.\)
- \(\left\{\begin{aligned}x+y&=6\\2x+3y=\frac{1}{6} \end{aligned}\right.\)
- \(\left\{\begin{aligned}x−y&=3\\−2x+3y&=−2 \end{aligned}\right.\)
- \(\left\{\begin{aligned}2x+y&=2\\3x−2y&=\frac{1}{7} \end{aligned}\right.\)
- \(\left\{\begin{aligned}x−3y&=−\frac{1}{13}\\x+5y&=−5 \end{aligned}\right.\)
- \(\left\{\begin{aligned}x+2y&=−3\\3x−4y&=−2 \end{aligned}\right.\)
- \(\left\{\begin{aligned}5x−y&=12\\9x−y&=10 \end{aligned}\right.\)
- \(\left\{\begin{aligned}x+2y&=−6\\−4x−8y&=24 \end{aligned}\right.\)
- \(\left\{\begin{aligned}x+3y&=−6\\−2x−6y&=−12 \end{aligned}\right.\)
- \(\left\{\begin{aligned}−3x+y&=−4\\6x−2y&=−2 \end{aligned}\right.\)
- \(\left\{\begin{aligned}x−5y&=−10\\2x−10y&=−20 \end{aligned}\right.\)
- \(\left\{\begin{aligned}3x−y&=9\\4x+3y&=−1 \end{aligned}\right.\)
- \(\left\{\begin{aligned}2x−y&=5\\4x+2y&=−2 \end{aligned}\right.\)
- \(\left\{\begin{aligned}−x+4y&=0\\2x−5y&=−6 \end{aligned}\right.\)
- \(\left\{\begin{aligned}3y−x&=5\\5x+2y&=−8 \end{aligned}\right.\)
- \(\left\{\begin{aligned}2x−5y&=1\\4x+10y&=2 \end{aligned}\right.\)
- \(\left\{\begin{aligned}3x−7y&=−3\\6x+14y&=0 \end{aligned}\right.\)
- \(\left\{\begin{aligned}10x−y&=3\\−5x+12y&=1 \end{aligned}\right.\)
- \(\left\{\begin{aligned}−\frac{1}{3}x+\frac{1}{6}y&=\frac{2}{3}\\ \frac{1}{2}x−\frac{1}{3}y&=−\frac{3}{2} \end{aligned}\right.\)
- \(\left\{\begin{aligned}\frac{1}{3}x+\frac{2}{3}y&=1 \\ \frac{1}{4}x−\frac{1}{3}y&=−\frac{1}{12} \end{aligned}\right.\)
- \(\left\{\begin{aligned}\frac{1}{7}x−y&=\frac{1}{2}\\ \frac{1}{4}x+\frac{1}{2}y&=2 \end{aligned}\right.\)
- \(\left\{\begin{aligned}−\frac{3}{5}x+\frac{2}{5}y&=\frac{1}{2}\\ \frac{1}{3}x−\frac{1}{12}y&=−\frac{1}{3} \end{aligned}\right.\)
- \(\left\{\begin{aligned}\frac{1}{2}x&=\frac{2}{3}y\\x−\frac{2}{3}y&=2 \end{aligned}\right.\)
- \(\left\{\begin{aligned}−\frac{1}{2}x+\frac{1}{2}y&=\frac{5}{8} \\ \frac{1}{4}x+\frac{1}{2}y&=\frac{1}{4} \end{aligned}\right.\)
- \(\left\{\begin{aligned}x−y&=0\\−x+2y&=3 \end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=3x\\2x−3y&=0 \end{aligned}\right.\)
- \(\left\{\begin{aligned}2x+3y&=18\\−6x+3y&=−6 \end{aligned}\right.\)
- \(\left\{\begin{aligned}−3x+4y&=20\\ 2x+8y&=8 \end{aligned}\right.\)
- \(\left\{\begin{aligned}5x−3y&=−1\\ 3x+2y&=7 \end{aligned}\right.\)
- \(\left\{\begin{aligned}−3x+7y&=2\\ 2x+7y&=1 \end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=3\\y&=−3 \end{aligned}\right.\)
- \(\left\{\begin{aligned}x&=5\\x&=−2 \end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=4\\y&=4\end{aligned}\right.\)
- Відповідь
-
1. \((2, 7)\)
3. \((−5, −1)\)
5. \((2, 6)\)
7. \(∅\)
9. \((x, 2x+3)\)
11. \((\frac{1}{2}, −\frac{5}{2})\)
13. \((4, −2)\)
15. \((3, \frac{12}{5})\)
17. \((−3, −\frac{7}{6})\)
19. \((2, 4)\)
21. \((3, −4)\)
23. \((−\frac{8}{5}, −\frac{7}{10})\)
25. \((x, −\frac{1}{2}x−3)\)
27. \(∅\)
29. \((2, −3)\)
31. \((−8, −2)\)
33. \((\frac{1}{2}, 0)\)
35. \(∅\)
37. \((1, 1)\)
39. \((−\frac{11}{10}, −\frac{2}{5})\)
41. \((−\frac{1}{2}, \frac{3}{4})\)
43. \((0, 0)\)
45. \((−4, 2)\)
47. \((−\frac{1}{5}, \frac{1}{5})\)
49. \(∅\)
Вправа\(\PageIndex{4}\) Substitution Method
Налаштуйте лінійну систему і вирішуйте її за допомогою методу підстановки.
- Сума двох чисел дорівнює\(19\). Чим більше число\(1\) менше, ніж в три рази, тим менше.
- Сума двох чисел дорівнює\(15\). Чим\(3\) більше в два рази менше.
- Різниця двох чисел є\(7\) і їх сума дорівнює\(1\).
- Різниця двох чисел є\(3\) і їх сума дорівнює\(−7\).
- Де на графіку\(−5x+3y=30\)\(x\) -координата дорівнює\(y\) -координаті?
- Де на графіку\(\frac{1}{2}x−\frac{1}{3}y=1\)\(x\) -координата дорівнює\(y\) -координаті?
- Відповідь
-
1. Два числа -\(5\) і\(14\).
3. Два числа -\(4\) і\(−3\).
5. \((−\frac{1}{5}, −\frac{1}{5})\)
Вправа\(\PageIndex{5}\) Discussion Board Topics
- Опишіть, що призводить до вибору змінної для вирішення при початку процесу розв'язання шляхом підстановки.
- Обговоріть переваги і недоліки методу заміщення.
- Відповідь
-
1. Відповіді можуть відрізнятися
