6.5: Розв'язування квадратичних нерівностей
- Page ID
- 58356
Цілі навчання
- Перевірте розв'язки квадратичних нерівностей однією змінною.
- Зрозумійте геометричну залежність між розв'язками квадратичних нерівностей та їх графіками.
- Розв'яжіть квадратичні нерівності.
Розв'язки квадратичних нерівностей
Квадратична нерівність 15 - це математичне твердження, яке пов'язує квадратичний вираз як менший або більший за інший. Нижче наведено кілька прикладів квадратичних нерівностей, розв'язаних у цьому розділі.
| \(x^{2}-2 x-11 \leq 0\) | \(2 x^{2}-7 x+3>0\) | \(9-x^{2}>0\) |
Розв'язок квадратичної нерівності - це дійсне число, яке видасть справжнє твердження при заміні змінної.
Приклад\(\PageIndex{1}\):
Є\(-3\)\(-2\), і\(-1\) рішення для\(x^{2}-x-6 \leq 0 \)?
Рішення
Підставити задане значення в for\(x\) і спростити.
\(\begin{array} {r | r | r} {x^{2}-x-6\leq0}&{x^{2}-x-6\leq0}&{x^{2}-x-6\leq0} \\ {(\color{OliveGreen}{-3}\color{black}{)}^{2}-(\color{OliveGreen}{-3}\color{black}{)}-6\leq0}&{(\color{OliveGreen}{-2}\color{black}{)}^{2}-(\color{OliveGreen}{-2}\color{black}{)}-6\leq0}&{(\color{OliveGreen}{-1}\color{black}{)}^{2}-(\color{OliveGreen}{-1}\color{black}{)}-6\leq0} \\ {9+3-6\leq0}&{4+2-6\leq0}&{1+1-6\leq0} \\ {6\leq0\:\:\color{red}{✗}}&{0\leq0\:\:\color{Cerulean}{✓}}&{-4\leq0\:\:\color{Cerulean}{✓}} \end{array}\)
Відповідь:
\(-2\)і\(-1\) є рішеннями і не\(-3\) є.
Квадратичні нерівності можуть мати нескінченно багато розв'язків, одне рішення або відсутність рішення. Якщо розв'язків нескінченно багато, графуйте розв'язку, встановлене на числовому рядку і/або висловіть рішення за допомогою інтервальних позначень. Графік функції, визначеної\(f (x) = x^{2} − x − 6\) знайденим у попередньому прикладі, ми маємо
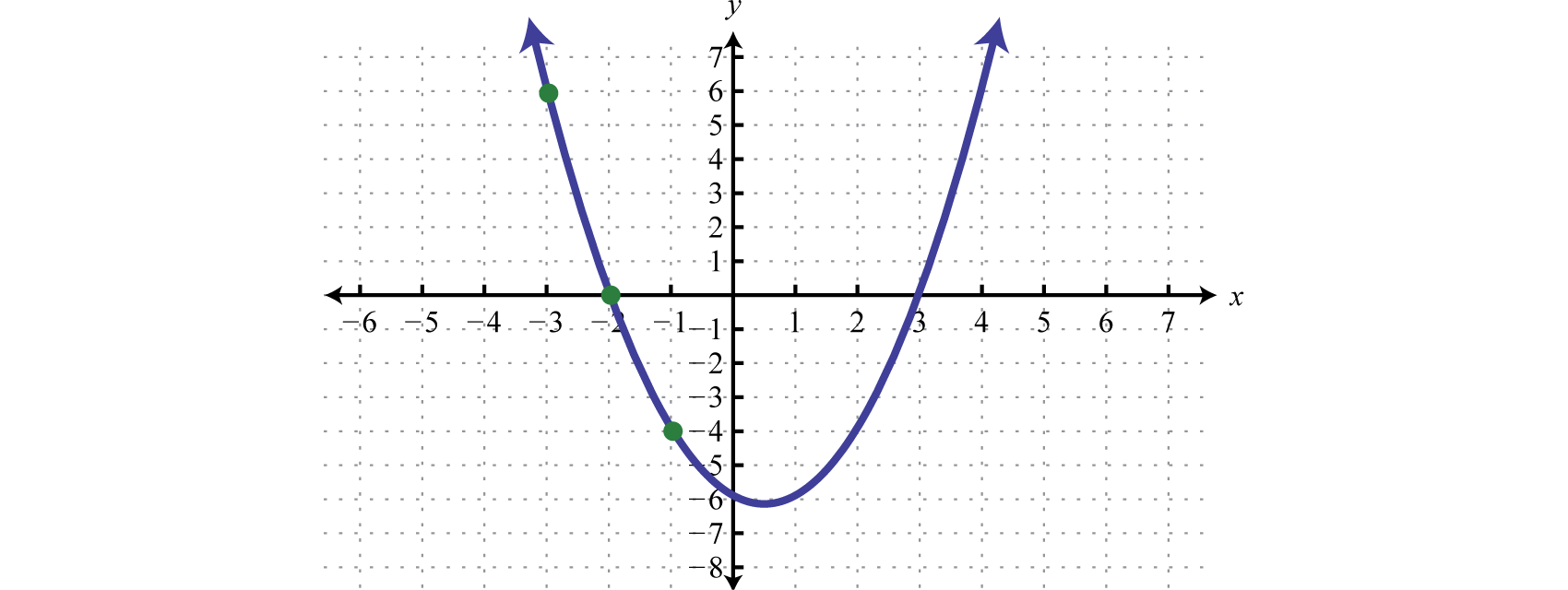
Результат оцінки для будь-якого\(x\) -значення буде від'ємним, нульовим або позитивним.
\(\begin{aligned} f(-3)&=6 &\color{Cerulean}{Positive \:f(x)>0} \\ f(-2)&=0 &\color{Cerulean}{Zero \:f(x)\:=0} \\f(-1)&=-4 &\color{Cerulean}{Negative \:f(x)<0} \end{aligned}\)
Значення в області функції, що відокремлюють області, що дають позитивні або негативні результати, називаються критичними числами 16. У випадку квадратичної функції критичними числами є коріння, іноді звані нулями. Наприклад,\(f (x) = x^{2} − x − 6 = (x + 2) (x − 3)\) має коріння\(−2\) і\(3\). Ці значення пов'язують області, де функція є додатною (над\(x\) віссю -) або від'ємною (нижче\(x\) -осі).
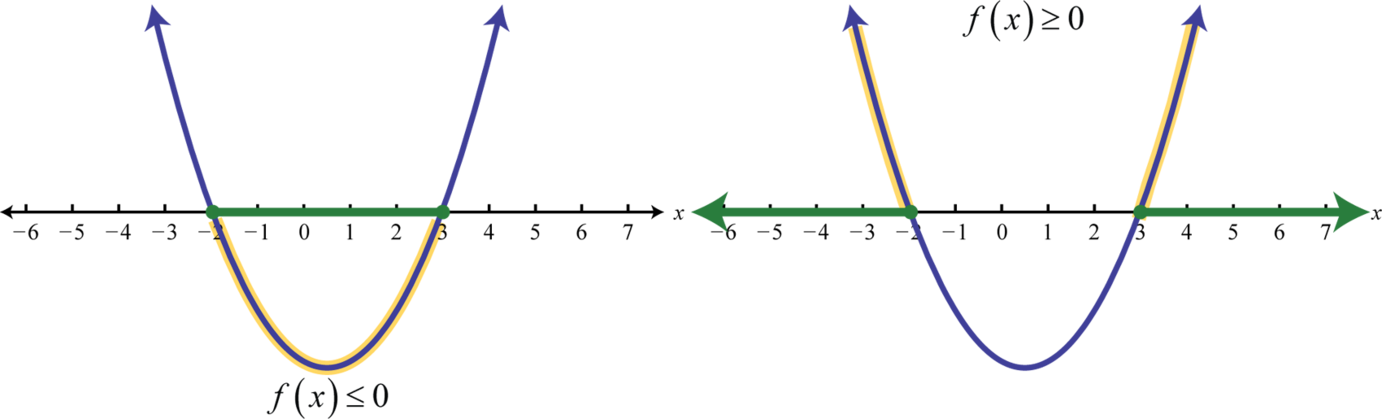
Тому\(x^{2} − x − 6 ≤ 0\) має рішення де\(−2 ≤ x ≤ 3\), використовуючи інтервальні позначення\([−2, 3]\). Крім того,\(x^{2} − x − 6 ≥ 0\) має рішення де\(x ≤ −2\) або\(x ≥ 3\), використовуючи інтервальні позначення\((−∞, −2] ∪ [−3, ∞)\).
Приклад\(\PageIndex{2}\):
За даними графіка\(f\) визначають розв'язки для\(f(x)>0\):
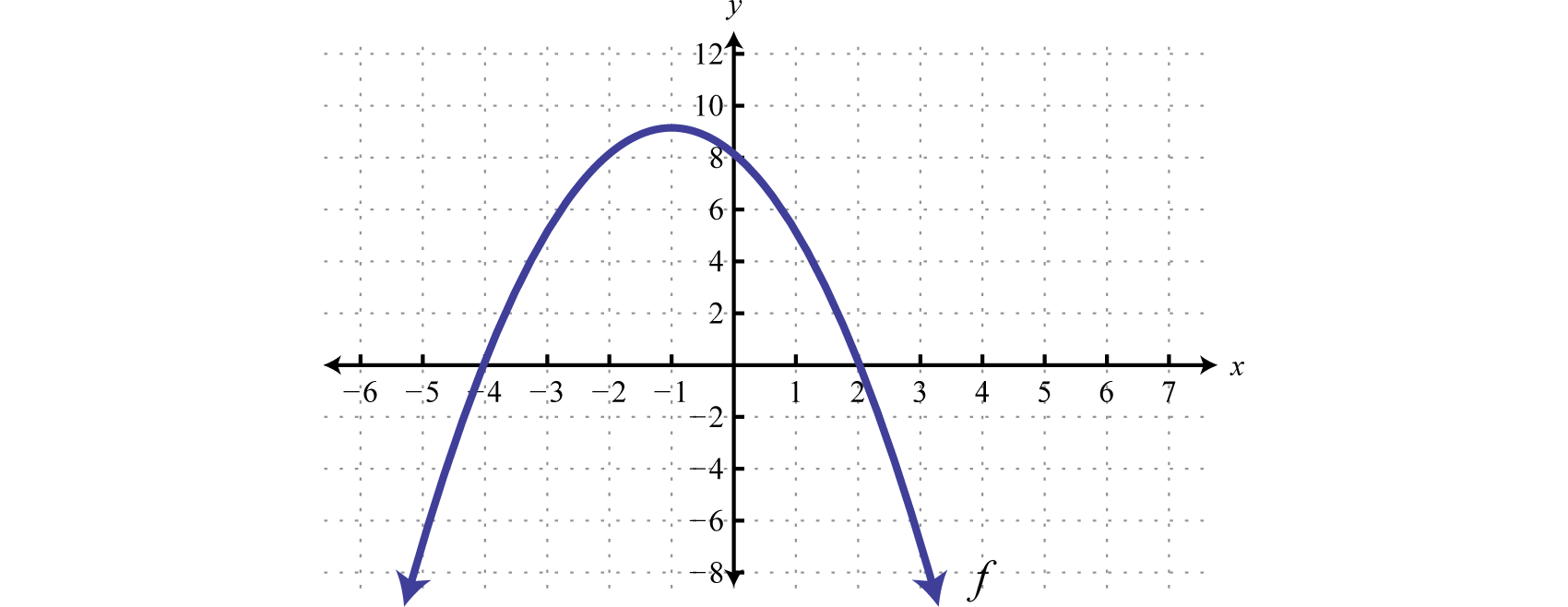
Через сувору нерівність набір розв'язків затінюється відкритою крапкою на кожній з меж. Це вказує на те, що ці критичні числа фактично не включені в набір рішень. Цей набір рішень може бути виражений двома способами,
\(\begin{aligned}\{x |-4<&x<2\} &\color{Cerulean} { Set\: Notation } \\ (-4,&2) &\color{Cerulean} { Interval\: Notation }\end{aligned}\)
У цьому підручнику ми продовжимо подавати відповіді в інтервальних позначеннях.
Відповідь:
\((-4,2)\)
Вправа\(\PageIndex{1}\)
За даними графіка\(f\) визначають розв'язки для\(f (x) < 0\):
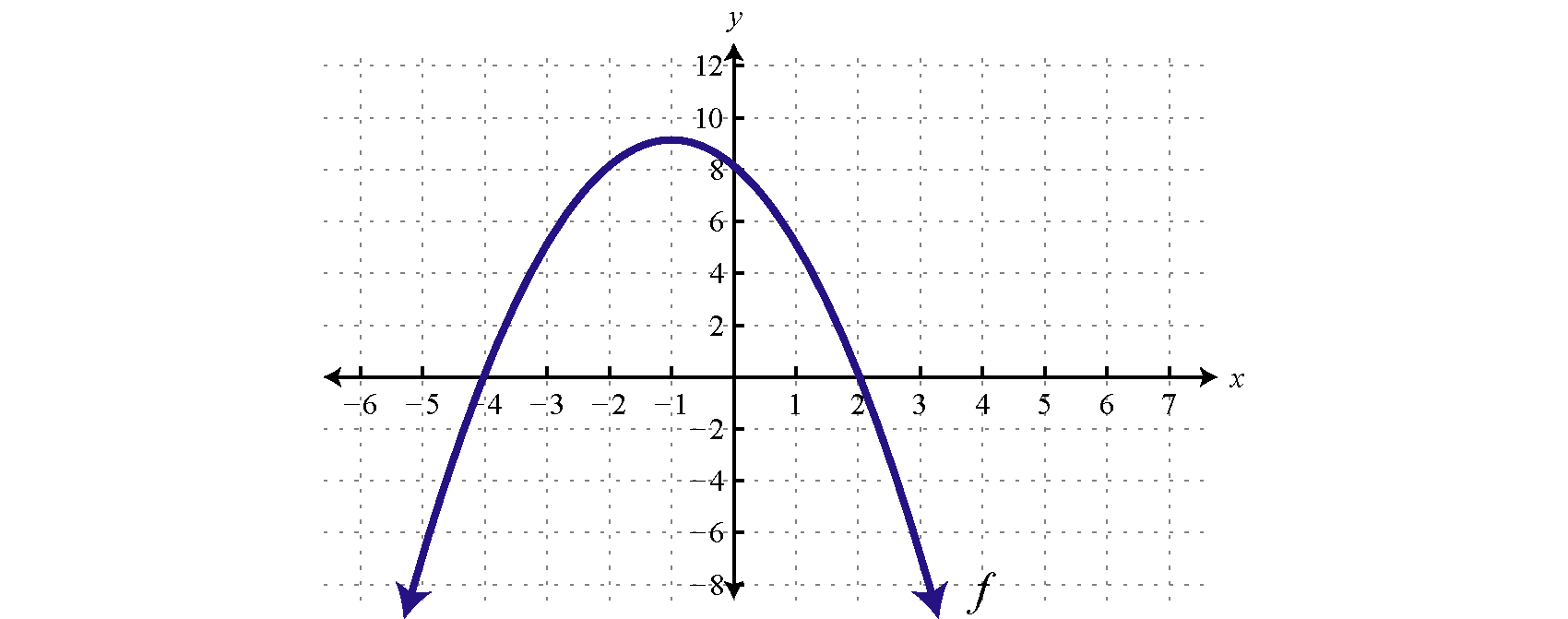
- Відповідь
-
\((-\infty,-4) \cup(2, \infty)\)
www.youtube.com/В/ККБАОМ8Бубо
Розв'язування квадратичних нерівностей
Далі ми окреслимо техніку, яка використовується для розв'язання квадратичних нерівностей без графіків параболи. Для цього ми використовуємо знакову діаграму 17, яка моделює функцію, використовуючи числову лінію, яка представляє\(x\) -вісь та знаки,\((+\) або\(−)\) для вказівки, де функція є позитивною чи негативною. Наприклад,
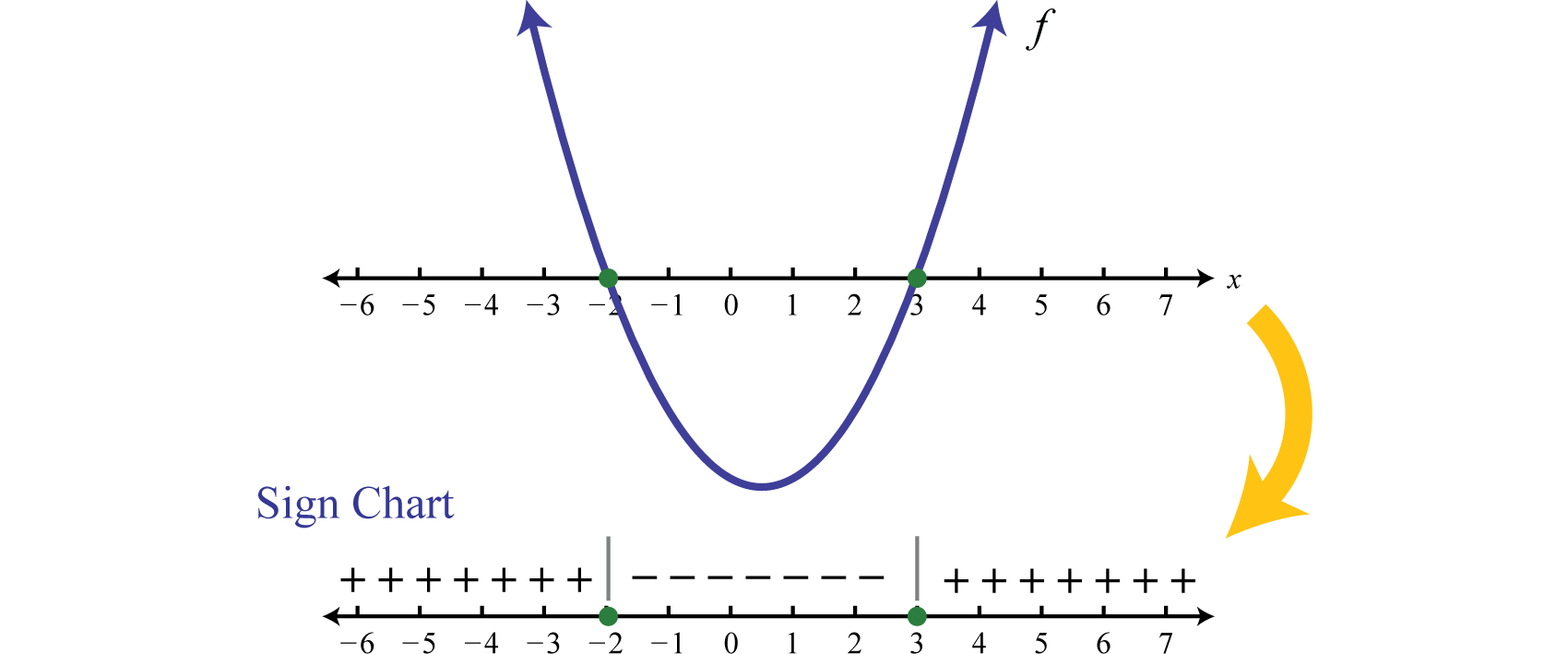
Знаки плюса вказують на те, що функція позитивна на регіон. Негативні ознаки вказують на те, що функція негативна на регіон. Межами виступають критичні числа,\(−2\) і\(3\) в даному випадку. Знакові діаграми корисні, коли детальне зображення графіка не потрібно і широко використовуються в математиці вищого рівня. Етапи розв'язання квадратичної нерівності з однією змінною викладені в наступному прикладі.
Приклад\(\PageIndex{3}\):
Вирішити:\(-x^{2}+6 x+7 \geq 0\).
Рішення
Важливо відзначити, що ця квадратична нерівність знаходиться в стандартній формі, з нулем на одній стороні нерівності.
Крок 1: Визначте критичні цифри. Для квадратичної нерівності в стандартній формі критичні числа є корінням. Тому встановіть функцію рівну нулю і вирішуйте.
\(-x^{2}+6 x+7=0 \)
\(-\left(x^{2}-6 x-7\right)=0 \)
\(-(x+1)(x-7)=0 \)
\(\begin{aligned}x+1&=0 \:\:\:\:\text { or } &x-7=0 \\ x&=-1 &x=7\end{aligned}\)
Критичними числами є\(-1\) і\(7\).
Крок 2: Створіть діаграму знаків. Оскільки критичні числа пов'язують області, де функція є позитивною або від'ємною, нам потрібно перевірити лише одне значення в кожній області. У цьому випадку критичні числа розділяють числовий рядок на три області, і ми вибираємо тестові значення\(x = −3, x = 0\), і\(x = 10\).
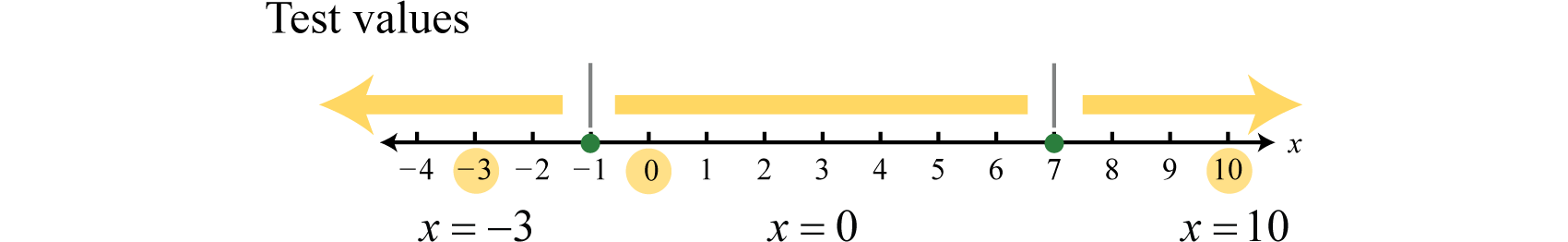
Значення тесту можуть відрізнятися. Насправді нам потрібно лише визначити ознаку\((+\) або\(−)\) результат при оцінці\(f (x) = −x^{2} + 6x + 7 = − (x + 1) (x − 7)\). Тут ми оцінюємо за допомогою факторної форми.
\(\begin{aligned} f(\color{OliveGreen}{-3}\color{black}{)}&=-(\color{OliveGreen}{-3}\color{black}{+}1)(\color{OliveGreen}{-3}\color{black}{-}7) =-(-2)(-10)&=-\color{Cerulean} {Negative} \\ f(\color{OliveGreen}{0}\color{black}{)}&=-(\color{OliveGreen}{0}\color{black}{+}1)(\color{OliveGreen}{0}\color{black}{-}7) =-(1)(-7)&=+\color{Cerulean} { Positive } \\ f(\color{OliveGreen}{10}\color{black}{)}&=-(\color{OliveGreen}{10}\color{black}{+}1)(\color{OliveGreen}{10}\color{black}{-}7) =-(11)(3)&=-\color{Cerulean} {Negative} \end{aligned}\)
Оскільки результат оцінки для\(−3\) був негативним, ми ставимо негативні знаки вище першого регіону. Результат оцінки для\(0\) був позитивним, тому ми розміщуємо позитивні знаки вище середньої області. Нарешті, результат оцінки для\(10\) був негативним, тому ми розміщуємо негативні знаки над останньою областю, і діаграма знаків завершена.
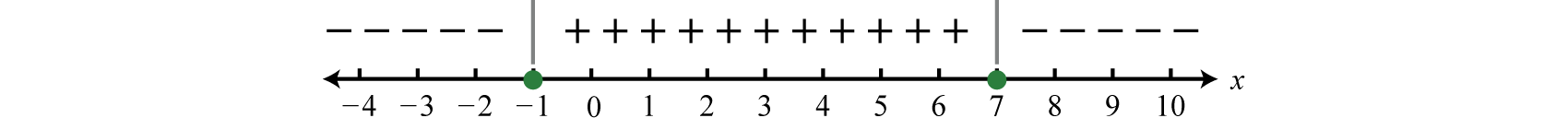
Крок 3: Використовуйте діаграму знаків, щоб відповісти на питання. У цьому випадку нас просять визначити де\(f (x) ≥ 0\), або де функція додатна або нуль. З діаграми знаків ми бачимо, що це відбувається, коли\(x\) -значення включені між\(−1\) і\(7\).

Використовуючи інтервальне позначення, затінена область виражається як\([−1, 7]\). Графік не обов'язковий, однак для повноти він наведений нижче.
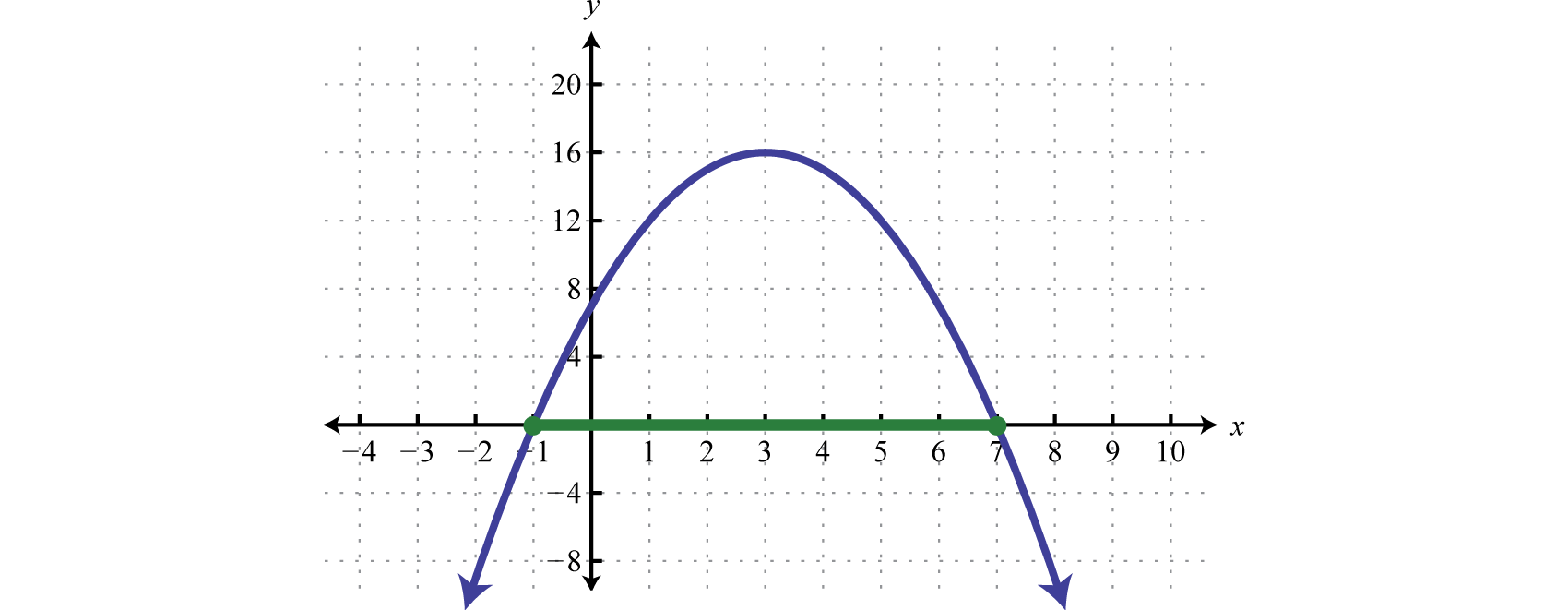
Дійсно функція більше або дорівнює нулю, вище або на\(x\) -осі, для\(x\) -значень в заданому інтервалі.
Відповідь:
\([-1,7]\)
Приклад\(\PageIndex{4}\):
Вирішити:\(2 x^{2}-7 x+3>0\).
Рішення
Почніть з знаходження критичних чисел, в даному випадку коренів\(f(x)=2 x^{2}-7 x+3\).
\(\begin{aligned}2 x^{2}-7 x+3&=0 \\ (2 x-1)(x-3)&=0\end{aligned}\)
\(\begin{aligned} 2 x-1 &=0 \:\:\:\:\:\text { or }& x-3=0 \\ 2 x &=1 \quad &x=3 \\ x &=\frac{1}{2} \end{aligned}\)
Критичними числами є\(\frac{1}{2}\) і\(3\). Через сувору нерівність > ми будемо використовувати відкриті точки.

Далі вибираємо тестове значення в кожному регіоні і визначаємо знак після оцінки\(f (x) = 2x^{2} − 7x + 3 = (2x − 1) (x − 3)\). Тут вибираємо тестові значення\(−1, 2\), і\(5\).
\(\begin{aligned} f(\color{OliveGreen}{-1}\color{black}{)} &=[2(\color{OliveGreen}{-1}\color{black}{)}-1](\color{OliveGreen}{-1}\color{black}{-}3)&=(-)(-)=+\\ f(\color{OliveGreen}{2}\color{black}{)} &=[2(\color{OliveGreen}{2}\color{black}{)}-1](\color{OliveGreen}{2}\color{black}{-}3)&=(+)(-)=-\\ f(\color{OliveGreen}{5}\color{black}{)} &=[2(\color{OliveGreen}{5}\color{black}{)}-1](\color{OliveGreen}{5}\color{black}{-}3)&=(+)(+)=+\end{aligned}\)
І ми можемо заповнити таблицю знаків.

Питання просить нас знайти\(x\) -значення, які дають позитивні результати (більше нуля). Тому затінюйте в регіонах з\(+\) над ними. Це набір рішень.

Відповідь:
\(\left(-\infty, \frac{1}{2}\right) \cup(3, \infty)\)
Іноді квадратична функція не фактор. У цьому випадку ми можемо скористатися квадратичною формулою.
Приклад\(\PageIndex{5}\):
Вирішити:\(x^{2}-2 x-11 \leq 0\)
Рішення
Знайдіть критичні цифри.
\(x^{2}-2 x-11=0\)
Визначте\(a, b\), і\(c\) для використання в квадратичній формулі. Ось\(a = 1, b = −2\), і\(c = −11\). Підставте відповідні значення в квадратичну формулу, а потім спростіть.
\(\begin{aligned} x &=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \\ &=\frac{-(\color{OliveGreen}{-2}\color{black}{)} \pm \sqrt{(\color{OliveGreen}{-2}\color{black}{)}^{2}-4(\color{OliveGreen}{1}\color{black}{)}(\color{OliveGreen}{-11}\color{black}{)}}}{2(\color{OliveGreen}{1}\color{black}{)}} \\ &=\frac{2 \pm \sqrt{48}}{2} \\ &=\frac{2 \pm 4 \sqrt{3}}{2} \\ &=1 \pm 2 \sqrt{3} \end{aligned}\)
Тому критичними числами є\(1-2 \sqrt{3} \approx-2.5\) і\(1+2 \sqrt{3} \approx 4.5\). Використовуйте замкнуту крапку на цифрі, щоб вказати, що ці значення будуть включені до набору розв'язків.

Тут ми будемо використовувати тестові значення\(−5, 0\), і\(7\).
\(\begin{aligned} f(\color{OliveGreen}{-5}\color{black}{)}&=(\color{OliveGreen}{-5}\color{black}{)}^{2}-2(\color{OliveGreen}{-5}\color{black}{)}-11 =25+10-11&=+\\ f(\color{OliveGreen}{0}\color{black}{)}&=(\color{OliveGreen}{0}\color{black}{)}^{2}-2(\color{OliveGreen}{0}\color{black}{)}-11 =0+0-11&=-\\ f(\color{OliveGreen}{7}\color{black}{)}&=(\color{OliveGreen}{7}\color{black}{)}^{2}-2(\color{OliveGreen}{7}\color{black}{)}-11 =49-14-11&=+\end{aligned}\)
Після завершення знакової діаграми затінюйте значення, де функція від'ємна, як зазначено в питанні\((f (x) ≤ 0)\).

Відповідь:
\([1-2 \sqrt{3}, 1+2 \sqrt{3}]\)
Вправа\(\PageIndex{2}\)
Вирішити:\(9-x^{2}>0\).
- Відповідь
-
\((-3,3)\)
www.youtube.com/В/7ГМ8 Гуваса
Може бути так, що критичних цифр немає.
Приклад\(\PageIndex{6}\):
Вирішити:\(x^{2}-2 x+3>0\).
Рішення
Щоб знайти критичні числа вирішувати,
\(x^{2}-2 x+3=0\)
Підставляємо\(a = 1, b = −2\), а\(c = 3\) в квадратичну формулу і потім спрощуємо.
\(\begin{aligned} x &=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \\ &=\frac{-(\color{OliveGreen}{-2}\color{black}{)} \pm \sqrt{(\color{OliveGreen}{-2}\color{black}{)}^{2}-4(\color{OliveGreen}{1}\color{black}{)}(\color{OliveGreen}{3}\color{black}{)}}}{2(\color{OliveGreen}{1}\color{black}{)}} \\ &=\frac{2 \pm \sqrt{-8}}{2} \\ &=\frac{2 \pm 2 i \sqrt{2}}{2} \\ &=1+i \sqrt{2} \end{aligned}\)
Оскільки рішення не є реальними, ми робимо висновок, що реальних коренів немає; отже, немає критичних чисел. Коли це так, графік не має\(x\) -перехоплює і повністю знаходиться вище або нижче\(x\) -осі. Ми можемо протестувати будь-яке значення, щоб створити діаграму знаків. Тут вибираємо\(x = 0\).
\(f(0)=(0)^{2}-2(0)+3=+\)
Оскільки тестове значення дало позитивний результат, діаграма знаків виглядає наступним чином:
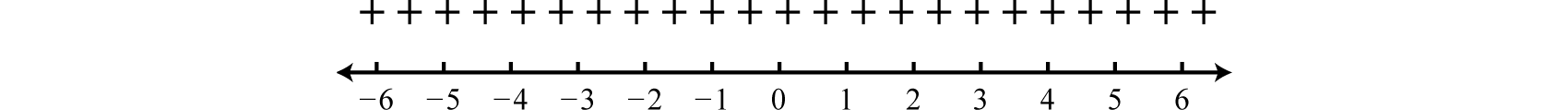
Шукаємо значення де\(f (x) > 0\); знакова діаграма означає, що будь-яке дійсне число для\(x\) задовольнить цю умову.

Відповідь:
\((-\infty, \infty)\)
Функція в попередньому прикладі наведена на графіку нижче.
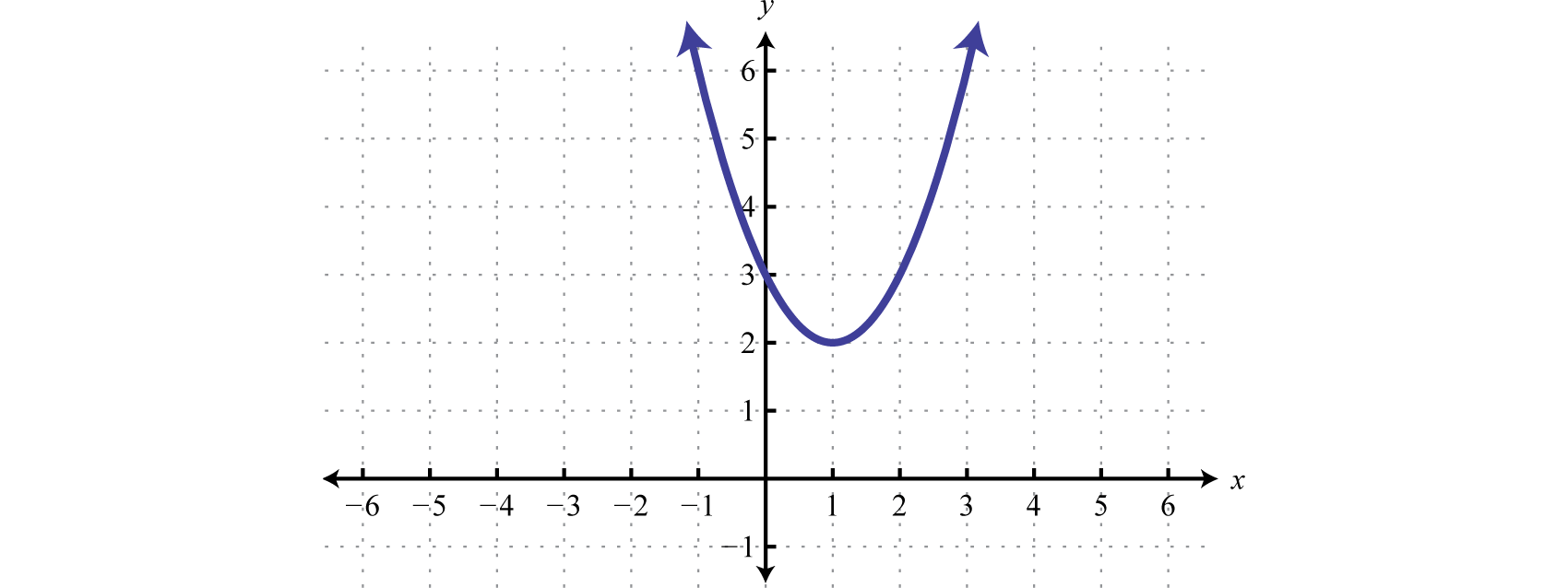
Ми бачимо, що він не має\(x\) -перехоплює і завжди вище\(x\) -осі (позитивний). Якби питання було вирішувати\(x^{2} − 2x + 3 < 0\), то відповідь не була б рішенням. Функція ніколи не буває негативною.
Вправа\(\PageIndex{3}\)
Вирішити:\(9 x^{2}-12 x+4 \leq 0\)
- Відповідь
-
Одне рішення,\(\frac{2}{3}\).
www.youtube.com/В/Е7ВВВВВ_ДС
Приклад\(\PageIndex{7}\):
Знайдіть домен:\(f(x)=\sqrt{x^{2}-4}\).
Рішення
Нагадаємо, що аргумент функції квадратного кореня повинен бути невід'ємним. Тому домен складається з усіх дійсних чисел для\(x\) таких, що\(x^{2} − 4\) більше або дорівнює нулю.
\(x^{2}-4 \geq 0\)
Повинно бути зрозуміло, що\(x^{2} − 4 = 0\) має два рішення\(x = ±2\); це критичні значення. Виберіть тестові значення в кожному інтервалі та оцінюйте\(f (x) = x^{2} − 4\).
\(\begin{aligned} f(-3) &=(-3)^{2}-4=9-4=+\\ f(0) &=(0)^{2}-4=0-4=-\\ f(3) &=(3)^{2}-4=9-4=+\end{aligned}\)
Затінення в\(x\) -значеннях, які дають позитивні результати.

Відповідь:
Домен:\((-\infty,-2] \cup[2, \infty)\)
Ключові винос
- Квадратичні нерівності можуть мати нескінченно багато розв'язків, одне рішення або відсутність рішення.
- Ми можемо розв'язати квадратичні нерівності графічно, спочатку переписуючи нерівність у стандартній формі, з нулем на одній стороні. Графік квадратичної функції і визначте, де вона знаходиться вище або нижче\(x\) -осі. Якщо нерівність передбачає «менше ніж», то визначте\(x\) -значення, де функція знаходиться нижче\(x\) -осі. Якщо нерівність передбачає «більше ніж», то визначте\(x\) -значення, де функція знаходиться над\(x\) віссю -.
- Ми можемо впорядкувати процес розв'язання квадратичних нерівностей, використовуючи знакову діаграму. Діаграма знаків дає нам візуальну довідку, яка вказує, де функція знаходиться над\(x\) осі -за допомогою позитивних знаків або нижче\(x\) -осі за допомогою негативних знаків. Затінення у відповідних значеннях x залежно від вихідної нерівності.
- Щоб скласти діаграму знаків, використовуйте функції та тестові значення в кожному регіоні, обмеженому корінням. Ми стурбовані лише тим, якщо функція позитивна чи негативна, і, таким чином, повний розрахунок не потрібен.
Вправа\(\PageIndex{4}\)
Визначте, чи є дане значення рішенням.
- \(x^{2}-x+1<0 ; x=-1\)
- \(x^{2}+x-1>0 ; x=-2\)
- \(4 x^{2}-12 x+9 \leq 0 ; x=\frac{3}{2}\)
- \(5 x^{2}-8 x-4<0 ; x=-\frac{2}{5}\)
- \(3 x^{2}-x-2 \geq 0 ; x=0\)
- \(4 x^{2}-x+3 \leq 0 ; x=-1\)
- \(2-4 x-x^{2}<0 ; x=\frac{1}{2}\)
- \(5-2 x-x^{2}>0 ; x=0\)
- \(-x^{2}-x-9<0 ; x=-3\)
- \(-x^{2}+x-6 \geq 0 ; x=6\)
- Відповідь
-
1. Ні
3. Так
5. Ні
7. Так
9. Так
Вправа\(\PageIndex{5}\)
Дано графік\(f\) визначення множини розв'язків.
1. \(f(x) \leq 0\);
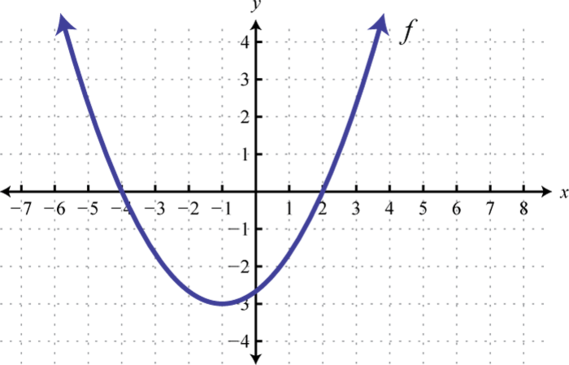
2. \(f(x) \geq 0\);
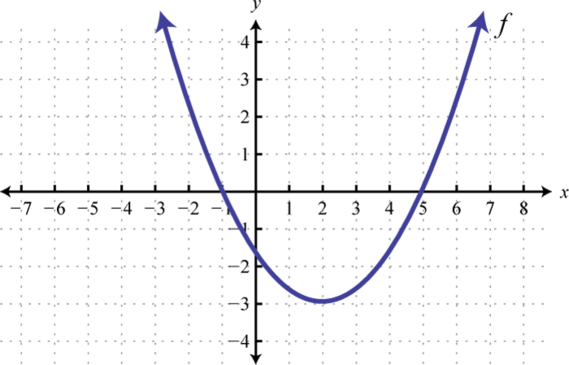
3. \(f(x) \geq 0\);

4. \(f(x) \leq 0\);
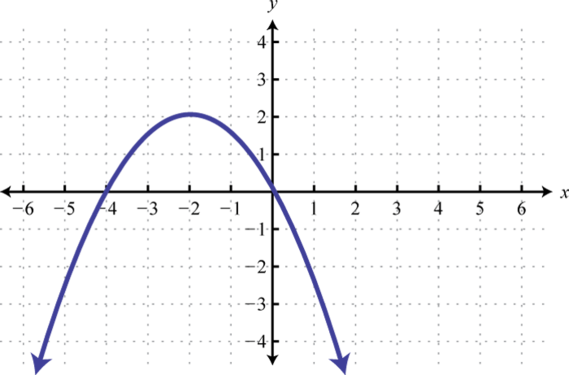
5. \(f(x)>0\);
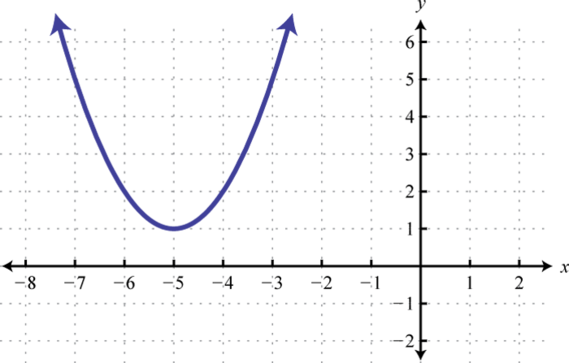
6. \(f(x)<0\);
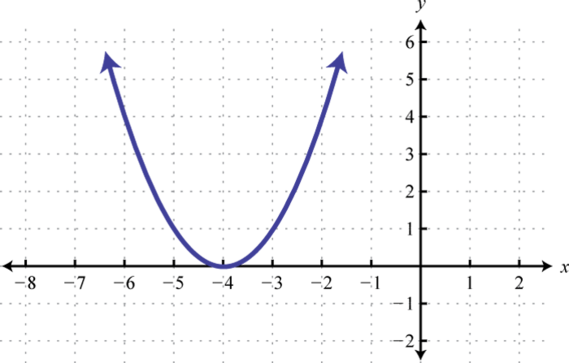
7. \(f(x)>0\);
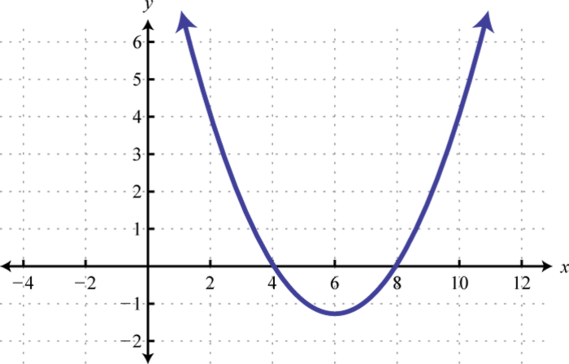
8. \(f(x)<0\);
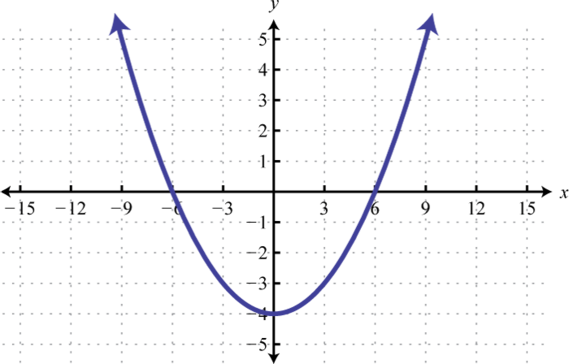
9. \(f(x) \geq 0\);
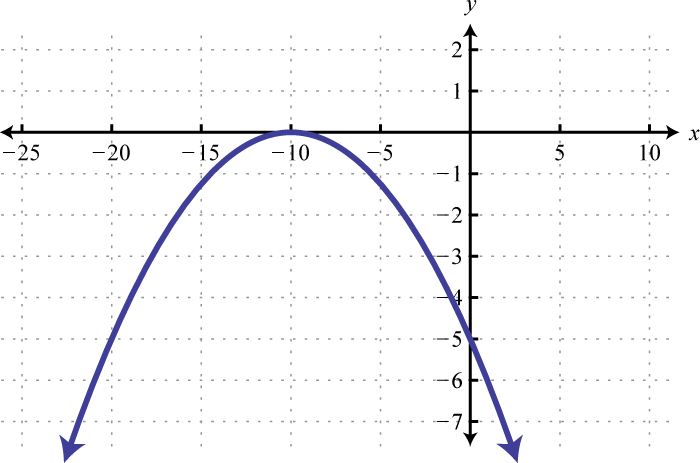
10. \(f(x)<0\);
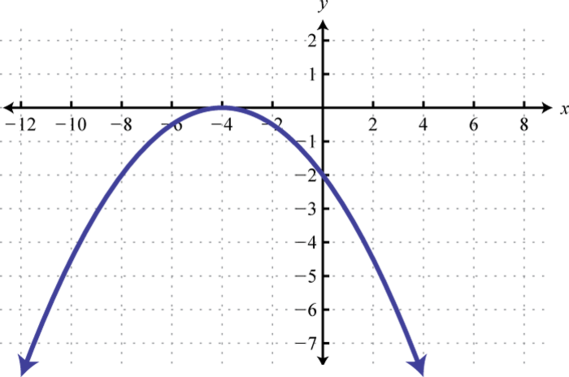
- Відповідь
-
1. \([-4,2]\)
3. \([-1,3]\)
5. \((-\infty, \infty)\)
7. \((-\infty, 4) \cup(8, \infty)\)
9. \(\{-10\}\)
Вправа\(\PageIndex{6}\)
Скористайтеся перетвореннями для побудови графіків, а потім визначте набір розв'язків.
- \(x^{2}-1>0\)
- \(x^{2}+2>0\)
- \((x-1)^{2}>0\)
- \((x+2)^{2} \leq 0\)
- \((x+2)^{2}-1 \leq 0\)
- \((x+3)^{2}-4>0\)
- \(-x^{2}+4 \geq 0\)
- \(-(x+2)^{2}>0\)
- \(-(x+3)^{2}+1<0\)
- \(-(x-4)^{2}+9>0\)
- Відповідь
-
1. \((-\infty,-1) \cup(1, \infty)\)
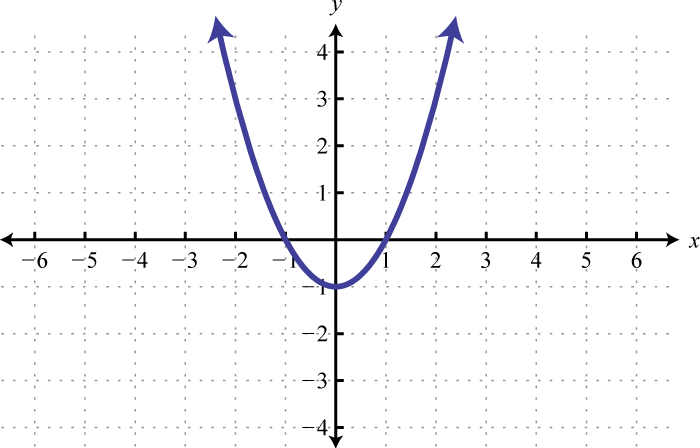
Малюнок\(\PageIndex{30}\) 3. \((-\infty, 1) \cup(1, \infty)\)
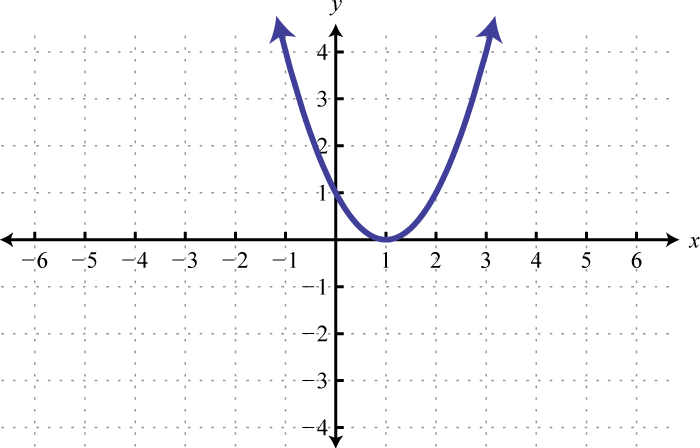
Малюнок\(\PageIndex{31}\) 5. \([-3,-1]\)
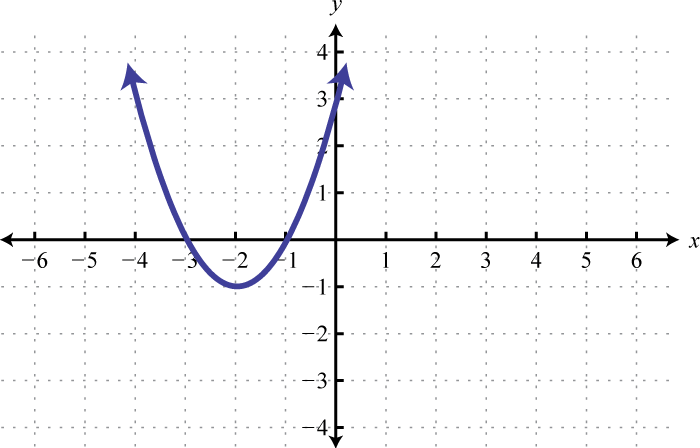
Малюнок\(\PageIndex{32}\) 7. \([-2,2]\)
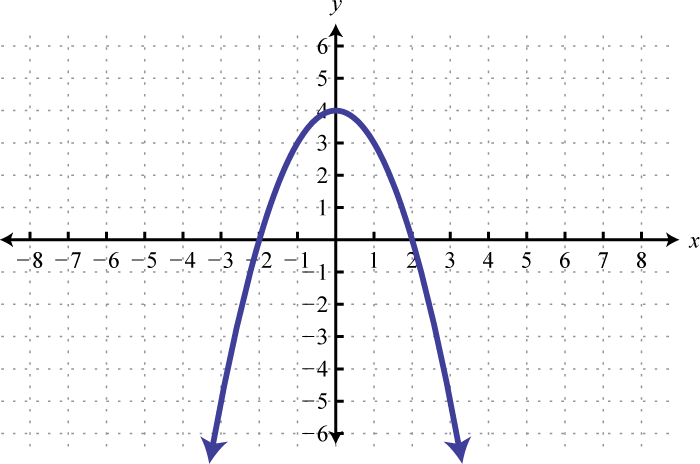
Малюнок\(\PageIndex{33}\) 9. \((-\infty,-4) \cup(-2, \infty)\)
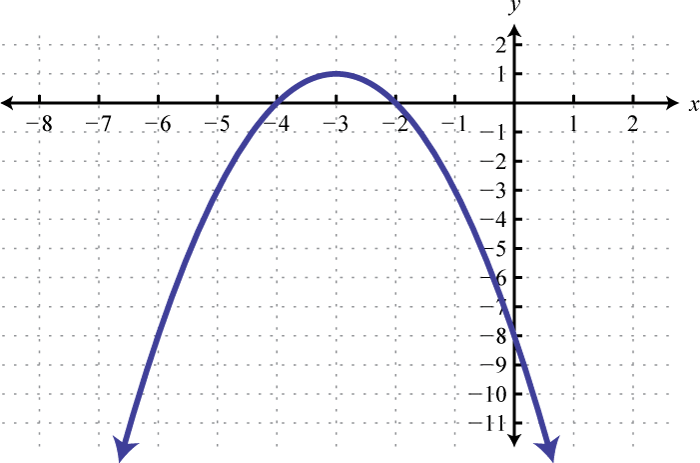
Малюнок\(\PageIndex{34}\)
Вправа\(\PageIndex{7}\)
Використовуйте діаграму знаків для вирішення та графіку набору рішень. Представте відповіді за допомогою інтервальних позначень.
- \(x^{2}-x-12>0\)
- \(x^{2}-10 x+16>0\)
- \(x^{2}+2 x-24<0\)
- \(x^{2}+15 x+54<0\)
- \(x^{2}-23 x-24 \leq 0\)
- \(x^{2}-12 x+20 \leq 0\)
- \(2 x^{2}-11 x-6 \geq 0\)
- \(3 x^{2}+17 x-6 \geq 0\)
- \(8 x^{2}-18 x-5<0\)
- \(10 x^{2}+17 x+6>0\)
- \(9 x^{2}+30 x+25 \leq 0\)
- \(16 x^{2}-40 x+25 \leq 0\)
- \(4 x^{2}-4 x+1>0\)
- \(9 x^{2}+12 x+4>0\)
- \(-x^{2}-x+30 \geq 0\)
- \(-x^{2}-6 x+27 \leq 0\)
- \(x^{2}-64<0\)
- \(x^{2}-81 \geq 0\)
- \(4 x^{2}-9 \geq 0\)
- \(16 x^{2}-25<0\)
- \(25-4 x^{2} \geq 0\)
- \(1-49 x^{2}<0\)
- \(x^{2}-8>0\)
- \(x^{2}-75 \leq 0\)
- \(2 x^{2}+1>0\)
- \(4 x^{2}+3<0\)
- \(x-x^{2}>0\)
- \(3 x-x^{2} \leq 0\)
- \(x^{2}-x+1<0\)
- \(x^{2}+x-1>0\)
- \(4 x^{2}-12 x+9 \leq 0\)
- \(5 x^{2}-8 x-4<0\)
- \(3 x^{2}-x-2 \geq 0\)
- \(4 x^{2}-x+3 \leq 0\)
- \(2-4 x-x^{2}<0\)
- \(5-2 x-x^{2}>0\)
- \(-x^{2}-x-9<0\)
- \(-x^{2}+x-6 \geq 0\)
- \(-2 x^{2}+4 x-1 \geq 0\)
- \(-3 x^{2}-x+1 \leq 0\)
- Відповідь
-
1. \((-\infty,-3) \cup(4, \infty)\)
3. \((-6,4)\)
5. \([-1,24]\)
7. \(\left(-\infty,-\frac{1}{2}\right] \cup[6, \infty)\)
9. \(\left(-\frac{1}{4}, \frac{5}{2}\right)\)
11. \(-\frac{5}{3}\)
13. \(\left(-\infty, \frac{1}{2}\right) \cup\left(\frac{1}{2}, \infty\right)\)
15. \([-6,5]\)
17. \((-8,8)\)
19. \(\left(-\infty,-\frac{3}{2}\right] \cup\left[\frac{3}{2}, \infty\right)\)
21. \(\left[-\frac{5}{2}, \frac{5}{2}\right]\)
23. \((-\infty,-2 \sqrt{2}) \cup(2 \sqrt{2}, \infty)\)
25. \((-\infty, \infty)\)
27. \((0,1)\)
29. \(\emptyset\)
31. \(\frac{3}{2}\)
33. \(\left(-\infty,-\frac{2}{3}\right] \cup[1, \infty)\)
35. \((-\infty,-2-\sqrt{6}) \cup(-2+\sqrt{6}, \infty)\)
37. \((-\infty, \infty)\)
39. \(\left[\frac{2-\sqrt{2}}{2}, \frac{2+\sqrt{2}}{2}\right]\)
Вправа\(\PageIndex{8}\)
Знайдіть домен функції.
- \(f(x)=\sqrt{x^{2}-25}\)
- \(f(x)=\sqrt{x^{2}+3 x}\)
- \(g(x)=\sqrt{3 x^{2}-x-2}\)
- \(g(x)=\sqrt{12 x^{2}-9 x-3}\)
- \(h(x)=\sqrt{16-x^{2}}\)
- \(h(x)=\sqrt{3-2 x-x^{2}}\)
- \(f(x)=\sqrt{x^{2}+10}\)
- \(f(x)=\sqrt{9+x^{2}}\)
- Компанія з виробництва робототехніки визначила, що її щотижневий прибуток у тисячах доларів моделюється тим,\(P (n) = −n^{2} + 30n − 200\) де\(n\) представляє кількість одиниць, які вона виробляє та продає. Скільки одиниць компанія повинна виробляти і продавати для підтримки прибутковості. (Підказка: Прибутковість виникає, коли прибуток перевищує нуль.)
- Висота в ногах снаряда, пострілу прямо в повітря, задається тим,\(h (t) = −16t^{2} + 400t\) де\(t\) представляє час у секундах після його вистрілу. В які часові проміжки знаходиться снаряд під\(1,000\) ногами? Округлити до найближчої десятої частки секунди.
- Відповідь
-
1. \((-\infty,-5] \cup[5, \infty)\)
3. \(\left(-\infty,-\frac{2}{3}\right] \cup[1, \infty)\)
5. \([-4,4]\)
7. \((-\infty, \infty)\)
9. Компанія повинна виробляти і продавати більше\(10\) одиниць і менше\(20\) одиниць щотижня.
Вправа\(\PageIndex{9}\)
- Чи завжди чергується таблиця знаків для будь-якої заданої квадратичної функції? Поясніть і проілюструйте свою відповідь деякими прикладами.
- Досліджуйте та обговоріть інші методи розв'язання квадратичної нерівності.
- Поясніть різницю між квадратним рівнянням і квадратичною нерівністю. Як ми можемо визначити і вирішити кожен? Яка геометрична інтерпретація кожного?
- Відповідь
-
1. Відповідь може відрізнятися
3. Відповідь може відрізнятися
Виноски
15 Математичне твердження, яке пов'язує квадратичний вираз як менший або більший за інший.
16 Значення в області функції, що розділяють області, які дають позитивні або негативні результати.
17 Модель функції з використанням числового рядка і знаків\((+\) або\(−)\) для позначення областей в області, де функція позитивна або негативна.
