2.7: Розв'язування нерівностей з двома змінними
- Page ID
- 58332
Цілі навчання
- Визначте та перевіряйте рішення нерівностей за допомогою двох змінних.
- Графік розв'язку множин лінійних нерівностей з двома змінними.
Розв'язки нерівностей з двома змінними
Ми знаємо, що лінійне рівняння з двома змінними має нескінченно багато впорядкованих парних рішень, які утворюють лінію при графіку. Лінійна нерівність з двома змінними 65, з іншого боку, має набір розв'язків, що складається з області, яка визначає половину площини.
| Лінійне рівняння | Лінійна нерівність |
|---|---|
| \(y = \frac { 3 } { 2 } x + 3\) | \(y \leq \frac { 3 } { 2 } x + 3\) |
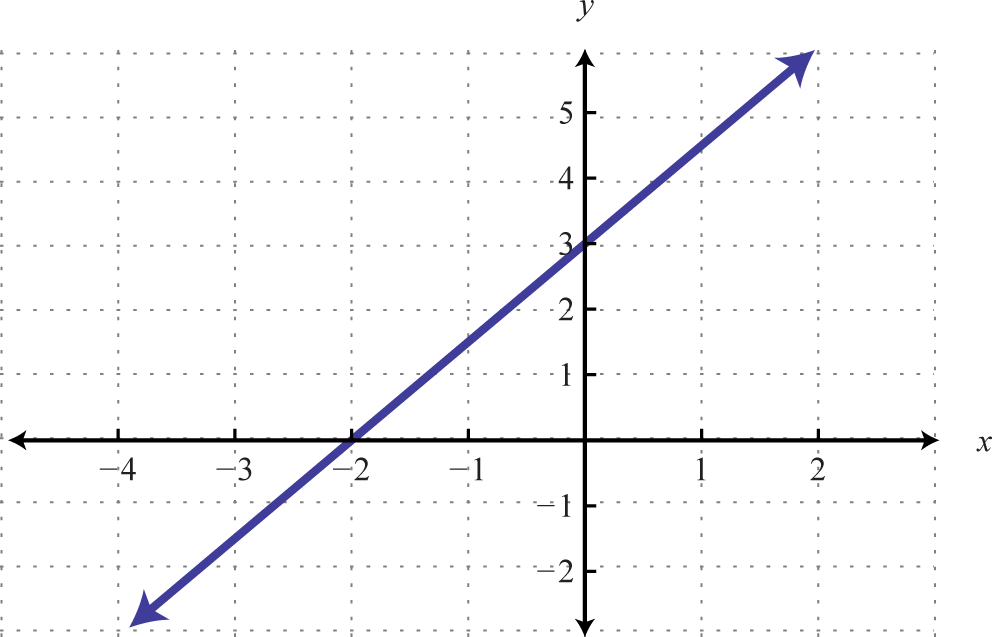 |
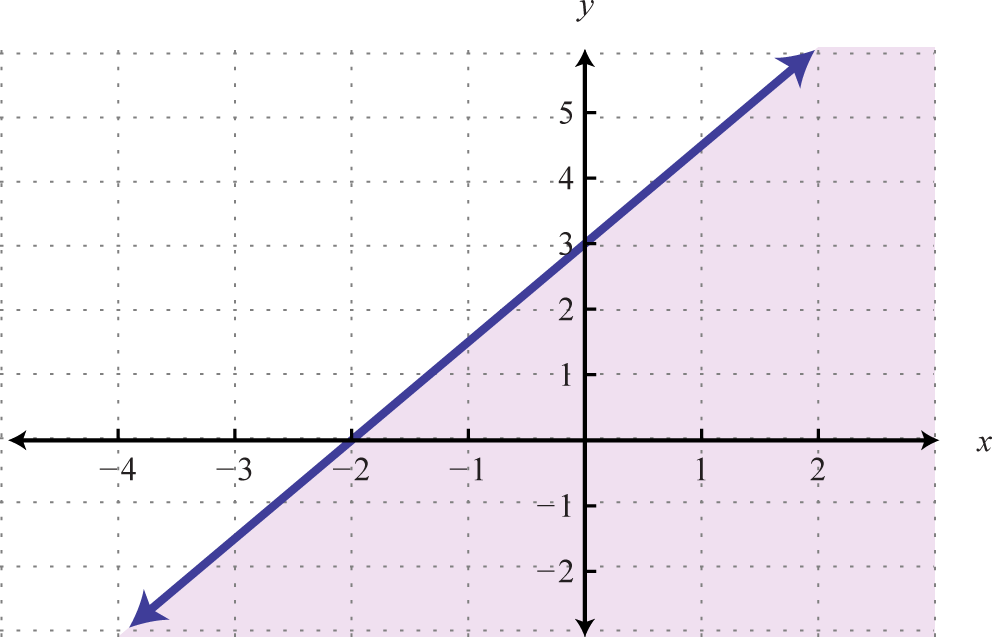 |
Для нерівності лінія визначає межу області, яка затінюється. Це вказує на те, що будь-яка впорядкована пара в затіненій області, включаючи лінію кордону, задовольнить нерівність. Щоб побачити, що це так, виберіть кілька контрольних точок 66 і підставляйте їх у нерівність.
| Тестова точка | \(y \leq \frac { 3 } { 2 } x + 3\) |
| \(( 0,0 )\) | \(\begin{array} { l } { 0 \leq \frac { 3 } { 2 } ( 0 ) + 3 } \\ { 0 \leq 3 } \:\:\:\color{Cerulean}{✓} \end{array}\) |
| \(( 2,1 )\) | \(\begin{array} { l } { 1 \leq \frac { 3 } { 2 } ( 2 ) + 3 } \\ { 1 \leq 3 + 3 } \\ { 1 \leq 6 }\:\:\:\color{Cerulean}{✓} \end{array}\) |
| \(( - 2 , - 1 )\) | \(\begin{array} { l } { - 1 \leq \frac { 3 } { 2 } ( - 2 ) + 3 } \\ { - 1 \leq - 3 + 3 } \\ { - 1 \leq 0 } \:\:\:\color{Cerulean}{✓} \end{array}\) |
Крім того, ми бачимо, що впорядковані пари за межами затіненої області не вирішують лінійну нерівність.
| Тестова точка | \(y \leq \frac { 3 } { 2 } x + 3\) |
| \((-2,3)\) | \ (\ begin {масив} {l} {3\ leq\ frac {3} {2} (- 2) + 3}\\ {3\ leq - 3 + 3}\\ {3\ leq 0\ quad x}\ колір {червоний} {✗}\ кінець {масив}\ |
Графік розв'язку, встановленого на лінійну нерівність, завжди є областю. Однак межа не завжди може бути включена в цей набір. У попередньому прикладі рядок був частиною набору розв'язків через «або дорівнює» частини інклюзивної нерівності\(≤\). Якщо задано сувору нерівність\(<\), ми використаємо пунктирну лінію, щоб вказати, що ці точки не включені до набору розв'язків.
| Межа без включення | Інклюзивна межа |
|---|---|
| \(y < \frac { 3 } { 2 } x + 3\) | \(y \leq \frac { 3 } { 2 } x + 3\) |
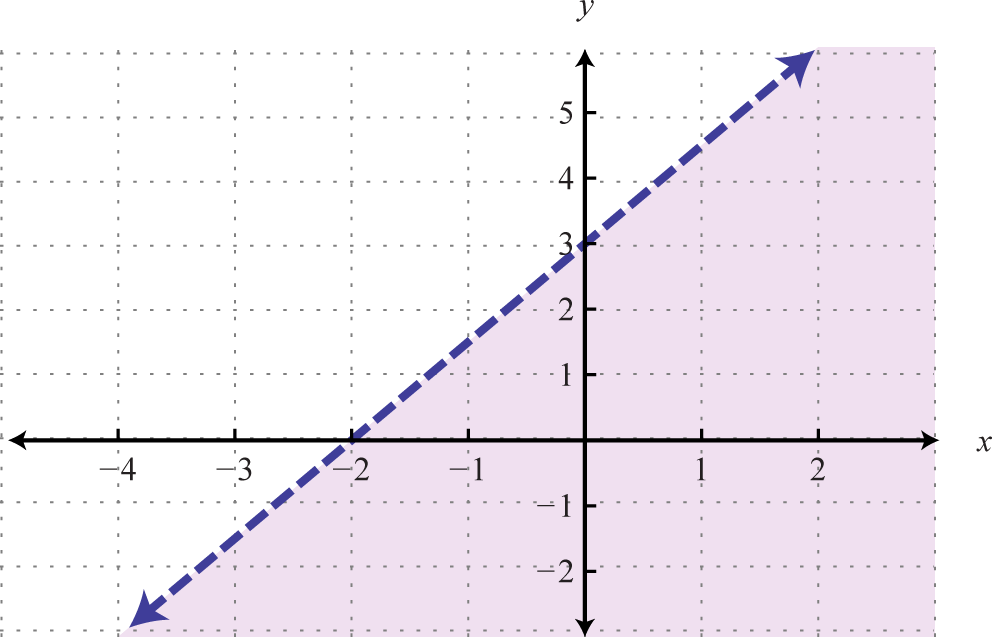 |
 |
Розглянемо точку\((0, 3)\) на кордоні; ця впорядкована пара задовольняє лінійному рівнянню. Саме «або дорівнює» частина інклюзивної нерівності, яка робить впорядковану пару частиною множини розв'язків.
| \(y < \frac { 3 } { 2 } x + 3\) | \(y \leq \frac { 3 } { 2 } x + 3\) |
| \(\begin{array} { l } { 3 < \frac { 3 } { 2 } ( 0 ) + 3 } \\ { 3 < 0 + 3 } \\ { 3 < 3 x } \color{red}{✗}\end{array}\) | \(\begin{array} { l } { 3 \leq \frac { 3 } { 2 } ( 0 ) + 3 } \\ { 3 \leq 0 + 3 } \\ { 3 \leq 3 }\color{Cerulean}{✓} \end{array}\) |
Поки ми бачили приклади нерівностей, які були «менше». Тепер розглянемо наступні графіки з однаковою межею:
| Більше ніж (вище) | Менше ніж (нижче) |
|---|---|
| \(y \geq \frac { 3 } { 2 } x + 3\) | \(y \leq \frac { 3 } { 2 } x + 3\) |
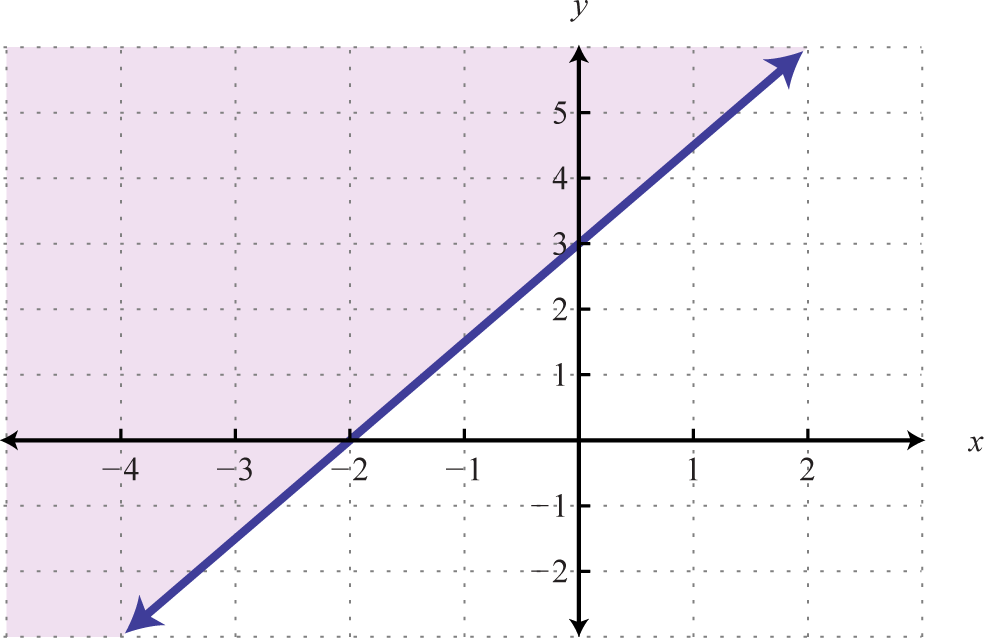 |
 |
Враховуючи наведені вище графіки, що ми можемо очікувати, якщо ми використовуємо походження (0, 0) як тестову точку?
| \(y \geq \frac { 3 } { 2 } x + 3\) | \(y \leq \frac { 3 } { 2 } x + 3\) |
| \(\begin{array} { l } { 0 \geq \frac { 3 } { 2 } ( 0 ) + 3 } \\ { 0 \geq 0 + 3 } \\ { 0 \geq 3 } \color{red}{✗} \end{array}\) | \(\begin{array} { l } { 0 \leq \frac { 3 } { 2 } ( 0 ) + 3 } \\ { 0 \leq 0 + 3 } \\ { 0 \leq 3 } \color{Cerulean}{✓} \end{array}\) |
Приклад\(\PageIndex{1}\):
Визначте, чи\((2, \frac{1}{2})\) є рішенням для\(5x − 2y < 10\).
Рішення
Підставте\(y\) значення\(x\) - і -в рівняння і подивіться, чи буде отримано істинне твердження.
\(\begin{array} { r } { 5 x - 2 y < 10 } \\ { 5 ( \color{Cerulean}{2}\color{Black}{ )} - 2 \left( \color{Cerulean}{\frac { 1 } { 2 }} \right) < 10 } \\ { 10 - 1 < 10 } \\ { 9 < 10 } \color{Cerulean}{✓} \end{array}\)
Відповідь:
\((2, \frac{1}{2})\)це рішення.
Ці ідеї та методи поширюються на нелінійні нерівності з двома змінними. Наприклад, всі рішення будуть\(y > x^{2}\) затінені на графіку нижче.
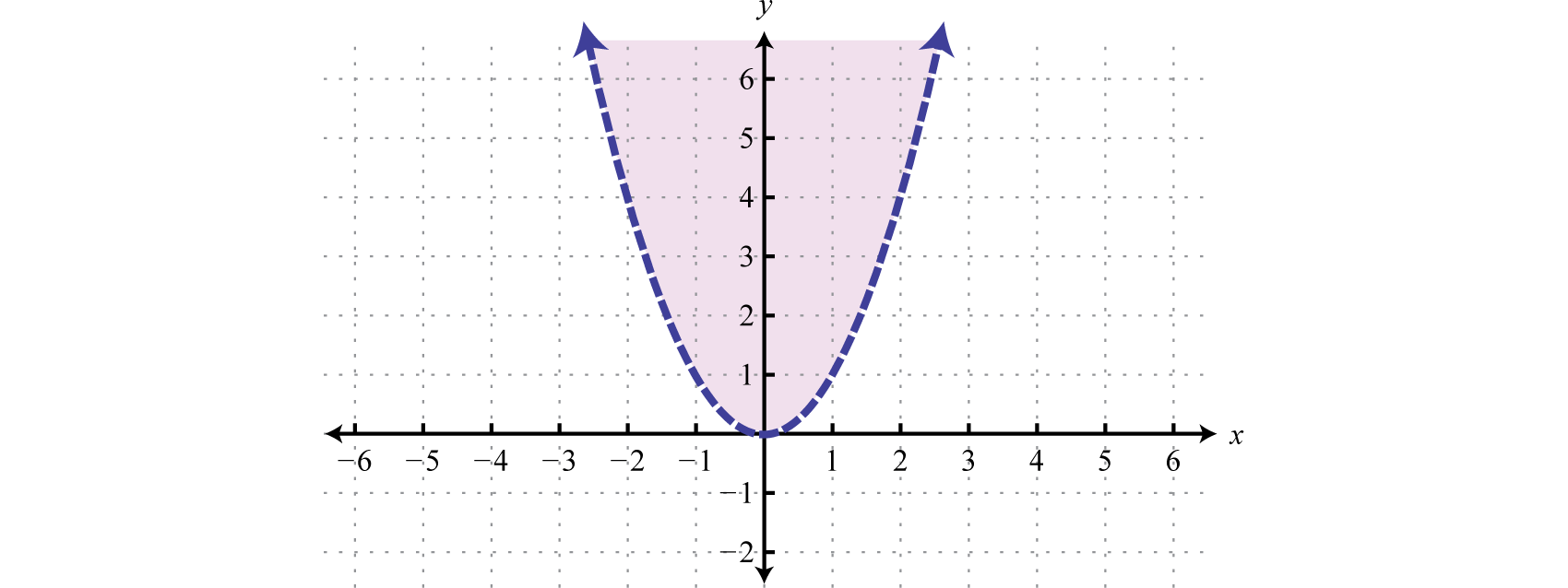
Межа області є параболою, показаною у вигляді пунктирної кривої на графіку, і не є частиною множини розв'язків. Однак з графіка ми очікуємо, що\((−1,4)\) впорядкована пара буде рішенням. Крім того, ми очікуємо, що впорядковані пари, які не знаходяться в затіненій області\((−3, 2)\), наприклад, не задовольнять нерівність.
| Перевірити\((-1, 4)\) | Перевірити\((-3, 2)\) |
| \(\begin{array} { l } { y > x ^ { 2 } } \\ { 4 > ( - 1 ) ^ { 2 } } \\ { 4 > 1 } \color{Cerulean}{✓}\end{array}\) | \(\begin{array} { l } { y > x ^ { 2 } } \\ { 2 > ( - 3 ) ^ { 2 } } \\ { 2 > 9 } \color{red}{✗}\end{array}\) |
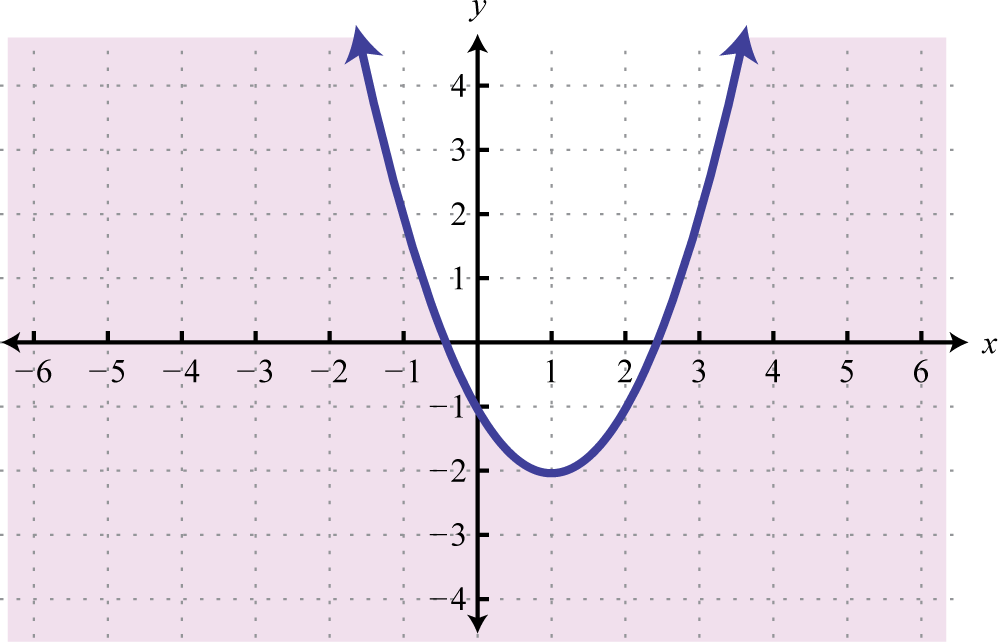
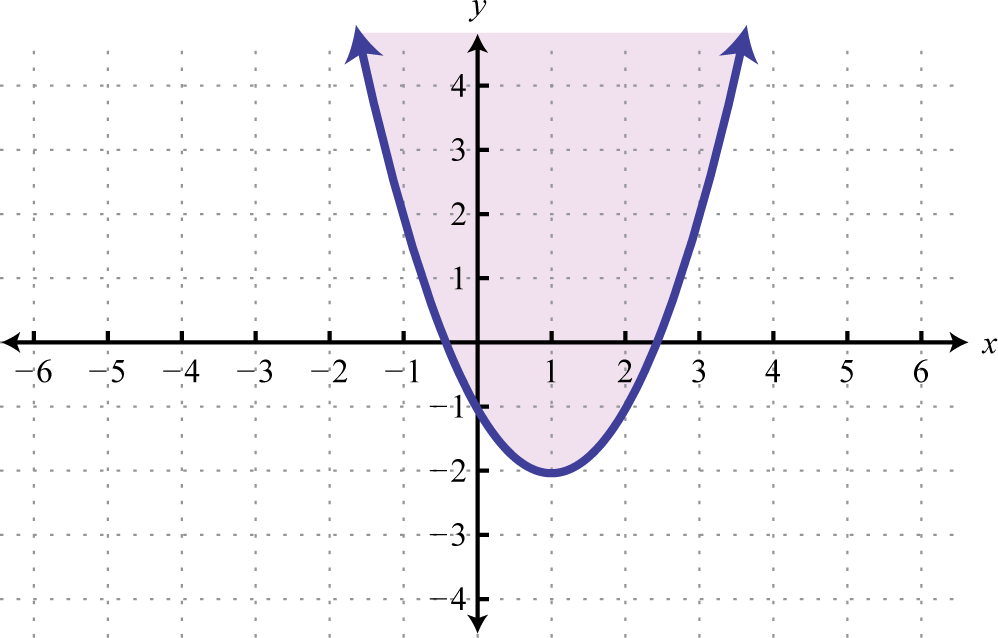
Далі наведено графіки розв'язків множин нерівностей з інклюзивними параболічними межами.
| \(y \leq ( x - 1 ) ^ { 2 } - 2\) | \(y \geq ( x - 1 ) ^ { 2 } - 2\) |
 |
 |
Вам рекомендується перевірити точки в і з кожного набору рішень, який наведений вище.
Вправа\(\PageIndex{1}\)
Чи\((-3, -2)\) є рішенням\(2x-3y<0\)?
- Відповідь
-
Ні
www.youtube.com/В/ІнтудаФЛК
Графічні розв'язки нерівностей з двома змінними
Розв'язки лінійних нерівностей - це затінена напівплощина, обмежена суцільною лінією або пунктирною лінією. Ця межа або включається в розв'язок, або ні, залежно від заданої нерівності. Якщо нам дано сувору нерівність, ми використовуємо пунктирну лінію, щоб вказати, що межа не включена. Якщо нам дано інклюзивну нерівність, ми використовуємо суцільну лінію, щоб вказати, що вона включена. Етапи побудови графіків розв'язку, встановленого для нерівності з двома змінними, наведені в наступному прикладі.
Приклад\(\PageIndex{2}\):
Графік набору розв'язків\(y>−3x+1\).
Рішення
- Крок 1: Графік кордону. Через сувору нерівність ми будемо графувати межу,\(y=−3x+1\) використовуючи пунктирну лінію. Ми бачимо, що нахил є\(m=−3=−\frac{3}{1}=\frac{rise}{run}\) і\(y\) -перехоплення є\((0, 1)\).
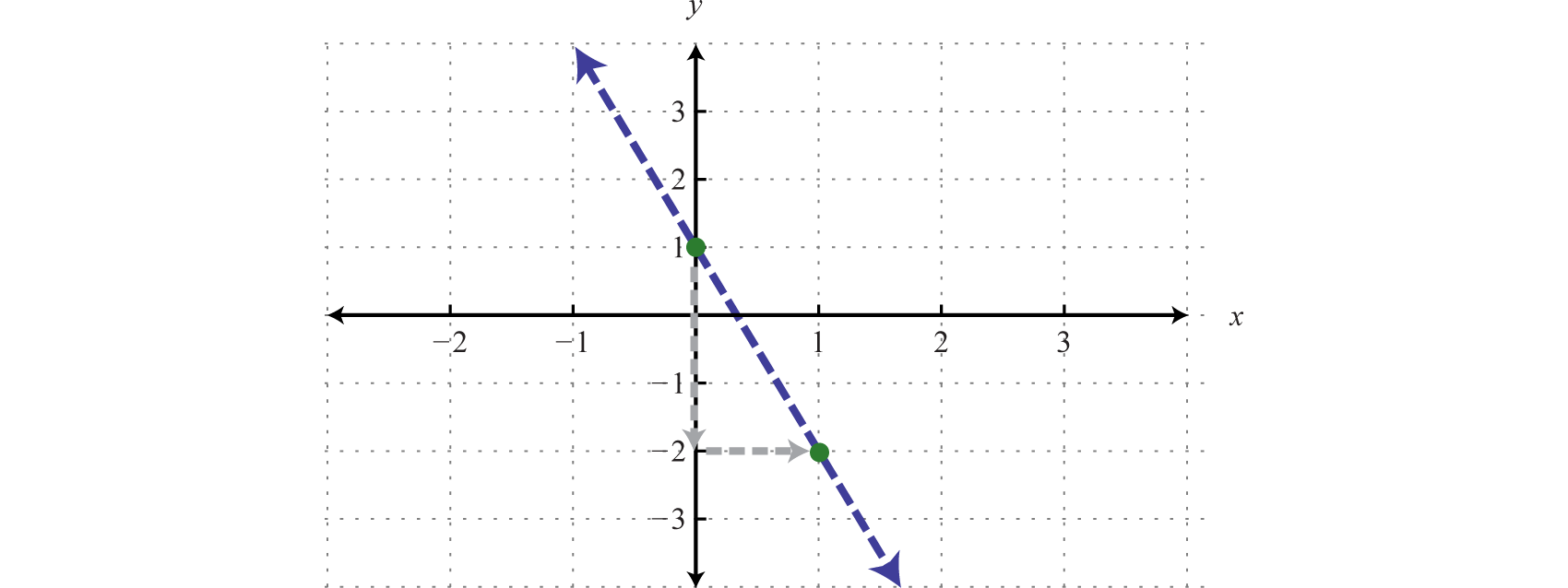
Малюнок\(\PageIndex{10}\)
- Крок 2: Перевірте точку, яка не знаходиться на кордоні. Загальною тестовою точкою є походження,\((0, 0)\). Тестова точка допомагає нам визначити, яку половину площини затінювати.
Таблиця\(\PageIndex{10}\)Тестова точка \(y > - 3 x + 1\) \((0,0)\) \(\begin{array} { l } { 0 > - 3 ( 0 ) + 1 } \\ { 0 > 1 }\color{red}{✗} \end{array}\) - Крок 3: Затіньте область, що містить розчини. Оскільки тестова точка не\((0, 0)\) була рішенням, вона не лежить в регіоні, що містить всі впорядковані парні рішення. Тому затінюйте половину площини, яка не містить цієї тестової точки. В цьому випадку затінюють над лінією кордону.
Відповідь:
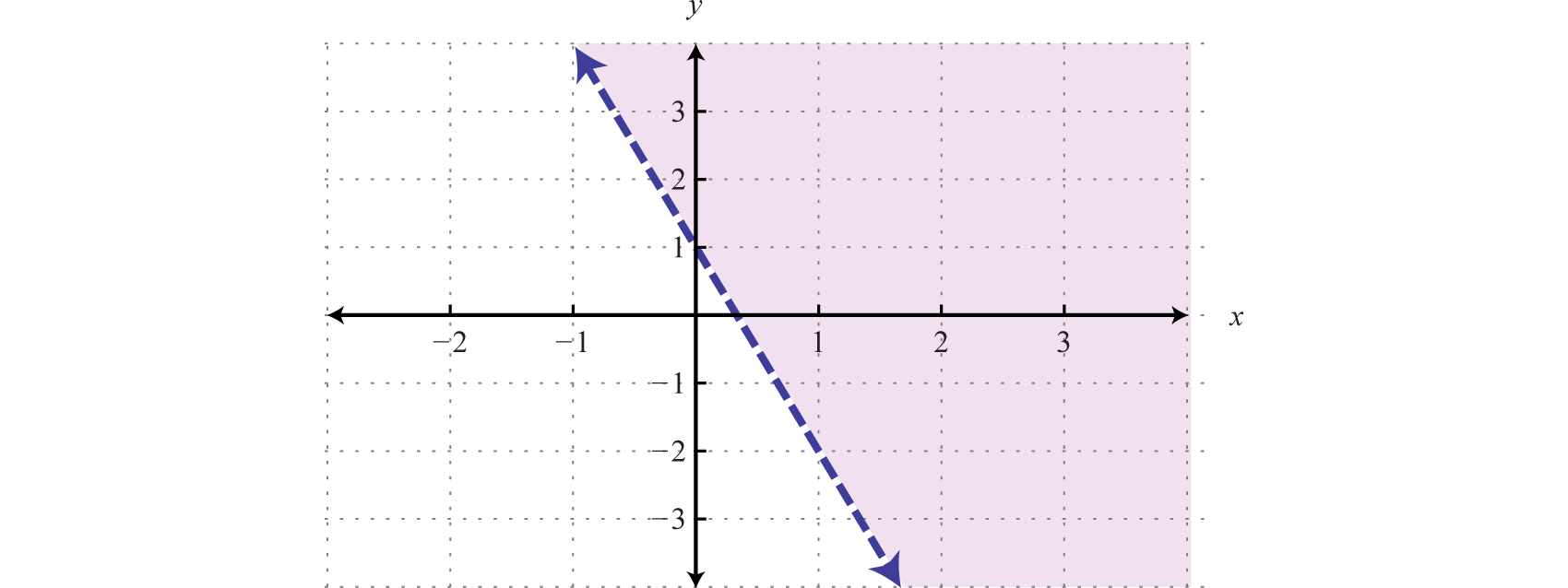
Розглянемо задачу затінення над або нижче лінії кордону, коли нерівність знаходиться в ухилі-перехопленому вигляді. Якщо\(y > mx + b\), то затінюйте над лінією. Якщо\(y < mx + b\), то затінюйте нижче лінії. Розтушовуйте з обережністю; іноді межа дається в стандартному вигляді, в такому випадку ці правила не застосовуються.
Приклад\(\PageIndex{3}\):
Графік набору розв'язків\(2 x - 5 y \geq - 10\).
Рішення
Тут межа визначається лінією\(2x − 5y = −10\). Оскільки нерівність є інклюзивною, графуємо межу за допомогою суцільної лінії. У цьому випадку графуйте лінію кордону за допомогою перехоплень.
| Щоб знайти\(x\) -перехоплення, встановлюємо\(y = 0\). | Щоб знайти\(y\) -перехоплення, встановлюємо\(x = 0\). |
| \(\begin{array} { c } { 2 x - 5 y = - 10 } \\ { 2 x - 5 ( \color{Cerulean}{0}\color{Black}{ )} = - 10 } \\ { 2 x = - 10 } \\ { x = - 5 } \end{array}\) | \(\begin{array} { r } { 2 x - 5 y = - 10 } \\ { 2 ( \color{Cerulean}{0}\color{Black}{ )} - 5 y = - 10 } \\ { - 5 y = - 10 } \\ { y = 2 } \end{array}\) |
| \(x\)-перехоплення:\((−5, 0)\) | \(y\)-перехоплення:\((0, 2)\) |
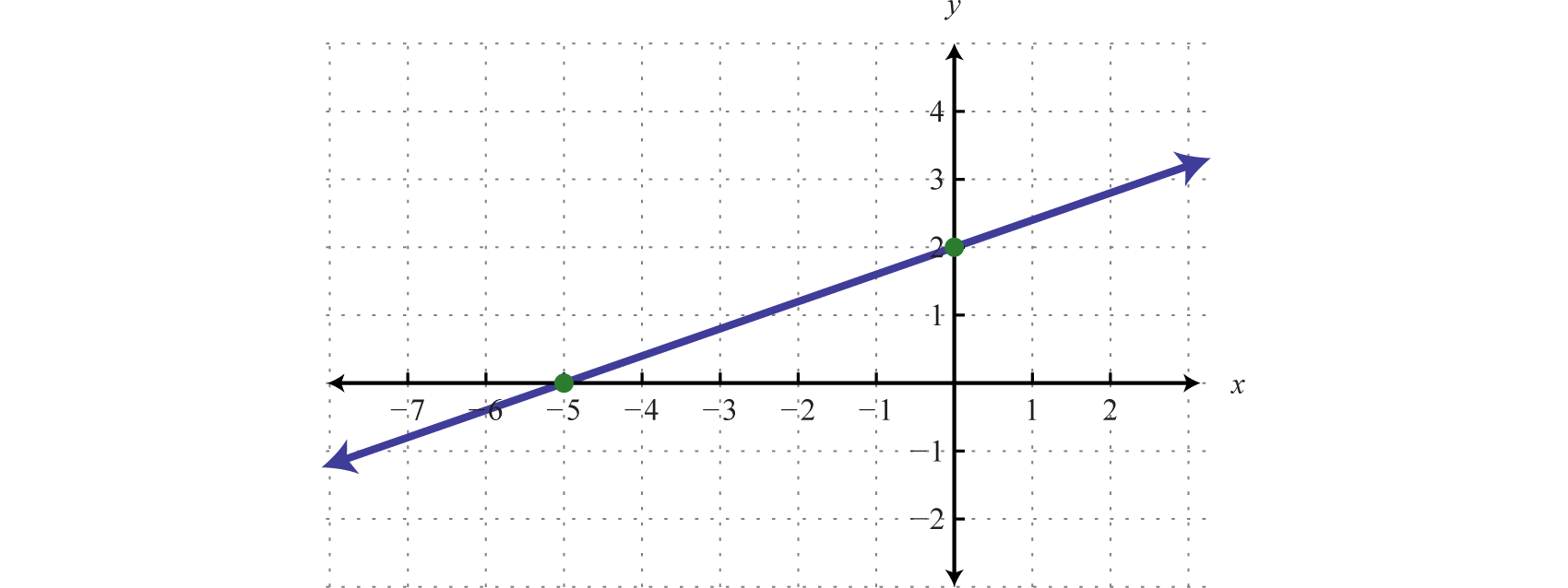
Далі протестуйте точку; це допомагає вирішити, яку область затінювати.
| Тестова точка | \(2 x - 5 y \geq - 10\) |
| \((0,0)\) | \(\begin{aligned} 2 ( 0 ) - 5 ( 0 ) & \geq - 10 \\ 0 & \geq - 10 \color{Cerulean}{✓}\end{aligned}\) |
Оскільки контрольна точка знаходиться в наборі розчину, затіньте половину площини, яка її містить.
Відповідь:
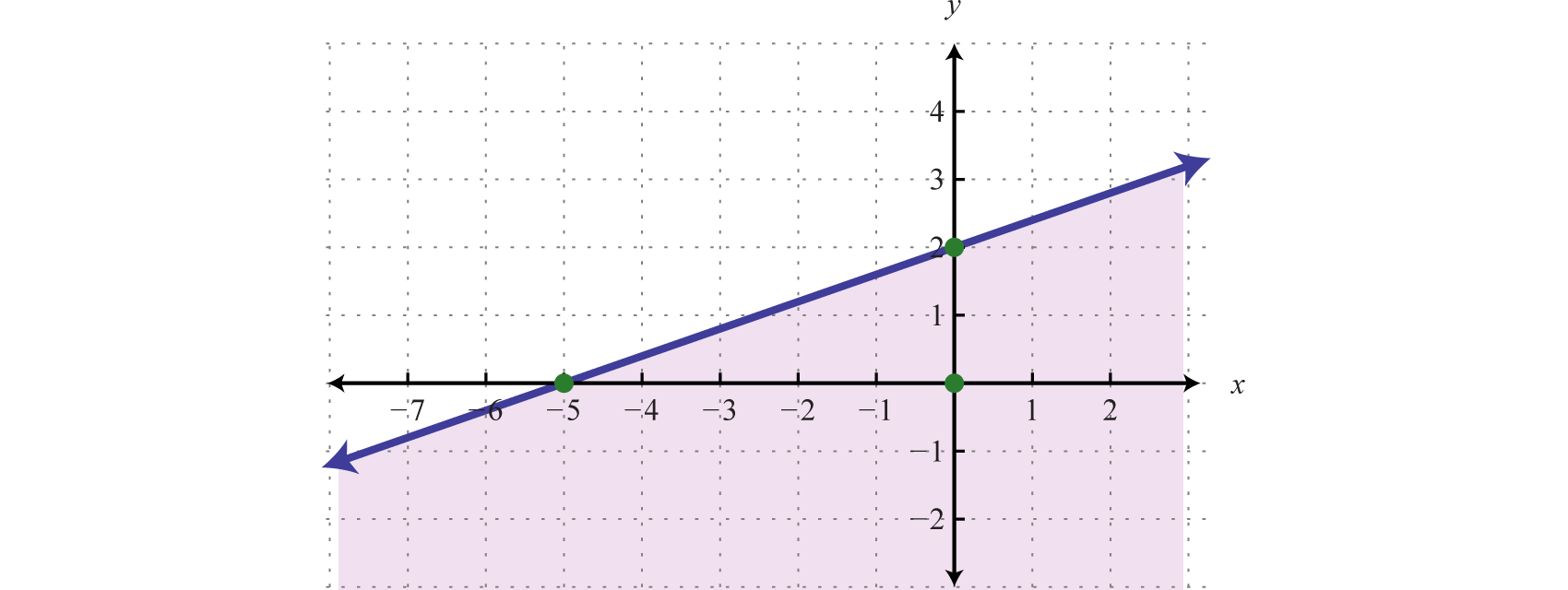
У цьому прикладі зверніть увагу, що набір розв'язків складається з усіх впорядкованих пар, розташованих нижче лінії кордону. Це може здатися контрінтуїтивним, оскільки початкова нерівність включала «більше, ніж»\(≥\). Це ілюструє, що це найкраща практика, щоб насправді перевірити точку. Вирішіть для,\(y\) і ви побачите, що затінення правильне.
\(\begin{aligned} 2 x - 5 y & \geq - 10 \\ 2 x - 5 y \color{Cerulean}{- 2 x} & \geq - 10 \color{Cerulean}{-2x} \\ - 5 y & \geq - 2 x - 10 \\ \frac { - 5 y } { \color{Cerulean}{- 5} } & \color{OliveGreen}{\leq} \color{Black}{\frac { - 2 x - 10 } { \color{Cerulean}{- 5} }} \:\:\:\color{Cerulean}{Reverse\: the\: inequality.}\\ y & \leq \frac { 2 } { 5 } x + 2 \end{aligned}\)
У формі нахилу-перехоплення можна побачити, що область нижче лінії кордону повинна бути затінена. Альтернативний підхід полягає в тому, щоб спочатку висловити межу у формі перехоплення нахилу, намалювати її, а потім затінювати відповідну область.
Приклад\(\PageIndex{4}\):
Графік набору розв'язків\(y <2\).
Рішення
Спочатку графуйте лінію кордону\(y = 2\) пунктирною лінією через сувору нерівність. Далі протестуйте точку.
| Тестова точка | \(y<2\) |
| \((0,0)\) | \(0 < 2\color{Cerulean}{✓}\) |
В цьому випадку затіньте область, яка містить контрольну точку.
Відповідь:
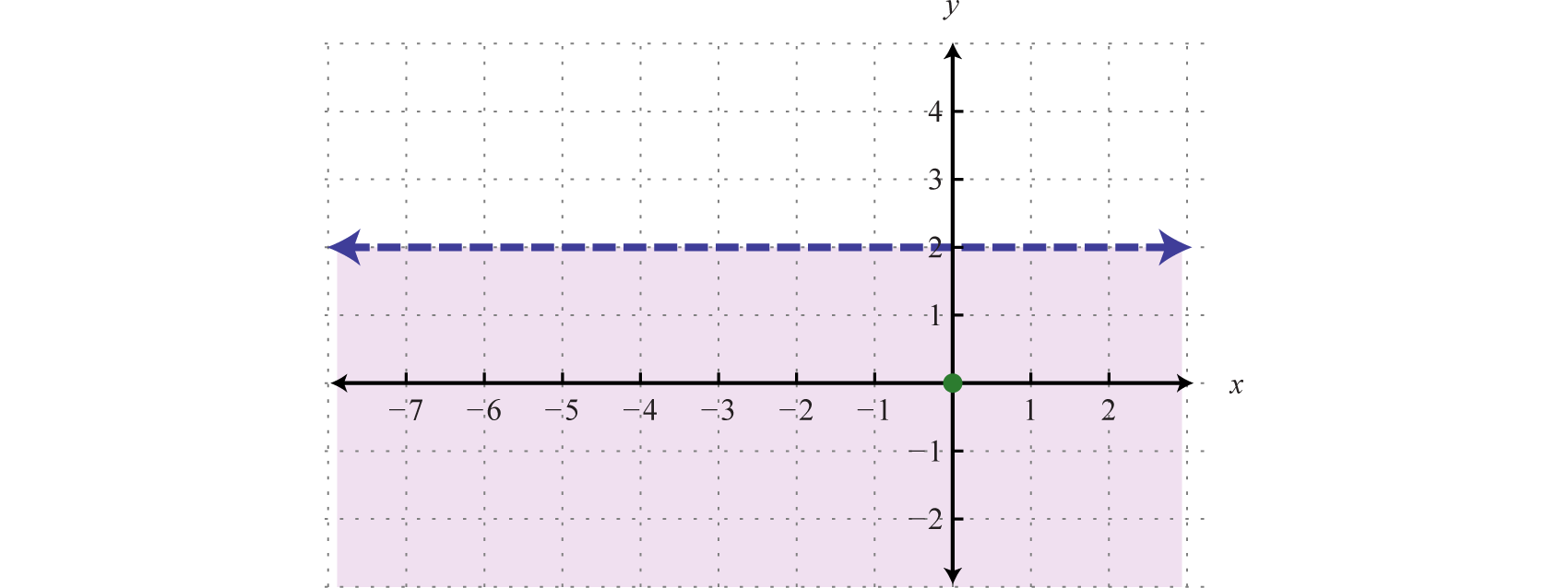
Вправа\(\PageIndex{2}\)
Графік набору розв'язків\(2 x - 3 y < 0\).
- Відповідь
-
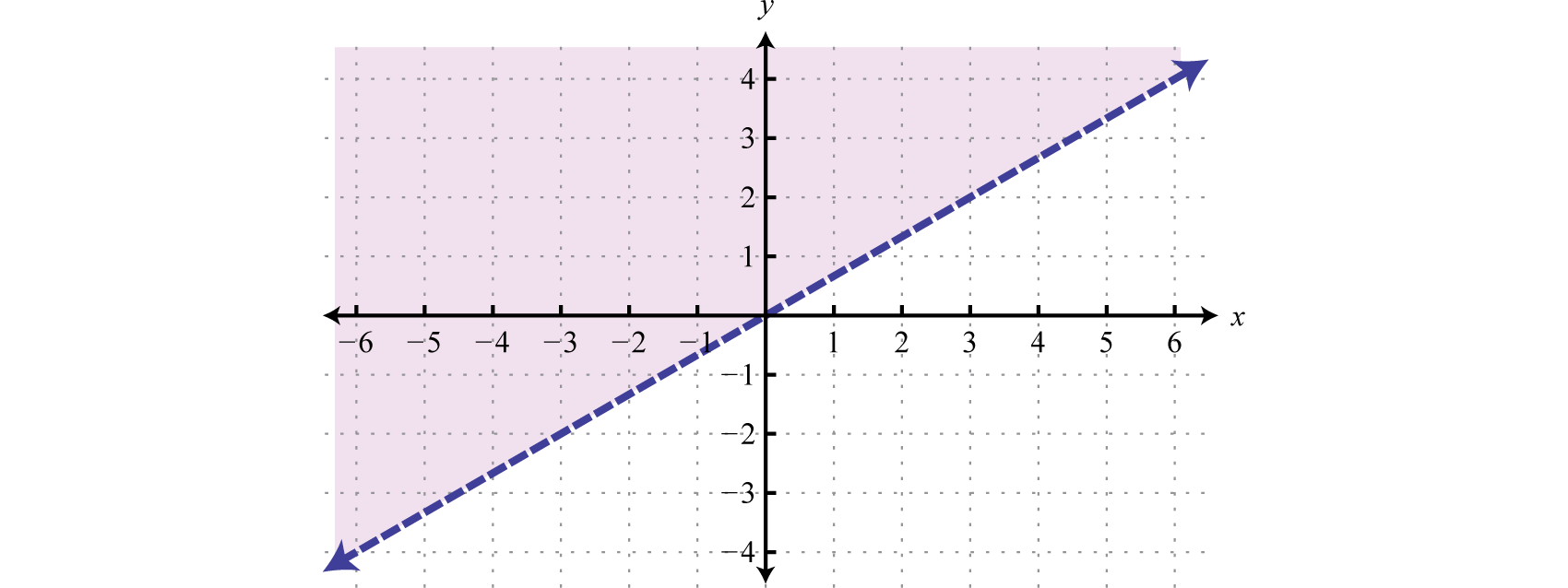
Малюнок\(\PageIndex{15}\) www.youtube.com/В/53ГЛ ФМ7ГК
Етапи однакові для нелінійних нерівностей з двома змінними. Спочатку проведіть графік межі, а потім перевірте точку, щоб визначити, яка область містить розв'язки.
Приклад\(\PageIndex{5}\):
Графік набору розв'язків\(y < ( x + 2 ) ^ { 2 } - 1\).
Рішення
Межа є основною параболою зміщені\(2\) одиниці вліво і\(1\) одиниці вниз. Почніть з малювання пунктирної параболічної межі через сувору нерівність.
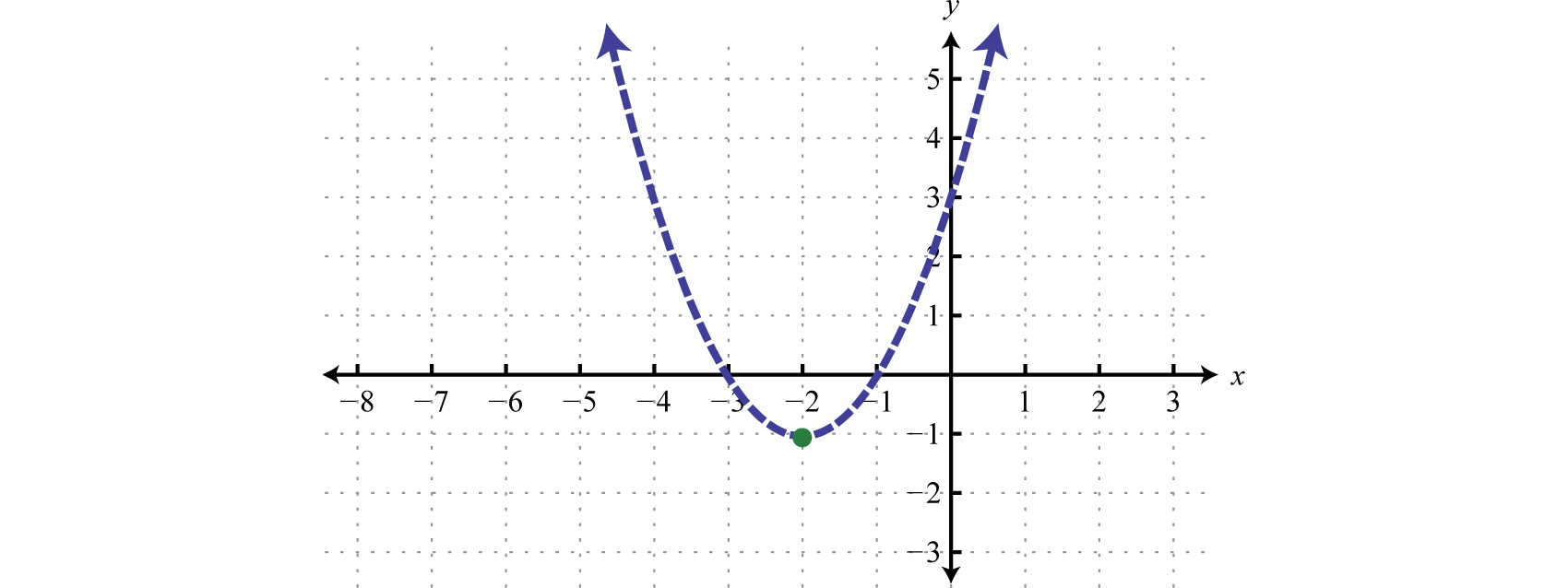
Далі протестуйте точку.
| Тестова точка | \(y < ( x + 2 ) ^ { 2 } - 1\) |
| \((0,0)\) | \(\begin{array} { l } { 0 < ( 0 + 2 ) ^ { 2 } - 1 } \\ { 0 < 4 - 1 } \\ { 0 < 3 } \color{Cerulean}{✓}\end{array}\) |
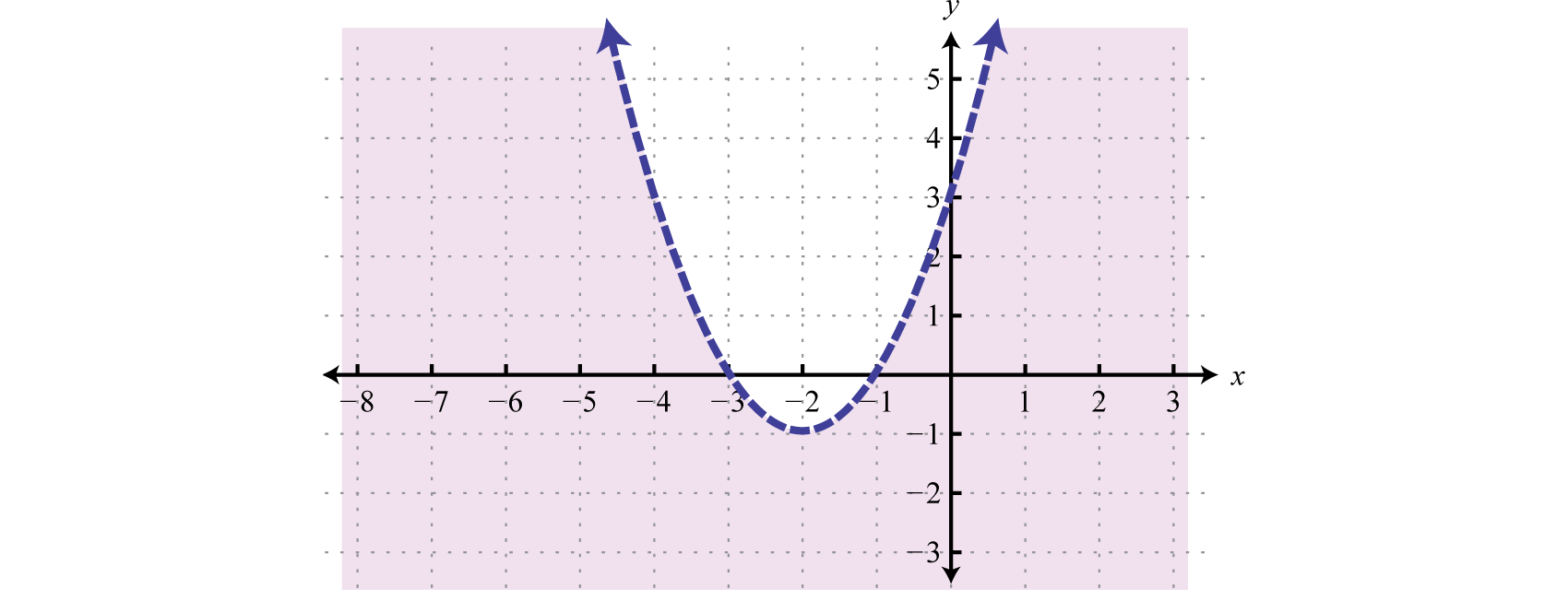
В цьому випадку затіньте область, яка містить контрольну точку\((0, 0)\).
Відповідь:
Приклад\(\PageIndex{6}\):
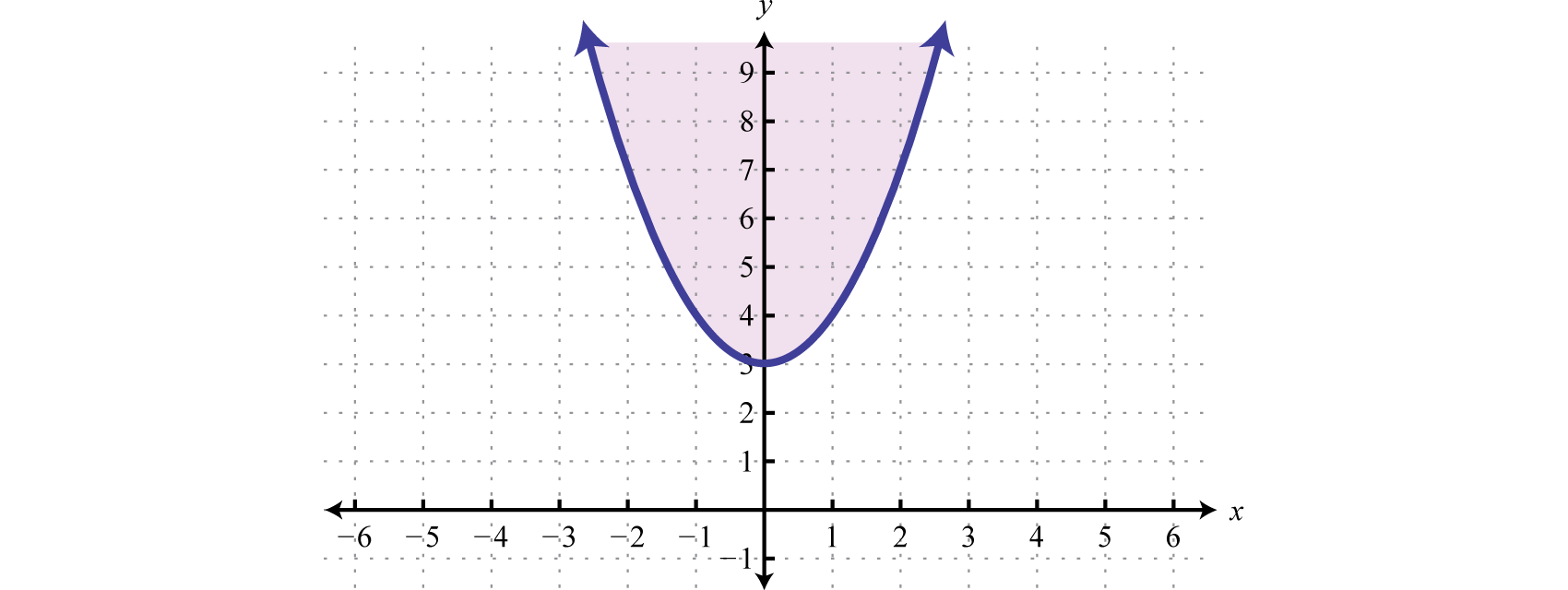
Графік набору розв'язків\(y \geq x ^ { 2 } + 3\).
Рішення
Межа являє собою базову параболу зміщених\(3\) одиниць вгору. Він графікується за допомогою твердої кривої через інклюзивну нерівність.
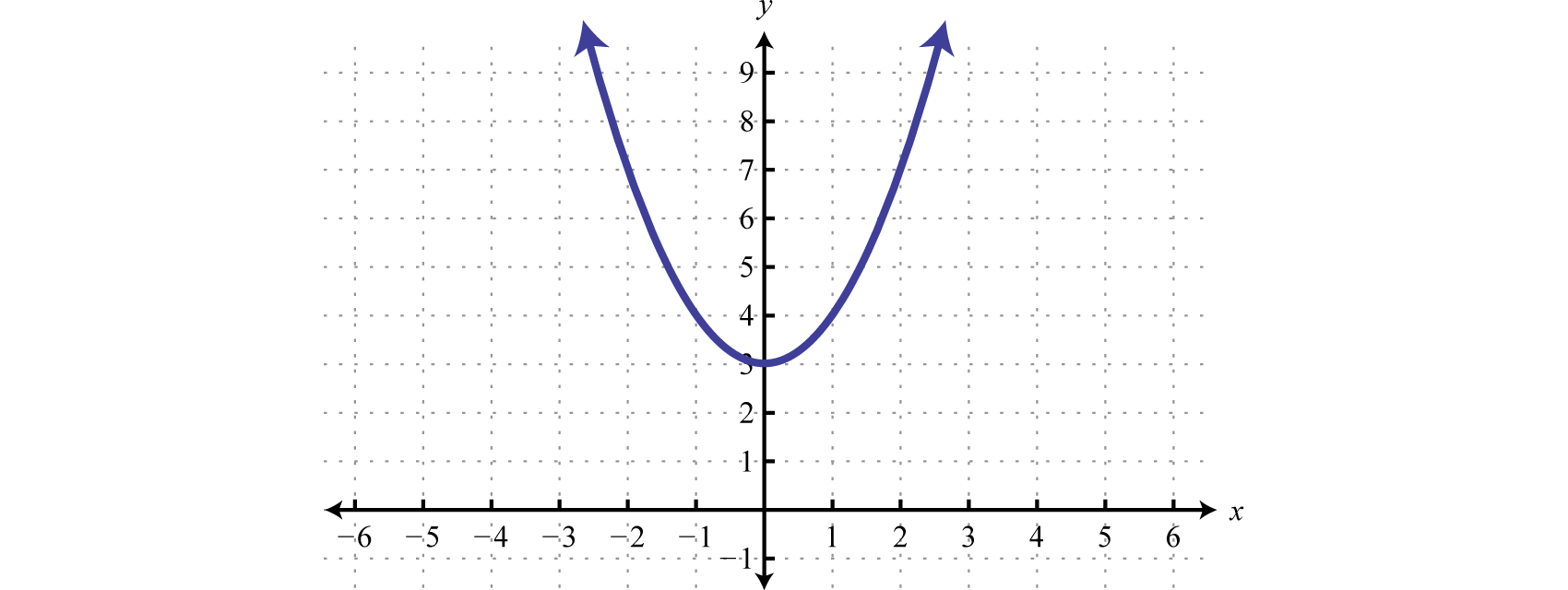
Далі протестуйте точку.
| Тестова точка | \(y \geq x ^ { 2 } + 3\) |
| \((0,0)\) | \(\begin{array} { l } { 0 \geq 0 ^ { 2 } + 3 } \\ { 0 \geq 3 } \color{red}{✗} \end{array}\) |
В цьому випадку затіньте область, яка не містить контрольної точки\((0,0)\).
Відповідь:
Вправа\(\PageIndex{3}\)
Графік набору розв'язків\(y < | x - 1 | - 3\).
- Відповідь
-
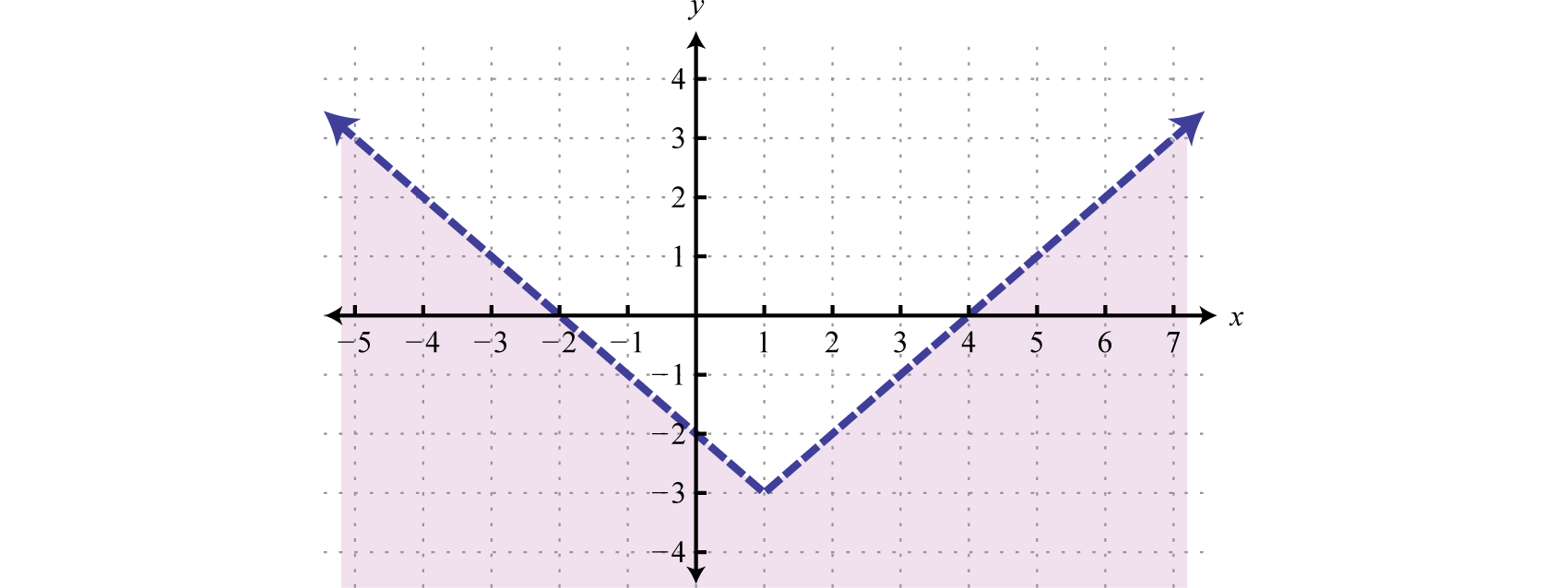
Малюнок\(\PageIndex{20}\) www.youtube.com/В/BVBX_UNVCOS
Ключові винос
- Лінійні нерівності з двома змінними мають нескінченно багато впорядкованих парних розв'язків, які можуть бути побудовані шляхом затінення у відповідній половині прямокутної координатної площини.
- Для графіку множини розв'язку нерівності з двома змінними спочатку графують межу пунктирною або суцільною лінією залежно від нерівності. Якщо задано сувору нерівність, використовуйте пунктирну лінію для кордону. Якщо задано інклюзивну нерівність, використовуйте суцільну лінію. Далі вибираємо контрольну точку не на кордоні. Якщо контрольна точка вирішує нерівність, то затіньте область, яка її містить; інакше затіньте протилежну сторону.
- Перевірте свою відповідь, перевіривши точки в і з області затінення, щоб переконатися, що вони вирішують нерівність чи ні.
Вправа\(\PageIndex{4}\)
Чи є впорядкована пара розв'язком заданої нерівності?
- \(5 x - y > - 2 ; ( - 3 , - 4 )\)
- \(4 x - y < - 8 ; ( - 3 , - 10 )\)
- \(6 x - 15 y \geq - 1 ; \left( \frac { 1 } { 2 } , - \frac { 1 } { 3 } \right)\)
- \(x - 2 y \geq 2 ; \left( \frac { 2 } { 3 } , - \frac { 5 } { 6 } \right)\)
- \(\frac { 3 } { 4 } x - \frac { 2 } { 3 } y < \frac { 3 } { 2 } ; ( 1 , - 1 )\)
- \(\frac { 2 } { 5 } x + \frac { 4 } { 3 } y > \frac { 1 } { 2 } ; ( - 2,1 )\)
- \(y \leq x ^ { 2 } - 1 ; ( - 1,1 )\)
- \(y \geq x ^ { 2 } + 3 ; ( - 2,0 )\)
- \(y \geq ( x - 5 ) ^ { 2 } + 1 ; ( 3,4 )\)
- \(y \leq 2 ( x + 1 ) ^ { 2 } - 3 ; ( - 1 , - 2 )\)
- \(y > 3 - | x | ; ( - 4 , - 3 )\)
- \(y < | x | - 8 ; ( 5 , - 7 )\)
- \(y > | 2 x - 1 | - 3 ; ( - 1,3 )\)
- \(y < | 3 x - 2 | + 2 ; ( - 2,10 )\)
- Відповідь
-
1. Ні
3. Так
5. Так
7. Ні
9. Ні
11. Ні
13. Так
Вправа\(\PageIndex{5}\)
Графік набору розв'язків.
- \(y < 2 x - 1\)
- \(y > −4x + 1\)
- \(y ≥ −\frac{2}{3} x + 3\)
- \(y ≤ \frac{4}{3} x − 3\)
- \(2x + 3y ≤ 18\)
- \(5x + 2y ≤ 8\)
- \(6x − 5y > 30\)
- \(8x − 6y < 24\)
- \(3x − 4y < 0\)
- \(x − 3y > 0\)
- \(x + y ≥ 0\)
- \(x − y ≥ 0\)
- \(y ≤ −2\)
- \(y > −3\)
- \(x < −2\)
- \(x ≥ −3\)
- \(\frac { 1 } { 6 } x + \frac { 1 } { 10 } y \leq \frac { 1 } { 2 }\)
- \(\frac { 3 } { 8 } x + \frac { 1 } { 2 } y \geq \frac { 3 } { 4 }\)
- \(\frac { 1 } { 12 } x - \frac { 1 } { 6 } y < \frac { 2 } { 3 }\)
- \(\frac { 1 } { 3 } x - \frac { 1 } { 9 } y > \frac { 4 } { 3 }\)
- \(5x ≤ −4y − 12\)
- \(−4x ≤ 12 − 3y\)
- \(4y + 2 < 3x\)
- \(8x < 9 − 6y\)
- \(5 ≥ 3x − 15y\)
- \(2 x \geq 6 - 9 y\)
- Напишіть нерівність, яка описує всі точки у верхній півплощині над\(x\) -віссю.
- Напишіть нерівність, яка описує всі точки в нижній півплощині нижче\(x\) -осі.
- Напишіть нерівність, яка описує всі точки на півплощині ліворуч від\(y\) -осі.
- Напишіть нерівність, яка описує всі точки на півплощині праворуч від\(y\) -осі.
- Напишіть нерівність, яка описує всі впорядковані пари,\(y\) -координата яких є принаймні\(k\) одиницями.
- Напишіть нерівність, яка описує всі впорядковані пари, у яких\(x\) -координата становить не більше\(k\) одиниць.
- Відповідь
-
1.
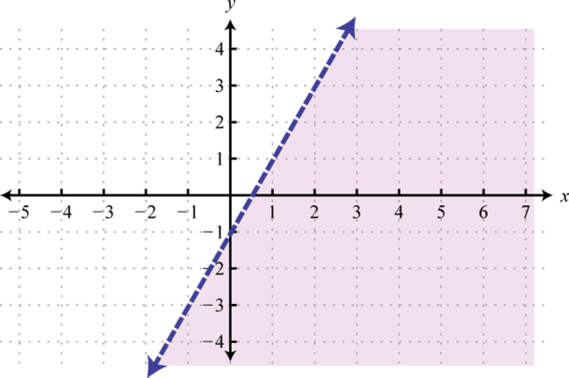
Малюнок\(\PageIndex{21}\) 3.
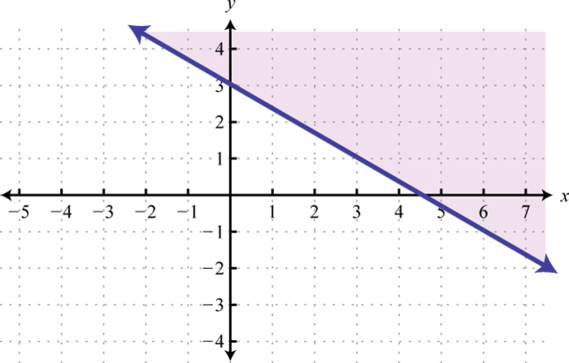
Малюнок\(\PageIndex{22}\) 5.
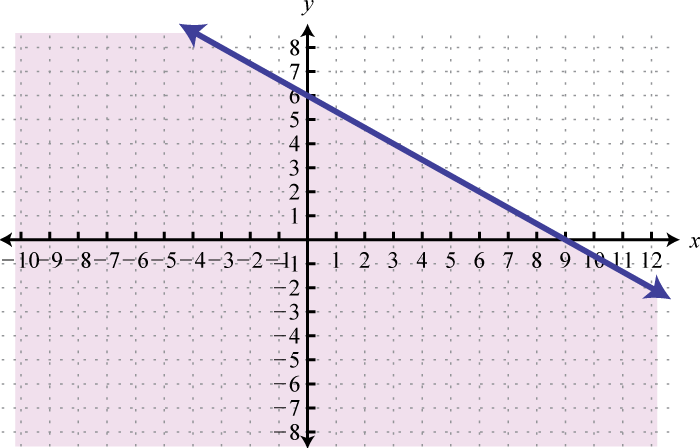
Малюнок\(\PageIndex{23}\) 7.
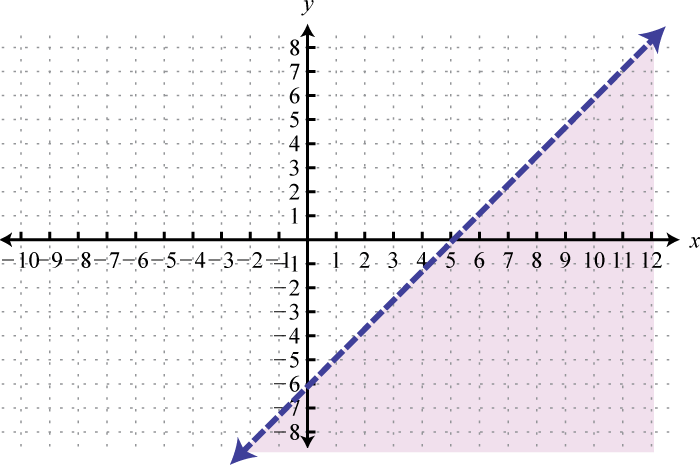
Малюнок\(\PageIndex{24}\) 9.
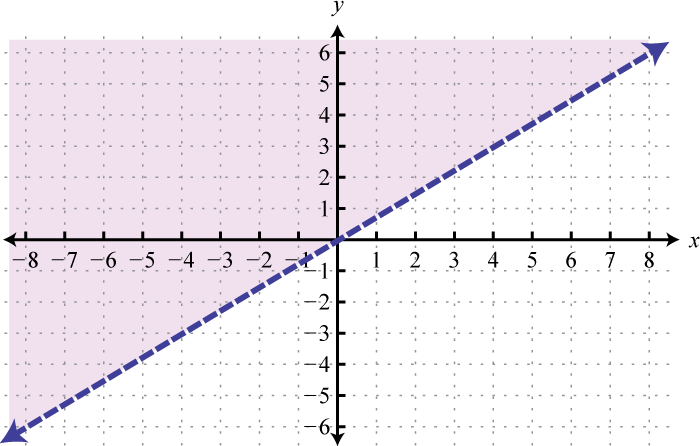
Малюнок\(\PageIndex{25}\) 11.
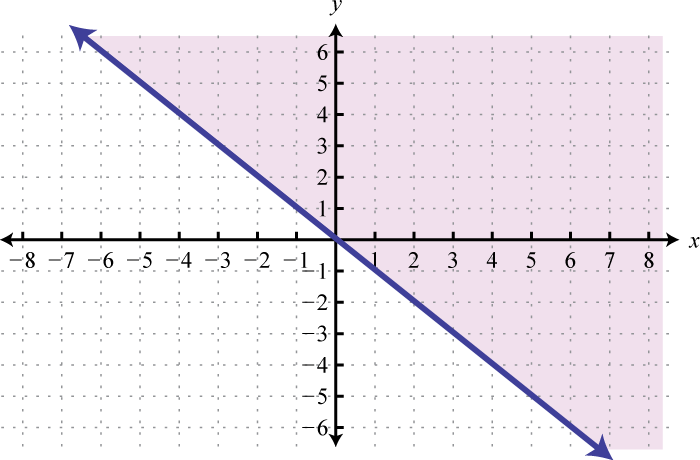
Малюнок\(\PageIndex{26}\) 13.
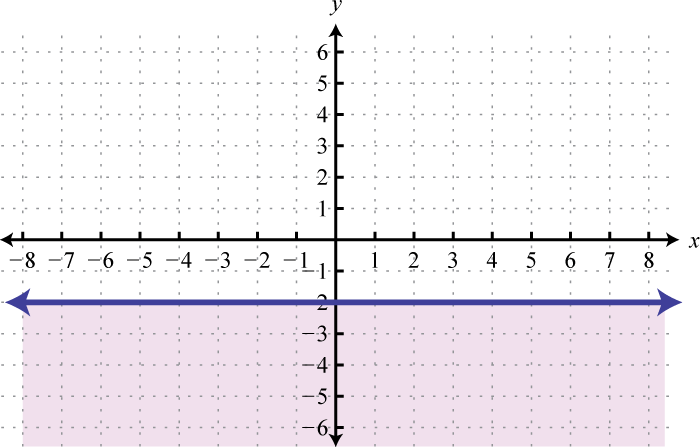
Малюнок\(\PageIndex{27}\) 15.
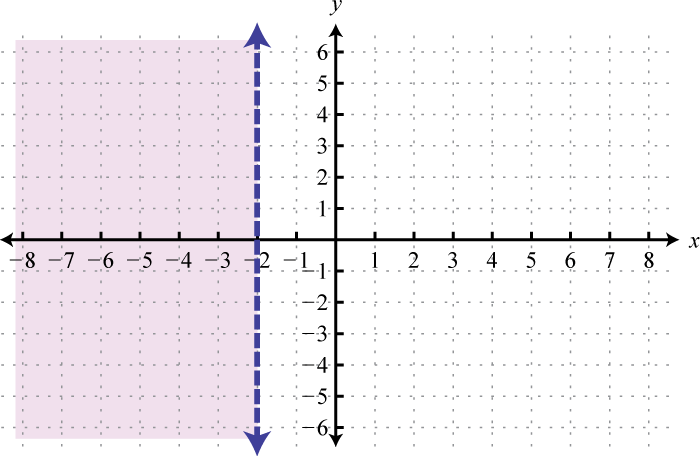
Малюнок\(\PageIndex{28}\) 17.
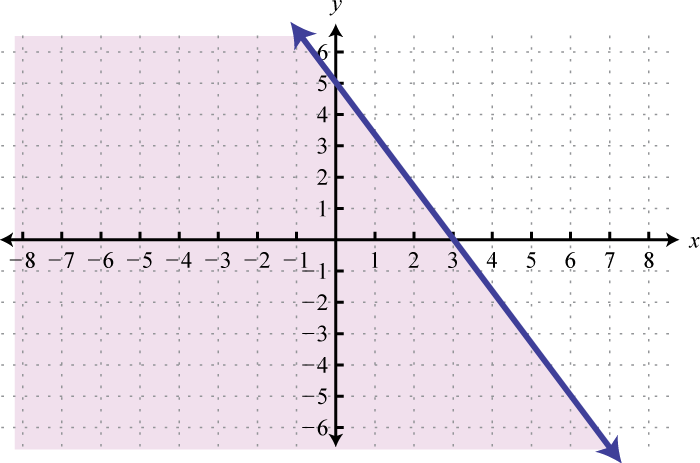
Малюнок\(\PageIndex{29}\) 19.
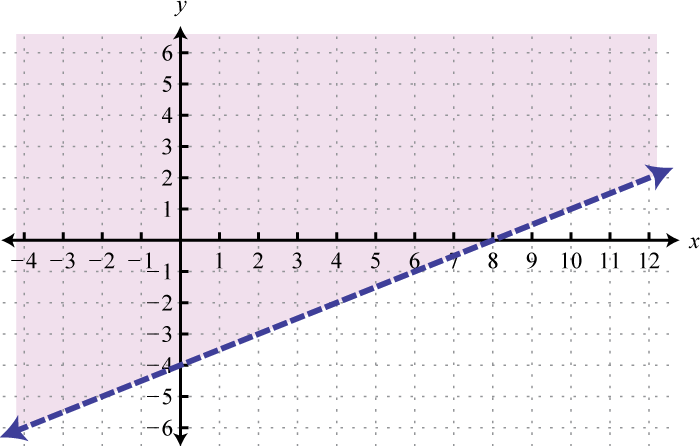
Малюнок\(\PageIndex{30}\) 21.
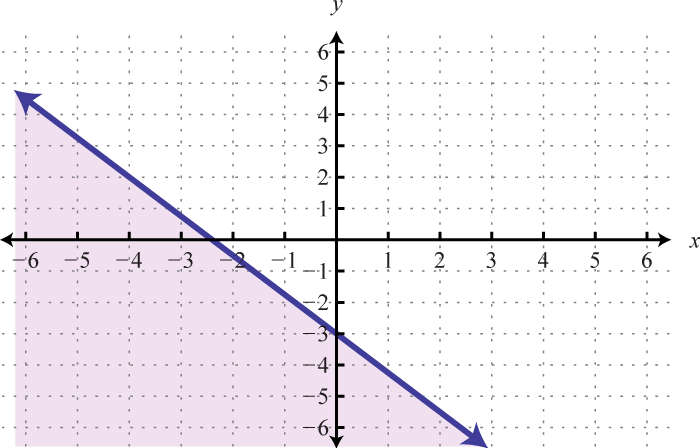
Малюнок\(\PageIndex{31}\) 23.
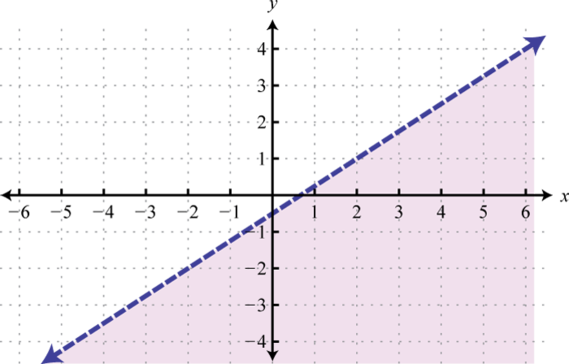
Малюнок\(\PageIndex{32}\) 25.
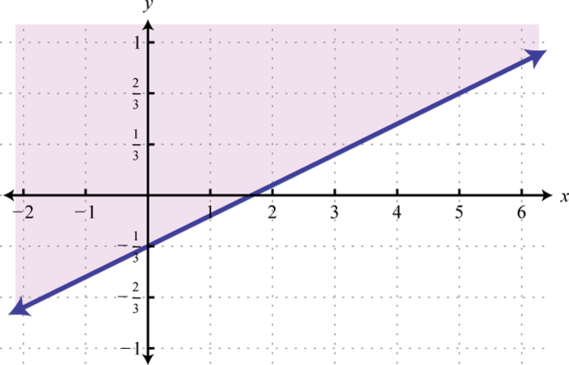
Малюнок\(\PageIndex{33}\) 27. \(y > 0\)
29. \(x < 0\)
31. \(y \geq k\)
Вправа\(\PageIndex{6}\)
Графік набору розв'язків.
- \(y ≤ x^{2} + 3\)
- \(y > x^{2} − 2\)
- \(y ≤ −x^{2}\)
- \(y ≥ −x^{2}\)
- \(y > (x + 1)^{2}\)
- \(y > (x − 2)^{2}\)
- \(y ≤ (x − 1)^{2} + 2\)
- \(y ≤ (x + 3)^{2} − 1\)
- \(y < −x^{2} + 1\)
- \(y > −(x − 2)^{2} + 1\)
- \(y ≥ |x| − 2\)
- \(y < |x| + 1\)
- \(y < |x − 3|\)
- \(y ≤ |x + 2|\)
- \(y > − |x + 1|\)
- \(y ≤ − |x − 2|\)
- \(y ≥ |x + 3| − 2\)
- \(y ≥ |x − 2| − 1\)
- \(y < − |x + 4| + 2\)
- \(y > − |x − 4| − 1\)
- \(y > x^{3} − 1\)
- \(y ≤ x^{3} + 2\)
- \(y ≤ \sqrt{x}\)
- \(y > \sqrt{x}− 1\)
- Прямокутна ручка повинна бути побудована з більшою\(200\) кількістю ніг огорожі. Запишіть лінійну нерівність через довжину\(l\) і ширину\(w\). Намалюйте графік всіх можливих варіантів вирішення цієї задачі.
- Компанія продає один продукт для,\($8\) а інший для\($12\). Скільки кожного товару потрібно продати, щоб доходи були не менше\($2,400\)? Дозвольте\(x\) представляти кількість продуктів, що продаються в\($8\) і нехай\(y\) представляють кількість продуктів, що продаються на\($12\). Напишіть лінійну нерівність через\(x\)\(y\) і намалюйте графік всіх можливих розв'язків.
- Відповідь
-
1.

Малюнок\(\PageIndex{34}\) 3.
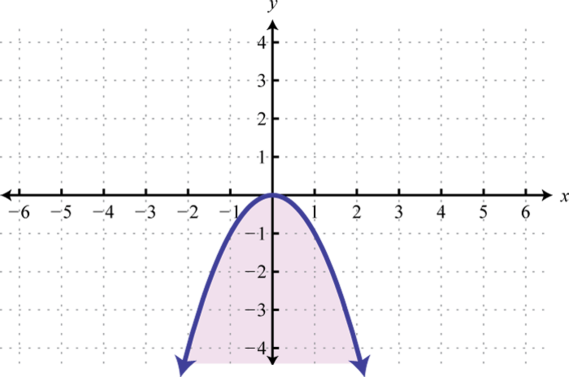
Малюнок\(\PageIndex{35}\) 5.
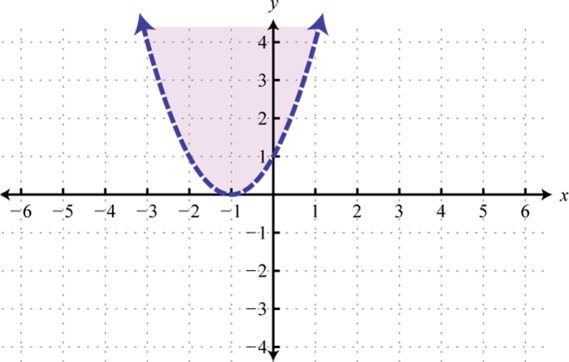
Малюнок\(\PageIndex{36}\) 7.
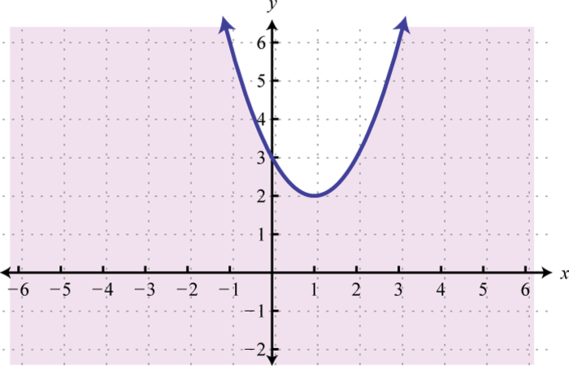
Малюнок\(\PageIndex{37}\) 9.
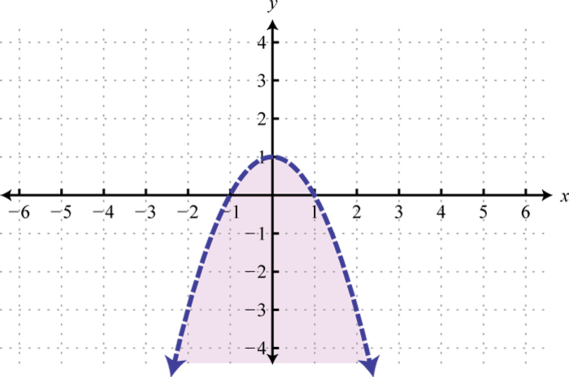
Малюнок\(\PageIndex{38}\) 11.
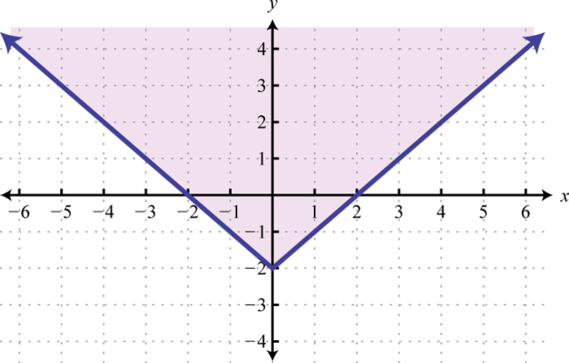
Малюнок\(\PageIndex{39}\) 13.
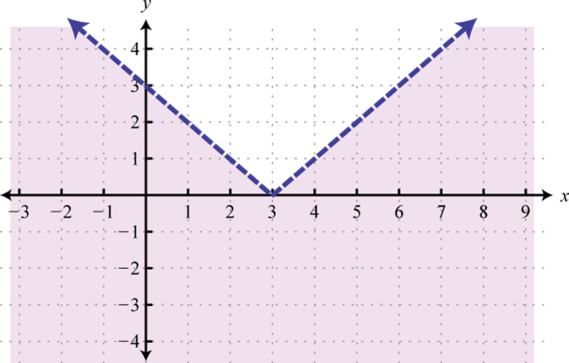
Малюнок\(\PageIndex{40}\) 15.
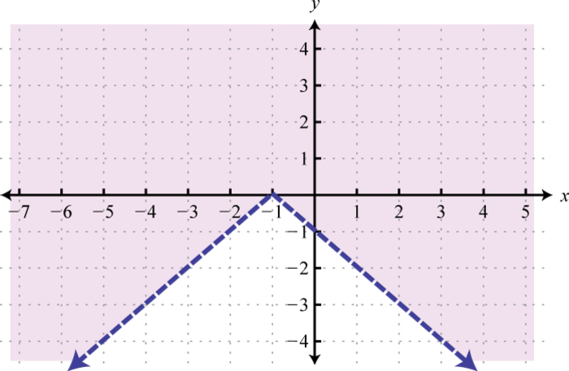
Малюнок\(\PageIndex{41}\) 17.
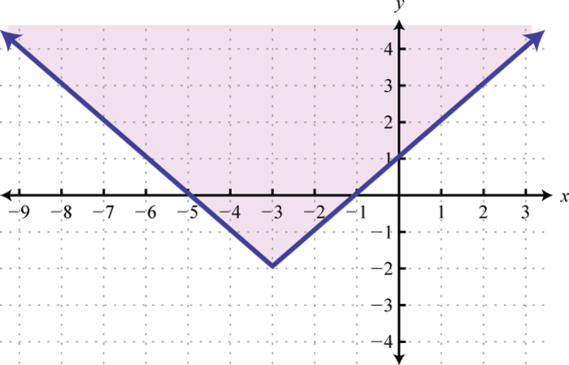
Малюнок\(\PageIndex{42}\) 19.
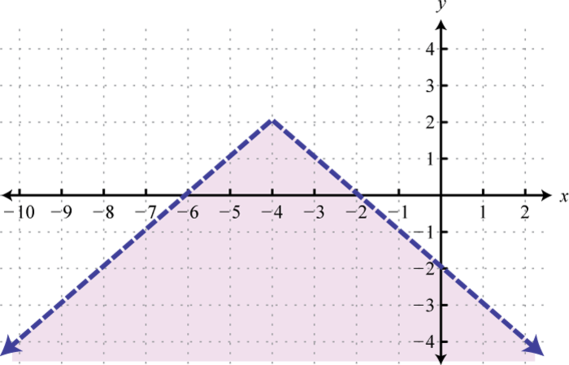
Малюнок\(\PageIndex{43}\) 21.
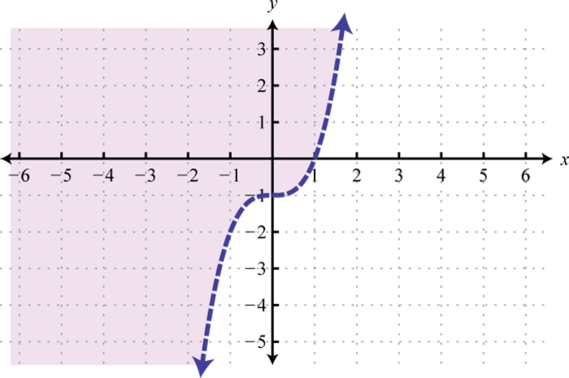
Малюнок\(\PageIndex{44}\) 23.
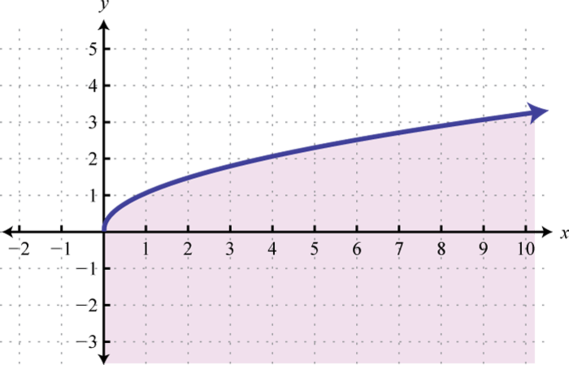
Малюнок\(\PageIndex{45}\) 25. \(l + w \leq 100\);
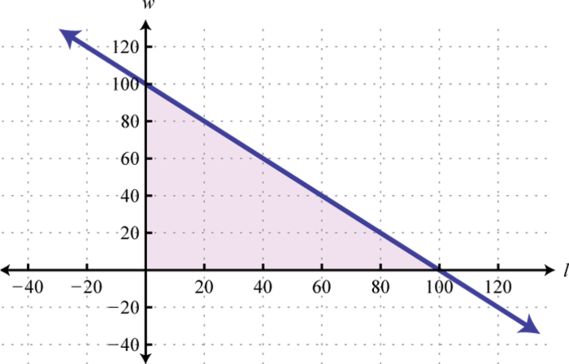
Малюнок\(\PageIndex{46}\)
