10.5: Графік квадратичних рівнянь

Цілі навчання

До кінця цього розділу ви зможете:

• Розпізнати графік квадратного рівняння у двох змінних
• Знайти вісь симетрії та вершину параболи
• Знайдіть перехоплення параболи
• Графік квадратичних рівнянь у двох змінних
• Вирішуйте максимальне та мінімальне застосування

Будьте готові

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

1. Графік рівняння$y=3x−5$ шляхом побудови точок.
   Якщо ви пропустили цю проблему, перегляньте [посилання].
2. Оцініть,$2x^2+4x−1$ коли$x=−3$
   Якщо ви пропустили цю проблему, перегляньте [посилання].
3. Оцініть,$−\frac{b}{2a}$ коли$a=13$ і b =$\frac{5}{6}$
   Якщо ви пропустили цю проблему, перегляньте [посилання].

Розпізнати графік квадратного рівняння у двох змінних

Ми склали графічні рівняння форми$Ax+By=C$. Ми назвали рівняння подібними до лінійних рівнянь, оскільки їх графіки є прямими лініями.

Тепер ми будемо графувати рівняння виду$y=ax^2+bx+c$. Ми називаємо це рівняння квадратним рівнянням у двох змінних.

Означення: КВАДРАТНЕ РІВНЯННЯ У ДВОХ ЗМІННИХ

Квадратне рівняння в двох змінних, де a, b і c є дійсними числами і$a\neq 0$, є рівнянням виду

$$y=ax^2+bx+c \nonumber$$

Так само, як ми почали графікувати лінійні рівняння шляхом побудови точок, ми зробимо те ж саме для квадратних рівнянь.

Давайте спочатку розглянемо графіку квадратного рівняння$y=x^2$. Ми виберемо цілочисельні значення x між −2 і 2 і знайдемо їх значення y. Див. Таблицю.

$y=x^2$
х	у
0	0
1	1
$−1$	1
2	4
$−2$	4

Зверніть увагу, коли ми дозволяємо$x=1$ і$x=−1$, ми отримали те ж значення для y.

$$\begin{array} {ll} {y=x^2} &{y=x^2} \\ {y=1^2} &{y=(−1)^2} \\ {y=1} &{y=1} \\ \nonumber \end{array}$$

Те ж саме сталося, коли ми пустили$x=2$ і$x=−2$.

Тепер ми будемо будувати точки, щоб показати графік$y=x^2$. Див. Малюнок.

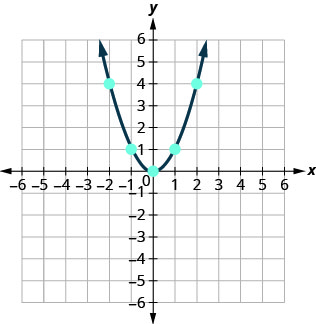
Графік не є лінією. Ця фігура називається параболою. Кожне квадратне рівняння має графік, який виглядає так.

У прикладі ви будете практикувати графіку параболи, намалювавши кілька пунктів.

Приклад$\PageIndex{1}$

$y=x^2-1$

Відповідь

Ми будемо графувати рівняння шляхом побудови точок.

Виберіть цілі числа для x, підставляйте їх у рівняння та вирішіть для y.
Запишіть значення впорядкованих пар на графіку.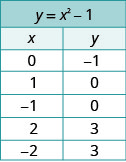
Намалюйте точки, а потім з'єднайте їх плавною кривою. Результатом буде графік рівняння.$y=x^2−1$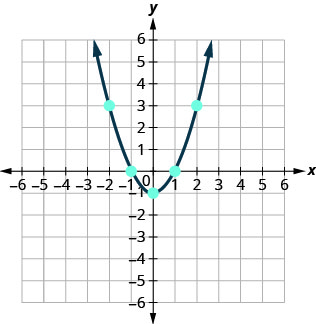

Приклад$\PageIndex{2}$

Графік$y=−x^2$.

Відповідь

Приклад$\PageIndex{3}$

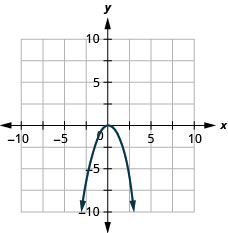
Графік$y=x^2+1$.

Відповідь

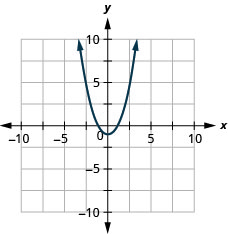
Як роблять рівняння$y=x^2$ і$y=x^2−1$ differ? What is the difference between their graphs? How are their graphs the same?

Всі параболи форми$y=ax^2+bx+c$ відкриваються вгору або вниз. Див. Малюнок.

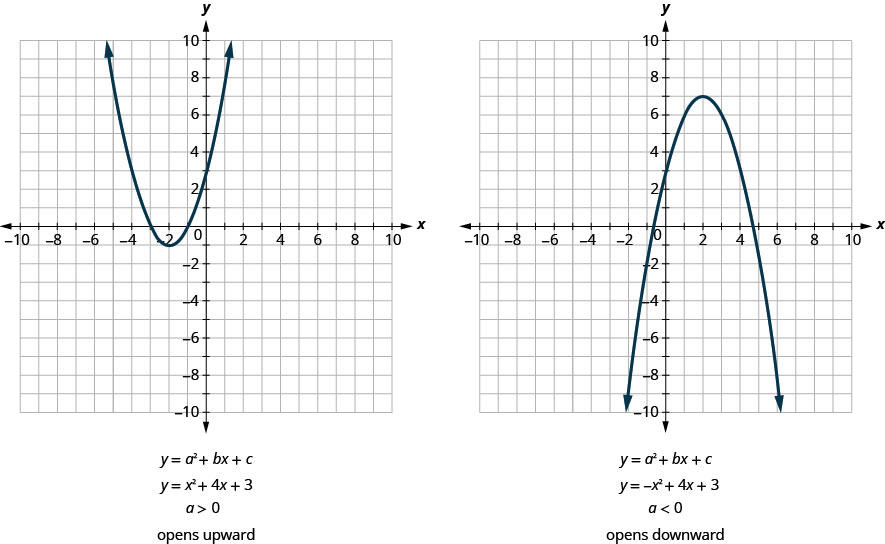
Зверніть увагу, що єдиною відмінністю в двох рівняннях є негативний знак перед рівнянням другого графіка на малюнку.$x^2$ Коли$x^2$ термін позитивний, парабола відкривається вгору, а коли$x^2$ термін негативний, парабола відкривається вниз.

Визначення: ОРІЄНТАЦІЯ ПАРАБОЛИ

Для квадратного рівняння$y=ax^2+bx+c$, якщо:

Приклад$\PageIndex{4}$

Визначте, відкривається кожна парабола вгору або вниз:

1. $y=−3x^2+2x−4$
2. $y=6x^2+7x−9$

Відповідь

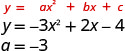
		Так як «а» негативний, то парабола відкриється вниз.
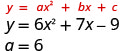
		Так як «а» позитивне, парабола відкриється вгору.

Приклад$\PageIndex{5}$

Визначте, відкривається кожна парабола вгору або вниз:

1. $y=2x^2+5x−2$
2. $y=−3x^2−4x+7$

Відповідь

1. вгору
2. вниз

Приклад$\PageIndex{6}$

Визначте, відкривається кожна парабола вгору або вниз:

1. $y=−2x^2−2x−3$
2. $y=5x^2−2x−1$

Відповідь

1. вниз
2. вгору

Знайти вісь симетрії та вершину параболи

Подивіться ще раз на Малюнок. Ви бачите, що ми могли б скласти кожну параболу навпіл і що одна сторона буде лежати поверх іншої? «Лінія згину» - це лінія симетрії. Ми називаємо її віссю симетрії параболи.

Ми знову показуємо ті ж два графіки з віссю симетрії червоним кольором. Див. Малюнок.

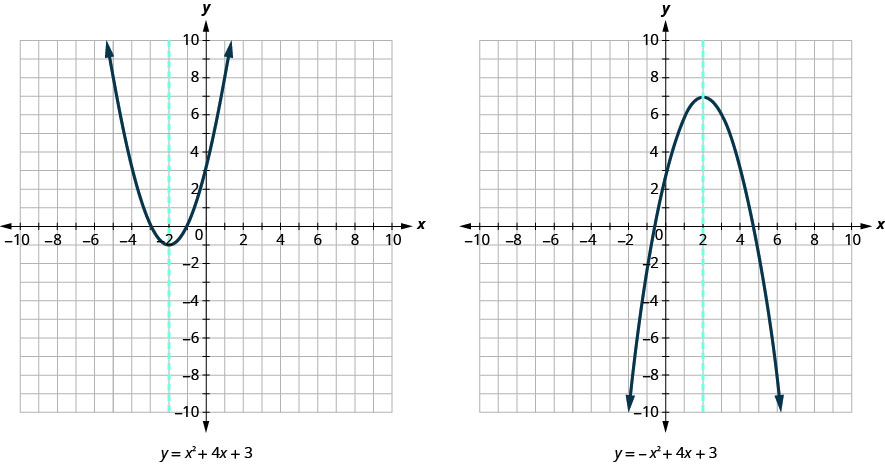
Рівняння осі симетрії можна вивести за допомогою квадратичної формули. Опустимо тут деривацію і приступимо безпосередньо до використання результату. Рівняння осі симетрії графа$y=ax^2+bx+c$ дорівнює x=$−\frac{b}{2a}$.

Отже, щоб знайти рівняння симетрії кожної з парабол, які ми намалювали вище, підставимо в формулу x=$−\frac{b}{2a}$.

Малюнок. Це рівняння пунктирних червоних ліній?

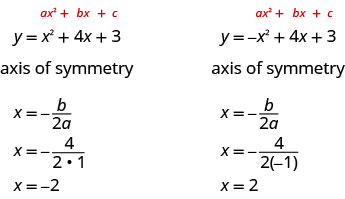
Точка на параболі, яка знаходиться на осі симетрії, є найнижчою або найвищою точкою на параболі, в залежності від того, відкривається парабола вгору або вниз. Ця точка називається вершиною параболи.

Ми можемо легко знайти координати вершини, тому що ми знаємо, що вона знаходиться на осі симетрії. Це означає, що його x -координата є$−\frac{b}{2a}$. Щоб знайти y -координату вершини, підставимо значення координати x в квадратне рівняння.

Означення: ВІСЬ СИМЕТРІЇ ТА ВЕРШИНА ПАРАБОЛИ

Для параболи з рівнянням$y=ax^2+bx+c$:

• Віссю симетрії параболи є лінією x=$−\frac{b}{2a}$.
• Вершина знаходиться на осі симетрії, тому її x -координата дорівнює$−\frac{b}{2a}$.

Щоб знайти y -координату вершини, підставляємо x=$−\frac{b}{2a}$ в квадратне рівняння.

Приклад$\PageIndex{7}$

Для параболи$y=3x^2−6x+2$ знаходимо:

1. вісь симетрії і
2. вершина.

Відповідь

1.
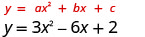
Вісь симетрії - лінія x=$−\frac{b}{2a}$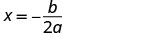
Підставляємо значення a, b в рівняння.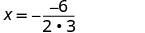
Спростити		х=1
		Віссю симетрії є лінія x=1
2.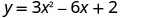
Вершина знаходиться на лінії симетрії, тому її x -координата буде x=1
Заставте x = 1 у рівняння і вирішіть для y.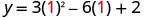
Спростити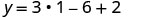
Це y -координата.		y=−1 Вершина є (1, −1).

Приклад$\PageIndex{8}$

Для параболи$y=2x^2−8x+1$ знаходимо:

1. вісь симетрії і
2. вершина.

Відповідь

1. х=2
2. (2, −7)

Приклад$\PageIndex{9}$

Для параболи$y=2x^2−4x−3$ знаходимо:

1. вісь симетрії і
2. вершина.

Відповідь

1. х=1
2. (1, −5)

Знайдіть перехоплення параболи

Коли ми графували лінійні рівняння, ми часто використовували x - і y -перехоплення, щоб допомогти нам графікувати лінії. Знаходження координат перехоплювачів допоможе нам також графувати параболи.

Пам'ятайте, при y -перехопленні значення x дорівнює нулю. Отже, щоб знайти y -перехоплення, підставляємо x=0 в рівняння.

Давайте знайдемо y -перехоплення двох парабол, показаних на малюнку нижче.

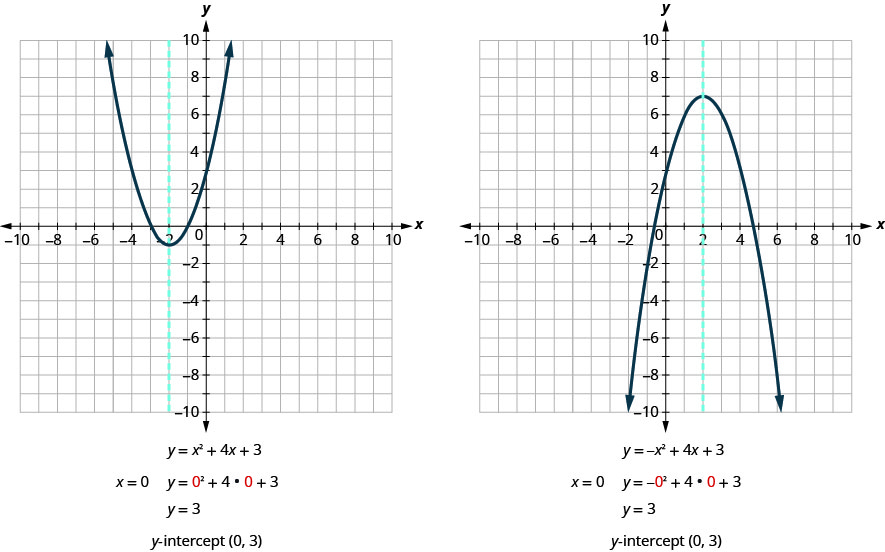
При перехопленні x значення y дорівнює нулю. Щоб знайти x -перехоплення, підставляємо$y=0$ в рівняння. Іншими словами, нам потрібно буде вирішити рівняння$0=ax^2+bx+c$ для x.

$$\begin{array} {ll} {y=ax^2+bx+c} \\ {0=ax^2+bx+c} \\ \nonumber \end{array}$$

Але рішення квадратних рівнянь, як це саме те, що ми зробили раніше в цьому розділі.

Тепер ми можемо знайти x -перехоплення двох парабол, показаних на малюнку.

Спочатку знайдемо x -перехоплення параболи з рівнянням$y=x^2+4x+3$.

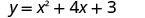Нехай y=0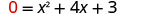
Фактор.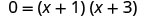
Використовуйте властивість нульового продукту.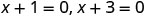
Вирішити.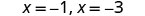
		Перехоплення x є (−1,0) та (−3,0).

Тепер ми знайдемо x -перехоплення параболи з рівнянням$y=−x^2+4x+3$.

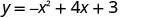Нехай y=0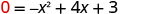
Ця квадратика не фактор, тому ми використовуємо квадратичну формулу.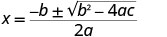
a=−1, b=4, c = 3.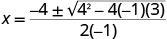
Спростити.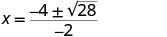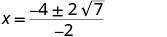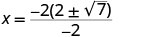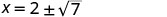
		X перехоплює є$(2+\sqrt{7},0)$ і$(2−\sqrt{7},0)$

Ми будемо використовувати десяткові наближення x-перехоплень, щоб ми могли знайти ці точки на графіку.

$$\begin{array} {l} {(2+\sqrt{7},0) \approx (4.6,0)} & {(2−\sqrt{7},0) \approx (-0.6,0)}\\ \nonumber \end{array}$$

Чи узгоджуються ці результати з нашими графіками? Див. Малюнок.

Визначення: ЗНАЙТИ ПЕРЕХОПЛЕННЯ ПАРАБОЛИ

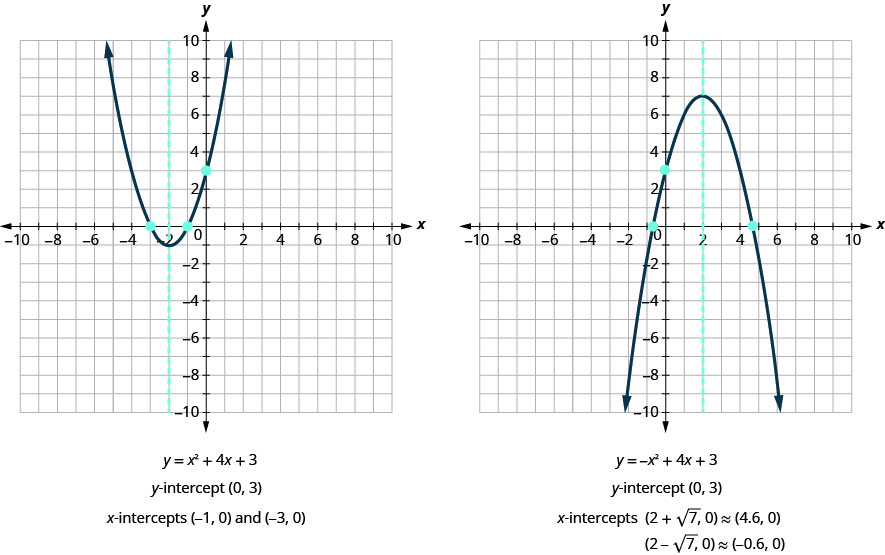
Щоб знайти перехоплення параболи з рівнянням$y=ax^2+bx+c$:

$$\begin{array}{ll} {\textbf{y-intercept}}& {\textbf{x-intercept}}\\ {\text{Let} x=0 \text{and solve the y}}& {\text{Let} y=0 \text{and solve the x}}\\ \nonumber \end{array}$$

Приклад$\PageIndex{10}$

Знайдіть перехоплення параболи$y=x^2−2x−8$.

Відповідь

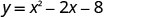
Щоб знайти y -перехоплення, нехай x = 0 і вирішити для y.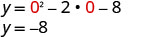
		Коли x=0, то y=−8. Перехоплення y - це точка (0, −8).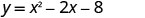
Щоб знайти x -перехоплення, нехай y=0 і вирішити для x.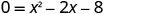
Вирішити шляхом факторингу.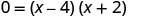

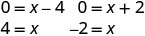
Коли y=0, то x=4 або x=−2. X-перехоплення — це точки (4,0) та (−2,0).

Приклад$\PageIndex{11}$

Знайдіть перехоплення параболи$y=x^2+2x−8$.

Відповідь

y: (0, −8); x: (−4,0), (2,0)

Приклад$\PageIndex{12}$

Знайдіть перехоплення параболи$y=x^2−4x−12$.

Відповідь

y: (0, −12); x: (6,0), (−2,0)

У цьому розділі ми розв'язували квадратні рівняння виду$ax^2+bx+c=0$. Ми розв'язали для xx і результати були розв'язками рівняння.

Зараз ми розглядаємо квадратичні рівняння в двох змінних форми$y=ax^2+bx+c$. Графіки цих рівнянь є параболами. X -перехоплення парабол відбуваються там, де y = 0.

Наприклад:

$$\begin{array}{cc} {\textbf{Quadratic equation}}&{\textbf{Quadratic equation in two variable}}\\ {}&{y=x^2−2x−15}\\ {x^2−2x−15}&{\text{Let} y=0, 0=x^2−2x−15}\\ {(x−5)(x+3)=0}&{0=(x−5)(x+3)}\\ {x−5=0, x+3=0}&{x−5=0, x+3=0}\\ {x=5, x=−3}&{x=5, x=−3}\\ {}&{(5,0) \text{and} (−3,0)}\\ {}&{\text{x-intercepts}}\\ \end{array}$$

Розв'язками квадратного рівняння є значення x -перехоплень.

Раніше ми бачили, що квадратні рівняння мають 2, 1 або 0 розв'язків. На графіках нижче наведені приклади парабол для цих трьох випадків. Оскільки розв'язки рівнянь дають x -перехоплення графів, то кількість х -перехоплень збігається з кількістю розв'язків.

Раніше ми використовували дискримінант для визначення кількості розв'язків квадратного рівняння виду$ax^2+bx+c=0$. Тепер ми можемо використовувати дискримінант, щоб сказати нам, скільки х -перехоплень є на графіку.

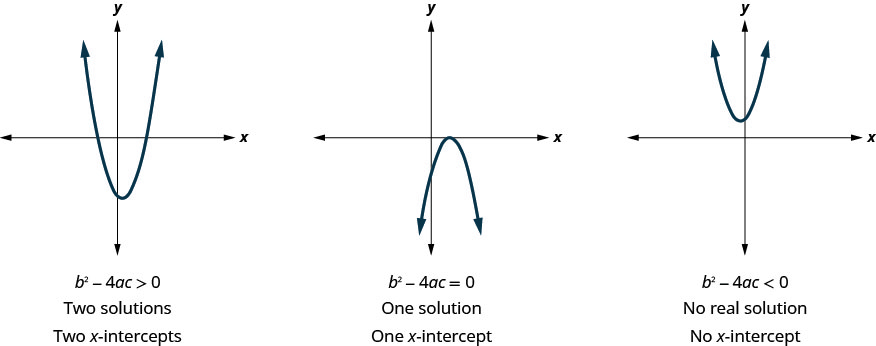
Перш ніж почати розв'язувати квадратне рівняння, щоб знайти значення x -перехоплень, ви можете оцінити дискримінант, щоб ви знали, скільки рішень слід очікувати.

Приклад$\PageIndex{13}$

Знайдіть перехоплення параболи$y=5x^2+x+4$.

Відповідь

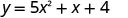
Щоб знайти y -перехоплення, нехай x = 0 і вирішити для y.	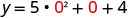	Коли x=0, то y=4. Y -перехоплення - це точка (0,4).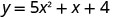
Щоб знайти x -перехоплення, нехай y=0 і вирішити для x.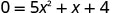
Знайти значення дискримінанту для прогнозування кількості розв'язків і так х -перехоплень.		b^2−4ac 1^2−4⋅5⋅4 1−80 −79
Оскільки значення дискримінанту від'ємне, реального рішення рівняння не існує.		Немає х -перехоплень.

Приклад$\PageIndex{14}$

Знайдіть перехоплення параболи$y=3x^2+4x+4$.

Відповідь

y: (0,4); х: немає

Приклад$\PageIndex{15}$

Знайдіть перехоплення параболи$y=x^2−4x−5$.

Відповідь

y: (0, −5); x: (5,0) (−1,0)

Приклад$\PageIndex{16}$

Знайдіть перехоплення параболи$y=4x^2−12x+9$.

Відповідь

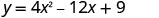
Щоб знайти y -перехоплення, нехай x = 0 і вирішити для y.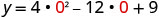
		Коли x=0, то y=9. Y -перехоплення - це точка (0,9).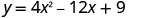
Щоб знайти x -перехоплення, нехай y=0 і вирішити для x.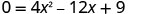
Знайти значення дискримінанту для прогнозування кількості розв'язків і так х -перехоплень.		b^2−4ac 12^2−4⋅4⋅9 144−144 0
		Оскільки значення дискримінанту дорівнює 0, реального розв'язку рівняння немає. Так що є один х -перехоплення.
Розв'яжіть рівняння шляхом факторингу ідеального квадратного триноміала.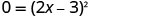
Використовуйте властивість нульового продукту.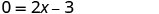
Вирішити для х.
		Коли y=0, то$\frac{3}{2}$ = x.
		X -перехоплення - це точка$(\frac{3}{2},0)$.

Приклад$\PageIndex{17}$

Знайдіть перехоплення параболи$y=−x^2−12x−36.$.

Відповідь

y: (0, −36); x: (−6,0)

Приклад$\PageIndex{18}$

Знайдіть перехоплення параболи$y=9x^2+12x+4$.

Відповідь

у: (0,4); х:$(−\frac{2}{3},0)$

Граф квадратних рівнянь у двох змінних

Тепер у нас є всі частини, які нам потрібні для того, щоб графікувати квадратне рівняння у двох змінних. Нам просто потрібно зібрати їх разом. У наступному прикладі ми побачимо, як це зробити.

Як графувати квадратне рівняння у двох змінних

Приклад$\PageIndex{19}$

Графік$y=x2−6x+8$.

Відповідь

Приклад$\PageIndex{20}$

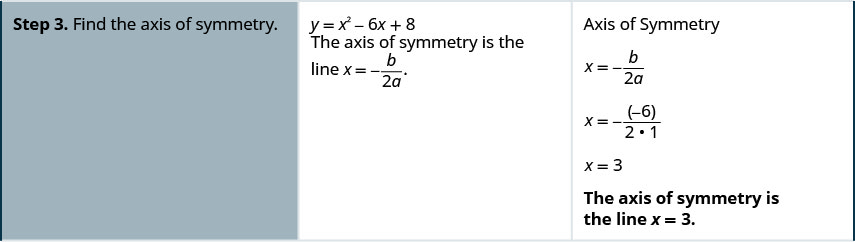
Графік параболи$y=x^2+2x−8$.

Відповідь

y: (0, −8); x: (2,0), (−4,0);
вісь: x = −1; вершина: (−1, −9);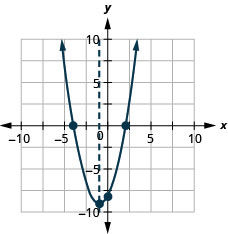

Приклад$\PageIndex{21}$

Графік параболи$y=x^2−8x+12$.

Відповідь

y: (0,12); x: (2,0), (6,0);
вісь: x = 4; вершина :( 4, −4);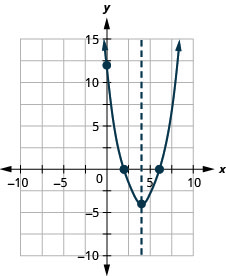

Означення: ГРАФ A КВАДРАТНЕ РІВНЯННЯ У ДВОХ ЗМІННИХ.

1. Запишіть квадратне рівняння з yy на одній стороні.
2. Визначте, чи відкривається парабола вгору або вниз.
3. Знайдіть вісь симетрії.
4. Знайдіть вершину.
5. Знайдіть y -перехоплення. Знайти точку, симетричну y -перехоплення поперек осі симетрії.
6. Знайдіть x -перехоплення.
7. Графік параболи.

Ми змогли знайти x -перехоплення в останньому прикладі шляхом факторингу. Ми також знаходимо x -перехоплення в наступному прикладі шляхом факторингу.

Приклад$\PageIndex{22}$

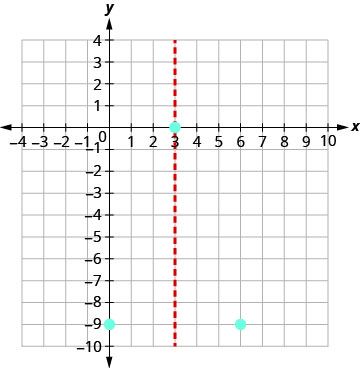
Графік$y=−x^2+6x−9$.

Відповідь

Рівняння y має з одного боку.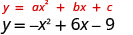
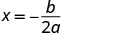
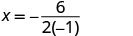
Оскільки a дорівнює −1, парабола відкривається вниз. Щоб знайти вісь симетрії, знайдіть$x=−\frac{b}{2a}$.		Вісь симетрії дорівнює x=3. Вершина знаходиться на рядку x=3.
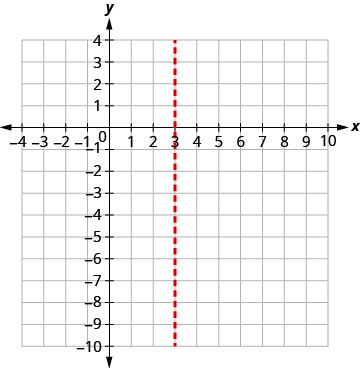
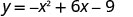
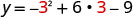
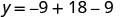
Знайти y, коли x=3.		Вершина дорівнює (3,0).
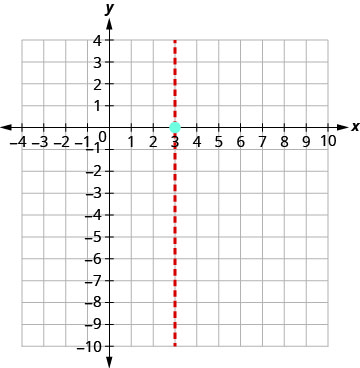
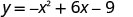
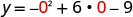
Перехоплення y відбувається, коли x = 0. Заміна x=0. Спростити. Точка (0, −9) — це три одиниці ліворуч від лінії симетрії. Точка три одиниці праворуч від лінії симетрії дорівнює (6, −9). Точка симетрична до y- перехоплення є (6, −9)		(0, −9).
X -перехоплення відбувається, коли y=0.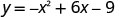
Заміна y=0.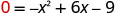
Фактор GCF.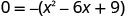
Фактор триноміалу.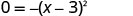
Вирішити для х.
З'єднайте точки, щоб графувати параболу.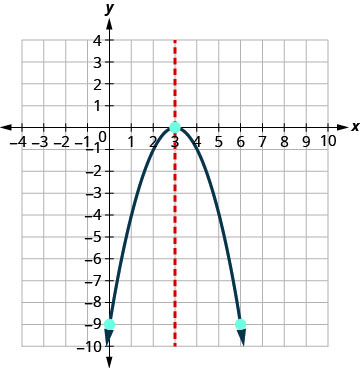

Приклад$\PageIndex{23}$

Графік параболи$y=−3x^2+12x−12$.

Відповідь

y: (0, −12); x: (2,0);
вісь: x = 2; вершина :( 2,0);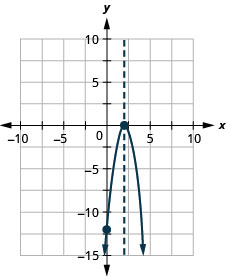

Приклад$\PageIndex{24}$

Графік параболи$y=25x^2+10x+1$.

Відповідь

y: (0,1); x: (−15,0);
вісь: x = −15; вершина :( −15,0);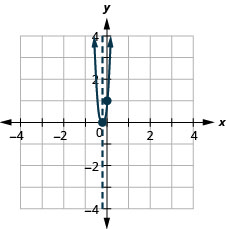

Для графа$y=−x^2+6x−9$ the vertex and the х -перехоплення були ті ж точки. Пам'ятайте, як дискримінант визначає кількість розв'язків квадратного рівняння? Дискримінант рівняння$0=−x^2+6x−9$ is 0, so there is only one solution. That means there is only one х -перехоплює, і це вершина параболи.

Скільки х -перехоплень ви очікуєте побачити на графіку$y=x^2+4x+5$?

Приклад$\PageIndex{25}$

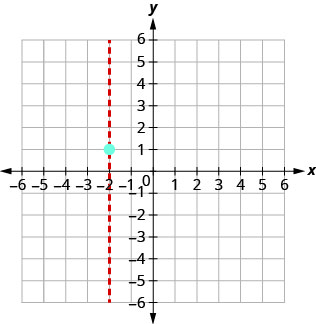
Графік$y=x^2+4x+5$.

Відповідь

Рівняння має y з одного боку.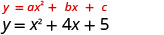
Оскільки a дорівнює 1, парабола відкривається вгору.
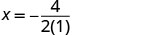
$x=−\frac{b}{2a}$.		x=−2.
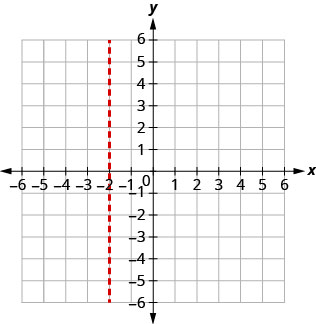
Вершина знаходиться на рядку x=−2.
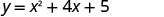
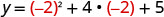
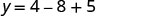
Знайти y, коли x=−2.		(−2,1).
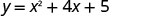
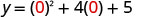
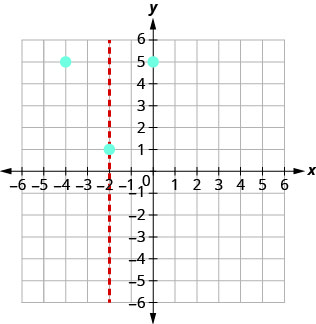
Перехоплення y відбувається, коли x = 0. Заміна x=0. Спростити. Точка (0,5) - дві одиниці праворуч від лінії симетрії. Точка на дві одиниці ліворуч від лінії симетрії дорівнює (−4,5).		(0,5). (−4,5)
X - перехоплення відбувається при y=0.
Заміна y=0. Перевірте дискримінант.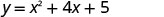
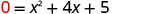
		$b^2−4ac$ $42−4⋅15$ $16−20$ $−4$
Оскільки значення дискримінанту негативне, рішення немає і тому немає х- перехоплення. З'єднайте точки, щоб графувати параболу. Можливо, ви захочете вибрати ще дві точки для більшої точності.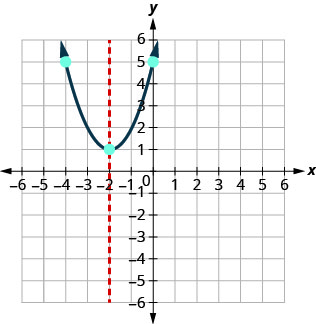

Приклад$\PageIndex{26}$

Графік параболи$y=2x^2−6x+5$.

Відповідь

y: (0,5); x: немає;
вісь:$x=\frac{3}{2}$; вершина:$(\frac{3}{2},\frac{1}{2})$;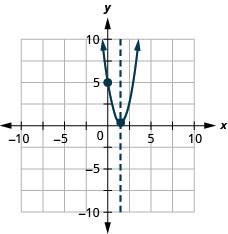

Приклад$\PageIndex{27}$

Графік параболи$y=−2x^2−1$.

Відповідь

y: (0, −1); x:none;
вісь: x = 0; вершина :( 0, −1);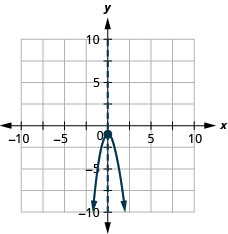

Знайти y -перехоплення шляхом підстановки x = 0 у рівняння легко, чи не так? Але нам потрібно було використовувати квадратичну формулу, щоб знайти x -перехоплення в прикладі. Ми знову будемо використовувати квадратичну формулу в наступному прикладі.

Приклад$\PageIndex{28}$

Графік$y=2x^2−4x−3$.

Відповідь

Рівняння y має одну сторону. Оскільки a дорівнює 2, парабола відкривається вгору.
Щоб знайти вісь симетрії, знайдіть$x=−\frac{b}{2a}$		Вершина дорівнює x=1
Вершина на рядку x=1.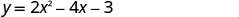
Знайти y, коли x=1	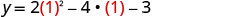	(1, −5)
Перехоплення y відбувається, коли x = 0.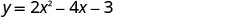
Замінник x=0.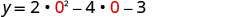
Спростити.		Перехоплення y - це (0, −3)
Точка (0, −3) - одна одиниця ліворуч від лінії симетрії. Точка на одну одиницю праворуч від лінії симетрії дорівнює (2, −3)		Точка симетрична до y- перехоплення дорівнює (2, −3).
X -перехоплення відбувається, коли y = 0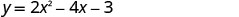
Замінник y=0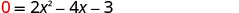
Використовуйте квадратичну формулу.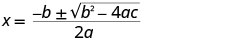
Підставляємо в значення a, b, c.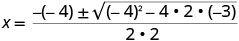
Спростити.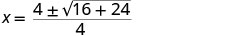
Спростити всередині радикалу.
Спростити радикал.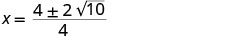
Фактор GCF.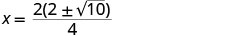
Видаліть загальні фактори.
Запишіть як два рівняння.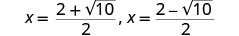
Орієнтовні значення.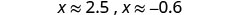
		Наближені значення x- перехоплень є (2,5,0) і (−0,6,0).
Графік параболи за допомогою знайдених точок.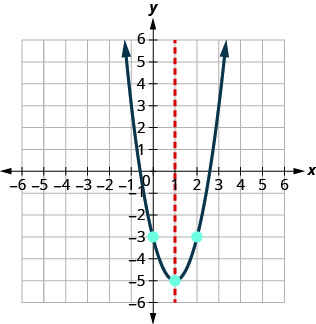

Приклад$\PageIndex{29}$

Графік параболи$y=5x^2+10x+3$.

Відповідь

y: (0,3); x: (−1,6,0), (−0,4,0);
вісь: x = −1; вершина :( −1, −2);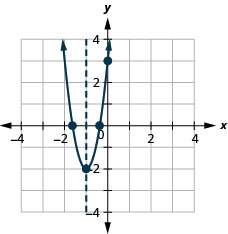

Приклад$\PageIndex{30}$

Графік параболи$y=−3x^2−6x+5$.

Відповідь

y: (0,5); x: (0,6,0), (−2,6,0);
вісь: x = −1; вершина :( −1,8);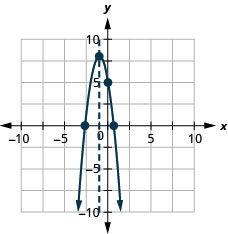

Вирішуйте максимальне та мінімальне застосування

Знання того, що вершина параболи є найнижчою або найвищою точкою параболи, дає нам простий спосіб визначити мінімальне або максимальне значення квадратного рівняння. y -координата вершини є мінімальним y -значенням параболи, яка відкривається вгору. Це максимальне y -значення параболи, яка відкривається вниз. Див. Малюнок.

Означення: МІНІМАЛЬНІ АБО МАКСИМАЛЬНІ ЗНАЧЕННЯ КВАДРАТНОГО РІВНЯННЯ

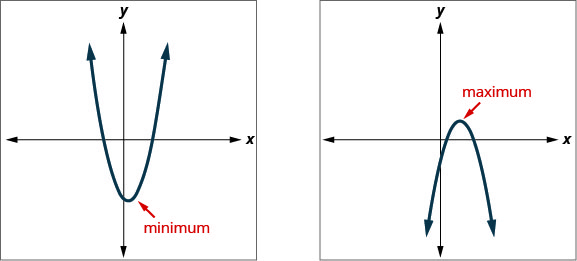
y -координата вершини графа квадратного рівняння є

• мінімальне значення квадратного рівняння, якщо парабола відкривається вгору.
• максимальне значення квадратного рівняння, якщо парабола відкривається вниз.

Приклад$\PageIndex{31}$

Знайти мінімальне значення квадратного рівняння$y=x^2+2x−8$.

Відповідь

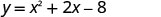
Оскільки a позитивний, парабола відкривається вгору.
Квадратне рівняння має мінімум.
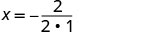
Знайдіть вісь симетрії.		x=−1
Вершина знаходиться на рядку x=−1.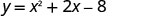
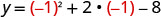
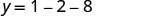
Знайти y, коли x=−1.		(−1, −9)
Оскільки парабола має мінімум, то y- координата вершини є мінімальним y- значенням квадратного рівняння.
Мінімальне значення квадратики дорівнює −9, і воно виникає, коли x=−1.
Покажіть графік, щоб перевірити результат.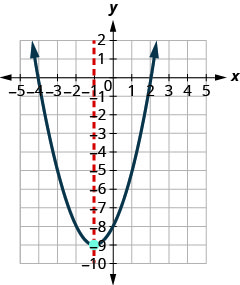

Приклад$\PageIndex{32}$

Знайти максимальне або мінімальне значення квадратного рівняння$y=x^2−8x+12$.

Відповідь

Мінімальне значення дорівнює −4, коли x=4.

Приклад$\PageIndex{33}$

Знайти максимальне або мінімальне значення квадратного рівняння$y=−4x^2+16x−11$.

Відповідь

Максимальне значення дорівнює 5, коли x=2.

Ми використали формулу

$$\begin{array} {l} {h=−16t^2+v_{0}t+h_{0}}\\ \nonumber \end{array}$$

обчислити висоту в футах, h, об'єкта, знятого вгору в повітря з початковою швидкістю$v_{0}$, після t секунд.

Ця формула являє собою квадратне рівняння в змінній tt, тому її графік є параболою. Вирішуючи координати вершини, ми можемо знайти, скільки часу знадобиться об'єкту, щоб досягти максимальної висоти. Потім ми можемо обчислити максимальну висоту.

Приклад$\PageIndex{34}$

Квадратне рівняння$h=−16t^2+v_{0}t+h_{0}$ моделює висоту волейбольного удару прямо вгору зі швидкістю 176 футів в секунду з висоти 4 футів.

1. Скільки секунд знадобиться волейболу, щоб досягти максимальної висоти?
2. Знайдіть максимальну висоту волейболу.

Відповідь

$h=−16t^2+176t+4$

Оскільки a негативний, парабола відкривається вниз.

Квадратне рівняння має максимум.

1.
$$\begin{array} {ll} {}&{t=−\frac{b}{2a}}\\ {\text{Find the axis of symmetry.}}& {t=−\frac{176}{2(−16)}}\\ {}&{t=5.5}\\ {}&{\text{The axis of symmetry is} t = 5.5}\\ {\text{The vertex is on the line} t=5.5}& {\text{The maximum occurs when} t =5.5 \text{seconds.}}\\ \nonumber \end{array}$$

2.

Знайти h, коли t=5.5.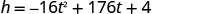
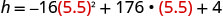
Скористайтеся калькулятором для спрощення.
		Вершина є (5.5,488)
Так як парабола має максимум, h- координата вершини є максимальним y -значенням квадратного рівняння.		Максимальне значення квадратики становить 488 футів, і це відбувається, коли t = 5,5 секунд.

Приклад$\PageIndex{35}$

Квадратне рівняння$h=−16t^2+128t+32$ використовується для знаходження висоти каменю, викинутого вгору з висоти 32 футів зі швидкістю 128 футів/сек. Скільки часу знадобиться, щоб камінь досяг своєї максимальної висоти? Яка максимальна висота? Круглі відповіді до найближчої десятої.

Відповідь

Щоб досягти максимальної висоти 288 футів, знадобиться 4 секунди.

Приклад$\PageIndex{36}$

Іграшкова ракета, знята вгору з землі зі швидкістю 208 футів/сек, має квадратне рівняння$h=−16t^2+208t$. Коли ракета досягне максимальної висоти? Якою буде максимальна висота? Круглі відповіді до найближчої десятої.

Відповідь

Щоб досягти максимальної висоти 676 футів, знадобиться 6,5 секунди.

Отримайте доступ до цих онлайн-ресурсів для отримання додаткових інструкцій та практики побудови графічних квадратних рівнянь:

• Графічні квадратичні функції
• Як ви графуєте квадратичну функцію?
• Графік квадратичних рівнянь

Ключові концепції

• Графік кожного квадратного рівняння є параболою.
• Орієнтація параболи Для квадратного рівняння$y=ax^2+bx+c$, якщо
  • a> 0, парабола відкривається вгору.
  • a<0, парабола відкривається вниз.
• Вісь симетрії та вершина параболи для параболи з рівнянням$y=ax^2+bx+c$:
  • Віссю симетрії параболи є лінія$x=−\frac{b}{2a}$.
  • Вершина знаходиться на осі симетрії, тому її x -координата дорівнює$−\frac{b}{2a}$.
  • Щоб знайти y -координату вершини, підставляємо$x=−\frac{b}{2a}$ в квадратне рівняння.
• Знайти Перехоплення Параболи Щоб знайти перехоплення параболи з рівнянням$y=ax^2+bx+c$:
  $$\begin{array} {ll} {\textbf{y-intercept}}&{\textbf{x-intercepts}}\\ {\text{Let} x=0 \text{and solve for y}}&{\text{Let} y=0 \text{and solve for x}}\\ \nonumber \end{array}$$
• Графік квадратного рівняння у двох змінних
  1. Запишіть квадратне рівняння з yy на одній стороні.
  2. Визначте, чи відкривається парабола вгору або вниз.
  3. Знайдіть вісь симетрії.
  4. Знайдіть вершину.
  5. Знайдіть y -перехоплення. Знайти точку, симетричну y -перехоплення поперек осі симетрії.
  6. Знайдіть x -перехоплення.
  7. Графік параболи.
• Мінімальні або максимальні значення квадратного рівняння
  • y - координата вершини графа квадратного рівняння є
  • мінімальне значення квадратного рівняння, якщо парабола відкривається вгору.
  • максимальне значення квадратного рівняння, якщо парабола відкривається вниз.

Глосарій

вісь симетрії

Віссю симетрії є вертикальна лінія, що проходить через середину параболи$y=ax^2+bx+c$.

парабола

Графік квадратного рівняння в двох змінних є параболою.

квадратне рівняння у двох змінних

Квадратне рівняння в двох змінних, де a, b і c є дійсними числами і$a \ge 0$ є рівнянням виду$y=ax^2+bx+c$.

вершина

Точка на параболі, яка знаходиться на осі симетрії, називається вершиною параболи; це найнижча або найвища точка на параболі, в залежності від того, відкривається парабола вгору або вниз.

x -перехоплення параболи

X -перехоплення - це точки на параболі, де$y=0$.

y -перехоплення параболи

Y -перехоплення - це точка на параболі, де$x=0$.