Глава 10 Огляд вправ
- Page ID
- 58749
Глава 10 Огляд вправ
10.1 Розв'язування квадратних рівнянь за допомогою властивості квадратного кореня
У наступних вправах вирішуйте, використовуючи властивість Square Root.
\(x^2=100\)
- Відповідь
-
\(x=\pm10\)
\(y^2=144\)
\(m^2−40=0\)
- Відповідь
-
\(m=\pm2\sqrt{10}\)
\(n^2−80=0\)
\(4a^2=100\)
- Відповідь
-
\(a=\pm5\)
\(2b^2=72\)
\(r^2+32=0\)
- Відповідь
-
немає рішення
\(t^2+18=0\)
\(\frac{4}{3}v^2+4=28\)
- Відповідь
-
\(v=\pm3\sqrt{2}\)
\(\frac{2}{3}w^2−20=30\)
\(5c^2+3=19\)
- Відповідь
-
\(c=\pm\frac{4\sqrt{5}}{5}\)
\(3d^2−6=43\)
У наступних вправах вирішуйте, використовуючи властивість Square Root.
\((p−5)^2+3=19\)
- Відповідь
-
p=1, 9
\((q+4)^2=9\)
\((u+1)^2=45\)
- Відповідь
-
\(u=−1\pm3\sqrt{5}\)
\((z−5)^2=50\)
\((x−\frac{1}{4})^2=\frac{3}{16}\)
- Відповідь
-
\(x=\frac{1}{4}\pm\frac{\sqrt{3}}{4}\)
\((y−\frac{2}{3})^2=\frac{2}{9}\)
\((m−7)^2+6=30\)
- Відповідь
-
\(m=7\pm2\sqrt{6}\)
\((n−4)^2−50=150\)
\((5c+3)^2=−20\)
- Відповідь
-
немає рішення
\((4c−1)^2=−18\)
\(m^2−6m+9=48\)
- Відповідь
-
\(m=3\pm4\sqrt{3}\)
\(n^2+10n+25=12\)
\(64a^2+48a+9=81\)
- Відповідь
-
a=−32, 34
\(4b^2−28b+49=25\)
10.2 Розв'язувати квадратні рівняння за допомогою завершення квадрата
У наступних вправах завершіть квадрат, щоб зробити ідеальний квадратний триноміал. Потім запишіть результат у вигляді біноміального квадрата.
\(x^2+22x\)
- Відповідь
-
\((x+11)^2\)
\(y^2+6y\)
\(m^2−8m\)
- Відповідь
-
\((m−4)^2\)
\(n^2−10n\)
\(a^2−3a\)
- Відповідь
-
\((a−\frac{3}{2})^2\)
\(b^2+13b\)
\(p^2+\frac{4}{5}p\)
- Відповідь
-
\((p+\frac{2}{5})^2\)
\(q^2−13q\)
У наступних вправах вирішуйте, виконавши квадрат.
\(c^2+20c=21\)
- Відповідь
-
с=1, −21
\(d^2+14d=−13\)
\(x^2−4x=32\)
- Відповідь
-
x=−4, 8
\(y^2−16y=36\)
\(r^2+6r=−100\)
- Відповідь
-
немає рішення
\(t^2−12t=−40\)
\(v^2−14v=−31\)
- Відповідь
-
\(v=7\pm3\sqrt{2}\)
\(w^2−20w=100\)
\(m^2+10m−4=−13\)
- Відповідь
-
\(m=−9,−1\)
\(n^2−6n+11=34\)
\(a^2=3a+8\)
- Відповідь
-
\(a=\frac{3}{2}\pm\frac{\sqrt{41}}{2}\)
\(b^2=11b−5\)
\((u+8)(u+4)=14\)
- Відповідь
-
\(u=−6\pm2\sqrt{2}\)
\((z−10)(z+2)=28\)
\(3p^2−18p+15=15\)
- Відповідь
-
p=0, 6
\(5q^2+70q+20=0\)
\(4y^2−6y=4\)
- Відповідь
-
\(y=−\frac{1}{2}, 2\)
\(2x^2+2x=4\)
\(3c^2+2c=9\)
- Відповідь
-
\(c=−\frac{1}{3}\pm\frac{2\sqrt{7}}{3}\)
\(4d^2−2d=8\)
10.3 Розв'язування квадратних рівнянь за квадратичною формулою
У наступних вправах вирішуйте за допомогою квадратичної формули.
\(4x^2−5x+1=0\)
- Відповідь
-
\(x=14, 1\)
\(7y^2+4y−3=0\)
\(r^2−r−42=0\)
- Відповідь
-
\(r=−6, 7\)
\(t^2+13t+22=0\)
\(4v^2+v−5=0\)
- Відповідь
-
\(v=−\frac{5}{4}, 1\)
\(2w^2+9w+2=0\)
\(3m^2+8m+2=0\)
- Відповідь
-
\(m=\frac{−4\pm\sqrt{10}}{3}\)
\(5n^2+2n−1=0\)
\(6a^2−5a+2=0\)
- Відповідь
-
немає реального рішення
\(4b^2−b+8=0\)
\(u(u−10)+3=0\)
- Відповідь
-
\(u=5\pm2\sqrt{2}\)
\(5z(z−2)=3\)
\(\frac{1}{8}p^2−\frac{1}{5}p=−\frac{1}{20}\)
- Відповідь
-
\(p=\frac{4\pm\sqrt{6}}{5}\)
\(\frac{2}{5}q^2+\frac{3}{10}q=\frac{1}{10}\)
\(4c^2+4c+1=0\)
- Відповідь
-
\(c=−\frac{1}{2}\)
\(9d^2−12d=−4\)
У наступних вправах визначте кількість розв'язків кожного квадратного рівняння.
- \(9x^2−6x+1=0\)
- \(3y^2−8y+1=0\)
- \(7m^2+12m+4=0\)
- \(5n^2−n+1=0\)
- Відповідь
-
- 1
- 2
- 2
- жоден
- \(5x^2−7x−8=0\)
- \(7x^2−10x+5=0\)
- \(25x^2−90x+81=0\)
- \(15x^2−8x+4=0\)
У наступних вправах визначте найбільш підходящий метод (Факторинг, Квадратний корінь або Квадратна формула), який слід використовувати для вирішення кожного квадратного рівняння.
- \(16r^2−8r+1=0\)
- \(5t^2−8t+3=9\)\(3(c+2)^2=15\)
- Відповідь
-
- фактор
- Квадратична формула
- квадратний корінь
- \(4d^2+10d−5=21\)
- \(25x^2−60x+36=0\)
- \(6(5v−7)^2=150\)
10.4 Розв'язуйте програми, змодельовані квадратними рівняннями
У наступних вправах вирішуйте за допомогою методів факторингу, принципу квадратного кореня або квадратної формули.
Знайдіть два послідовних непарних числа, твір яких дорівнює 323.
- Відповідь
-
Два послідовних непарних числа, добуток яких дорівнює 323, є 17 і 19, і −17 і −19.
Знайдіть два послідовних парних числа, твір яких дорівнює 624.
Трикутний банер має площу 351 квадратний сантиметр. Довжина підстави на два сантиметри довше, ніж в чотири рази більше висоти. Знайдіть висоту і довжину підстави.
- Відповідь
-
Висота банера - 13 см, а довжина бортика - 54 см.
Юлій побудував трикутну вітрину для своєї колекції монет. Висота вітрини на шість дюймів менше, ніж в два рази більше ширини підстави. Площа задньої частини корпусу становить 70 квадратних дюймів. Знайдіть висоту і ширину корпусу.
Плиткова мозаїка у формі прямокутного трикутника використовується як кут прямокутної доріжки. Гіпотенуза мозаїки становить 5 футів. Одна сторона мозаїки в два рази довше, ніж інша сторона. Які довжини сторін? Округлити до найближчої десятої.

- Відповідь
-
Довжини сторін мозаїки - 2,2 і 4,4 фута.
Прямокутний шматок фанери має діагональ, яка вимірює на два фути більше ширини. Довжина фанери в два рази більше ширини. Яка довжина діагоналі фанери? Округлити до найближчої десятої.
Парадна прогулянка від вулиці до будинку Пем займає площу 250 квадратних футів. Його довжина в два менше, ніж в чотири рази більше ширини. Знайдіть довжину і ширину тротуару. Округлити до найближчої десятої.
- Відповідь
-
Ширина передньої ходьби становить 8,1 фута, а її довжина - 30,8 футів.
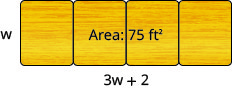
Для випускного вечора Софії кілька столів однакової ширини будуть розташовані впритул, щоб дати сервірувальний стіл загальною площею 75 квадратних футів. Загальна довжина столів буде в два більше, ніж в три рази більше ширини. Знайдіть довжину і ширину сервірувального столу, щоб Софія могла придбати скатертину правильного розміру. Круглий відповідь до найближчої десятої.
Куля кидається вертикально в повітря зі швидкістю 160 футів/сек. Використовуйте формулу,\(h=−16t^2+v_{0}t\) щоб визначити, коли м'яч буде знаходитися на відстані 384 футів від землі. Округлити до найближчої десятої.
- Відповідь
-
М'яч досягне 384 футів на шляху вгору за 4 секунди, а на шляху вниз за 6 секунд.
Куля вистрілюється прямо вгору з землі зі швидкістю 320 футів/сек. Використовуйте формулу,\(h=−16t^2+v_{0}t\) щоб визначити, коли куля досягне 800 футів. Округлити до найближчої десятої.
10.5 Графік квадратичних рівнянь у двох змінних
У наступних вправах граф за допомогою побудови точки.
Графік\(y=x^2−2\)
- Відповідь
-
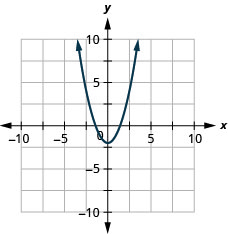
Графік\(y=−x^2+3\)
У наступних вправах визначте, чи відкриваються наступні параболи вгору або вниз.
\(y=−3x^2+3x−1\)
- Відповідь
-
вниз
\(y=5x^2+6x+3\)
\(y=x^2+8x−1\)
- Відповідь
-
вгору
А\(y=−4x^2−7x+1\)
У наступних вправах знайдіть
- осі симетрії і,
- вершина.
\(y=−x^2+6x+8\)
- Відповідь
-
- х=3
- (3,17)
\(y=2x^2−8x+1\)
У наступних вправах знайдіть x - і y -перехоплення.
\(y=x^2−4x+5\)
- Відповідь
-
y: (0,5); х: (5,0), (−1,0)
\(y=x^2−8x+15\)
\(y=x^2−4x+10\)
- Відповідь
-
y: (0,10); х: немає
\(y=−5x^2−30x−46\)
\(y=16x^2−8x+1\)
- Відповідь
-
у: (0,1); х: (14,0)
\(y=x^2+16x+64\)
У наступних вправах граф за допомогою перехоплень, вершини та осі симетрії.
\(y=x^2+8x+15\)
- Відповідь
-
y: (0,15); x: (−3,0), (−5,0);
вісь: x = −4; вершина :( −4, −1)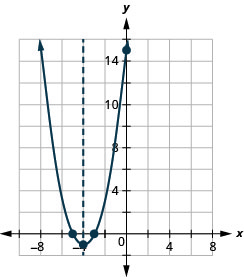
\(y=x^2−2x−3\)
\(y=−x^2+8x−16\)
- Відповідь
-
y: (0, −16); x: (4,0);
вісь: x = 4; вершина :( 4,0)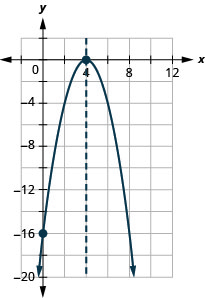
\(y=4x^2−4x+1\)
\(y=x^2+6x+13\)
- Відповідь
-
y: (0,13); x: немає;
вісь: x = −3; вершина :( −3,4)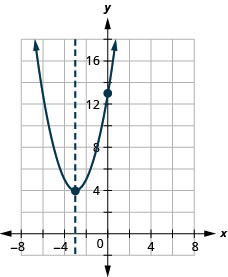
\(y=−2x^2−8x−12\)
\(y=−4x^2+16x−11\)
- Відповідь
-
y: (0, −11); x: (3.1,0), (0,9,0);
вісь: x = 2; вершина :( 2,5)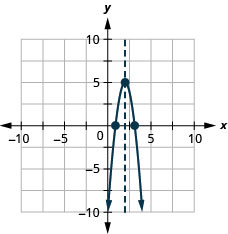
\(y=x^2+8x+10\)
У наступних вправах знайдіть мінімальне або максимальне значення.
\(y=7x^2+14x+6\)
- Відповідь
-
Мінімальним значенням є −1, коли\(x=−1\).
\(y=−3x^2+12x−10\)
У наступних вправах вирішуйте. Округлення відповідей до найближчої десятої.
М'яч кидається вгору від землі з початковою швидкістю 112 футів/сек. Використовуйте квадратне рівняння,\(h=−16t^2+112t\) щоб знайти, скільки часу потрібно м'ячу, щоб досягти максимальної висоти, а потім знайти максимальну висоту.
- Відповідь
-
За 3,5 секунди м'яч знаходиться на максимальній висоті 196 футів.
Дитячий садок огороджує прямокутну ділянку уздовж своєї будівлі, щоб діти могли грати на відкритому повітрі. Вони повинні максимізувати площу, використовуючи 180 футів огорожі з трьох сторін двору. Квадратне рівняння\(A=−2x^2+180x\) дає площу, A, двору для довжини, х, будівлі, яка буде межувати з двір. Знайдіть довжину будівлі, яка повинна межувати з двір, щоб максимально збільшити площу, а потім знайти максимальну площу.
Практика Тест
Використовуйте властивість квадратного кореня для вирішення квадратного рівняння:\(3(w+5)^2=27\).
- Відповідь
-
w=−2, −8
Використовуйте «Завершення квадрата» для вирішення квадратного рівняння:\(a^2−8a+7=23\)
Використовуйте квадратну формулу для вирішення квадратного рівняння:\(2m^2−5m+3=0\).
- Відповідь
-
м=1, 32
Розв'яжіть наступні квадратні рівняння. Використовуйте будь-який метод.
\(8v^2+3=35\)
\(3n^2+8n+3=0\)
- Відповідь
-
\(n=\frac{−4\pm\sqrt{7}}{3}\)
\(2b^2+6b−8=0\)
\(x(x+3)+12=0\)
- Відповідь
-
немає реального рішення
\(\frac{4}{3}y^2−4y+3=0\)
Використовуйте дискримінант для визначення кількості розв'язків кожного квадратного рівняння.
\(6p^2−13p+7=0\)
- Відповідь
-
2
\(3q^2−10q+12=0\)
Вирішіть за допомогою факторингу, властивості квадратного кореня або квадратної формули.
Знайдіть два послідовних парних числа, твір яких дорівнює 360.
- Відповідь
-
Два послідовних парних числа: −20 і −18 і 18 і 20.
Довжина діагоналі прямокутника на три більше ширини. Довжина прямокутника в три рази більше ширини. Знайдіть довжину діагоналі. (Округлення до найближчої десятої.)
Для кожної параболи знайдіть
- якими шляхами вона відкриває,
- вісь симетрії,
- вершина,
- x - і y -перехоплює, і
- максимальне або мінімальне значення.
\(y=3x^2+6x+8\)
- Відповідь
-
- вгору
- \(x=−1\)
- (−1,5)
- y: (0,8); х: немає; у: (0,8)
- мінімальне значення 5 при\(x=−1\).
\(y=x^2−4\)
\(y=x^2+10x+24\)
- Відповідь
-
- вгору
- \(x=−5\)
- (−5, −1)
- y: (0,24); x: (−6,0), (−4,0)
- мінімальне значення −5 при\(x=−1\)
\(y=−3x^2+12x−8\)
\(y=−x^2−8x+16\)
- Відповідь
-
- вниз
- \(x=−4\)
- (−4,32)
- у; (0,16); х: (−9,7,0), (1,7,0)
- максимальне значення 32 при\(x=−4\)
Графік наступних парабол, використовуючи перехоплення, вершину і вісь симетрії.
\(y=2x^2+6x+2\)
\(y=16x^2+24x+9\)
- Відповідь
-
y: (0,9); x: (−34,0)
вісь:\( x=−\frac{3}{4}\); вершина:\((−\frac{3}{4},0)\)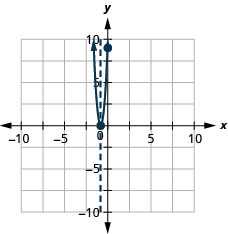
Вирішити.
Водний балон запускається вгору зі швидкістю 86 футів/сек. Використовуючи формулу h=−16t^2+86t, знайдіть, скільки часу знадобиться повітряній кулі, щоб досягти максимальної висоти, а потім знайдіть максимальну висоту. Округлити до найближчої десятої.