2.6: Нерівність

У главі 1 ми ввели натуральні числа$\mathbb{N}=\{1,2,3, \ldots\}$$\mathbb{W}=\{0,1,2,3, \ldots\}$, цілі числа та цілі числа$\mathbb{Z}=\{\ldots,-3,-2,-1,0,1,2,3, \ldots\}$. Пізніше в розділі ми ввели раціональні числа, числа виду$p/q$, де$p$ і$q$ є цілими числами. Ми зазначили, що як кінцеві, так і повторювані десяткові числа є раціональними числами. Кожне з цих чисел має унікальну позицію на числовому рядку (див. Рис.$\PageIndex{1}$).

Малюнок$\PageIndex{1}$: Розміщення чисел на числовому рядку.

Натуральні числа, цілі числа та цілі числа також є раціональними числами, оскільки кожне може бути виражено у вигляді$\frac{p}{q}$, де$p$ і$q$ є цілими числами. Наприклад,$0=\frac{0}{12}$,$4 = \frac{4}{1}$, і$-3=\frac{-12}{4}$. Дійсно, раціональні числа містять всі числа, які ми вивчали до цього моменту в курсі. Однак не всі числа є раціональними числами. Наприклад, розглянемо десяткове число$-3.10110111011110 \ldots$, яке ні закінчується, ні повторюється. Число$\sqrt{2}=1.414213562373095 \ldots$ також дорівнює десятковому числу, яке ніколи не закінчується і ніколи не повторюється. Аналогічне твердження можна зробити і щодо числа$\pi=3.141592653589793 \dots$ Кожне з цих ірраціональних (нераціональних) чисел також має унікальну позицію на числовому рядку (див. Рис.$\PageIndex{2}$).

Малюнок$\PageIndex{2}$: Розміщення чисел на числовому рядку.

Два інших ірраціональних числа, з якими ви можете зіткнутися в математичних дослідженнях, - це$e$ (константа Ейлера), яка приблизно дорівнює$e \approx 2.71828182845904 \ldots$, і$\phi$ (вимовляється «фі»), зване золотим перетином, яке дорівнює$\phi= \frac{1+\sqrt{5}}{2}$. Число$e$ виникає в додатках, що стосуються складних відсотків, ймовірності та інших областей математики. Число$\phi$ використовується на фінансових ринках, а також, можливо, співвідношення краси в мистецтві та архітектурі.

Реальні числа

Якщо об'єднати всі раціональні і ірраціональні числа в одну колекцію, то маємо набір чисел, який називається безліччю дійсних чисел. Безліч дійсних чисел позначається символом$\mathbb{R}$.

Кожна точка на числовому рядку пов'язана з унікальним дійсним числом. І навпаки, кожне дійсне число пов'язане з унікальною позицією на числовому рядку. Замість такої відповідності числовий рядок зазвичай називають реальною лінією.

Замовлення дійсних чисел

Дійсні числа впорядковуються на дійсному рядку таким чином, як ми впорядкували цілі числа на числовому рядку в Розділі 1 глави 1.

Замовлення на Real Line

Припустимо, що$a$ і$b$ є дійсними числами, розташованими на дійсній лінії, як показано нижче.

• Тому що$a$ брехня «зліва»$b$, ми говоримо, що$a$ це «менше, ніж»$b$, або в математичних символах,$a<b$. Символ нерівності$<$ читається «менше ніж».
• По черзі$b$ брехня «праворуч»$a$, тому ми також можемо сказати, що$b$ це «більше, ніж»$a$, або в математичних символах$b>a$. Символ нерівності$>$ читається «більше ніж».

Ось ще два символи нерівності, які ми будемо використовувати в цьому розділі.

Менше або дорівнює

Якщо ми хочемо сказати, що$a$ брехня «зліва»$b$, або розділяє ту ж позицію, що і$b$, то ми говоримо, що$a$ «менше або дорівнює»$b$ і пишемо$a ≤ b$. Символ нерівності$≤$ вимовляється «менше або дорівнює».

Більше або дорівнює

Якщо ми хочемо сказати, що$b$ брехня на «право»$a$, або розділяє ту ж позицію$a$, що і, то ми говоримо, що$b$ «більше або дорівнює»$a$ і пишемо$b≥ a$. Символ нерівності$≥$ вимовляється «більше або дорівнює».

Позначення Set-Builder

Математики використовують конструкцію, яка називається нотацією set-builder для опису множин або колекцій чисел. Загальна форма позначення set-builder виглядає наступним чином: $$\{x : \text { some statement about } x\} \nonumber$$ Наприклад, припустимо, що ми хочемо описати множину «всіх дійсних чисел, які менше»$2$. Ми могли б використовувати такі позначення: $$A=\{x : x<2\} \nonumber$$

Це читається вголос наступним чином: «$A$дорівнює набору всього$x$ такого,$x$ що менше»$2$. Деякі вважають за краще використовувати вертикальну смугу замість двокрапки. $$A=\{x \, | \, x<2\} \nonumber$$ У цьому тексті ми використовуємо двокрапку в позначеннях set-builder, але не соромтеся використовувати вертикальну смугу замість цього. Вони означають одне і те ж. Можна ще заперечити, що позначення трохи $$\{x : x<2\} \nonumber$$ розпливчасті. Одне заперечення може бути «Який тип цифр$x$ ви маєте на увазі? Ви хочете цілі числа, які менше двох або ви хочете дійсні числа, які менше двох?» Як бачите, це дійсне заперечення. Одним із способів вирішення цього заперечення є написання: $$A=\{x \in \mathbb{R} : x<2\} \quad \text { or } \quad A=\{x \in \mathbb{N} : x<2\} \nonumber$$ Перший$A$ читається «це набір усіх$x$,$R$ що менше двох», тоді як другий$A$ читається «- це набір усіх$x$$N$, що менше двох».

Set-будівельник Припущення

У цьому тексті, якщо немає конкретної посилання на набір бажаних чисел, ми будемо вважати,$\{x : x<2\}$ що позначення просять набір всіх дійсних чисел менше$2$.

На малюнку$\PageIndex {3}$ ми затінювали набір дійсних чисел$\{x : x<2\}$. Тому що

Малюнок$\PageIndex{3}$: Затінення чисел менше$2$.

«менше, ніж» - це те саме, що сказати «зліва», ми затінювали (червоним кольором) всі точки на реальній лінії, які лежать ліворуч від числа два. Зверніть увагу, що під номером два є «порожнє коло». Точка, що представляє число два, не затінена, тому що нас попросили лише затінювати числа, які строго менше двох.

Хоча затінення на малюнку$\PageIndex{3}$ цілком дійсне, значна частина інформації, наданої на малюнку,$\PageIndex{3}$ є непотрібною (і, можливо, відволікаючою). Нам потрібно лише позначити кінцеву точку та затінювати дійсні числа зліва від двох, як ми зробили при побудові малюнка$\PageIndex{4}$.

Малюнок$\PageIndex{4}$: Вам потрібно лише позначити кінцеву точку.

Для контрасту, припустимо замість цього, що нас попросять затінювати набір дійсних чисел$\{x : x\leq2\}$. Це означає, що ми повинні затінювати всі дійсні числа.

Малюнок$\PageIndex{5}$: Вам потрібно лише позначити кінцеву точку.

які є «менше або дорівнює$2$» або «ліворуч і включно»$2$. Отриманий набір розтушовують на рис$\PageIndex{5}$.

Зверніть увагу на різницю між цифрами$\PageIndex{4}$ і$\PageIndex{45}$. На малюнках$\PageIndex{4}$ ми затінюємо набір$\{x : x<2\}$,$2$ тому число залишається незаштрихованим (порожня точка). На$\PageIndex{5}$ малюнках ми затінюємо набір$\{x : x\leq2\}$,$2$ тому число затінено (заповнена крапка).

Приклад$\PageIndex{1}$

Заштрихуйте набір$\{x : x \geq-3\}$ на реальну лінію.

Рішення

Позначення$\{x : x \geq-3\}$ вимовляється «множина всіх дійсних чисел$x$ таких, що$x$ більше або дорівнює»$-3$. Таким чином, нам потрібно затінювати число$-3$ і всі дійсні числа праворуч від$-3$.

Вправа$\PageIndex{1}$

Тінь$\{x : x \leq 4\}$ на реальній лінії.

Відповідь

Приклад$\PageIndex{2}$

Використовуйте позначення set-builder, щоб описати набір дійсних чисел, які затінені на числовому рядку нижче.

Рішення

Число$-1$ не затінюється. Затінені лише$-1$ цифри зліва від. Це множина всіх дійсних чисел,$x$ таких,$x$ що «менше ніж»$-1$. Таким чином, ми опишемо цей набір наступними позначеннями set-builder: $$\{x : x<-1\} \nonumber$$

Вправа$\PageIndex{2}$

Використовуйте позначення set-builder для опису наступного набору дійсних чисел:

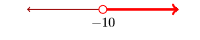
Відповідь

$\{x : x>-10\}$

Інтервальні позначення

У Прикладах$\PageIndex{1}$ і$\PageIndex{2}$ ми використовували позначення set-builder для опису множини дійсних чисел більше або рівних$-3$ і другий набір дійсних чисел менше$-1$. Існує ще одна математична символіка, звана інтервальними позначеннями, яка може бути використана для опису цих множин дійсних чисел. Розглянемо перший набір чисел з Приклад$\PageIndex{1}$,$\{x : x \geq-3\}$.

Помітаючи очі «зліва направо», ми використовуємо$[-3, \infty)$ для опису цей набір дійсних чисел. Деякі зауваження по порядку:

1. Кронштейн на лівому кінці означає, що$-3$ входить в комплект.
2. Коли ви рухаєтеся до правого кінця реального рядка, числа ростуть без обмежень. Отже,$\infty$ символ (позитивна нескінченність) використовується для позначення того, що ми включаємо всі дійсні числа праворуч від$-3$. Однак насправді$\infty$ це не число, тому ми використовуємо дужки, щоб вказати, що ми «не включаючи» цю вигадану точку.

Набір чисел з Прикладу$\PageIndex {1}$ є$\{x : x<-1\}$.

Помітаючи очі «зліва направо», цей набір дійсних чисел описується с$(-\infty,-1)$. Знову ж, коментарі по порядку:

1. Номер не$-1$ входить в цей набір. Щоб вказати, що він не включений, використовуємо дужку.
2. Коли ви рухаєтеся до лівого кінця реального рядка, числа зменшуються без обмежень. Отже,$-\infty$ символ (негативна нескінченність) використовується для позначення того, що ми включаємо всі дійсні числа зліва від$-1$. Знову ж таки,$-\infty$ це не фактичне число, тому ми використовуємо дужки, щоб вказати, що ми не включаємо цю «вигадану» точку.

Змітайте очі «зліва направо»

Якщо ви хочете застрахувати, що ви правильно використовуєте інтервальні позначення, розмістіть числа у вашому інтервальному позначенні в тому ж порядку, в якому вони зустрічаються, коли ви змітаєте очі «зліва направо» на реальному рядку.

Приємне резюме set-builder і інтервальне позначення представлено в таблиці$\PageIndex{1}$ в кінці розділу.

Еквівалентні нерівності

Як і рівняння, дві нерівності еквівалентні, якщо вони мають однакові набори розв'язків.

Додавання або віднімання однакової величини з обох сторін нерівності

$a$$b$Дозволяти і бути дійсними числами з $$a < b \nonumber$$
If$c$ є будь-яке дійсне число, то $$a + c<b+ c \nonumber$$ і $$a−c<b−c \nonumber$$ Тобто, додавання або віднімання однакової суми з обох сторін нерівності виробляє еквівалентну нерівність (не змінює рішення).

Приклад$\PageIndex{3}$

Вирішити для$x: \quad x-2 ≤ 7$. Намалюйте рішення на реальній лінії, а потім використовуйте set-builder та інтервальні позначення для опису вашого рішення.

Рішення

Щоб «скасувати» віднімання$2$, ми додаємо$2$ до обох сторін нерівності.

$$\begin{aligned} x-2 &\leq 7 & & \color {Red} \text { Original inequality. } \\ x-2+2 &\leq 7+2 & & \color {Red} \text { Add } 2 \text { to both sides. } \\ x &\leq 9 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber$$

Щоб затінювати дійсні числа менше або рівні$9$, ми затінюємо число$9$ і всі дійсні числа зліва від$9$.

Використовуючи нотації set-builder, рішення є$\{x : x \leq 9\}$. Використовуючи інтервальні позначення, рішення є$(-\infty, 9]$.

Вправа$\PageIndex{3}$

Використовуйте інтервальні позначення для опису рішення:$x−7 < −8$.

Відповідь

$(-\infty,-1)$

Якщо ми помножимо або ділимо обидві сторони нерівності на додатне число, ми маємо еквівалентну нерівність.

Множення або ділення на додатне число

$b$Дозволяти$a$ і бути дійсними числами с$a<b$. Якщо$c$ є дійсним додатним числом, то $$a c<b c \nonumber$$ і $$\dfrac{a}{c}<\dfrac{b}{c} \nonumber$$

Приклад$\PageIndex{4}$

Вирішіть для$x : \quad 3 x \leq-9$ Sketch рішення на реальній лінії, а потім використовуйте set-builder та інтервальні позначення для опису вашого рішення.

Рішення

Щоб «скасувати» множення на$3$, розділіть обидві сторони нерівності на$3$. Оскільки ми ділимо обидві сторони на додатне число, ми не змінюємо знак нерівності.

$$\begin{aligned} 3x & \leq -9 & & \color {Red} \text { Original inequality. } \\ \dfrac{3x}{3} & \leq \dfrac{-9}{3} & & \color {Red} \text { Divide both sides by } 3. \\ x & \leq -3 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber$$

Затіньте дійсні числа, менші або рівні$-3$.

Використовуючи нотації set-builder, рішення є$\{x : x \leq-3\}$. Використовуючи інтервальні позначення, рішення є$(-\infty,-3]$.

Вправа$\PageIndex{4}$

Використовуйте інтервальне позначення для опису рішення: $$2 x>-8 \nonumber$$

Відповідь

$(-4, \infty)$

Повернення знака нерівності

До цього моменту здається, що техніка розв'язання нерівностей в значній мірі ідентична техніці, яка використовується для вирішення рівнянь. Однак у цьому розділі ми зіткнемося з одним винятком.

Припустимо, ми починаємо з дійсної нерівності$-2 < 5$, потім множимо обидві сторони на$2$$3$, і$4$.

$$\begin{array}{rrrr}{-2<5} & {-2<5} & {-2<5} \\ {2(-2)<2(5)} & {3(-2)<3(5)} & {4(-2)<4(5)} \\ {-4<10} & {-6<15} & {-8<20}\end{array} \nonumber$$

Зверніть увагу, що в кожному випадку отримана нерівність залишається дійсною.

$\color{Red} \text {Caution! We’re about to make an error!}$

Почніть знову з$−2 < 5$, але на цей раз помножте обидві сторони на$−2$$−3$, і$−4$.

$$\begin{array}{rrrr}{-2<5} & {-2<5} & {-2<5} \\ {-2(-2)<-2(5)} & {\;-3(-2)<-3(5)} & {\;-4(-2)<-4(5)} \\ {4<-10} & {6<-15} & {8<-20}\end{array} \nonumber$$

У кожному з результуючих нерівностей символ нерівності вказує неправильний шлях!

Коли ви множите обидві сторони нерівності на негативне число, ви повинні змінити знак нерівності. Починаючи з$−2 < 5$, помножте обидві сторони на$−2$$−3$, і$−4$, але навпаки символ нерівності.

Деякі читачі можуть віддати перевагу більш формальній причині, чому ми змінюємо нерівність, коли ми множимо обидві сторони на негативне число. Припустимо, що$a<b$. Потім, віднімання$b$ з обох сторін дає результат$a−b<0$. Це означає, що$a−b$ є від'ємним числом. Тепер,$c$ якщо негативне число, то продукт$(a−b)c$ позитивний. Потім:

$$\begin{aligned}(a-b) c &>0 \\ a c-b c &>0 \\ a c-b c+b c &>0+b c \\ a c &>b c \end{aligned} \nonumber$$

Таким чином, якщо почати з$a<b$ і$c<0$, то$ac > bc$.

Множення або ділення на від'ємне число

$b$Дозволяти$a$ і бути дійсними числами с$a<b$. Якщо$c$ є дійсним від'ємним числом, то $$a c>b c \nonumber$$ і $$\dfrac{a}{c}>\dfrac{b}{c} \nonumber$$ Тобто при множенні або діленні обох сторін нерівності на від'ємне число необхідно повернути знак нерівності.

Приклад$\PageIndex{5}$

Вирішити для$x: \quad −2x<4$. Намалюйте рішення на реальній лінії, а потім використовуйте set-builder та інтервальні позначення для опису вашого рішення.

Рішення

Щоб «скасувати» множення на$−2$, розділіть обидві сторони на$−2$. Оскільки ми ділимо обидві сторони на негативне число, ми змінюємо знак нерівності.

$$\begin{aligned} -2 x&< 4 & & \color {Red} \text { Original inequality. } \\ \dfrac{-2x}{-2}&> \dfrac{4}{-2} & & \color {Red} \text { Divide both sides by }-2 \\ x&> -2 & & \color {Red} \text { Reverse the inequality sign. } \\ x&> -2 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber$$

Затіньте дійсні числа більше$−2$.

Використовуючи нотації set-builder, рішення є$\{x : x>-2\}$. Використовуючи інтервальні позначення, рішення є$(-2, \infty)$.

Вправа$\PageIndex{5}$

Використовуйте інтервальне позначення для опису рішення: $$−3x≥− 6 \nonumber$$

Відповідь

$(-\infty, 2]$

Кілька кроків

Іноді потрібно виконати послідовність кроків, щоб прийти до рішення.

Приклад$\PageIndex{6}$

Вирішити для$x: \quad 2 x +5> −7$. Намалюйте рішення на реальній лінії, а потім використовуйте set-builder та інтервальні позначення для опису вашого рішення.

Рішення

Щоб «скасувати» додавання$5$, відніміть$5$ з обох сторін нерівності.

$$\begin{aligned} 2x+5&> -7 & & \color {Red} \text { Original inequality. } \\ 2x+5-5&> -7-5 & & \color {Red} \text { Subtract } 5 \text { from both sides. } \\ 2x&> -12 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber$$

Щоб «скасувати» множення на$2$, розділіть обидві сторони на$2$. Оскільки ми ділимо обидві сторони на додатне число, ми не змінюємо знак нерівності.

$$\begin{aligned} \dfrac{2x}{2}& >\dfrac{-12}{2} & & \color {Red} \text { Divide both sides by } 2 \\ x&> -6 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber$$

Затіньте дійсні числа більше$−6$.

Використовуючи нотації set-builder, рішення є$\{x : x>-6\}$. Використовуючи інтервальні позначення, рішення є$(-6, \infty)$.

Вправа$\PageIndex{6}$

Використовуйте інтервальне позначення для опису рішення: $$3x-2 ≤4 \nonumber$$

Відповідь

$(-\infty, 2]$

Приклад$\PageIndex{7}$

Вирішити для$x: \quad 3 −5x ≤ 2x + 17$. Намалюйте рішення на реальній лінії, а потім використовуйте set-builder та інтервальні позначення для опису вашого рішення.

Рішення

Потрібно виділити терміни, що містять з одного$x$ боку нерівність. Почніть з віднімання$2x$ з обох сторін нерівності.

$$\begin{aligned} 3-5x &\leq 2x+17 & & \color {Red} \text { Original inequality. } \\ 3-5x-2x &\leq 2x+17-2x & & \color {Red} \text { Subtract } 2x \text { from both sides. } \\ 3-7x &\leq 17 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber$$

Продовжуємо виділяти терміни, що містять з одного$x$ боку нерівність. Відніміть$3$ з обох сторін.

$$\begin{aligned} 3-7x-3 &\leq 17-3 & & \color {Red} \text { Subtract } 3 \text { from both sides. } \\ -7x &\leq 14 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber$$

Щоб «скасувати» множення на$−7$, розділіть обидві сторони на$−7$. Оскільки ми ділимо обидві сторони на негативне число, ми змінюємо знак нерівності.

$$\begin{aligned} \dfrac{-7x}{-7} &\geq \dfrac{14}{-7} & & \color {Red} \text { Divide both sides by }-7 \\ x &\geq-2 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber$$

Використовуючи нотації set-builder, рішення є$\{x : x \geq-2\}$. Використовуючи інтервальні позначення, рішення є$[-2, \infty)$.

Вправа$\PageIndex{7}$

Використовуйте інтервальне позначення для опису рішення: $$4-x>2x +1 \nonumber$$

Відповідь

$(-\infty, 1)$

Очищаємо дроби від нерівності звичайним способом, множивши обидві сторони на найменш спільний знаменник.

Приклад$\PageIndex{8}$

Вирішити для$x : \quad \quad \dfrac{3}{4}-\dfrac{x}{12}>\dfrac{1}{3}$.

Рішення

Спочатку очистіть дроби від нерівності, помноживши обидві сторони на найменш спільний знаменник, який в даному випадку є$12$.

$$\begin{aligned} \dfrac{3}{4}-\dfrac{x}{12} &>\dfrac{1}{3} & & \color {Red} \text { Original inequality. } \\ 12\left[\dfrac{3}{4}-\dfrac{x}{12}\right] &>\left[\dfrac{1}{3}\right] 12 & & \color {Red} \text { Multiply both sides by } 12.\\ 12\left[\dfrac{3}{4}\right]-12\left[\dfrac{x}{12}\right] &>\left[\dfrac{1}{3}\right] 12 & &  \color {Red} \text { Distribute the } 12.\\ 9-x &>4 & &  \color {Red} \text { Cancel and Multiply. } \end{aligned} \nonumber$$

Щоб «скасувати» додавання$9$, відніміть$9$ з обох сторін.

$$\begin{aligned} 9-x-9 &> 4-9 & & \color {Red} \text { Subtract } 9 \text { from both sides. } \\ -x &> -5 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber$$

Ми могли б розділити обидві сторони на$−1$, але множення обох сторін на також$−1$ зробить роботу. Оскільки ми множимо обидві сторони на негативне число, ми змінюємо знак нерівності.

$$\begin{aligned} (-1)(-x) &< (-5)(-1) & & \color {Red} \text { Multiply both sides by }-1. \text { Reverse the inequality sign. } \\ x &< 5 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber$$

Затіньте дійсні числа менше, ніж$5$.

Використовуючи нотації set-builder, рішення є$\{x : x<5\}$. Використовуючи інтервальні позначення, рішення є$(-\infty, 5)$.

Вправа$\PageIndex{8}$

Використовуйте інтервальне позначення для опису рішення: $$\dfrac{2 x}{3}-\dfrac{3}{4} \geq-\dfrac{3}{2} \nonumber$$

Відповідь

$[-\frac{9}{8}, \infty)$

Очищаємо десяткові числа від нерівності звичайним способом, множивши обидві сторони на відповідну ступінь десять.

Приклад$\PageIndex{9}$

Вирішити для$x : \quad 3.25-1.2 x>4.6$.

Рішення

Спочатку очистіть десяткові числа від нерівності, множивши обидві сторони на$100$, що переміщує кожну десяткову крапку на два розряди вправо.

$$\begin{aligned} 3.25-1.2 x &>4.6 & & \color {Red} \text { Original inequality. }\\ 325-120 x &>460 & & \color {Red} \text { Multiply both sides by } 100.\\ 325-120 x-325 &>460-325 & & \color {Red} \text { Subtract } 325 \text { from both sides. }\\ -120 x &>135 & & \color {Red} \text { Simplify both sides. } \\ \dfrac{-120 x}{-120} &<\dfrac{135}{-120} & & \color {Red} \text { Divide both sides by } -120. \text { Reverse the inequality sign.}\\ x &<-\dfrac{27}{24} & & \color {Red} \text {Reduce to lowest terms.} \end{aligned} \nonumber$$

Затіньте дійсні числа менше, ніж$−27/24$.

Використовуючи нотації set-builder, рішення є$\{x : x<-27 / 24\}$. Використовуючи інтервальні позначення, рішення є$(-\infty,-27 / 24)$.

Вправа$\PageIndex{9}$

Використовуйте інтервальне позначення для опису рішення: $$2.3 x-5.62 \geq-1.4 \nonumber$$

Відповідь

$\big[\frac{211}{115}, \infty\big)$

Зведена таблиця Set-Builder та інтервальне позначення

Зведена таблиця множника і інтервальних позначень представлена в табл$\PageIndex{1}$.

Таблиця$\PageIndex{1}$: Приклади set-builder і інтервальних позначень.

Затінення на реальній лінії	Набір будівельник	Інтервал
	$\{x : x>-5\}$	$(-5, \infty)$
	$\{x : x \geq-5\}$	$[-5, \infty)$
	$\{x : x<-5\}$	$(-\infty,-5)$
	$\{x : x \leq-5\}$	$(-\infty,-5]$