1.22: Розв'язування квадратних рівнянь методом факторингу

Last updated
Save as PDF

Page ID: 58008

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Як вже говорилося раніше, рішення рівнянь залежить від типу рівняння під рукою. Ви можете переглянути рішення лінійних рівнянь у розділі 16. У цій главі піде мова про рішення квадратних рівнянь. Це рівняння, які містять другу ступінь змінної і нічого вище.

Приклад 20.1

Приклади квадратичних рівнянь:

а)$x^{2}-3 x-18=0$ - квадратне рівняння.

б)$x^{2}=81$ являє собою квадратне рівняння.

в)$4 x^{2}-36=0$ являє собою квадратне рівняння.

г) не$x^{3}-27=0$ є квадратним рівнянням, так як включає в себе змінну третього ступеня - розв'язування таких рівнянь в цьому класі ми не будемо обговорювати.

Розв'язування квадратних рівнянь

Розв'язування квадратних рівнянь передбачає три основних етапи. Ми розглянемо кожен з цих кроків, як ми приступимо до вирішення$x^{2}=100$.

Крок 1. Стандартна форма

Ми говоримо, що рівняння знаходиться в стандартній формі, якщо всі члени зібрані на одній стороні знака рівності, а на іншій стороні є тільки 0. Наприклад, рівняння a) і c) у попередньому прикладі є квадратними рівняннями в стандартній формі.

Якщо ми працюємо з рівнянням, яке не в стандартній формі, ми можемо легко отримати його до потрібної форми, додаючи або віднімаючи члени з обох сторін.

Наприклад,$x^{2}=100$ рівняння не в стандартній формі. Щоб отримати його до стандартного вигляду, віднімаємо 100 з обох сторін рівняння:

\[x^{2}=100\nonumber\]

\[-100 \quad-100\nonumber\]

\[\Longrightarrow x^{2}-100=0\nonumber\]

Примітка: Якщо рівняння під рукою вже в стандартному вигляді, то пропускаємо цей крок.

Крок 2. Фактор

Тепер, коли всі члени знаходяться на одній стороні рівняння, ми множимо квадратичний вираз під рукою. Непогано переглянути методи факторингу, введені в розділах 12, 13 і 14.

\ [\ begin {align*}
x^ {2} -100 &=0\
\\ Довгаста стрілка x^ {2} - (10) ^ {2} &= 0\\
\ Довгострілка (x+10) (x+10) &=0
\ end {align*}\ nonnumber\]

Крок 3. Використовувати властивість нульового продукту

Нерухомість продукту

Якщо$A \cdot B=0$ то$A=0$ або$B=0$.

Причина, чому ця властивість корисна при вирішенні квадратних рівнянь, полягає в тому, що після того, як ви поставили своє рівняння в стандартній формі та враховані, ви точно опинилися в ситуації, коли ви можете застосувати властивість нульового продукту.

\[(x-10)(x+10)=0\nonumber\]

перекладається на:

\[(x-10)=0 \text { or }(x+10)=0\nonumber\]

і тепер обидва рівняння під рукою лінійні, і їх вирішення - це питання виділення змінної за допомогою деяких алгебраїчних маніпуляцій. Зверніть увагу, що тепер у вас є два лінійних рівняння, кожне дасть своє рішення. Отже, ваше початкове квадратне рівняння матиме два рішення.

\[x − 10 = 0 \text{ gives }x = 10\nonumber\]

\[x + 10 = 0 \text{ gives }x = −10\nonumber\]

Отже, розв'язками рівняння$x^{2}=100$ є$x=10$ і$x=-10$.

Крок 4. Перевірка (необов'язково)

Це не є обов'язковим (якщо питання конкретно не просить його), але це хороша звичка перевіряти, чи правильні отримані рішення. Щоб перевірити, чи правильні наші рішення, нам потрібно підставити 10 і -10 у вихідне рівняння$x^{2}=100$.

Ми легко бачимо, що$(10)^{2}=100$ і$(-10)^{2}=100,$ тому обидва рішення працюють.

Приклад 20.2

Вирішити:

а)$5(x-2)(x+3)=0$

Зверніть увагу, що це рівняння вже в стандартній формі і враховано. Щоб застосувати властивість нульового продукту для

\[5(x-2)(x+3)=0\nonumber\]

Спочатку розділимо обидві сторони рівняння на 5 (або множимо на$\frac{1}{5}$):

\[\frac{5(x-2)(x+3)}{5}=\frac{0}{5}\nonumber\]

Це дає

\[(x-2)(x+3)=0\nonumber\]

Тепер застосовуємо властивість нульового продукту

\[(x-2)=0 \text { or }(x+3)=0\nonumber\]

\[x-2=0 \text{ gives } x=2\nonumber\]

\[x + 3 = 0 \text{ gives } x = −3\nonumber\]

Отже, розв'язками рівняння$5(x-2)(x+3)=0$ є$x=2$ і$x=-3$. Ми можемо легко перевірити, що$5(x-2)(x+3)$ оцінюється при$x=2$ дає 0, а також при$x=-3$ дає 0.

б)$(5 x-4)(x-6)=0$

Зверніть увагу, що це рівняння вже в стандартній формі і враховано, і ми можемо безпосередньо застосувати властивість нульового продукту.

\[(5 x-4)=0 \text { or }(x-6)=0\nonumber\]

\[5 x-4=0 \text{ gives }5x = 4 \text{ and thus }x=\frac{4}{5}\nonumber\]

\[x − 6 = 0 \text{ gives } x = 6\nonumber\]

Отже, розв'язками рівняння$(5 x-4)(x-6)=0$ є$x=\frac{4}{5}$ і$x=6$.

Приклад 20.3

Розв'яжіть задані квадратичні рівняння:

а)$x^{2}-3 x-18=0$

Це квадратне рівняння в стандартній формі.

\[\begin{array} {ll} \text{Standard Form} & x^{2}-3 x-18=0 \\ \text{Factor} & \Longrightarrow(x-6)(x+3)=0 \\ \text{Zero-Product Property} & \Longrightarrow(x-6)=0 \text { or }(x+3)=0 \end{array}\nonumber\]

\[x − 6 = 0 \text{ gives } x = 6\nonumber\]

\[x + 3 = 0 \text{ gives } x = −3\nonumber\]

Так$x=6$ чи$x=-3$.

б)$x^{2}=81$

Це квадратне рівняння не в стандартній формі.

\[\begin{array} {ll} \text{Standard Form} & x^{2}-81=0 \\ \text{Factor} & \Longrightarrow x^{2}-(9)^{2}=0 \\ & \Longrightarrow(x-9)(x+9)=0 \\ \text{Zero-Product Property} & \Longrightarrow(x-9)=0 \text { or }(x+9)=0 \end{array}\nonumber\]

\[x − 9 = 0 \text{ gives } x = 9 \nonumber\]

\[x + 9 = 0 \text{ gives } x = −9 \nonumber\]

Рішення є$x=9$ і$x=-9$.

в)$3 x^{2}-27=0$

Це квадратне рівняння в стандартній формі.

\[\begin{array} {ll} \text{Standard Form} & 3 x^{2}-27=0 \\ \text{Factor} & \Longrightarrow 3 \cdot x^{2}-3 \cdot 9=0 \\ & \Longrightarrow 3\left(x^{2}-9\right)=0 \\ & \Longrightarrow 3\left(x^{2}-3^{2}\right)=0 \\ & \Longrightarrow 3(x-3)(x+3)=0 \\ \text{Zero-Product Property} & \Longrightarrow(x-3)=0 \text { or }(x+3)=0 \end{array}\nonumber\]

\[x − 3 = 0 \text{ gives }x = 3 \nonumber\]

\[x + 3 = 0 \text{ gives } x = −3 \nonumber\]

Рішення є$x=3$ і$x=-3$.

г)$x^{2}+5 x+4=0$

\[\begin{array} {ll} \text{Standard Form} & x^{2}+5 x+4=0 \\ \text{Factor} & \Longrightarrow(x+4)(x+1)=0 \\ \text{Zero-Product Property} & \Longrightarrow(x+4)=0 \text { or }(x+1)=0 \end{array}\nonumber\]

\[x + 4 = 0 \text{ gives } x = −4\nonumber\]

\[x + 1 = 0 \text{ gives } x= -1\nonumber\]

Так що якщо$x^{2}+5 x+4=0$ тоді$x=-4$ або$x=-1$.

д)$x^{2}=7 x$

\[\begin{array} {ll} \text{Standard Form} & x^{2}-7 x=0 \\ \text{Factor} & \Longrightarrow x \cdot x-7 \cdot x=0 \\ & \Longrightarrow x(x-7)=0 \\ \text{Zero-Product Property} & \Longrightarrow x=0 \text { or }(x-7)=0 \end{array}\nonumber\]

\[x=0 \text{ gives }x=0\nonumber\]

\[x-7=0 \text{ gives } x= 7\nonumber\]

Рішення є$x=0$ і$x=7$

f)$4 x^{2}+20 x=0$

\[\begin{array} {ll} \text{Standard Form} & 4 x^{2}+20 x=0 \\ \text{Factor} & \Longrightarrow 4 x \cdot x+4 x \cdot 5=0 \\ & \Longrightarrow 4 x(x+5)=0 \\ \text{Zero-Product Property} & \Longrightarrow 4 x=0 \text { or }(x+5)=0 \end{array}\nonumber\]

\[4x = 0 \text{ gives } \frac{4 x}{4}=\frac{0}{4} \text{ thus } x=0\nonumber\]

\[x + 5 = 0 \text{ gives } x = −5\nonumber\]

Рішення є$x=0$ і$x=-5$.

г)$4 x^{2}-25=0$

\[\begin{array} {ll} \text{Standard Form} & 4 x^{2}-25=0 \\ \text{Factor} & \Longrightarrow(2 x)^{2}-(5)^{2}=0 \\ & \Longrightarrow(2 x-5)(2 x+5)=0 \\ \text{Zero-Product Property} & \Longrightarrow(2 x-5)=0 \text { or }(2 x+5)=0 \end{array}\nonumber\]

\[2 x-5=0 \text{ gives } 2 x=5 \text{ thus } x=\frac{5}{2} \nonumber\]

\[2 x+5=0 \text{ gives } 2 x=-5 \text{ thus } x=\frac{-5}{2} \nonumber\]

Рішення є$x=\frac{5}{2}$ чи$x=-\frac{5}{2}$

ч)$3 x^{2}+7 x+2=0$

\[\begin{array} {ll} \text{Standard Form} & 3 x^{2}+7 x+2=0 \\ \text{Factor} & \Longrightarrow 3 x^{2}+6 x+x+2=0 \\ & \Longrightarrow 3 x \cdot x+3 x \cdot 2+x+2=0 \\ & \Longrightarrow 3 x(x+2)+(x+2)=0 \\ & \Longrightarrow(3 x+1)(x+2)=0 \\ \text{Zero-Product Property} & \Longrightarrow(3 x+1)=0 \text { or }(x+2)=0 \end{array}\nonumber\]

\[3 x+1=0 \text{ gives } 3 x=-1 \text{ thus } x=\frac{-1}{3} \nonumber\]

\[x+2=0 \text{ gives } x=-2 \nonumber\]

Рішення є$x=-\frac{1}{3}$ і$x=-2$.

i)$x^{2}=-2 x-1$

\[\begin{array} {ll} \text{Standard Form} & \Longrightarrow x^{2}+2 x+1=0 \\ \text{Factor} & \Longrightarrow(x+1)(x+1)=0 \\ \text{Zero-Product Property} & \Longrightarrow(x+1)=0 \text { or }(x+1)=0 \end{array}\nonumber\]

\[x+1=0 \text{ gives } x=-1 \nonumber\]

Оскільки обидва рішення однакові, ми говоримо, що у нас є подвійне рішення$x=-1$.

j)$2 x^{2}-32=0$

\[\begin{array} {ll} \text{Standard Form} & \Longrightarrow 2 x^{2}-32=0 \\ \text{Factor} & \\ \Longrightarrow 2 \cdot x^{2}-2 \cdot 16=0 & \Longrightarrow 2\left(x^{2}-16\right)=0 \\ & \Longrightarrow 2\left(x^{2}-4^{2}\right)=0 \\ & \Longrightarrow 2(x-4)(x+4)=0\\ & \Longrightarrow(x-4)(x+4)=0 \\ \text{Zero-Product Property} & \Longrightarrow(x-4)=0 \text { or }(x+4)=0 \end{array}\nonumber\]

\[x-4=0 \text{ gives } x=4 \nonumber\]

\[x+4=0 \text{ gives } x=-4 \nonumber\]

Рішення є$x=4$ і$x=-4$.

к)$3 x^{2}-3 x-6=0$

\[\begin{array} {ll} \text{Standard Form} & 3 x^{2}-3 x-6=0 \\ \text{Factor} & \Longrightarrow 3 \cdot x^{2}-3 \cdot x-3 \cdot 2=0 \\ & \Longrightarrow 3\left(x^{2}-x-2\right)=0 \\ & \Longrightarrow 3(x-2)(x+1)=0 \\ & \Longrightarrow(x-2)(x+1)=0 \\ \text{Zero-Product Property} & \Longrightarrow(x-2)=0 \text { or }(x+1)=0 \end{array}\nonumber\]

\[x-2=0 \text{ gives } x=2 \nonumber\]

\[x+1=0 \text{ gives } x=-1 \nonumber\]

Рішення є$x=2$ і$x=-1$.

Якщо прямокутник має площу 15 квадратних футів і його довжина на два фути менше його ширини, то які розміри прямокутника.

$x$Дозволяти представляти ширину. Тоді довжина дорівнює$x-2$. Площа, з одного боку, становить 15 квадратних футів, а з іншого боку$l \times w.$ це

\[15=x(x-2)\nonumber\]

Спочатку роздаємо, щоб отримати

\[15=x^{2}-2 x\nonumber\]

Тепер складаємо його в стандартному вигляді, віднімаючи 15 з обох сторін:

\[x^{2}-2 x-15=0\nonumber\]

Тепер ми враховуємо, щоб ми могли використовувати властивість нульового продукту:

\[(x-5)(x+3)=0\nonumber\]

Тоді$x-5=0$ або$x+3=0,$ який дає що$x=5$ або$x=-3 .$ Але$x$ це ширина прямокутника, і тому вона не може бути негативною. Єдиним рішенням цієї проблеми є$x=5$ (і$x-2=3$). Отже, розміри прямокутника складають 5 футів на 3 фути.

Розв'язування квадратних рівнянь виду$x^2 = A$

В особливому випадку, коли квадратне рівняння має форму$x^{2}=A$, ми можемо вдатися до короткого скорочення для його вирішення. Майте на увазі, що це коротке скорочення працює лише в цьому особливому випадку.

Спочатку зауважимо, що якщо$x^{2}=9$ потім, шляхом огляду, рішення 3 і -3 Ми бачимо, що загалом для вирішення$x^{2}=A,$ ми бачимо, що рішення є$x=\sqrt{A}$ і$x=-\sqrt{A}$.

Зверніть увагу, що якщо ми використовуємо метод факторингу, рівняння$x^{2}=A$ стає$x^{2}-A=0$ стандартною формою, а факторна форма рівняння - це те,$(x-$$\sqrt{A})(x+\sqrt{A})=0$ що дає розв'язки$x=\sqrt{A}$ і$x=-\sqrt{A}$.

Приклад 20.4

Використовуйте ярлик вище, щоб розв'язати задане спеціальне квадратне рівняння:

а)$x^{2}=100$

Крок 1. $\sqrt{100}=10$

Крок 2. Рішення є$x=10$ і$x=-10$

б)$x^{2}=72$

Крок 1. $\sqrt{72}=6 \sqrt{2}$

Крок 2. Рішення є$x=6 \sqrt{2}$ і$x=-6 \sqrt{2}$

в)$x^{2}-75=0$

Крок 1. $\sqrt{75}=5 \sqrt{3}$

Крок 2. Рішення є$x=5 \sqrt{3}$ і$x=-5 \sqrt{3}$

г) Площа квадрата становить 20 квадратних футів. Скільки триває кожна сторона?

$x$Дозволяти довжина кожної сторони. Тоді$x^{2}=20 .$ так$x=\sqrt{20}=2 \sqrt{5} .$ зверніть увагу, що це не може бути$x$,$-2 \sqrt{5}$ так як це довжина. Кожна сторона$2 \sqrt{5}$ футів.

Застосування до теореми Піфагора

Теорема Піфагора пов'язує довжини катетів прямокутного трикутника і гіпотенузи.

Теорема Піфагора: Якщо$a$ і$b$ є довжинами катетів прямокутного трикутника і$c$ є довжиною гіпотенузи (сторони, протилежної прямому куту), як показано на цьому малюнку,

$clipboard_e1f77e1e7cd745949914c10c1e8d26110.png$

потім

\[a^{2}+b^{2}=c^{2}\nonumber\]

Зауваження 20.5

У теоремі a і b взаємозамінні.

Приклад 20.6

Розглянемо наступний прямокутний трикутник.

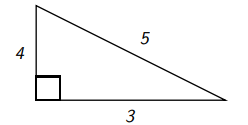
$clipboard_e65e0b01c47b834e234a8a192a855cb35.png$

Він задовольняє висновок теореми Піфагора з$3^{2}+4^{2}=5^{2}$ (перевірити його).

Зауваження 20.7

Не сприймайте пропорції трикутників, намальованих серйозно - те, що здається найкоротшою ногою, насправді може не бути. Ці малюнки - це лише мультфільми, які демонструють зв'язок між ногами, оскільки вони стосуються кутів.

Якщо ми знаємо будь-які дві сторони прямокутного трикутника, ми можемо знайти третю за допомогою теореми Піфагора. Ми розглянемо кілька прикладів.

Приклад 20.8

Знайти$x$ якщо

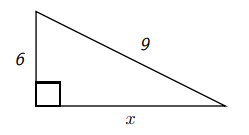
$clipboard_e3952fa2d3b58c01897395d588b5e8407.png$

За теоремою Піфагора (зазначаючи, що довжина гіпотенузи дорівнює 9 і так 81 належить з одного боку рівності)

\[x^{2}+6^{2}=9^{2} \text{, or equivalently ,} x^{2}+36=81 \nonumber\]

так що

\[x^{2}=81-36 \text{, or equivalently ,} x^{2}=45 \nonumber\]

Тепер, оскільки$x$ представляє довжину, вона позитивна, так що

\[x=\sqrt{45}=\sqrt{9 \cdot 5}=3 \sqrt{5}\nonumber\]

Приклад 20.9

Знайти$x$ наведену нижче картинку

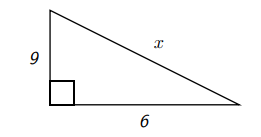
$clipboard_eff202c93472db9cc5d53f54484d96c9c.png$

За теоремою Піфагора (зазначаючи, що довжина гіпотенузи є$x$ і так$x^{2}$ належить з одного боку рівності)

\[6^{2}+9^{2}=x^{2} \text{, or equivalently ,} 36+81=x^{2} \nonumber\]

так що

\[ x^{2}=117 \nonumber\]

Тепер, оскільки$x$ представляє довжину, вона позитивна, так що

\[ x=\sqrt{117}=\sqrt{9 \cdot 13}=3 \sqrt{13} \nonumber\]

Приклад 20.10

Припустимо, ви повинні дістатися до вікна будинку зі сходами, щоб сходи зустрічалися з будинком 7 футів від землі. Припустимо також, що сходи повинні знаходитися на відстані 5 футів від підстави будинку. Скільки повинна бути сходи?

Ця інформація призводить до трикутника (не намальованого в масштабі):

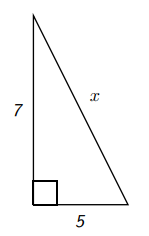
$clipboard_e1ae599c26ec45928604b92880c1074d7.png$

Так за теоремою Піфагора говорить:

\[ 5^{2}+7^{2}=x^{2} \nonumber\]

так що$x^{2}=74$. Тому сходи повинні бути довжиною$\sqrt{74}$ футів, що приблизно 8,6 футів завдовжки.

Проблема виходу

$clipboard_e9625f87f9a05b609d788f5dc66b0ed30.png$ Вирішити:$x^{2}-5 x=6$
Вирішити:$16 x^{2}=81$
Вирішити:$-24 x=10 x^{2}$
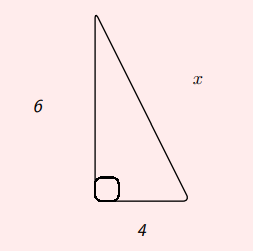
Вирішити for$x$ в заданому прямокутному трикутнику.