9.8: Ймовірність
- Page ID
- 59721
- Побудувати ймовірнісні моделі.
- Обчислити ймовірності однаково ймовірних результатів.
- Обчислити ймовірності об'єднання двох подій.
- Використовуйте правило доповнення, щоб знайти ймовірності.
- Обчислити ймовірність за допомогою теорії підрахунку.
Жителі південно-східних Сполучених Штатів занадто знайомі з діаграмами, відомими як моделі спагетті, такі як на малюнку\(\PageIndex{1}\). Вони поєднують сукупність даних про погоду, щоб передбачити найбільш ймовірний шлях урагану. Кожна кольорова лінія представляє один можливий шлях. Група химерних ліній може почати нагадувати пасма спагетті, звідси і назва. У цьому розділі ми дослідимо методи складання цих типів прогнозів.
Малюнок\(\PageIndex{1}\): Приклад «моделі спагетті», яку можна використовувати для прогнозування можливих шляхів тропічного шторму. 1
Побудова моделей ймовірності
Припустимо, ми розгортаємо шестигранний кубик числа. Прокатка числового куба є прикладом експерименту, або діяльності з спостережуваним результатом. Цифри на кубі є можливими результатами або результатами цього експерименту. Сукупність всіх можливих результатів експерименту називається зразковим простором експерименту. Простір зразка для цього експерименту є\(\{1,2,3,4,5,6 \}\). Подія - це будь-яка підмножина зразкового простору.
Імовірність події відома як ймовірність. Імовірність події pp - це число, яке завжди задовольняє\(0≤p≤1\), де\(0\) вказує на неможливу подію і\(1\) вказує на певну подію. Модель ймовірності - це математичний опис експерименту з перерахуванням усіх можливих результатів та пов'язаних з ними ймовірностей. Наприклад, якщо є\(1\%\) шанс виграти розіграш і\(99\%\) шанс програти розіграш, модель ймовірності буде виглядати так само, як Таблиця\(\PageIndex{1}\).
| Результат | ймовірність |
|---|---|
| Перемога в розіграші | 1% |
| Втрата розіграшу | 99% |
Сума ймовірностей, перерахованих в моделі ймовірності, повинна дорівнювати\(1\), або\(100\%\).
- Визначте кожен результат.
- Визначте загальну кількість можливих результатів.
- Порівняйте кожен результат із загальною кількістю можливих результатів.
Побудувати модель ймовірності для прокатки однієї, справедливої матриці, при цьому подія є числом, показаним на матриці.
Рішення
Почніть зі складання списку всіх можливих результатів для експерименту. Можливі результати - це числа, які можна згорнути:\(1\)\(2\),\(3\),\(4\),\(5\), і\(6\). Існує шість можливих результатів, які складають простір вибірки.
Призначте ймовірності кожному результату у вибірковому просторі, визначаючи відношення результату до кількості можливих результатів. Є одне з кожного з шести чисел на кубі, і немає підстав думати, що якась конкретна грань, швидше за все, з'явиться, ніж будь-яке інше, тому ймовірність прокатки будь-якого числа є\(16\).
| Результат | Рулон 1 | Рулон з 2 | Рулон з 3 | Рулон з 4 | Рулон з 5 | Рулон з 6 |
|---|---|---|---|---|---|---|
| Імовірність | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) |
Ні. Імовірності можуть бути виражені у вигляді дробів, десяткових знаків або відсотків. Імовірність завжди повинна бути числом між\(0\) і\(1\), включно\(0\) і\(1\).
Обчислення ймовірностей однаково ймовірних результатів
\(S\)Дозволяти бути зразком простору для експерименту. При дослідженні ймовірності подія є будь-якою підмножиною\(S\). Коли результати експерименту однаково вірогідні, ми можемо знайти ймовірність події, розділивши кількість результатів у події на загальну кількість результатів у\(S\). Припустимо, згорнутий числовий куб, і нас цікавить знаходження ймовірності події «прокатки числа менше або рівне 4». Є 4 можливі результати в події і 6 можливих результатів в\(S\), тому ймовірність події є\(\dfrac{4}{6}=\dfrac{2}{3}\).
Імовірність події\(E\) в експерименті з вибірковим простором\(S\) з однаково ймовірними результатами задається
\[P(E)=\dfrac{\text{number of elements in }E}{\text{number of elements in }S}=\dfrac{n(E)}{n(S)}\]
\(E\)є підмножиною\(S\), так що це завжди вірно, що\(0≤P(E)≤1\).
Прокочується кубик числа. Знайти ймовірність прокатки непарного числа.
Рішення
Подія «кочення непарного числа» містить три результати. Є\(6\) однаково ймовірні результати в просторі вибірки. Ділимо, щоб знайти ймовірність події.
\(P(E)=\dfrac{3}{6}=\dfrac{1}{2}\)
Прокочується кубик числа. Знайти ймовірність прокатки числа більше ніж\(2\).
- Відповідь
-
\(\dfrac{2}{3}\)
Обчислення ймовірності об'єднання двох подій
Ми часто зацікавлені в тому, щоб знайти ймовірність того, що відбувається одна з декількох подій. Припустимо, ми граємо в карткову гру, і ми виграємо, якщо наступна намальована карта - це або серце, або король. Нам було б цікаво знайти ймовірність того, що наступна карта буде серцем або королем. Об'єднання двох подій\(E\) і\(F\), написано\(E\cup F\), - це подія, яка відбувається, якщо відбувається будь-яка або обидві події.
\[P(E\cup F)=P(E)+P(F)−P(E\cap F)\]
Припустимо, прядильник на малюнку\(\PageIndex{2}\) закручений. Ми хочемо, щоб знайти ймовірність спінінг помаранчевий або спінінг a\(b\).
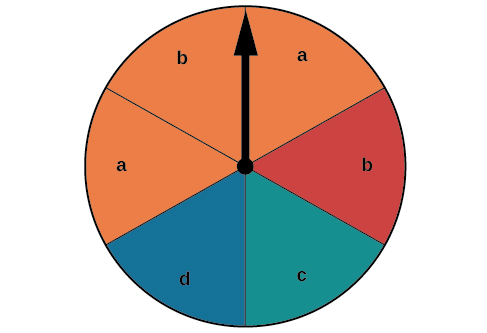
Малюнок\(\PageIndex{2}\): Кругова діаграма з шістьма варіантами.
Є всього\(6\) секцій, і\(3\) з них помаранчеві. Так що ймовірність закрутити помаранчевий є\(\dfrac{3}{6}=\dfrac{1}{2}\). Існує загальна кількість\(6\) розділів, і\(2\) з них є\(b\). Так що ймовірність спінінгу a\(b\) є\(\dfrac{2}{6}=\dfrac{1}{3}\). Якби ми додали ці дві ймовірності, ми б вважали сектор, який є одночасно помаранчевим і\(b\) двічі. Щоб знайти ймовірність закрутки апельсина або а\(b\), нам потрібно відняти ймовірність того, що сектор одночасно помаранчевий і має\(b\).
\(\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{6}=\dfrac{2}{3}\)
Імовірність закрутки оранжевого або а\(b\) є\(\dfrac{2}{3}\).
Імовірність об'єднання двох подій\(E\) і\(F\) (записаних\(E\cup F\)) дорівнює сумі ймовірності\(E\) і ймовірності\(F\) мінус ймовірності\(E\) і\(F\) відбуваються разом (що називається перетином\(E\) і\(F\) і пишеться як\(E\cap F\)).
\[P(E\cup F)=P(E)+P(F)−P(E\cap F)\]
З стандартної колоди витягується карта. Знайдіть ймовірність намалювання серця або а\(7\).
Рішення
Стандартна колода містить рівну кількість сердець, діамантів, треф і пік. Так що ймовірність намалювати серце є\(\dfrac{1}{4}\). Їх чотири\(7s\) в стандартній колоді, а всього\(52\) карт. Так що ймовірність малювання а\(7\) є\(\dfrac{1}{13}\).
Єдина карта в колоді, яка є і серцем, і\(7\) є\(7\) сердець, тому ймовірність намалювати і серце, і\(7\) є\(\dfrac{1}{52}\). Підставляємо\(P(H)=\dfrac{1}{4}\)\(P(7)=\dfrac{1}{13}\), і\(P(H\cap 7)=\dfrac{1}{52}\) в формулу.
\[\begin{align*} P(E\cup F) &=P(E)+P(F)−P(E\cap F) \\[4pt] &=\dfrac{1}{4}+\dfrac{1}{13}−\dfrac{1}{52} \\[4pt] &=\dfrac{4}{13} \end{align*}\]
Імовірність намалювати серце або\(7\) є\(\dfrac{4}{13}\).
З стандартної колоди витягується карта. Знайдіть ймовірність намалювати червону картку або туза.
- Відповідь
-
\(\dfrac{7}{13}\)
Обчислення ймовірності взаємовиключних подій
Припустимо, спиннер на малюнку\(\PageIndex{2}\) закручується знову, але на цей раз нас цікавить ймовірність закрутки апельсина або а\(d\). Немає секторів, які є помаранчевими і містять a\(d\), тому ці дві події не мають спільних результатів. Кажуть, що події є взаємовиключними подіями, коли вони не мають спільних результатів. Оскільки перекриття немає, віднімати нічого, тому загальна формула
\[P(E\cap F)=P(E)+P(F)\]
Зверніть увагу, що при взаємовиключних подіях перетин\(E\) і\(F\) є порожнім набором. Імовірність спінінгу апельсина є\(\dfrac{3}{6}=\dfrac{1}{2}\) і ймовірність спінінгу а\(d\) є\(\dfrac{1}{6}\). Ми можемо знайти ймовірність обертання апельсина або\(d\) просто, додавши дві ймовірності.
\[\begin{align*} P(E\cap F)&=P(E)+P(F) \\[4pt] &=\dfrac{1}{2}+\dfrac{1}{6} \\ &=\dfrac{2}{3} \end{align*}\]
Імовірність закрутки апельсина або а\(d\) є\(\dfrac{2}{3}\).
Імовірність об'єднання двох взаємовиключних подій\(E\) і\(F\) задається
\[P(E\cap F)=P(E)+P(F)\]
- Визначте загальну кількість результатів для першої події.
- Знайдіть ймовірність першої події.
- Визначте загальну кількість результатів для другої події.
- Знайти ймовірність другої події.
- Додайте ймовірності.
З стандартної колоди витягується карта. Знайдіть ймовірність намалювати серце або лопату.
Рішення
Події «малювання серця» і «малювання лопати» є взаємовиключними, оскільки не можуть відбуватися одночасно. Імовірність намалювати серце є\(\dfrac{1}{4}\), і ймовірність намалювати лопата теж\(\dfrac{1}{4}\), тому ймовірність намалювати серце або лопата дорівнює
\(\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2}\)
З стандартної колоди витягується карта. Знайдіть ймовірність намалювати туза або короля.
- Відповідь
-
\(\dfrac{2}{13}\)
Використання правила доповнення для обчислення ймовірностей
Ми обговорили, як розрахувати ймовірність того, що трапиться якась подія. Іноді нам цікаво знайти ймовірність того, що якась подія не відбудеться. Доповненням події\(E\), що позначається\(E′\), є сукупність результатів у вибірковому просторі, яких немає в\(E\). Наприклад, припустимо, нас цікавить ймовірність того, що кінь програє забіг. Якщо подією\(W\) є кінь, яка виграла гонку, то доповненням події\(W\) є кінь, що програє гонку.
Щоб знайти ймовірність того, що кінь програє забіг, потрібно використовувати той факт, що сума всіх ймовірностей в моделі ймовірності повинна бути\(1\).
\[P(E′)=1−P(E)\]
Імовірність виграшу коня, що додається до ймовірності програшу коня, повинна дорівнювати\(1\). Тому, якщо ймовірність перемоги коня в гонці є\(\dfrac{1}{9}\), ймовірність того, що кінь програє гонку, просто
\(1−\dfrac{1}{9}=\dfrac{8}{9}\)
Імовірність того, що доповнення події відбудеться, дається
\[P(E′)=1−P(E)\]
Розкочуються два шестигранних кубика цифри.
- Знайти ймовірність того, що сума згорнутих чисел менше або дорівнює\(3\).
- Знайти ймовірність того, що сума згорнутих чисел більше\(3\).
Рішення
Насамперед необхідно визначити простір вибірки, який складається з усіх можливих результатів. Є два кубики чисел, і кожен кубик числа має шість можливих результатів. Використовуючи принцип множення, ми знаходимо, що є\(6×6\), або\(36\) загальні можливі результати. Так, наприклад,\(1-1\) являє собою\(1\) згорнутий на кожному номері куб.
| \(1-1\) | \(1-2\) | \(1-3\) | \(1-4\) | \(1-5\) | \(1-6\) |
| \(2-1\) | \(2-2\) | \(2-3\) | \(2-4\) | \(2-5\) | \(2-6\) |
| \(3-1\) | \(3-2\) | \(3-3\) | \(3-4\) | \(3-5\) | \(3-6\) |
| \(4-1\) | \(4-2\) | \(4-3\) | \(4-4\) | \(4-5\) | \(4-6\) |
| \(5-1\) | \(5-2\) | \(5-3\) | \(5-4\) | \(5-5\) | \(5-6\) |
| \(6-1\) | \(6-2\) | \(6-3\) | \(6-4\) | \(6-5\) | \(6-6\) |
- Нам потрібно порахувати кількість способів згорнути суму\(3\) або менше. Вони включали б такі результати:\(1-1\),\(1-2\), і\(2-1\). Таким чином, існує всього три способи згорнути суму\(3\) або менше. Імовірність
\(\dfrac{3}{36}=\dfrac{1}{12}\)
- Замість того, щоб перераховувати всі можливості, ми можемо використовувати правило доповнення. Оскільки ми вже знайшли ймовірність доповнення цієї події, ми можемо просто відняти цю ймовірність,\(1\) щоб знайти ймовірність того, що сума згорнутих чисел більше\(3\).
\[\begin{align*} P(E')&=1-P(E)\\ &=1-\dfrac{1}{12}\\ &=\dfrac{11}{12} \end{align*}\]
Скачуються два кубика числа. Скористайтеся правилом доповнення, щоб знайти ймовірність того, що сума менше\(10\).
- Відповідь
-
\(\dfrac{5}{6}\)
Обчислення ймовірності за допомогою теорії підрахунку
Багато цікавих проблем ймовірності включають принципи підрахунку, перестановки та комбінації. У цих задачах ми будемо використовувати перестановки та комбінації, щоб знайти кількість елементів у подіях та просторах вибірки. Ці проблеми можуть бути складними, але їх можна полегшити, розбивши їх на менші проблеми підрахунку.
Припустимо, наприклад, що магазин має\(8\) стільникові телефони, і що\(3\) з них несправні. Ми можемо знайти ймовірність того, що пара, купуючи\(2\) телефони, отримує\(2\) телефони, які не є дефектними. Щоб вирішити цю проблему, нам потрібно прорахувати всі способи вибору\(2\) телефонів, які не браковані, а також всі способи вибору\(2\) телефонів. Є\(5\) телефони, які не є несправними, тому існують\(C(5,2)\) способи вибору\(2\) телефонів, які не є несправними. Є\(8\) телефони, тому існують\(C(8,2)\) способи вибору\(2\) телефонів. Імовірність вибору\(2\) телефонів, які не браковані, становить:
\[ \begin{align*} \dfrac{\text{ways to select 2 phones that are not defective}}{\text{ways to select 2 phones}}&=\dfrac{C(5,2)}{C(8,2)} \\[4pt] &=\dfrac{10}{28} \\[4pt] &=\dfrac{5}{14} \end{align*}\]
Дитина випадковим чином вибирає\(5\) іграшки з кошика, що містить\(3\) зайчиків,\(5\) собак і\(6\) ведмедів.
- Знайдіть ймовірність того, що вибираються тільки ведмеді.
- Знайдіть ймовірність того, що\(2\) ведмеді і\(3\) собаки обрані.
- Знайдіть ймовірність того, що вибрані хоча б\(2\) собаки.
Рішення
- Потрібно порахувати кількість способів вибору тільки ведмедів і загальну кількість можливих способів вибору\(5\) іграшок. Є\(6\) ведмеді, тому є\(C(6,5)\) способи вибору\(5\) ведмедів. Є\(14\) іграшки, тому є\(C(14,5)\) способи вибору будь-яких\(5\) іграшок.
\(\dfrac{C(6,5)}{C(14,5)}=\dfrac{6}{2,002}=\dfrac{3}{1,001}\)
- Потрібно порахувати кількість способів вибору\(2\) ведмедів і\(3\) собак і загальну кількість можливих способів вибору\(5\) іграшок. Є\(6\) ведмеді, тому є\(C(6,2)\) способи вибору\(2\) ведмедів. Є\(5\) собаки, тому є\(C(5,3)\) способи вибору\(3\) собак. Оскільки ми вибираємо одночасно і ведмедів, і собак, ми будемо використовувати Принцип множення. Є\(C(6,2)⋅C(5,3)\) способи вибору\(2\) ведмедів і\(3\) собак. Ми можемо використовувати цей результат, щоб знайти ймовірність.
\(\dfrac{C(6,2)C(5,3)}{C(14,5)}=\dfrac{15⋅10}{2,002}=\dfrac{75}{1,001}\)
- Часто найпростіше вирішити «хоча б» проблеми за допомогою правила доповнення. Почнемо з того, що знайдемо ймовірність того, що вибрано менше\(2\) собак. Якщо вибирається менше\(2\) собак, то або собак не можна було вибрати, або\(1\) собаку можна вибрати.
Коли жодних собак не вибирають, всі\(5\) іграшки походять від\(9\) іграшок, які не є собаками. Існують\(C(9,5)\) способи вибору іграшок з\(9\) іграшок, які не є собаками. Так як є\(14\) іграшки, є\(C(14,5)\) способи вибрати\(5\) іграшки з усіх іграшок.
\(\dfrac{C(9,5)}{C(14,5)}=\dfrac{63}{1,001}\)
Якщо там обрана\(1\) собака, то\(4\) іграшки повинні виходити з\(9\) іграшок, які не є собаками, і\(1\) повинні виходити від\(5\) собак. Оскільки ми вибираємо одночасно і собак, і інші іграшки, ми будемо використовувати Принцип множення. Є\(C(5,1)⋅C(9,4)\) способи вибрати\(1\) собаку та\(1\) іншу іграшку.
\(\dfrac{C(5,1)C(9,4)}{C(14,5)}=\dfrac{5⋅126}{2,002}=\dfrac{315}{1,001}\)
Оскільки ці події не відбуватимуться разом і тому є взаємовиключними, ми додаємо ймовірності знайти ймовірність того, що вибирається менше, ніж\(2\) собак.
\(\dfrac{63}{1,001}+\dfrac{315}{1,001}=\dfrac{378}{1,001}\)
Потім ми віднімаємо цю ймовірність,\(1\) щоб знайти ймовірність того, що принаймні\(2\) собаки обрані.
\(1−\dfrac{378}{1,001}=\dfrac{623}{1,001}\)
Дитина випадковим чином вибирає\(3\) гумбали з контейнера, що тримає\(4\) фіолетові гумболи,\(8\) жовті гумболи та\(2\) зелені гумкулі.
- Знайдіть ймовірність того, що всі вибрані\(3\) гумбали фіолетові.
- Знайдіть ймовірність того, що жодних жовтих гумбал не вибрано.
- Знайдіть ймовірність того, що обраний хоча б\(1\) жовтий гумбал.
- Відповідь
-
\(\dfrac{1}{91}\)
- Відповідь
-
\(\dfrac{5}{91}\)
- Відповідь
-
\(\dfrac{86}{91}\)
Отримайте доступ до цих онлайн-ресурсів для додаткової інструкції та практики з ймовірністю.
Відвідайте цей веб-сайт для додаткових питань практики від Learningpod.
Ключові рівняння
| ймовірність події з однаково ймовірними наслідками | \(P(E)=\dfrac{n(E)}{n(S)}\) |
| ймовірність об'єднання двох подій | \(P(E\cup F)=P(E)+P(F)−P(E\cap F)\) |
| ймовірність об'єднання взаємовиключних подій | \(P(E\cup F)=P(E)+P(F)\) |
| ймовірність доповнення події | \(P(E')=1−P(E)\) |
Ключові концепції
- Імовірність - це завжди число між\(0\) і\(1\), де\(0\) означає, що подія неможлива і\(1\) означає, що подія є певною.
- Імовірності в моделі ймовірності повинні сумувати до\(1\). Див\(\PageIndex{1}\). Приклад.
- Коли результати експерименту однаково вірогідні, ми можемо знайти ймовірність події, розділивши кількість результатів події на загальну кількість результатів у вибірковому просторі для експерименту. Див\(\PageIndex{2}\). Приклад.
- Щоб знайти ймовірність об'єднання двох подій, складемо ймовірності двох подій і віднімаємо ймовірність того, що обидві події відбуваються одночасно. Див\(\PageIndex{3}\). Приклад.
- Щоб знайти ймовірність об'єднання двох взаємовиключних подій, додамо ймовірності кожної з подій. Див\(\PageIndex{4}\). Приклад.
- Імовірність доповнення події - це різниця між\(1\) і ймовірністю того, що подія відбувається. Див\(\PageIndex{5}\). Приклад.
- У деяких задачах ймовірності нам потрібно використовувати перестановки та комбінації, щоб знайти кількість елементів у подіях та просторах вибірки. Див\(\PageIndex{6}\). Приклад.
