7.6: Матриці та матричні операції
- Page ID
- 59751
- Знайти суму і різницю двох матриць.
- Знайти скалярні кратні матриці.
- Знайдіть добуток двох матриць.
Дві футбольні команди клубу, Wildcats і грязьові кішки, сподіваються отримати нове обладнання для майбутнього сезону. Таблиця\(\PageIndex{1}\) показує потреби обох команд.
| Дикі коти | Бруд Кішки | |
|---|---|---|
| Цілі | 6 | 10 |
| Кульки | 30 | 24 |
| Трикотажні вироби | 14 | 20 |
Мета коштує\($300\); м'яч коштує\($10\); і трикотаж коштує\($30\). Як ми можемо знайти загальну вартість обладнання, необхідного для кожної команди? У цьому розділі ми відкриваємо метод, за допомогою якого дані в таблиці футбольного обладнання можуть відображатися та використовуватися для обчислення іншої інформації. Тоді ми зможемо розрахувати вартість обладнання.

Пошук суми та різниці двох матриць
Для вирішення такої задачі, як описана для футбольних команд, ми можемо використовувати матрицю, яка представляє собою прямокутний масив чисел. Рядок в матриці - це набір чисел, які вирівняні по горизонталі. Стовпець в матриці являє собою набір чисел, які вирівняні по вертикалі. Кожне число є записом, який іноді називають елементом, матриці. Матриці (множина) укладені в [] або () і зазвичай називаються великими літерами. Наприклад, три матриці названі\(A\)\(B\), і\(C\) наведені нижче.
\[ \begin{align*} A&=\begin{bmatrix} 1& 2 \\ 3 & 4 \\ \end{bmatrix} \\[4pt] B &=\begin{bmatrix} 1 & 2 & 7 \\ 0 & -5 & 6 \\ 7 & 8 & 2 \end{bmatrix} \\[4pt] C &=\begin{bmatrix} -1 & 3 \\ 0 & 2 \\ 3 & 1 \end{bmatrix} \end{align*}\]
Матрицю часто називають її розміром або розмірами:\(m×n\) із зазначенням\(m\) рядків і\(n\) стовпців. Записи матриці визначаються спочатку рядком, а потім стовпчиком. Наприклад, щоб знайти запис у матриці,\(A\) визначеній як\(a_{ij}\), ми шукаємо запис у рядку\(i\), стовпці\(j\). У матриці\(A\), показаної нижче, запис у рядку\(2\), стовпець\(3\) є\(a_{23}\).
\[A=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33} \end{bmatrix} \nonumber\]
- Квадратна матриця - це матриця з розмірами\(n × n\), тобто вона має таку ж кількість рядків, як і стовпці. Наведена вище\(3×3\) матриця є прикладом квадратної матриці.
- Матриця рядків - це матриця, що складається з одного рядка з розмірами\(1 × n\). \[\begin{bmatrix} a_{11} & a_{12} & a_{13} \end{bmatrix} \nonumber\]
- Матриця стовпців - це матриця, що складається з одного стовпця з розмірами\(m × 1\). \[\begin{bmatrix} a_{11} \\ a_{21} \\a_{31} \end{bmatrix} \nonumber\]
Матриця може бути використана для представлення системи рівнянь. У цих випадках числа представляють собою коефіцієнти змінних в системі. Матриці часто полегшують рішення систем рівнянь, оскільки вони не обтяжені змінними. Ми будемо досліджувати цю ідею далі в наступному розділі, але спочатку розглянемо основні матричні операції.
Матриця - це прямокутний масив чисел, який зазвичай іменується великою літерою:\(A\)\(B\)\(C\),, і так далі. Кожен запис у матриці називається таким\(a_{ij}\), який\(i\) представляє рядок і\(j\) представляє стовпець. Матриці часто називають за своїми розмірами:\(m × n\) із зазначенням\(m\) рядків і\(n\) стовпців.
Задана матриця\(A\):
- Які розміри матриці\(A\)?
- Які записи в\(a_{31}\) і\(a_{22}\)?
\[A=\begin{bmatrix} 2 & 1 & 0\\2 & 4 & 7\\3 & 1 & −2 \end{bmatrix} \nonumber\]
Рішення
- Розміри полягають у\(3 \times 3\) тому, що є три рядки та три стовпці.
- Запис\(a_{31}\) - це число в рядку 3, стовпець 1, який є\(3\). Запис\(a_{22}\) - це число в рядку 2, стовпець 2, який є\(4\). Пам'ятайте, спочатку йде рядок, потім стовпчик.
Додавання та віднімання матриць
Ми використовуємо матриці для перерахування даних або представлення систем. Оскільки записи є числами, ми можемо виконувати операції над матрицями. Ми додаємо або віднімаємо матриці шляхом додавання або віднімання відповідних записів. Для цього записи повинні відповідати. Тому додавання і віднімання матриць можливо тільки тоді, коли матриці мають однакові розміри. Ми можемо додати або відняти\(3 \times 3\) матрицю та іншу\(3 \times 3\) матрицю, але ми не можемо додати або відняти\(2 \times 3\) матрицю та\(3 \times 3\) матрицю, оскільки деякі записи в одній матриці не матимуть відповідного запису в іншій матриці.
Задані матриці\(A\) та\(B\) подібні розміри, додавання та віднімання\(A\) і\(B\) дасть матрицю\(C\) або матрицю\(D\) однакової розмірності.
\[A+B=C\]
такий, що\(a_{ij}+b_{ij}=c_{ij}\)
\[A−B=D\]
такий, що\(a_{ij}−b_{ij}=d_{ij}\)
Додавання матриці є комутативним.
\[A+B=B+A\]
Він також асоціативний.
\[(A+B)+C=A+(B+C)\]
Знайти суму\(A\) і\(B\), задану
\[A=\begin{bmatrix}a & b\\c & d \end{bmatrix} \nonumber\]
і
\[B=\begin{bmatrix}e & f\\g & h\end{bmatrix} \nonumber\]
Рішення
Додайте відповідні записи.
\[\begin{align} A+B &=\begin{bmatrix}a & b\\c & d\end{bmatrix}+\begin{bmatrix}e & f\\g & h\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}a+e & b+f\\c+g & d+h \end{bmatrix} \nonumber \end{align} \nonumber\]
Знайти суму\(A\) і\(B\).
\[A=\begin{bmatrix}4 &1\\3 & 2 \end{bmatrix} \nonumber\]
і
\[B=\begin{bmatrix}5 & 9\\0 & 7\end{bmatrix} \nonumber\]
Рішення
Додайте відповідні записи. Додайте запис у рядку 1, стовпці 1\(a_{11}\), матриці\(A\) до запису в рядку 1, стовпці 1\(b_{11}\), of\(B\). Продовжуйте роботу з шаблоном, доки не будуть додані всі записи.
\[\begin{align} A+B &=\begin{bmatrix}4&1\\3 &2\end{bmatrix}+\begin{bmatrix}5&9\\0&7\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}4+5&1+9\\3+0&2+7\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}9&10\\3&9\end{bmatrix} \nonumber \end{align} \nonumber\]
Знайдіть різницю\(A\) і\(B\).
\(A=\begin{bmatrix}−2&3\\0&1\end{bmatrix}\)і\(B=\begin{bmatrix}8&1\\5&4\end{bmatrix}\)
Рішення
Віднімаємо відповідні записи кожної матриці.
\[\begin{align} A−B &=\begin{bmatrix}−2&3\\0&1\end{bmatrix}−\begin{bmatrix}8&1\\5&4\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}−2−8&3−1\\0−5&1−4\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}−10&2\\−5&−3\end{bmatrix} \nonumber \end{align} \nonumber\]
Дано\(A\) і\(B\):
- Знайти суму.
- Знайдіть різницю.
\[A=\begin{bmatrix}2&−10&−2\\14&12&10\\4&−2&2\end{bmatrix} \nonumber\]
і
\[B=\begin{bmatrix}6&10&−2\\0&−12&−4\\−5&2&−2\end{bmatrix} \nonumber\]
Рішення
- Додайте відповідні записи.
\[\begin{align} A+B & =\begin{bmatrix} 2& −10& −2\\14 & 12 & 10\\4 & −2 & 2\end{bmatrix}+\begin{bmatrix}6 & 10 & −2\\0 & −12 & −4\\−5 & 2 & −2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}2+6 & −10+10 & −2−2\\14+0 & 12−12 & 10−4\\4−5 & −2+2 & 2−2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix} 8 & 0 & −4\\14 & 0 & 6\\−1 & 0 & 0\end{bmatrix} \nonumber \end{align} \nonumber\]
- Відніміть відповідні записи.
\[\begin{align} A−B &=\begin{bmatrix}2&−10&−2\\14&12&10\\4&−2&2\end{bmatrix}−\begin{bmatrix}6&10&−2\\0&−12&−4\\−5&2&−2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}2−6 & −10−10 & −2+2\\14−0 & 12+12 & 10+4\\4+5 & −2−2 & 2+2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−4 & −20 & 0\\14 & 24 & 14\\9 & −4 & 4\end{bmatrix} \nonumber \end{align} \nonumber\]
Додати матрицю\(A\) і матрицю\(B\).
\[A=\begin{bmatrix}2&6\\1&0\\1&−3\end{bmatrix} \nonumber\]
і
\[B=\begin{bmatrix}3&−2\\1&5\\−4&3\end{bmatrix} \nonumber\]
- Відповідь
-
\[\begin{align} A+B&=\begin{bmatrix}2&6\\ 1 &0\\1&−3\end{bmatrix}+\begin{bmatrix} 3&-2 \\1&5 \\-4&3\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}2+3&6+(−2)\\1+1&0+5\\1+(-4)&−3+3\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}5&4\\2&5\\-3&0\end{bmatrix} \nonumber \end{align} \nonumber\]
Пошук скалярних кратних матриці
Крім додавання і віднімання цілих матриць, існує багато ситуацій, в яких нам потрібно помножити матрицю на константу, яка називається скаляром. Нагадаємо, що скаляр - це дійсна числова величина, яка має величину, але не напрямок. Наприклад, час, температура і відстань - це скалярні величини. Процес скалярного множення передбачає множення кожного запису в матриці на скаляр. Скалярним кратним є будь-який запис матриці, що є результатом скалярного множення.
Розглянемо реальний сценарій, в якому університет повинен додати до свого інвентарю комп'ютерів, комп'ютерних столів та стільців у двох лабораторіях кампусу через збільшення зарахування. За їхніми\(15%\) оцінками, в обох лабораторіях потрібно більше обладнання. Поточний інвентар школи відображається в табл\(\PageIndex{2}\).
| Лабораторія А | Лабораторія B | |
|---|---|---|
| Комп'ютери | 15 | 27 |
| Комп'ютерні столи | 16 | 34 |
| Стільці | 16 | 34 |
Конвертуючи дані в матрицю, ми маємо
\[C_{2013}=\begin{bmatrix}15 & 27\\16&34\\16&34\end{bmatrix} \nonumber\]
Щоб розрахувати, скільки буде потрібно комп'ютерної техніки, множимо всі записи в матриці\(C\) на\(0.15\).
\[(0.15)C_{2013}=\begin{bmatrix}(0.15)15&(0.15)27\\(0.15)16&(0.15)34\\(0.15)16 &(0.15)34\end{bmatrix}=\begin{bmatrix}2.25 &4.05\\2.4&5.1\\2.4&5.1\end{bmatrix} \nonumber\]
Ми повинні округлити до наступного цілого числа, тому кількість нового обладнання, необхідного
\[\begin{bmatrix}3&5\\3&6\\3&6\end{bmatrix} \nonumber\]
Додавши дві матриці, як показано нижче, ми бачимо нові суми запасів.
\[\begin{bmatrix}15&27\\16&34\\16&34\end{bmatrix}+\begin{bmatrix}3&5\\3&6\\3&6\end{bmatrix}=\begin{bmatrix}18&32\\19&40\\19&40\end{bmatrix} \nonumber\]
Це означає
\[C_{2014}=\begin{bmatrix}18&32\\19&40\\19&40\end{bmatrix} \nonumber\]
Таким чином, лабораторія А матиме\(18\) комп'ютери,\(19\) комп'ютерні столи та\(19\) стільці; Lab B матиме\(32\) комп'ютери,\(40\) комп'ютерні столи та\(40\) стільці.
Скалярне множення передбачає знаходження добутку константи на кожен запис в матриці. Враховується
\[A=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix} \nonumber\]
\(cA\)скалярне кратне
\[cA=c\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix} \nonumber\]
\[=\begin{bmatrix}ca_{11}&ca_{12}\\ca_{21}&ca_{22}\end{bmatrix} \nonumber\]
Скалярне множення є розподільним. Для матриць\(A\)\(B\), і\(C\) зі скалярами\(a\) і\(b\),
\[a(A+B)=aA+aB\]
\[(a+b)A=aA+bA\]
Помножте матрицю\(A\) на скаляр\(3\).
\[A=\begin{bmatrix}8&1\\5&4\end{bmatrix} \nonumber\]
Рішення
Помножте кожен запис\(A\) на скаляр\(3\).
\[ \begin{align} 3A&=3\begin{bmatrix}8&1\\5&4\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}3⋅8&3⋅1\\3⋅5&3⋅4\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}24&3\\15&12\end{bmatrix} \nonumber \end{align} \nonumber\]
Задана матриця\(B\), знайти\(−2B\) де
\[B=\begin{bmatrix}4&1\\3&2\end{bmatrix} \nonumber\]
- Відповідь
-
\[−2B=\begin{bmatrix}−8&−2\\−6&−4\end{bmatrix} \nonumber\]
Знайти суму\(3A+2B\).
\[A=\begin{bmatrix}1&−2&0\\0&−1&2\\4&3&−6\end{bmatrix} \nonumber\]
і
\[B=\begin{bmatrix}−1&2&1\\0&−3&2\\0&1&−4\end{bmatrix} \nonumber\]
Рішення
Спочатку знайдіть\(3A\), потім\(2B\).
\[ \begin{align} 3A&=\begin{bmatrix}3⋅1&3(−2)&3⋅0\\3⋅0&3(−1)&3⋅2\\3⋅4&3⋅3&3(−6)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}3&−6&0\\0&−3&6\\12&9&−18\end{bmatrix}\nonumber \end{align} \nonumber\]
\[ \begin{align} 2B&=\begin{bmatrix}2(−1)&2⋅2&2⋅1\\2⋅0&2(−3)&2⋅2\\2⋅0&2⋅1&2(−4)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−2&4&2\\0&−6&4\\0&2&−8\end{bmatrix}\nonumber \end{align} \nonumber\]
Тепер додайте\(3A+2B\).
\[ \begin{align} 3A+2B&=\begin{bmatrix}3&−6&0\\0&−3&6\\12&9&−18\end{bmatrix}+\begin{bmatrix}−2&4&2\\0&−6&4\\0&2&−8\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}3−2&−6+4&0+2\\0+0&−3−6&6+4\\12+0&9+2&−18−8\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}1& −2&2\\0&−9&10\\12&11&−26\end{bmatrix} \nonumber \end{align} \nonumber\]
Пошук добутку двох матриць
Крім множення матриці на скаляр, ми можемо помножити дві матриці. Знайти добуток двох матриць можливо тільки тоді, коли внутрішні розміри однакові, що означає, що кількість стовпців першої матриці дорівнює числу рядків другої матриці. Якщо\(A\) є\(m × r\) матрицею і\(B\) є\(r × n\) матрицею, то матриця добутку\(AB\) -\(m × n\) матриця. Наприклад, продукт\(AB\) можливий, оскільки кількість стовпців у\(A\) збігається з кількістю рядків у\(B\). Якщо внутрішні розміри не збігаються, виріб не визначається.
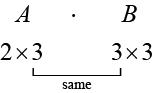
Ми множимо записи\(A\) з записами\(B\) за певною схемою, як зазначено нижче. Процес множення матриці стає зрозумілішим при роботі задачі з дійсними числами.
Щоб отримати записи в\(i\) рядку\(AB\), ми множимо записи в\(i\) рядку\(A\) на стовпчик\(j\)\(B\) і додаємо. Наприклад,\(A\) наведені матриці і\(B\), де розміри\(A\) є\(2 \times 3\) і розміри\(B\) є\(3 \times 3\), добутком\(AB\) буде\(2 \times 3\) матриця.
\[A=\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\end{bmatrix} \nonumber \]
і
\[B=\begin{bmatrix}b_{11}&b_{12}&b_{13}\\b_{21}&b_{22}&b_{23}\\b_{31}&b_{32}&b_{33}\end{bmatrix} \nonumber\]
Множимо і додаємо наступним чином, щоб отримати перший запис матриці добутку\(AB\).
- Щоб отримати запис у рядку 1, стовпці 1\(AB\), помножте перший рядок\(A\) на перший стовпець в\(B\), і додайте.
\[\begin{bmatrix}a_{11}&a_{12}&a_{13}\end{bmatrix} ⋅\begin{bmatrix}b_{11}\\b_{21}\\b_{31}\end{bmatrix}=a_{11}⋅b_{11}+a_{12}⋅b_{21}+a_{13}⋅b_{31} \nonumber \]
- Для отримання запису в рядку 1, стовпці 2\(AB\), помножте перший ряд\(A\) на другий стовпчик в\(B\), і додайте.
\[\begin{bmatrix}a_{11}&a_{12}&a_{13}\end{bmatrix} ⋅\begin{bmatrix}b_{12}\\b_{22}\\b_{32}\end{bmatrix}=a_{11}⋅b_{12}+a_{12}⋅b_{22}+a_{13}⋅b_{32} \nonumber \]
- Для отримання запису в рядку 1, стовпці 3\(AB\), помножте перший ряд\(A\) на третій стовпчик в\(B\), і додайте.
\[\begin{bmatrix}a_{11}&a_{12}&a_{13}\end{bmatrix} ⋅\begin{bmatrix}b_{13}\\b_{23}\\b_{33}\end{bmatrix}=a_{11}⋅b_{13}+a_{12}⋅b_{23}+a_{13}⋅b_{33} \nonumber \]
Так само чинимо до отримання другого ряду\(AB\). Іншими словами, рядок 2\(A\) разів стовпчик 1 з\(B\); рядок 2\(A\) разів стовпчик 2\(B\); рядок 2\(A\) разів стовпчик 3 з\(B\). По завершенню матриця продукту буде
\[AB=\begin{bmatrix}a_{11}⋅b_{11}+a_{12}⋅b_{21}+a_{13}⋅b_{31} &a_{11}⋅b_{12}+a_{12}⋅b_{22}+a_{13}⋅b_{32}&a_{11}⋅b_{13}+a_{12}⋅b_{23}+a_{13}⋅b_{33} \\a_{21}⋅b_{11}+a_{22}⋅b_{21}+a_{23}⋅b_{31}&a_{21}⋅b_{12}+a_{22}⋅b_{22}+a_{23}⋅b_{32}&a_{21}⋅b_{13}+a_{22}⋅b_{23}+a_{23}⋅b_{33}\end{bmatrix} \nonumber\]
Для\(A, B\) матриці утримуються і\(C\) наступні властивості.
- Матричне множення асоціативне:\[(AB)C=A(BC).\]
- Матричне множення є розподільним:\[C(A+B)=CA+CB\]\[(A+B)C=AC+BC.\]
Зверніть увагу, що множення матриці не є комутативним.
Множення матриці\(A\) і матриці\(B\).
\[A=\begin{bmatrix}1&2\\3&4\end{bmatrix} \nonumber\]
і
\[B=\begin{bmatrix}5&6\\7&8\end{bmatrix} \nonumber\]
Рішення
Спочатку перевіряємо розміри матриць. Матриця\(A\) має розміри,\(2 × 2\) а матриця\(B\) має розміри\(2 × 2\). Внутрішні розміри однакові, тому ми можемо виконати множення. Виріб матиме розміри\(2 × 2\).
Виконуємо описані раніше операції.
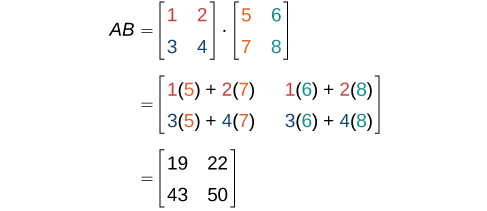
Дано\(A\) і\(B\):
- Знайти\(AB\).
- Знайти\(BA\).
\[A=\begin{bmatrix}−1&2&3\\ 4&0&5\end{bmatrix} \nonumber\]
і
\[B=\begin{bmatrix}5&−1\\-4&0\\2&3\end{bmatrix} \nonumber\]
Рішення
- Оскільки розміри\(A\) є\(2 \times 3\) та розміри\(B\) є\(3 \times 2\), ці матриці можна помножити разом, оскільки кількість стовпців у\(A\) відповідає кількості рядків у\(B\). Отриманий твір буде\(2 \times 2\) матрицею, кількість рядків в\(A\) на кількість стовпців в\(B\).
\[ \begin{align}AB&=\begin{bmatrix}−1&2&3\\4&0&5\end{bmatrix} \begin{bmatrix}5&−1\\−4&0\\2&3\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−1(5)+2(−4)+3(2)&−1(−1)+2(0)+3(3)\\4(5)+0(−4)+5(2)&4(−1)+0(0)+5(3)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−7&10\\30&11\end{bmatrix} \nonumber \end{align} \nonumber\]
- Розміри\(B\) є\(3 \times 2\) і розміри\(A\) є\(2 \times 3\). Внутрішні розміри збігаються таким чином, виріб визначено і буде\(3 \times 3\) матрицею.
\[ \begin{align}BA&=\begin{bmatrix}5&−1\\−4&0\\2&3\end{bmatrix} \begin{bmatrix} −1&2&3\\4&0&5\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}5(−1)+−1(4)&5(2)+−1(0)&5(3)+−1(5)\\−4(−1)+0(4)&−4(2)+0(0)&−4(3)+0(5)\\2(−1)+3(4)& 2(2)+3(0)&2(3)+3(5)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−9&10&10\\4&−8&−12\\10&4&21\end{bmatrix} \nonumber \end{align} \nonumber\]
Аналіз
Зверніть увагу, що\(BA\) продукти\(AB\) і не рівні.
\[AB=\begin{bmatrix}−7&10\\30&11\end{bmatrix}≠ \begin{bmatrix}−9&10&10\\4&−8&−12\\10&4&21\end{bmatrix}=BA \nonumber\]
Це ілюструє той факт, що множення матриці не є комутативним.
Так, розглянемо матрицю\(A\) з розмірністю\(3 × 4\) і матрицю\(B\) з розмірністю\(4 × 2\). Для\(AB\) виробу внутрішні розміри є\(4\) і виріб визначено, але для\(BA\) виробу внутрішні розміри є,\(2\) і\(3\) тому виріб не визначено.
Повернемося до проблеми, представленої на відкритті цього розділу. У нас є таблиця\(\PageIndex{3}\), що представляє потреби в обладнанні двох футбольних команд.
| Дикі коти | Бруд Кішки | |
|---|---|---|
| Цілі | 6 | 10 |
| Кульки | 30 | 24 |
| Трикотажні вироби | 14 | 20 |
Нам також наводяться ціни на обладнання, як показано в табл\(\PageIndex{4}\).
| Мета | $300 |
| М'яч | $10 |
| Джерсі | $30 |
Ми будемо конвертувати дані в матриці. Таким чином, матриця потреби обладнання записується як
\[E=\begin{bmatrix}6&10\\30&24\\14&20\end{bmatrix} \nonumber\]
Матриця витрат записується як
\[C=\begin{bmatrix}300&10&30\end{bmatrix} \nonumber\]
Виконуємо множення матриць для отримання витрат на обладнання.
\[ \begin{align} CE&=\begin{bmatrix}300&10&30\end{bmatrix}⋅\begin{bmatrix}6&10\\30&24\\14&20\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}300(6)+10(30)+30(14)&300(10)+10(24)+30(20)\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}2,520&3,840\end{bmatrix} \nonumber \end{align} \nonumber\]
Загальна вартість обладнання для Wildcats становить\($2,520\), а загальна вартість обладнання для грязьових кішок становить\($3,840\).
- Зберегти кожну матрицю як змінну матриці\([A], [B], [C],...\)
- Введіть операцію в калькулятор, викликаючи кожну змінну матриці за потребою.
- Якщо операція визначена, калькулятор представить матрицю розв'язку; якщо операція не визначена, програма покаже повідомлення про помилку.
Знайти\(AB−C\) дано
\(A=\begin{bmatrix}−15&25&32\\41&−7&−28\\10&34&−2\end{bmatrix}\),\(B=\begin{bmatrix}45&21&−37\\−24&52&19\\6&−48&−31\end{bmatrix}\), і\(C=\begin{bmatrix}−100&−89&−98\\25&−56&74\\−67&42&−75\end{bmatrix}\)
Рішення
На сторінці матриці калькулятора ми вводимо матрицю\(A\) вище як змінну матриці\([ A ]\), матрицю\(B\) вище як змінну матриці\([ B ]\), а матрицю\(C\) вище як змінну матриці\([ C ]\).
На головному екрані калькулятора набираємо задачу і викликаємо кожну змінну матриці за потребою.
\[[A]×[B]−[C] \nonumber\]
Калькулятор дає нам наступну матрицю.
\[\begin{bmatrix}−983&−462&136\\1,820&1,897&−856\\−311&2,032&413\end{bmatrix} \nonumber\]
Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з матрицями та матричними операціями.
Ключові поняття
- Матриця являє собою прямокутний масив чисел. Записи розташовані в рядках і стовпцях.
- Розміри матриці відносяться до кількості рядків і кількості стовпців. \(3×2\)Матриця має три рядки і два стовпці. Див\(\PageIndex{1}\). Приклад.
- Ми складаємо і віднімаємо матриці рівних розмірів шляхом додавання і віднімання відповідних записів кожної матриці. Див. Приклад\(\PageIndex{2}\)\(\PageIndex{3}\), Приклад\(\PageIndex{4}\), Приклад та Приклад\(\PageIndex{5}\).
- Скалярне множення передбачає множення кожного запису в матриці на константу. Див\(\PageIndex{6}\). Приклад.
- Перед додаванням або відніманням часто потрібно скалярне множення. Див\(\PageIndex{7}\). Приклад.
- Множення матриць можливо, коли внутрішні розміри однакові - кількість стовпців у першій матриці має збігатися з кількістю рядків у другій.
- Добуток двох матриць,\(A\) і\(B\), отримують шляхом множення кожного запису в рядку 1\(A\) на кожен запис у стовпці 1 з\(B\); потім помножити кожен запис рядка 1\(A\) на кожен запис у стовпцях 2 з\(B\), і так далі. Див. Приклад\(\PageIndex{8}\) і Приклад\(\PageIndex{9}\).
- Багато реальних проблем часто можна вирішити за допомогою матриць. Див\(\PageIndex{10}\). Приклад.
- Ми можемо використовувати калькулятор для виконання матричних операцій після збереження кожної матриці як змінної матриці. Див\(\PageIndex{11}\). Приклад.
