6.2: Експоненціальні функції
- Page ID
- 59680
- Оцініть експоненціальні функції.
- Знайти рівняння експоненціальної функції.
- Використовуйте складні процентні формули.
- Оцініть експоненціальні функції з базою\(e\).
Індія є другою за чисельністю населення країною світу з населенням близько\(1.25\) мільярда людей у 2013 році. Населення зростає зі швидкістю приблизно\(.2\%\) щороку. Якщо цей показник збережеться, чисельність населення Індії перевищить чисельність населення Китаю до 2031 року. Коли населення швидко зростає, ми часто говоримо, що зростання є «експоненціальним», тобто щось зростає дуже швидко. Для математика, однак, термін експоненціальне зростання має дуже специфічне значення. У цьому розділі ми розглянемо експоненціальні функції, які моделюють цей вид швидкого зростання.
При дослідженні лінійного зростання ми спостерігали постійну швидкість зміни — постійне число, на яке випуск збільшувався для кожної одиниці збільшення вхідних даних. Наприклад, у рівнянні нахил говорить нам\(f(x)=3x+4\), що вихід збільшується з\(3\) кожним разом, коли вхід збільшується на\(1\). Сценарій у прикладі населення Індії відрізняється, оскільки ми маємо процентну зміну за одиницю часу (а не постійна зміна) кількості людей.
Визначення експоненціальної функції
Дослідження показало, що відсоток населення, який є веганами в Сполучених Штатах, подвоївся з 2009 по 2011 рік. У 2011 році населення було веганським, дотримуючись дієти, яка не включає жодних продуктів тваринного походження — ні м'яса, птиці, риби, ні молочних продуктів, ні яєць.\(2.5\%\) Якщо цей показник збережеться, вегани\(10\%\) складуть населення США в 2015 році,\(40\%\) у 2019\(80\%\) році та 2050 році.
Що саме означає рости в геометричній прогресії? Що спільного у слова подвійний зі збільшенням відсотків? Люди хаотично кидають ці слова навколо. Чи правильно ці слова вживаються? Слова, безумовно, часто з'являються в засобах масової інформації.
- Відсоток зміни відноситься до зміни, заснованої на відсотках від початкової суми.
- Експоненціальне зростання відноситься до збільшення, засноване на постійній мультиплікативної швидкості зміни протягом рівних кроків часу, тобто процентне збільшення початкової суми з плином часу.
- Експоненціальний розпад відноситься до зменшення, засноване на постійній мультиплікативної швидкості зміни протягом рівних кроків часу, тобто процентне зменшення початкової суми з плином часу.
Щоб ми отримали чітке розуміння експоненціального зростання, давайте порівняємо експоненціальне зростання з лінійним зростанням. Побудуємо дві функції. Перша функція - експоненціальна. Ми почнемо з введення\(0\), і збільшити кожен вхід на\(1\). Ми подвоїмо відповідні послідовні виходи. Друга функція - лінійна. Ми почнемо з введення\(0\), і збільшити кожен вхід на\(1\). Додамо\(2\) до відповідних послідовних виходів (Таблиця\(\PageIndex{1}\)).
З таблиці\(\PageIndex{1}\) ми можемо зробити висновок, що для цих двох функцій експоненціальний ріст карликів лінійного зростання.
- Експоненціальне зростання відноситься до початкового значення з діапазону збільшується на той самий відсоток над рівними кроками, знайденими в області.
- Лінійне зростання відноситься до початкового значення з діапазону збільшується на ту саму величину над рівними кроками, знайденими в області.
| \(x\) | \(f(x)=2^x\) | \(g(x)=2x\) |
|---|---|---|
| \ (x\)» style="вертикальне вирівнювання: середина; "> 0 | \ (f (x) = 2^x\)» style="вертикальне вирівнювання: середина; "> 1 | \ (g (x) = 2x\)» style="вертикальне вирівнювання: середина; "> 0 |
| \ (x\)» style="вертикальне вирівнювання: середина; "> 1 | \ (f (x) = 2^x\)» style="вертикальне вирівнювання: середина; "> 2 | \ (g (x) = 2x\)» style="вертикальне вирівнювання: середина; "> 2 |
| \ (x\)» style="вертикальне вирівнювання: середина; "> 2 | \ (f (x) = 2^x\)» style="вертикальне вирівнювання: середина; "> 4 | \ (g (x) = 2x\)» style="вертикальне вирівнювання: середина; "> 4 |
| \ (x\)» style="вертикальне вирівнювання: середина; "> 3 | \ (f (x) = 2^x\)» style="вертикальне вирівнювання: середина; "> 8 | \ (g (x) = 2x\)» style="вертикальне вирівнювання: середина; "> 6 |
| \ (x\)» style="вертикальне вирівнювання: середина; "> 4 | \ (f (x) = 2^x\)» style="вертикальне вирівнювання: середина; "> 16 | \ (g (x) = 2x\)» style="вертикальне вирівнювання: середина; "> 8 |
| \ (x\)» style="вертикальне вирівнювання: середина; "> 5 | \ (f (x) = 2^x\)» style="вертикальне вирівнювання: середина; "> 32 | \ (g (x) = 2x\)» style="вертикальне вирівнювання: середина; "> 10 |
| \ (x\)» style="вертикальне вирівнювання: середина; "> 6 | \ (f (x) = 2^x\)» style="вертикальне вирівнювання: середина; "> 64 | \ (g (x) = 2x\)» style="вертикальне вирівнювання: середина; "> 12 |
Мабуть, різниця між «однаковим відсотком» і «однаковою сумою» досить істотна. Для експоненціального зростання, над рівними кроками, постійна мультиплікативна швидкість зміни призвела до подвоєння вихідних даних щоразу, коли вхід збільшувався на одиницю. Для лінійного зростання постійна адитивна швидкість зміни над рівними кроками призвела\(2\) до додавання до виходу щоразу, коли вхід був збільшений на одиницю.
Загальна форма експоненціальної функції - це\(f(x)=ab^x\), де\(a\) будь-яке ненульове число,\(b\) є додатним дійсним числом, не рівним\(1\).
- Якщо\(b>1\), функція зростає зі швидкістю, пропорційною її розміру.
- Якщо\(0<b<1\), функція розпадається зі швидкістю, пропорційною її розміру.
Давайте розглянемо функцію\(f(x)=2^x\) з нашого прикладу. Створимо таблицю (Таблицю\(\PageIndex{2}\)) для визначення відповідних виходів за інтервал в домені від\(−3\) до\(3\).
| \(x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(f(x)=2^x\) | \(2^{−3}=\dfrac{1}{8}\) | \(2^{−2}=\dfrac{1}{4}\) | \(2^{−1}=\dfrac{1}{2}\) | \(2^0=1\) | \(2^1=2\) | \(2^2=4\) | \(2^3=8\) |
Розглянемо графік,\(f\) побудувавши впорядковані пари з таблиці,\(\PageIndex{2}\) а потім зробимо кілька спостережень\(\PageIndex{1}\).
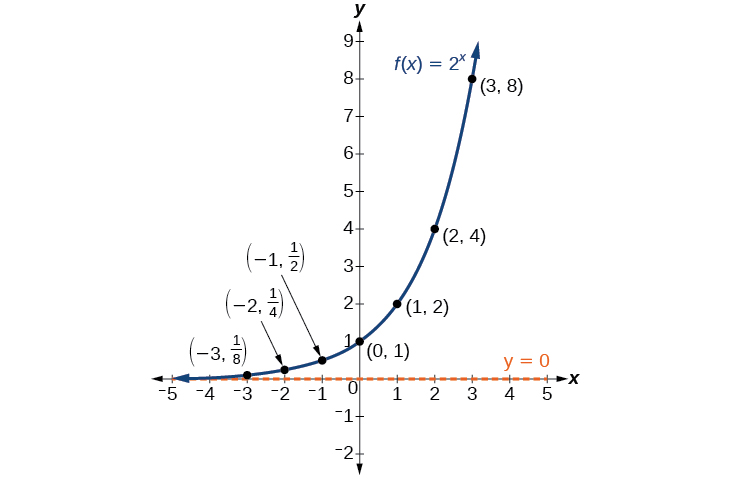
Визначимо поведінку графіка експоненціальної функції\(f(x)=2^x\) і виділимо деякі її ключові характеристики.
- домен є\((−\infty,\infty)\),
- діапазон - це\((0,\infty)\),
- як\(x\rightarrow \infty\)\(f(x)\rightarrow \infty\),
- як\(x\rightarrow −\infty\)\(f(x)\rightarrow 0\),
- \(f(x)\)постійно збільшується,
- графік ніколи не торкнеться осі x, тому що база два підняті до будь-якого показника ніколи не має результату нуля.\(f(x)\)
- \(y=0\)це горизонтальна асимптота.
- то y -перехоплення є\(1\).
Для будь-якого дійсного числа\(x\) експоненціальна функція - це функція з формою
\[f(x)=ab^x\]
де
- \(a\)є ненульовим дійсним числом, яке називається початковим значенням і
- \(b\)це будь-яке позитивне дійсне число таке, що\(b≠1\).
- Домен всіх\(f\) дійсних чисел.
- Діапазон всіх позитивних дійсних\(f\) чисел, якщо\(a>0\).
- Діапазон всіх\(f\) від'ємних дійсних чисел, якщо\(a<0\).
- Y -перехоплення є\((0,a)\), а горизонтальна асимптота є\(y=0\).
Які з наведених нижче рівнянь не є експоненціальними функціями?
- \(f(x)=4^{3(x−2)}\)
- \(g(x)=x^3\)
- \(h(x)=\left(\dfrac{1}{3}\right)^x\)
- \(j(x)=(−2)^x\)
Рішення
За визначенням експоненціальна функція має константу як базу і незалежну змінну як показник. Таким чином,\(g(x)=x^3\) не представляє експоненціальну функцію, оскільки база є незалежною змінною. По суті,\(g(x)=x^3\) це силова функція.
Нагадаємо, що основою\(b\) експоненціальної функції завжди є позитивна константа, і\(b≠1\). Таким чином,\(j(x)={(−2)}^x\) не представляє експоненціальну функцію, оскільки база,\(−2\), менше, ніж\(0\).
Які з наступних рівнянь представляють експоненціальні функції?
- \(f(x)=2x^2−3x+1\)
- \(g(x)={0.875}^x\)
- \(h(x)=1.75x+2\)
- \(j(x)={1095.6}^{−2x}\)
- Відповідь
-
\(g(x)={0.875}^x\)і\(j(x)={1095.6}^{−2x}\) представляють експоненціальні функції.
Оцінка експоненціальних функцій
Нагадаємо, що основою експоненціальної функції має бути додатне дійсне число, відмінне від\(1\) .Чому ми обмежуємо базу bb додатними значеннями? Переконатися в тому, що на виходах будуть дійсні числа. Поспостерігайте, що відбувається, якщо база не позитивна:
- Нехай\(b=−9\) і\(x=\dfrac{1}{2}\). Тоді\(f(x)=f\left(\dfrac{1}{2}\right)={(−9)}^{\dfrac{1}{2}}=\sqrt{−9}\), що не є дійсним числом.
Чому ми обмежуємо базу позитивними значеннями, крім\(1\)? Тому що база\(1\) призводить до постійної функції. Поспостерігайте, що відбувається, якщо основа\(1\):
- Нехай\(b=1\). Тоді\(f(x)=1^x=1\) за будь-яке значення\(x\).
Для оцінки експоненціальної функції з формою\(f(x)=b^x\) просто\(x\) підставляємо задане значення, і обчислюємо отриману потужність. Наприклад:
Нехай\(f(x)=2^x\). Що таке\(f(3)\)?
\[\begin{align*} f(x)&= 2^x\\ f(3)&= 2^3 \qquad \text{Substitute } x=3\\ &= 8 \qquad \text{Evaluate the power} \end{align*}\]
Для оцінки експоненціальної функції з формою, відмінною від основної форми, важливо дотримуватися порядку операцій. Наприклад:
Нехай\(f(x)=30{(2)}^x\). Що таке\(f(3)\)?
\[\begin{align*} f(x)&= 30{(2)}^x\\ f(3)&= 30{(2)}^3 \qquad \text{Substitute } x=3\\ &= 30(8) \qquad \text{Simplify the power first}\\ &= 240 \qquad \text{Multiply} \end{align*}\]
Зверніть увагу, що якби порядок операцій не дотримувався, результат був би невірним:
\[f(3)=30{(2)}^3≠{60}^3=216,000 \nonumber\]
Нехай\(f(x)=5{(3)}^{x+1}\). Оцінюйте\(f(2)\) без використання калькулятора.
Рішення
Слідкуйте за порядком операцій. Обов'язково зверніть увагу на дужки.
\[\begin{align*} f(x)&= 5{(3)}^{x+1}\\ f(2)&= 5{(3)}^{2+1} \qquad \text{Substitute } x=2\\ &= 5{(3)}^3 \qquad \text{Add the exponents}\\ &= 5(27) \qquad \text{Simplify the power}\\ &= 135 \qquad \text{Multiply} \end{align*}\]
Нехай\(f(x)=8{(1.2)}^{x−5}\). Оцініть\(f(3)\) за допомогою калькулятора. Округлення до чотирьох знаків після коми.
- Відповідь
-
\(5.5556\)
Визначення експоненціального зростання
Оскільки вихід експоненціальних функцій зростає дуже швидко, термін «експоненціальне зростання» часто використовується в повсякденній мові для опису всього, що швидко зростає або зростає. Однак експоненціальне зростання можна визначити точніше в математичному сенсі. Якщо швидкість зростання пропорційна присутній сумі, функція моделює експоненціальне зростання.
Функція, яка моделює експоненціальне зростання, зростає на швидкість, пропорційну присутній сумі. Для будь-якого дійсного числа\(x\) і будь-яких позитивних дійсних чисел\(a\) і\(b\) таких\(b≠1\), що експоненціальна функція зростання має вигляд
\[f(x)=ab^x\]
де
- \(a\)початкове або початкове значення функції.
- \(b\)це фактор росту або множник зростання на одиницю\(x\).
У більш загальних рисах ми маємо експоненціальну функцію, в якій постійна база піднімається до змінної експоненти. Щоб розмежувати лінійні та експоненціальні функції, розглянемо дві компанії, А і Б. Компанія А має\(100\) магазини і розширюється, відкриваючи\(50\) нові магазини на рік, тому її зростання може бути представлено функцією\(A(x)=100+50x\). Компанія Б має\(100\) магазини і розширюється за рахунок збільшення кількості магазинів з\(50\%\) кожним роком, тому її зростання може бути представлений функцією\(B(x)=100{(1+0.5)}^x\).
Кілька років зростання цих компаній проілюстровані в табл\(\PageIndex{3}\).
| Рік,\(x\) | Магазини, Компанія A | Магазини, Компанія B |
|---|---|---|
| \ (x\) ">\(0\) | \(100+50(0)=100\) | \(100{(1+0.5)}^0=100\) |
| \ (x\) ">\(1\) | \(100+50(1)=150\) | \(100{(1+0.5)}^1=150\) |
| \ (x\) ">\(2\) | \(100+50(2)=200\) | \(100{(1+0.5)}^2=225\) |
| \ (x\) ">\(3\) | \(100+50(3)=250\) | \(100{(1+0.5)}^3=337.5\) |
| \ (x\) ">\(x\) | \(A(x)=100+50x\) | \(B(x)=100{(1+0.5)}^x\) |
Графіки порівняння кількості магазинів для кожної компанії за п'ятирічний період наведені на малюнку\(\PageIndex{2}\). Ми бачимо, що при експоненціальному зростанні кількість магазинів збільшується набагато швидше, ніж при лінійному зростанні.
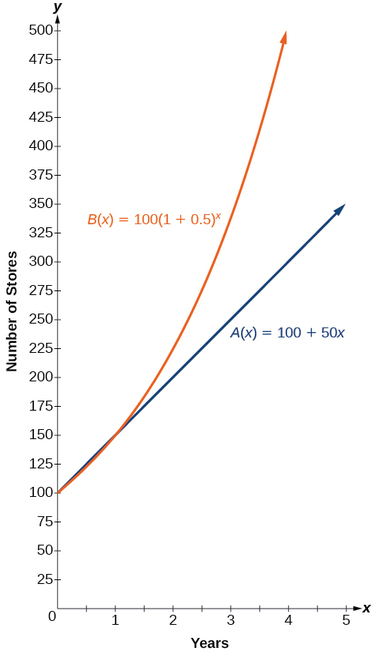
Зверніть увагу, що домен для обох функцій є\([0,\infty)\), і діапазон для обох функцій є\([100,\infty)\). Після першого року компанія B завжди має більше магазинів, ніж компанія A.
Тепер звернемо увагу на функцію, що представляє кількість магазинів для компанії\(B\),\(B(x)=100{(1+0.5)}^x\). У цій експоненціальній функції,\(100\) представляє початкову кількість магазинів,\(0.50\) представляє швидкість зростання і\(1+0.5=1.5\) являє собою фактор зростання. Узагальнюючи далі, ми можемо записати цю функцію як\(B(x)=100{(1.5)}^x\), де\(100\) початкове значення,\(1.5\) називається \(x\)базовим, і називається показником.
На початку цього розділу ми дізналися, що населення Індії становило близько\(1.25\) мільярда в 2013 році, при щорічному темпі зростання близько\(1.2\%\). Така ситуація представлена функцією зростання\(P(t)=1.25{(1.012)}^t\), де\(t\) знаходиться кількість років з 2013 року. До найближчої тисячної, яким буде населення Індії в 2031 році?
Рішення
Щоб оцінити чисельність населення в 2031 році, ми оцінюємо моделі для\(t=18\), тому що 2031\(18\) рік - це роки після 2013 року. Округлення до найближчої тисячної,
\[P(18)=1.25{(1.012)}^{18}≈1.549 \nonumber\]
У 2031 році в Індії буде близько\(1.549\) мільярда людей.
Населення Китаю становило близько\(1.39\) мільярда в 2013 році, при щорічному темпі зростання близько\(0.6\%\). Така ситуація представлена функцією зростання\(P(t)=1.39{(1.006)}^t\), де\(t\) число років з 2013 року.До найближчої тисячної, яким буде населення Китаю на 2031 рік? Як це порівнюється з прогнозом населення, який ми зробили для Індії на прикладі\(\PageIndex{3}\)?
- Відповідь
-
Близько\(1.548\) мільярда людей; до 2031 року населення Індії перевищить чисельність населення Китаю приблизно на\(0.001\) мільярд, або\(1\) мільйон людей.
Пошук рівнянь експоненціальних функцій
У попередніх прикладах нам дали експоненціальну функцію, яку ми потім оцінювали для заданого вводу. Іноді нам дають інформацію про експоненціальну функцію, не знаючи функції явно. Ми повинні використовувати інформацію, щоб спочатку написати форму функції, потім визначити константи\(a, a\) і\(b, b\), і оцінити функцію.
- Якщо одна з точок даних має вигляд\((0,a)\), то\(a\) це початкове значення. Використовуючи\(a\), підставляємо другу точку в рівняння\(f(x)=a{(b)}^x\), і вирішуємо для\(b\).
- Якщо жодна з точок даних не має вигляду\((0,a)\), підставляйте обидві точки на два рівняння з формою\(f(x)=a{(b)}^x\). Вирішити отриману систему двох рівнянь в двох невідомих\(a\) і знайти\(b\).
- Використовуючи\(a\) і,\(b\) знайдене в кроках вище, запишіть експоненціальну функцію у вигляді\(f(x)=a{(b)}^x\).
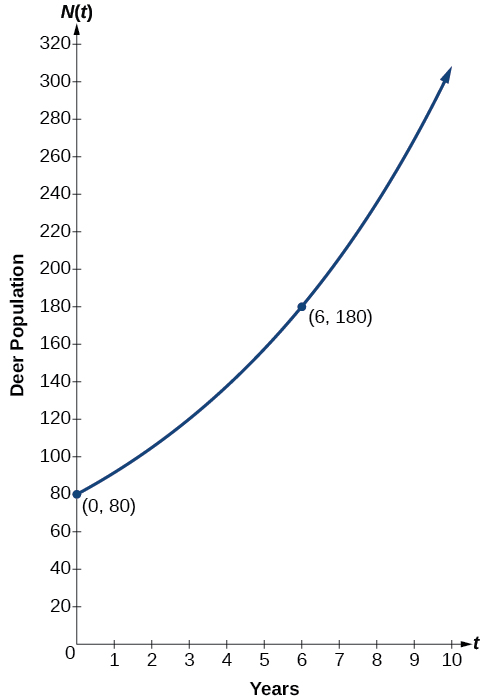
У 2006 році\(80\) олені були введені в притулок для дикої природи. До 2012 року популяція виросла до\(180\) оленів. Населення зростало в геометричній прогресії. Напишіть алгебраїчну функцію,\(N(t)\) що представляє популяції\((N)\) оленів з плином часу\(t\).
Рішення
Ми дозволяємо нашій незалежній змінній\(t\) бути кількістю років після 2006 року. Таким чином, інформація, наведена в задачі, може бути записана у вигляді пар введення-виведення: (0, 80) і (6, 180). Зверніть увагу, що, вибравши нашу вхідну змінну, яка буде вимірюватися як роки після 2006, ми дали собі початкове значення для функції,\(a=80\). Тепер ми можемо підставити другу точку в рівняння,\(N(t)=80b^t\) щоб знайти\(b\):
\[\begin{align*} N(t)&= 80b^t\\ 180&= 80b^6 \qquad \text{Substitute using point } (6, 180)\\ \dfrac{9}{4}&= b^6 \qquad \text{Divide and write in lowest terms}\\ b&= {\left (\dfrac{9}{4} \right )}^{\tfrac{1}{6}} \qquad \text{Isolate b using properties of exponents}\\ b&\approx 1.1447 \qquad \text{Round to 4 decimal places} \end{align*}\]
Якщо не вказано інше, не округляйте будь-які проміжні розрахунки. Потім округляємо остаточну відповідь на чотири місця для залишку цього розділу.
Експоненціальна модель для популяції оленів є\(N(t)=80{(1.1447)}^t\). (Зауважте, що ця експоненціальна функція моделює короткочасне зростання. Оскільки входи стають великими, вихід буде ставати все більшим, настільки, що модель може бути не корисною в довгостроковій перспективі.)
Ми можемо графікувати нашу модель, щоб спостерігати за зростанням популяції оленів у притулку з плином часу. Зверніть увагу, що графік на малюнку\(\PageIndex{3}\) проходить через початкові точки, наведені в задачі,\((0, 80)\) і\((6, 180)\). Ми також можемо бачити, що домен для функції є\([0,\infty)\), а діапазон для функції є\([80,\infty)\).
Популяція вовків зростає в геометричній прогресії. У 2011 році\(129\) вовки були підраховані. До 2013 року популяція досягла\(236\) вовків. Які дві точки можна використовувати для отримання експоненціального рівняння, що моделює цю ситуацію? Напишіть рівняння, що представляє\(N\) популяції вовків з плином часу\(t\).
- Відповідь
-
\((0,129)\)і\((2,236)\);\(N(t)=129{(1.3526)}^t\)
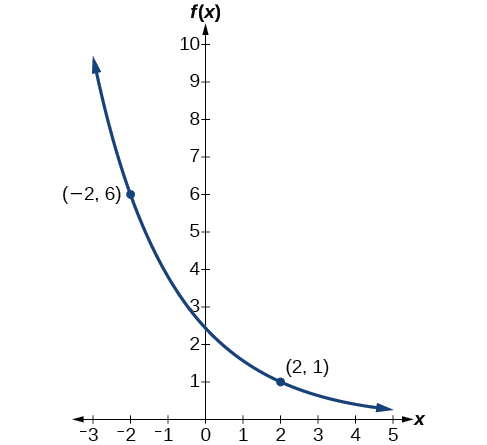
Знайдіть експоненціальну функцію, яка проходить через точки\((−2,6)\) і\((2,1)\).
Рішення
Оскільки у нас немає початкового значення, ми підставляємо обидві точки в рівняння форми\(f(x)=ab^x\), а потім вирішуємо систему для\(a\) і\(b\).
- Заміна\((−2,6)\) дає\(6=ab^{−2}\)
- Заміна\((2,1)\) дає\(1=ab^2\)
Використовуйте перше рівняння для вирішення\(a\) за термінами\(b\):
\[\begin{align*} 6&= ab^{-2}\\ \dfrac{6}{b^{-2}}&= a \qquad \text{Divide}\\ a&= 6b^2 \qquad \text{Use properties of exponents to rewrite the denominator} \end{align*}\]
Підставляємо a у другому рівнянні і вирішуємо для\(b\):
\[\begin{align*} 1&= ab^{2}\\ 1&= 6b^2 b^2\\ &= 6b^4 \qquad \text{Substitute a}\\ b&= \left (\dfrac{1}{6} \right )^{\tfrac{1}{4}} \qquad \text{Round 4 decimal places rewrite the denominator}\\ b&\approx 0.6389 \end{align*}\]
Використовуйте значення\(b\) в першому рівнянні для вирішення значення\(a\):
\[\begin{align*} a&= 6b^{2}\\ &\approx 6(0.6389)^2 \\ &\approx 2.4492 \end{align*}\]
Таким чином, рівняння є\(f(x)=2.4492{(0.6389)}^x\).
Ми можемо графікувати нашу модель, щоб перевірити нашу роботу. Зверніть увагу, що графік на малюнку\(\PageIndex{4}\) проходить через початкові точки, наведені в задачі,\((−2, 6)\) і\((2, 1)\). Графік є прикладом експоненціальної функції розпаду.
З огляду на дві точки\((1,3)\) і\((2,4.5)\), знайдіть рівняння експоненціальної функції, яка проходить через ці дві точки.
- Відповідь
-
\(f(x)=2{(1.5)}^x\)
Так, за умови, що дві точки знаходяться або над віссю x, або обидві нижче осі x і мають різні координати x. Але майте на увазі, що ми також повинні знати, що графік є, по суті, експоненціальна функція. Не кожен графік, який виглядає експоненціальним, насправді є експоненціальним. Нам потрібно знати, що графік базується на моделі, яка показує однаковий відсоток зростання з кожним збільшенням одиниці\(x\), що в багатьох випадках реального світу передбачає час.
- Спочатку виділіть дві точки на графіку. Виберіть\(y\) -intercept як одну з двох точок, коли це можливо. Намагайтеся вибирати точки, які знаходяться якомога далі один від одного, щоб зменшити похибку округлення.
- Якщо однією з точок даних є\(y\) -intercept\((0,a)\), то\(a\) є початковим значенням. Використовуючи\(a\), підставляємо другу точку в\(f(x)=a{(b)}^x\) рівняння і вирішуємо для\(b\)
- Якщо жодна з точок даних не має вигляду\((0,a)\), підставляйте обидві точки на два рівняння з формою\(f(x)=a{(b)}^x\). Вирішити отриману систему двох рівнянь в двох невідомих\(a\) і знайти\(b\).
- Запишіть експоненціальну функцію,\(f(x)=a{(b)}^x\).
Знайдіть рівняння для експоненціальної функції, зображеної на рисунку\(\PageIndex{5}\).
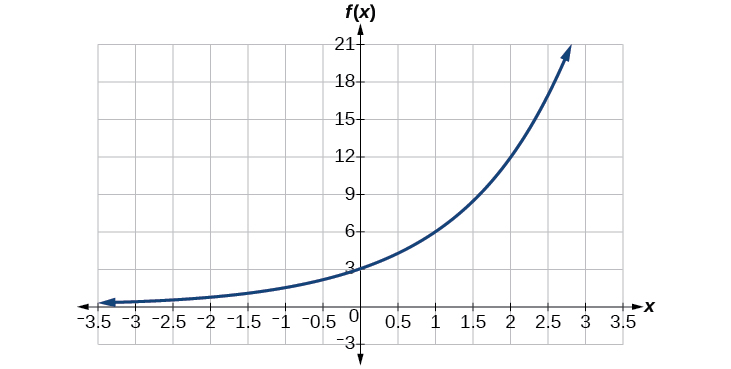
Рішення
Ми можемо вибрати \(y\)-перехоплення графіка\((0,3)\), як наш перший пункт. Це дає нам початкове значення,\(a=3\). Далі виберіть точку на кривій на деякій відстані від якої\((0,3)\) є цілочисельні координати. Одним з таких моментом є\((2,12)\).
\[\begin{align*} y&= ab^x \qquad \text{Write the general form of an exponential equation}\\ y&= 3b^x \qquad \text{Substitute the initial value } 3 \text{ for } a\\ 12&= 3b^2 \qquad \text{Substitute in 12 for } y \text{ and } 2 \text{ for } x\\ 4&= b^2 \qquad \text{Divide by }3\\ b&= \pm 2 \qquad \text{Take the square root} \end{align*}\]
Тому що ми обмежуємося позитивними значеннями\(b\), ми будемо використовувати\(b=2\). \(b\)Підставляємо\(a\) і в стандартну форму, щоб отримати рівняння\(f(x)=3{(2)}^x\).
Знайдіть рівняння для експоненціальної функції, зображеної на рисунку\(\PageIndex{6}\).
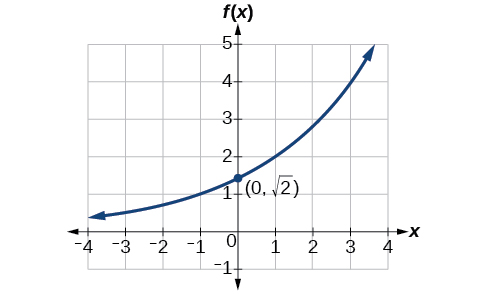
- Відповідь
-
\(f(x)=\sqrt{2}{(\sqrt{2})}^x\). Відповіді можуть відрізнятися через помилку округлення. Відповідь повинен бути дуже близький до\(1.4142{(1.4142)}^x\).
- Натисніть [СТАТ].
- Очистити всі існуючі записи в стовпцях L1 або L2.
- У L1 введіть задані координати x.
- У L2 введіть відповідні y -координати.
- Знову натисніть [STAT]. Курсор праворуч до CALC, прокрутіть униз до ExpReg (експоненціальна регресія) і натисніть [ENTER].
- На екрані відображаються значення a і b в експоненціальному рівнянні\(y=a⋅b^x\).
Використовуйте графічний калькулятор, щоб знайти експоненціальне рівняння, яке включає точки\((2,24.8)\) і\((5,198.4)\).
Рішення
Дотримуйтесь наведених вище вказівок. Спочатку натисніть [STAT], [EDIT], [1: Редагувати...] і очистіть списки L1 і L2. Далі в стовпці L1 введіть\(x\) -координати,\(2\) і\(5\). Зробіть те ж саме в стовпці L2 для\(y\) -координат,\(24.8\) і\(198.4\).
Тепер натисніть [STAT], [CALC], [0: ExpReg] і натисніть [ENTER]. Значення\(a=6.2\) і\(b=2\) будуть відображатися. Експоненціальне рівняння є\(y=6.2⋅2^x\).
Використовуйте графічний калькулятор, щоб знайти експоненціальне рівняння, яке включає точки\((3, 75.98)\) і\((6, 481.07)\).
- Відповідь
-
\(y≈12⋅{1.85}^x\)
Застосування формули складного відсотка
Ощадні інструменти, в які постійно реінвестуються доходи, такі як пайові фонди та пенсійні рахунки, використовують складні відсотки. Під терміном складання розуміються відсотки, зароблені не тільки на первісну вартість, але і на накопичену вартість рахунку.
Річна процентна ставка (APR) рахунку, яку також називають номінальною ставкою, - це річна процентна ставка, зароблена інвестиційним рахунком. Термін номінальний використовується, коли компаундування відбувається кілька разів, крім одного разу на рік. Насправді, коли відсотки посилюються більше одного разу на рік, ефективна процентна ставка в кінцевому підсумку перевищує номінальну ставку! Це потужний інструмент для інвестування.
Ми можемо обчислити складні відсотки, використовуючи формулу складних відсотків, яка є експоненціальною функцією змінних часу\(t\)\(P\)\(APR\)\(r\), основної суми та кількості періодів складення в році\(n\):
\[A(t)=P{\left (1+\dfrac{r}{n} \right )}^{nt} \nonumber\]
Наприклад, дотримуйтесь таблицю\(\PageIndex{4}\), в якій показаний результат інвестування\($1,000\) при\(10\%\) протягом одного року. Зверніть увагу, як значення рахунку збільшується з збільшенням частоти складання.
| Частота | Значення за\(1\) роком |
|---|---|
| Щорічно | \ (1\) рік">\($1100\) |
| Піврічно | \ (1\) рік">\($1102.50\) |
| Квартально | \ (1\) рік">\($1103.81\) |
| Щомісячно | \ (1\) рік">\($1104.71\) |
| Щодня | \ (1\) рік">\($1105.16\) |
Складні відсотки можна розрахувати за формулою
\[A(t)=P{\left (1+\dfrac{r}{n} \right )}^{nt}\]
де
- \(A(t)\)це вартість рахунку,
- \(t\)вимірюється роками,
- \(P\)початкова сума рахунку, яку часто називають основною, або більш загальною поточною вартістю,
- \(r\)річна процентна ставка (APR), виражена у вигляді десяткового числа, і
- \(n\)кількість періодів компаундирования в одному році.
Якщо ми інвестуємо\($3,000\) в інвестиційний рахунок, сплачуючи\(3\%\) відсотки щоквартально, скільки коштуватиме рахунок у\(10\) роках?
Рішення
Тому що ми починаємо з\($3,000\),\(P=3000\). Наша процентна ставка є\(3\%\), так\(r = 0.03\). Оскільки ми складаємо щоквартально, ми складаємо\(4\) рази на рік, так що\(n=4\). Ми хочемо знати вартість рахунку в\(10\) роках, тому шукаємо\(A(10)\), значення коли\(t = 10\).
\[\begin{align*} A(t)&= P{\left (1+\dfrac{r}{n} \right )}^{nt} \qquad \text{Use the compound interest formula}\\ A(10)&= 3000{\left (1+\dfrac{0.03}{4} \right )}^{(4)\cdot (10)} \qquad \text{Substitute using given values}\\ &\approx \$4045.05 \qquad \text{Round to two decimal places} \end{align*}\]
Рахунок буде коштувати приблизно\($4,045.05\) через\(10\) роки.
Початкові інвестиції\($100,000\) під\(12\%\) відсотки посилюються щотижня (використання\(52\) тижнів у році). Чого коштуватиме інвестиція через\(30\) роки?
- Відповідь
-
про\($3,644,675.88\)
План 529 - це план заощаджень коледжу, який дозволяє родичам вкладати гроші для оплати майбутнього навчання дитини в коледжі; рахунок зростає без оподаткування. Лілі хоче створити обліковий запис 529 для своєї нової внучки і хоче, щоб рахунок зростав\($40,000\) протягом\(18\) багатьох років. Вона вважає, що рахунок буде заробляти в\(6\%\) сукупності півроку (два рази на рік). До найближчого долара, скільки Лілі потрібно буде інвестувати на рахунок зараз?
Рішення
Номінальна процентна ставка становить\(6\%\), так\(r=0.06\). Відсотки посилюються двічі на рік, так що\(k=2\).
Ми хочемо знайти початкові інвестиції\(P\), необхідні для того, щоб вартість рахунку коштувала\($40,000\) через\(18\) роки. Підставте задані значення в формулу складних відсотків, і вирішіть для\(P\).
\[\begin{align*} A(t)&= P{\left (1+\dfrac{r}{n} \right )}^{nt} \qquad \text{Use the compound interest formula}\\ 40,000&= P{\left (1+\dfrac{0.06}{2} \right )}^{2(18)} \qquad \text{Substitute using given values } A, r, n, t\\ 40,000&= P{(1.03)}^{36} \qquad \text{Simplify}\\ \dfrac{40,000}{ {(1.03)}^{36} }&= P \qquad \text{Isolate } P\\ P&\approx \$13,801 \qquad \text{Divide and round to the nearest dollar} \end{align*}\]
Лілії потрібно буде інвестувати\($13,801\), щоб мати\($40,000\) в\(18\) роки.
Зверніться до Приклад\(\PageIndex{9}\). До найближчого долара, скільки потрібно було б інвестувати Лілі, якщо рахунок збільшується щоквартально?
- Відповідь
-
\($13,693\)
Оцінка функцій з базою\(e\)
Як ми бачили раніше, сума, зароблена на рахунку, збільшується зі збільшенням частоти складання. Таблиця\(\PageIndex{5}\) показує, що збільшення від річного до піврічного складання більше, ніж збільшення від місячного до щоденного складання. Це може призвести до того, що ми запитаємо, чи продовжиться ця закономірність.
Вивчіть вартість\($1\) вкладеної під\(100\%\) відсотки за\(1\) рік, складену на різних частотах, перерахованих в табл\(\PageIndex{5}\).
| Частота | \(A(t)={\left (1+\dfrac{1}{n} \right )}^n\) | Значення |
|---|---|---|
| Щорічно | \ (A (t) = {\ ліворуч (1+\ dfrac {1} {n}\ праворуч)} ^n\)» style="вертикальне вирівнювання: середина; ">\({\left (1+\dfrac{1}{1} \right )}^1\) | \($2\) |
| Піврічно | \ (A (t) = {\ ліворуч (1+\ dfrac {1} {n}\ праворуч)} ^n\)» style="вертикальне вирівнювання: середина; ">\({\left (1+\dfrac{1}{2} \right )}^2\) | \($2.25\) |
| Квартально | \ (A (t) = {\ ліворуч (1+\ dfrac {1} {n}\ праворуч)} ^n\)» style="вертикальне вирівнювання: середина; ">\({\left (1+\dfrac{1}{4} \right )}^4\) | \($2.441406\) |
| Щомісячно | \ (A (t) = {\ ліворуч (1+\ dfrac {1} {n}\ праворуч)} ^n\)» style="вертикальне вирівнювання: середина; ">\({\left (1+\dfrac{1}{12} \right )}^{12}\) | \($2.613035\) |
| Щодня | \ (A (t) = {\ ліворуч (1+\ dfrac {1} {n}\ праворуч)} ^n\)» style="вертикальне вирівнювання: середина; ">\({\left (1+\dfrac{1}{365} \right )}^{365}\) | \($2.714567\) |
| Погодинно | \ (A (t) = {\ ліворуч (1+\ dfrac {1} {n}\ праворуч)} ^n\)» style="вертикальне вирівнювання: середина; ">\({\left (1+\dfrac{1}{8760} \right )}^{8760}\) | \($2.718127\) |
| Раз на хвилину | \ (A (t) = {\ ліворуч (1+\ dfrac {1} {n}\ праворуч)} ^n\)» style="вертикальне вирівнювання: середина; ">\({\left (1+\dfrac{1}{525600} \right )}^{525600}\) | \($2.718279\) |
| Раз в секунду | \ (A (t) = {\ ліворуч (1+\ dfrac {1} {n}\ праворуч)} ^n\)» style="вертикальне вирівнювання: середина; ">\({\left (1+\dfrac{1}{31536000} \right )}^{31536000}\) | \($2.718282\) |
Ці значення, здається, наближаються до межі, оскільки\(n\) збільшуються без обмежень. Насправді, коли\(n\) стає все більшим і більшим, вираз\({\left (1+\dfrac{1}{n} \right )}^n\) наближається до числа, яке так часто використовується в математиці, що має власну назву: буква\(e\). Це значення є ірраціональним числом, а це означає, що його десяткове розширення триває вічно, не повторюючись. Його наближення до шести знаків після коми показано нижче.
Буква\(e\) являє собою ірраціональне число
\[{\left (1+\dfrac{1}{n} \right )}^n\]
як\(n\) збільшується без прив'язки
Лист\(e\) використовується як основа для багатьох реальних експоненціальних моделей. Для роботи з\(e\) базою використовуємо наближення,\(e≈2.718282\). Константа була названа швейцарським математиком Леонардом Ейлером (1707—1783), який вперше дослідив і відкрив багато її властивостей.
Розрахувати\(e^{3.14}\). Округлення до п'яти знаків після коми.
Рішення
На калькуляторі натисніть кнопку з написом\([e^x]\). У вікні відображається\([e {}^( ]\). Введіть,\(3.14\) а потім закрийте дужки,\([)]\). Натисніть [ENTER]. Округлення до\(5\) десяткових знаків,\(e^{3.14}≈23.10387\). Увага: Багато наукових калькуляторів мають кнопку «Exp», яка використовується для введення чисел в наукові позначення. Він не використовується для пошуку повноважень\(e\).
Скористайтеся калькулятором, щоб знайти\(e^{−0.5}\). Округлення до п'яти знаків після коми.
- Відповідь
-
\(e^{−0.5}≈0.60653\)
Дослідження безперервного зростання
Поки що ми працювали з раціональними основами для експоненціальних функцій. Для більшості реальних явищ, однак,\(e\) використовується як основа для експоненціальних функцій. Експоненціальні моделі, які використовують\(e\) як основу, називаються моделями безперервного зростання або розпаду. Ми бачимо ці моделі у фінансах, інформатиці та більшості наук, таких як фізика, токсикологія та динаміка рідини.
Для всіх дійсних чисел\(t\), а також всіх позитивних чисел\(a\) і\(r\), безперервне зростання або занепад представлений формулою
\[A(t)=ae^{rt}\]
де
- \(a\)є початковим значенням,
- \(r\)це безперервний темп зростання в одиницю часу,
- \(t\)це минулий час.
Якщо\(r>0\), то формула являє собою безперервне зростання. Якщо\(r<0\), то формула являє собою безперервний розпад.
Для бізнес-додатків формула безперервного зростання називається формулою безперервного компаундування і приймає форму
\[A(t)=Pe^{rt}\]
де
- \(P\)є основним або початковим інвестованим,
- \(r\)зростання або процентна ставка за одиницю часу,
- \(t\)термін або термін інвестування.
- Використовуйте інформацію в задачі, щоб визначити\(a\), початкове значення функції.
- Використовуйте інформацію в задачі для визначення темпів зростання\(r\).
- Якщо проблема стосується безперервного зростання, то\(r>0\).
- Якщо проблема відноситься до безперервного гниття, то\(r<0\).
- Використовуйте інформацію в проблемі, щоб визначити час\(t\).
- Підставте задану інформацію в формулу безперервного зростання і вирішіть для\(A(t)\).
Людина, вкладена\($1,000\) в рахунок заробляє номінал\(10\%\) в рік, постійно посилюється. Скільки було на рахунку в кінці одного року?
Рішення
Оскільки рахунок зростає в ціні, це постійна проблема ускладнення зі швидкістю зростання\(r=0.10\). Початкові інвестиції були\($1,000\), так\(P=1000\). Використовуємо формулу безперервного компаундування, щоб знайти значення за\(t=1\) роком:
\[\begin{align*} A(t)&= Pe^{rt} \qquad \text{Use the continuous compounding formula}\\ &= 1000{(e)}^{0.1} \qquad \text{Substitute known values for } P, r, t\\ &\approx 1105.17 \qquad \text{Use a calculator to approximate} \end{align*}\]
Рахунок коштує\($1,105.17\) через рік.
Людина інвестує\($100,000\) під номінальний\(12\%\) відсоток в рік, що посилюється безперервно. Якою буде вартість інвестицій в\(30\) роках?
- Відповідь
-
\($3,659,823.44\)
\(Radon-222\)розпадається з безперервною швидкістю\(17.3\%\) на добу. Скільки буде\(100 mg\)\(Radon-222\) гниття в\(3\) днях?
Рішення
Так як речовина гниє, швидкість,,\(17.3\%\), негативна. Отже,\(r = −0.173\). Початкова кількість\(Radon-222\) склала\(100\) мг, так\(a=100\). Використовуємо формулу безперервного розпаду, щоб знайти значення через\(t=3\) дні:
\[\begin{align*} A(t)&= ae^{rt} \qquad \text{Use the continuous growth formula}\\ &= 100e6{-0.173(3)} \qquad \text{Substitute known values for } a, r, t\\ &\approx 59.5115 \qquad \text{Use a calculator to approximate} \end{align*}\]
Так\(59.5115\) мг\(Radon-222\) залишиться.
Використовуючи дані в прикладі\(\PageIndex{12}\), скільки\(Radon-222\) залишиться через рік?
- Відповідь
-
\(3.77E-26\)(Це калькулятор позначення для числа, записаного як\(3.77×10^{−26}\) у науковому позначенні. Хоча вихід експоненціальної функції ніколи не дорівнює нулю, це число настільки близьке до нуля, що для всіх практичних цілей ми можемо прийняти нуль як відповідь.)
Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з експоненціальними функціями.
- Функція експоненціального зростання
- Складні відсотки
Ключові рівняння
| визначення експоненціальної функції | \(f(x)=b^x\), де\(b>0\),\(b≠1\) |
| визначення експоненціального зростання | \(f(x)=ab^x\), де\(a>0\)\(b>0\),\(b≠1\) |
| формула складного відсотка |
\(A(t)=P{(1+\dfrac{r}{n})}^{nt}\), де\(A(t)\) - вартість рахунку в момент\(t\) \(t\)це кількість років \(P\)це початкова інвестиція, яку часто називають основною \(r\)річна процентна ставка (APR), або номінальна ставка \(n\)кількість періодів компаундирования в одному році |
| формула безперервного зростання | \(A(t)=ae^{rt}\), Де\(t\) число одиниць часових періодів зростання\(a\) - це початкова сума (у формулі безперервного складання a замінюється на\(P\), основна)\(e\) - математична константа,\(e≈2.718282\) |
Ключові концепції
- Експоненціальна функція визначається як функція з додатною константою, відмінною від\(1\) зведеної до змінної експоненти. Див. Приклад.
- Функція оцінюється шляхом розв'язання за певним значенням. Див. Приклад і Приклад.
- Експоненціальну модель можна знайти, коли відомі темпи зростання і початкове значення. Див. Приклад.
- Експоненціальну модель можна знайти, коли відомі дві точки даних з моделі. Див. Приклад.
- Експоненціальну модель можна знайти за допомогою двох точок даних з графіка моделі. Див. Приклад.
- Експоненціальну модель можна знайти за допомогою двох точок даних з графіка та калькулятора. Див. Приклад.
- Вартість рахунку в будь-який час\(t\) може бути розрахована за формулою складних відсотків, коли відомі основні, річні процентні ставки та періоди складання. Див. Приклад.
- Початкові інвестиції рахунку можна знайти за допомогою формули складних відсотків, коли відомі значення рахунку, річна процентна ставка, періоди складання та тривалість життя рахунку. Див. Приклад.
- Число\(e\) - математична константа, яка часто використовується як основа моделей експоненціального зростання та розпаду реального світу. Його десяткове наближення є\(e≈2.718282\).
- Наукові та графічні калькулятори мають ключ\([ex]\) або\([exp(x)]\) для розрахунку потужностей\(e\). Див. Приклад.
- Моделі безперервного зростання або розпаду - це експоненціальні моделі, які використовують\(e\) як основу. Моделі безперервного росту та розпаду можна знайти, коли відомі початкове значення та швидкість зростання або розпаду. Див. Приклад і Приклад.
