Skip to main content
LibreTexts - Ukrayinska

6.4: Логарифмічні функції

  1. Last updated
  2. Save as PDF
  • Page ID
    59645

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання
    • Перетворення з логарифмічного в експоненціальну форму.
    • Перетворення з експоненціальної в логарифмічну форму.
    • Оцініть логарифми.
    • Використовуйте загальні логарифми.
    • Використовуйте натуральні логарифми.

    У 2010 році на Гаїті стався сильний землетрус, зруйнувавши або пошкодивши понад 285,000 будинків. Через рік інший, сильніший землетрус спустошив Хонсю, Японія, знищивши або пошкодивши понад 332 000 будівель, як показано на малюнку\(\PageIndex{1}\). Незважаючи на те, що обидва завдали значної шкоди, землетрус 2011 року був у 100 разів сильнішим, ніж землетрус на Гаїті. Звідки ми знаємо? Величини землетрусів вимірюються за шкалою, відомою як шкала Ріхтера. Гаїтянський землетрус зареєстрував 7,0 за шкалою Ріхтера, тоді як японський землетрус зареєстрував 9,0.

    Фото наслідків землетрусу в Японії з акцентом на японський прапор.

    Ілюстрація\(\PageIndex{1}\): Спустошення 11 березня 2011 року землетрус в Хонсю, Японія. (кредит: Даніель Пірс).

    Шкала Ріхтера - це логарифмічна шкала базової десяти. Іншими словами, землетрус магнітудою\(8\) не в два рази більше землетрусу магнітудою\(4\). Це

    \[10^{8−4}=10^4=10,000 \nonumber\]

    раз, як здорово! У цьому уроці ми досліджуємо природу шкали Ріхтера і базову десятку функції, від якої вона залежить.

    Перетворення з логарифмічного в експоненціальну форму

    Для того, щоб проаналізувати величину землетрусів або порівняти величини двох різних землетрусів, нам потрібно вміти конвертувати між логарифмічною та експоненціальною формою. Наприклад, припустимо, кількість енергії, що виділяється від одного землетрусу, було в 500 разів більше, ніж кількість енергії, що виділяється від іншого. Ми хочемо обчислити різницю в величині. Рівняння, яке представляє цю задачу\(10^x=500\), є, де\(x\) представляє різницю величин за шкалою Ріхтера. Як би ми вирішили\(x\)?

    Ми ще не вивчили метод розв'язання експоненціальних рівнянь. Жоден з обговорюваних досі алгебраїчних інструментів не є достатнім для вирішення\(10^x=500\). Ми знаємо, що\({10}^2=100\) і\({10}^3=1000\), отже, зрозуміло, що\(x\) має бути деяке значення між 2 і 3, оскільки\(y={10}^x\) збільшується. Ми можемо вивчити графік, як на малюнку\(\PageIndex{1}\), щоб краще оцінити рішення.

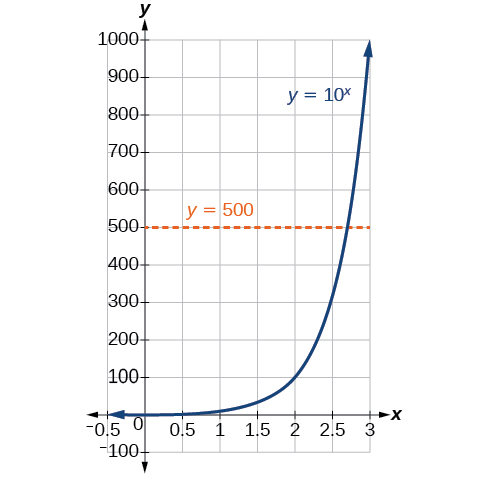
    Графік перетинів рівнянь y=10^x та y=500.

    Малюнок\(\PageIndex{2}\)

    Оцінка за графіком, однак, неточна. Щоб знайти алгебраїчне рішення, ми повинні ввести нову функцію. Зверніть увагу, що графік на малюнку\(\PageIndex{2}\) проходить тест горизонтальної лінії. Експоненціальна функція\(y=b^x\) один до одного, тому її обернена, також\(x=b^y\) є функцією. Як і у випадку з усіма оберненими функціями, ми просто\(x\) обмінюємося\(y\) і вирішуємо для\(y\) пошуку зворотної функції. Щоб представити\(y\) як функцію\(x\), ми використовуємо логарифмічну функцію виду\(y={\log}_b(x)\). Базовий\(b\) логарифм числа - це показник, на який ми повинні підняти,\(b\) щоб отримати це число.

    Ми читаємо логарифмічний вираз як: «Логарифм з\(b\) основою\(x\) дорівнює»\(y\), або, спрощено, «log base\(b\) of\(x\) is»\(y\). Ми також можемо сказати, «\(b\)піднятий до влади\(y\) є»\(x\), тому що журнали є експонентами. Наприклад, базовий\(2\) логарифм\(32\) є\(5\), тому що\(5\) є показником, до якого ми повинні застосувати,\(2\) щоб отримати\(32\). Так як\(2^5=32\), ми можемо писати\({\log}_232=5\). Ми читаємо це як «\(2\)база журналу\(32\) є»\(5\).

    Ми можемо виразити зв'язок між логарифмічною формою та відповідною їй експоненціальною формою наступним чином:

    \[\begin{align} \log_b(x)=y\Leftrightarrow b^y=x, b> 0, b\neq 1 \end{align}\]

    Відзначимо, що база\(b\) завжди позитивна.

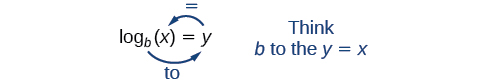
    увійти xx.jpg

    Оскільки логарифм є функцією, він найбільш правильно написаний як\(\log_b(x)\), використовуючи дужки для позначення оцінки функції, так само, як ми б з\(f(x)\). Однак, коли вхідні дані є однією змінною або числом, зазвичай можна побачити, що дужки скинуті, а вираз написаний без дужок, як\(\log_bx\). Зверніть увагу, що багато калькуляторів вимагають дужок навколо\(x\).

    Ми можемо проілюструвати позначення логарифмів наступним чином:

    Зверніть увагу, що, порівнюючи функцію логарифма і експоненціальну функцію, вхід і вихід перемикаються. Це означає\(y={\log}^b(x)\) і\(y=b^x\) є зворотними функціями.

    ВИЗНАЧЕННЯ ЛОГАРИФМІЧНОЇ ФУНКЦІЇ

    Логарифмічна\(b\) база додатного числа\(x\) задовольняє наступному визначенню.

    Для\(x>0\)\(b>0\),\(b≠1\),

    \[\begin{align} y={\log}_b(x)\text{ is equivalent to } b^y=x \end{align}\]

    де,

    • ми читаємо\({\log}_b(x)\) як, «логарифм\(b\) з основою\(x\)» або «\(b\)база журналу»\(x\).
    • логарифм\(y\) - показник, до якого\(b\) потрібно підняти, щоб отримати\(x\).

    Крім того, оскільки логарифмічна та експоненціальна функції перемикають\(y\) значення\(x\) і, область та діапазон експоненціальної функції змінюються місцями для логарифмічної функції. Тому,

    • область функції логарифма з основою\(b\) дорівнює\((0,\infty)\).
    • діапазон функції логарифма з основою\(b\) дорівнює\((−\infty,\infty)\).
    Питання і відповіді: Чи можемо ми взяти логарифм від'ємного числа?

    Ні. Оскільки основа експоненціальної функції завжди позитивна, жодна сила цієї бази ніколи не може бути негативною. Ми ніколи не можемо взяти логарифм від'ємного числа. Крім того, ми не можемо взяти логарифм нуля. Калькулятори можуть виводити журнал від'ємного числа в комплексному режимі, але журнал від'ємного числа не є дійсним числом.

    Як: Задано рівняння в логарифмічній формі\({\log}_b(x)=y\), convert it to exponential form
    1. Вивчіть рівняння\(y={\log}_bx\) і визначити\(b\)\(y\),, і\(x\).
    2. Перепишіть\({\log}_bx=y\) як\(b^y=x\).
    Приклад\(\PageIndex{1}\): Converting from Logarithmic Form to Exponential Form​​​​​​

    Запишіть наступні логарифмічні рівняння в експоненціальному вигляді.

    1. \({\log}_6(\sqrt{6})=\dfrac{1}{2}\)
    2. \({\log}_3(9)=2\)

    Рішення

    Спочатку визначте значення\(b\)\(y\), і\(x\). Потім запишіть рівняння у вигляді\(b^y=x\).

    1. \({\log}_6(\sqrt{6})=\dfrac{1}{2}\)

      Ось,\(b=6\),\(y=\dfrac{1}{2}\), і\(x=\sqrt{6}\). Тому\({\log}_6(\sqrt{6})=\dfrac{1}{2}\) рівняння еквівалентно

      \(6^{\tfrac{1}{2}}=\sqrt{6}\)

    2. \({\log}_3(9)=2\)

      Ось,\(b=3\),\(y=2\), і\(x=9\). Тому\({\log}_3(9)=2\) рівняння еквівалентно

    \(3^2=9\)

    Вправа\(\PageIndex{1}\)

    Запишіть наступні логарифмічні рівняння в експоненціальному вигляді.

    1. \({\log}_{10}(1,000,000)=6\)
    2. \({\log}_5(25)=2\)
    Відповідь на

    \({\log}_{10}(1,000,000)=6\)еквівалентний\({10}^6=1,000,000\)

    Відповідь б

    \({\log}_5(25)=2\)еквівалентний\(5^2=25\)

    Перетворення з експоненціальної в логарифмічну форму

    Щоб перетворити з експонентів в логарифми, ми виконуємо ті ж кроки в зворотному порядку. Ми ідентифікуємо базу\(b\)\(x\), показник і вихід\(y\). Потім пишемо\(x={\log}_b(y)\).

    Приклад\(\PageIndex{2}\): Converting from Exponential Form to Logarithmic Form

    Запишіть наступні експоненціальні рівняння в логарифмічному вигляді.

    1. \(2^3=8\)
    2. \(5^2=25\)
    3. \({10}^{−4}=\dfrac{1}{10,000}\)

    Рішення

    Спочатку визначте значення\(b\)\(y\), і\(x\). Потім запишіть рівняння у вигляді\(x={\log}_b(y)\).

    1. \(2^3=8\)

      Ось,\(b=2\),\(x=3\), і\(y=8\). Тому\(2^3=8\) рівняння еквівалентно\({\log}_2(8)=3\).

    2. \(5^2=25\)

      Ось,\(b=5\),\(x=2\), і\(y=25\). Тому\(5^2=25\) рівняння еквівалентно\({\log}_5(25)=2\).

    3. \({10}^{−4}=\dfrac{1}{10,000}\)

      Ось,\(b=10\),\(x=−4\), і\(y=\dfrac{1}{10,000}\). Тому\({10}^{−4}=\dfrac{1}{10,000}\) рівняння еквівалентно\({\log}_{10} \left (\dfrac{1}{10,000} \right )=−4\).

    Вправа\(\PageIndex{2}\)

    Запишіть наступні експоненціальні рівняння в логарифмічному вигляді.

    1. \(3^2=9\)
    2. \(5^3=125\)
    3. \(2^{−1}=\dfrac{1}{2}\)
    Відповідь на

    \(3^2=9\)еквівалентний\({\log}_3(9)=2\)

    Відповідь б

    \(5^3=125\)еквівалентний\({\log}_5(125)=3\)

    Відповідь c

    \(2^{−1}=\dfrac{1}{2}\)еквівалентний\({\log}_2 \left (\dfrac{1}{2} \right )=−1\)

    Оцінка логарифмів

    Знання квадратів, кубів та коренів чисел дозволяє оцінювати багато логарифмів подумки. Наприклад, розглянемо\({\log}_28\). Ми запитуємо: «До якого\(2\) показника потрібно підняти, щоб отримати 8?» Тому що ми вже знаємо\(2^3=8\), з цього випливає\({\log}_28=3\).

    Тепер розглянемо рішення\({\log}_749\) і\({\log}_327\) подумки.

    • Ми запитуємо: «До якого\(7\) показника потрібно підняти, щоб потрапити\(49\)?» Ми знаємо\(7^2=49\). Тому,\({\log}_749=2\)
    • Ми запитуємо: «До якого\(3\) показника потрібно підняти, щоб потрапити\(27\)?» Ми знаємо\(3^3=27\). Тому,\(\log_{3}27=3\)

    Навіть деякі, здавалося б, більш складні логарифми можна оцінити без калькулятора. Наприклад, давайте оцінимо\(\log_{\ce{2/3}} \frac{4}{9}\) подумки.

    • Ми запитуємо: «До якого\(\ce{2/3}\) показника потрібно підняти, щоб потрапити\(\ce{4/9}\)? » Ми знаємо\(2^2=4\) і\(3^2=9\),\[{\left(\dfrac{2}{3} \right )}^2=\dfrac{4}{9}. \nonumber\] отже,\[{\log}_{\ce{2/3}} \left (\dfrac{4}{9} \right )=2. \nonumber\]
    Як: Задано логарифм виду\(y={\log}_b(x)\),evaluate it mentally
    1. Перепишіть аргумент\(x\) як силу\(b\):\(b^y=x\).
    2. Використовуйте попередні знання про повноваження\(b\) ідентифікації, запитуючи: «\(y\)До якого показника\(b\) слід підняти, щоб отримати\(x\)?»
    Приклад\(\PageIndex{3}\): Solving Logarithms Mentally

    Вирішіть\(y={\log}_4(64)\) без використання калькулятора.

    Рішення

    Спочатку перепишемо логарифм в експоненціальному вигляді:\(4^y=64\). Далі ми запитуємо: «До якого показника потрібно\(4\) підняти, щоб потрапити\(64\)?»

    Ми знаємо

    \(4^3=64\)

    Тому,

    \({\log}_4(64)=3\)

    Вправа\(\PageIndex{3}\)

    Вирішіть\(y={\log}_{121}(11)\) без використання калькулятора.

    Відповідь

    \({\log}_{121}(11)=\dfrac{1}{2}\)(нагадуючи, що\(\sqrt{121}={(121)}^{\tfrac{1}{2}}=11)\)

    Приклад\(\PageIndex{4}\): Evaluating the Logarithm of a Reciprocal

    Оцінюйте\(y={\log}_3 \left (\dfrac{1}{27} \right )\) без використання калькулятора.

    Рішення

    Спочатку перепишемо логарифм в експоненціальному вигляді:\(3^y=\dfrac{1}{27}\). Далі ми запитуємо: «До якого показника потрібно\(3\) підняти, щоб потрапити\(\dfrac{1}{27}\)?»

    Ми знаємо\(3^3=27\), але що ми повинні зробити, щоб отримати відповідь,\(\dfrac{1}{27}\)? Нагадаємо з роботи з експонентами, що\(b^{−a}=\dfrac{1}{b^a}\). Ми використовуємо цю інформацію для написання

    \[\begin{align*} 3^{-3}&= \dfrac{1}{3^3}\\ &= \dfrac{1}{27} \end{align*}\]

    Тому,\({\log}_3 \left (\dfrac{1}{27} \right )=−3\).

    Вправа\(\PageIndex{4}\)

    Оцінюйте\(y={\log}_2 \left (\dfrac{1}{32} \right )\) без використання калькулятора.

    Відповідь

    \({\log}_2 \left (\dfrac{1}{32} \right )=−5\)

    Використання загальних логарифмів

    Іноді ми можемо побачити логарифм, написаний без основи. В даному випадку припускаємо, що основа є\(10\). Іншими словами, вираз\(\log(x)\) означає\({\log}_{10}(x)\). Базовий\(-10\) логарифм ми називаємо загальним логарифмом. Загальні логарифми використовуються для вимірювання шкали Ріхтера, згаданої на початку розділу. Шкали для вимірювання яскравості зірок і рН кислот і підстав також використовують загальні логарифми.

    ВИЗНАЧЕННЯ ЗАГАЛЬНОГО ЛОГАРИФМА

    Загальний логарифм - логарифм з підставою\(10\). Пишемо\({\log}_{10}(x)\) просто як\(\log(x)\). Загальний логарифм додатного числа\(x\) задовольняє наступному визначенню.

    Для\(x>0\),

    \[\begin{align} y={\log}(x)\text{ is equivalent to } {10}^y=x \end{align}\]

    Ми читаємо\(\log(x)\) як, «логарифм з\(10\) основою\(x\)» або «бревна\(10\) база»\(x\).

    Логарифм\(y\) - це показник, до якого\(10\) потрібно підняти, щоб отримати\(x\).

    Як: Задано загальний логарифм виду\(y=\log(x)\), evaluate it mentally
    1. Перепишіть аргумент\(x\) як силу\(10\):\({10}^y=x\).
    2. Використовуйте попередні знання про повноваження,\(10\) щоб ідентифікувати, запитуючи: «\(y\)До якого показника потрібно\(10\) підняти, щоб отримати\(x\)?»
    Приклад\(\PageIndex{5}\): Finding the Value of a Common Logarithm Mentally

    Оцінюйте\(y=\log(1000)\) без використання калькулятора.

    Рішення

    Спочатку перепишемо логарифм в експоненціальному вигляді:\({10}^y=1000\). Далі ми запитуємо: «До якого показника потрібно\(10\) підняти, щоб потрапити\(1000\)?» Ми знаємо

    \({10}^3=1000\)

    Тому,\(\log(1000)=3\).

    Вправа\(\PageIndex{5}\)

    Оцініть\(y=\log(1,000,000)\).

    Відповідь

    \(\log(1,000,000)=6\)

    Як: Задано загальний логарифм з формою\(y=\log(x)\),evaluate it using a calculator
    1. Натисніть [LOG].
    2. Введіть значення, задане для\(x\), а потім [)].
    3. Натисніть [ENTER].
    Приклад\(\PageIndex{6}\): ​​​​​​Finding the Value of a Common Logarithm Using a Calculator

    Оцініть\(y=\log(321)\) до чотирьох знаків після коми за допомогою калькулятора.

    Рішення

    • Натисніть [LOG].
    • Введіть 321, а потім [)].
    • Натисніть [ENTER].

    Округлення до чотирьох знаків після коми,\(\log(321)≈2.5065\).

    Аналіз

    Зверніть увагу, що\({10}^2=100\) і те\({10}^3=1000\). Оскільки\(321\) знаходиться між\(100\) і\(1000\), ми знаємо, що\(\log(321)\) повинно бути між\(\log(100)\) і\(\log(1000)\). Це дає нам наступне:

    \(100<321<1000\)

    \(2<2.5065<3\)

    Вправа\(\PageIndex{6}\)

    Оцініть\(y=\log(123)\) до чотирьох знаків після коми за допомогою калькулятора.

    Відповідь

    \(\log(123)≈2.0899\)

    Приклад\(\PageIndex{7}\): Rewriting and Solving a Real-World Exponential Model

    Кількість енергії, що виділяється від одного землетрусу, було в\(500\) рази більше, ніж кількість енергії, що виділяється від іншого. Рівняння\({10}^x=500\) представляє таку ситуацію,\(x\) де різниця величин за шкалою Ріхтера. До найближчої тисячної, яка була різниця в величинях?

    Рішення

    Почнемо з перезапису експоненціального рівняння в логарифмічному вигляді.

    \({10}^x=500\)

    \(\log(500)=x\)Скористайтеся визначенням загального журналу.

    Далі оцінюємо логарифм за допомогою калькулятора:

    • Натисніть [LOG].
    • Введіть\(500\), а потім [)].
    • Натисніть [ENTER].
    • До найближчої тисячної,\(\log(500)≈2.699\).

    Різниця в величині була приблизно\(2.699\).

    Вправа\(\PageIndex{7}\)

    Кількість енергії, що виділяється від одного землетрусу, було в\(8,500\) рази більше, ніж кількість енергії, що виділяється від іншого. Рівняння\({10}^x=8500\) представляє таку ситуацію,\(x\) де різниця величин за шкалою Ріхтера. До найближчої тисячної, яка була різниця в величинях?

    Відповідь

    Різниця в величині була приблизно\(3.929\).

    Використання природних логарифмів

    Найбільш часто використовуваною базою для логарифмів є\(e\). Базові\(e\) логарифми важливі в обчисленні та деяких наукових додатках; їх називають природними логарифмами. Базовий\(e\) логарифм\({\log}_e(x)\),, має свої позначення,\(\ln(x)\). Більшість значень\(\ln(x)\) можна знайти тільки за допомогою калькулятора. Основним винятком є те, що, тому що логарифм завжди\(1\) знаходиться\(0\) в будь-якій базі,\(\ln1=0\). Для інших природних логарифмів ми можемо використовувати\(\ln\) ключ, який можна знайти на більшості наукових калькуляторів. Ми також можемо знайти натуральний логарифм будь-якої потужності,\(e\) використовуючи обернену властивість логарифмів.

    ВИЗНАЧЕННЯ НАТУРАЛЬНОГО ЛОГАРИФМА

    Натуральний логарифм - це логарифм з підставою\(e\). Пишемо\({\log}_e(x)\) просто як\(\ln(x)\). Натуральний логарифм додатного числа\(x\) задовольняє наступному визначенню.

    Для\(x>0\),

    \(y=\ln(x)\)еквівалентний\(e^y=x\)

    Ми читаємо\(\ln(x)\) як, «логарифм з\(e\) основою\(x\)» або «натуральний логарифм»\(x\).

    Логарифм\(y\) - це показник, до якого\(e\) потрібно підняти, щоб отримати\(x\).

    Так як функції\(y=e^x\) і\(y=\ln(x)\) є зворотними функціями,\(\ln(e^x)=x\) для всіх\(x\) і\(e^{\ln (x)}=x\) для\(x>0\).

    Як: Задано натуральний логарифм з формою\(y=\ln(x)\), evaluate it using a calculator
    1. Натисніть [LN].
    2. Введіть значення, задане для\(x\), а потім [)].
    3. Натисніть [ENTER].
    Приклад\(\PageIndex{8}\): Evaluating a Natural Logarithm Using a Calculator

    Оцініть\(y=\ln(500)\) до чотирьох знаків після коми за допомогою калькулятора.

    Рішення

    • Натисніть [LN].
    • Введіть\(500\), а потім [)].
    • Натисніть [ENTER].

    Округлення до чотирьох знаків після коми,\(\ln(500)≈6.2146\)

    Вправа\(\PageIndex{8}\)

    Оцініть\(\ln(−500)\).

    Відповідь

    Неможливо взяти логарифм від'ємного числа в множині дійсних чисел.

    Медіа

    Отримайте доступ до цього інтернет-ресурсу для додаткової інструкції та практики з логарифмами.

    Ключові рівняння

    Визначення логарифмічної функції Для\(x>0\),\(b>0\)\(b≠1\),\(y={\log}_b(x)\) якщо і тільки якщо\(b^y=x\).
    Визначення загального логарифма Для\(x>0\),\(y=\log(x)\) якщо і тільки якщо\({10}^y=x\).
    Визначення натурального логарифма Для\(x>0\),\(y=\ln(x)\) якщо і тільки якщо\(e^y=x\).

    Ключові концепції

    • Обернена експоненціальна функція є логарифмічною функцією, а оберненою логарифмічною функцією є експоненціальна функція.
    • Логарифмічні рівняння можна записати в еквівалентній експоненціальній формі, використовуючи визначення логарифма. Див\(\PageIndex{1}\). Приклад.
    • Експоненціальні рівняння можуть бути записані в їх еквівалентній логарифмічній формі за допомогою визначення логарифма Див\(\PageIndex{2}\). Приклад.
    • Логарифмічні функції з базою\(b\) можуть бути оцінені подумки, використовуючи попередні знання степеней\(b\). Див. Приклад\(\PageIndex{3}\) і Приклад\(\PageIndex{4}\).
    • Загальні логарифми можна оцінити подумки, використовуючи попередні знання про повноваження\(10\). Див\(\PageIndex{5}\). Приклад.
    • Коли загальні логарифми не можуть бути оцінені подумки, можна використовувати калькулятор. Див\(\PageIndex{6}\). Приклад.
    • Реальні експоненціальні задачі з базою\(10\) можуть бути переписані як загальний логарифм, а потім оцінені за допомогою калькулятора. Див\(\PageIndex{7}\). Приклад.
    • Природні логарифми можна оцінити за допомогою калькулятора Приклад\(\PageIndex{8}\).

    Автори та атрибуція