10.11: Іспит з кваліфікації

Last updated
Save as PDF

Page ID: 58508

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Іспит з кваліфікації

Для квадратичних рівнянь у наступних задачах вкажіть значення$a, b$, і$c$.

Вправа$\PageIndex{1}$

$2y^2 - 3y + 10 = 0$

Відповідь: $a=2,b=−3,c=10$

Вправа$\PageIndex{2}$

$10b^2 = 3b$

Відповідь: $a=10,b=−3,c=0$

Для наступних задач використовуйте властивість нульового фактора для вирішення кожного квадратного рівняння.

Вправа$\PageIndex{3}$

$(3x+5)(x−1)=0$

Відповідь: $x = -\dfrac{5}{3}, 1$

Вправа$\PageIndex{4}$

$3b(2b−1)=0$

Відповідь: $b = 0, \dfrac{1}{2}$

Вправа$\PageIndex{5}$

$(a - 8)^2 = 0$

Відповідь: $a=8$

Для наступних задач вирішуйте кожне квадратне рівняння методом факторингу.

Вправа$\PageIndex{6}$

$4x^2 - 16 = 0$

Відповідь: $x=−2,2$

Вправа$\PageIndex{7}$

$y^2 - 12y + 32 = 0$

Відповідь: $y=4,8$

Вправа$\PageIndex{8}$

$a^2 - 5a = 14$

Відповідь: $−2,7$

Вправа$\PageIndex{9}$

$6a^2 = 10 - 11a$

Відповідь: $a = -\dfrac{5}{2}, \dfrac{2}{3}$

Вправа$\PageIndex{10}$

$2x^2 = -2 - 5x$

Відповідь: $x = -2, -\dfrac{1}{2}$

Вправа$\PageIndex{11}$

$x^3 - 25x = 0$

Відповідь: $x=0,−5,5$

Для наступних задач вирішуйте кожне квадратне рівняння шляхом вилучення коренів.

Вправа$\PageIndex{12}$

$c^2 = 81$

Відповідь: $c=−9,9$

Вправа$\PageIndex{13}$

$x^2 = 15$

Відповідь: $x = -\sqrt{15}, \sqrt{15}$

Вправа$\PageIndex{14}$

$3a^2 - 18 = 0$

Відповідь: $a = -\sqrt{6}, \sqrt{6}$

Вправа$\PageIndex{15}$

$(x - 5)^2 = 1$

Відповідь: $x=4,6$

Вправа$\PageIndex{16}$

$(y + 11)^2 - 9 = 0$

Відповідь: $y=−8,−14$

Вправа$\PageIndex{17}$

$y^2 - 25z^2 = 0$для$y$.

Відповідь: $y=−5z,5z$

Вправа$\PageIndex{18}$

$6a^2 - 18b^2c^2$для$a$

Відповідь: $a = \pm bc\sqrt{3}$

Для наступних задач вирішуйте кожне квадратне рівняння за квадратичною формулою.

Вправа$\PageIndex{19}$

$x^2 - 6x - 16 = 0$

Відповідь: $x=−2,8$

Вправа$\PageIndex{20}$

$y^2 - 2y - 7 = 0$

Відповідь: $y = 1 + 2\sqrt{2}$

Вправа$\PageIndex{21}$

$(m + 2)^2 - 5 = 0$

Відповідь: $m = -2 \pm \sqrt{5}$

Вправа$\PageIndex{22}$

$(x + b)^2 = c^2$

Відповідь: $x = -b \pm c$

Вправа$\PageIndex{23}$

$(x+1)(x+4)=6$

Відповідь: $x = \dfrac{-5 \pm \sqrt{33}}{2}$

Вправа$\PageIndex{24}$

$5z^2 - 5z - 5 = 2z^2 - z$

Відповідь: $z = \dfrac{2 \pm \sqrt{19}}{3}$

Вправа$\PageIndex{25}$

$2m^2 = 5m$

Відповідь: $m = 0, \dfrac{5}{2}$

Для наступних задач вирішуйте кожне квадратне рівняння, заповнивши квадрат.

Вправа$\PageIndex{26}$

$x^2 + 6x - 8 = 0$

Відповідь: $x = -3 \pm \sqrt{17}$

Вправа$\PageIndex{27}$

$2x^2 + 7x - 12 = 0$

Відповідь: $x = \dfrac{-7 \pm \sqrt{145}}{4}$

Вправа$\PageIndex{28}$

Добуток двох послідовних непарних цілих чисел 143. Які вони бувають?

Відповідь: 11 і 13 або −11 і −13

Вправа$\PageIndex{29}$

Дослідження якості повітря екологічною групою свідчить про те, що через t років рівень окису вуглецю в повітрі, в частках на мільйон, буде задаватися квадратним рівнянням.

$A = 0.4t^2 + 0.1t + 3.1$

де$A$ представляє кількість чадного газу в повітрі.

а) Який зараз рівень чадного газу в повітрі частинами на мільйон?

б) Через скільки років буде рівень чадного газу на рівні 18,1 частини на мільйон?

Відповідь

(а) 3.1

(b) 6 років від тепер

Вправа$\PageIndex{30}$

Довжина прямокутника на 6 дюймів більше ширини прямокутника. Знайдіть розміри прямокутника, якщо площа становить 112 квадратних футів.

Відповідь

ширина:$\dfrac{-1 + \sqrt{1793}}{4}$

довжина:$\dfrac{1 + \sqrt{1793}}{4}$

Для наступних задач побудуйте графіки наступних рівнянь.

Вправа$\PageIndex{31}$

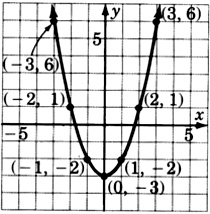
$y = x^2 - 3$

$Координатна площина xy з лініями сітки, позначена негативними п'ятьма і п'ятьма з кроком в одну одиницю на обох осях.$

Відповідь: $Графік параболи, що проходить через сім точок з координатами від'ємні три, шість; негативні два, один; негативний один, негативний два; нуль, негативні три; один, від'ємний два; два, один; і три, шість.$

Вправа$\PageIndex{32}$

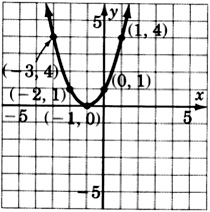
$y = (x + 1)^2$

Відповідь: $Графік параболи, що проходить через п'ять точок з координатами від'ємні три, чотири; негативні два, один; негативний один, нуль; нуль, один; і один, чотири.$

Вправа$\PageIndex{33}$

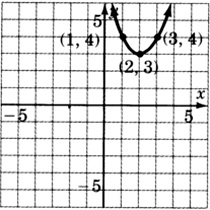
$y = (x-2)^2 + 3$

Відповідь: $Графік параболи, що проходить через три точки з координатами один, чотири; два, три; і три, чотири.$

Для наступних задач напишіть рівняння, яке відповідає кожному графу.

Вправа$\PageIndex{34}$

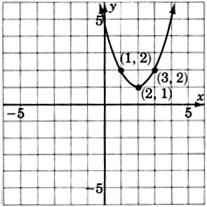
$Графік квадратного рівняння, що проходить через три точки з координатами один, два; два, один; і три, два.$

Відповідь: $y = (x-2)^2 + 1$або$y = x^2 - 4x + 5$

Вправа$\PageIndex{35}$

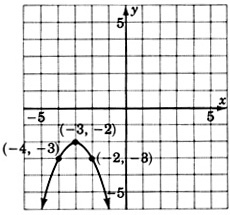
$Графік квадратного рівняння, що проходить через три точки з координатами від'ємні чотири, від'ємні три; негативні три, негативні два; і негативні два, негативні три.$

Відповідь: $y = -(x + 3)^2 - 2$або$y = -x^2 - 6x - 11$

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Вправа\(\PageIndex{3}\)

Вправа\(\PageIndex{4}\)

Вправа\(\PageIndex{5}\)

Вправа\(\PageIndex{6}\)

Вправа\(\PageIndex{7}\)

Вправа\(\PageIndex{8}\)

Вправа\(\PageIndex{9}\)

Вправа\(\PageIndex{10}\)

Вправа\(\PageIndex{11}\)

Вправа\(\PageIndex{12}\)

Вправа\(\PageIndex{13}\)

Вправа\(\PageIndex{14}\)

Вправа\(\PageIndex{15}\)

Вправа\(\PageIndex{16}\)

Вправа\(\PageIndex{17}\)

Вправа\(\PageIndex{18}\)

Вправа\(\PageIndex{19}\)

Вправа\(\PageIndex{20}\)

Вправа\(\PageIndex{21}\)

Вправа\(\PageIndex{22}\)

Вправа\(\PageIndex{23}\)

Вправа\(\PageIndex{24}\)

Вправа\(\PageIndex{25}\)

Вправа\(\PageIndex{26}\)

Вправа\(\PageIndex{27}\)

Вправа\(\PageIndex{28}\)

Вправа\(\PageIndex{29}\)

Вправа\(\PageIndex{30}\)

Вправа\(\PageIndex{31}\)

Вправа\(\PageIndex{32}\)

Вправа\(\PageIndex{33}\)

Вправа\(\PageIndex{34}\)

Вправа\(\PageIndex{35}\)