10.8: Графічні квадратичні рішення

Параболи

Зараз ми вивчимо графіки квадратичних рівнянь у двох змінних із загальною формою

$y = ax^2 + bx + c, a \not= 0$. $a, b, c$є дійсними числами.

Парабола

Всі такі графіки мають схожу форму. Графік квадратного рівняння цього типу Парабола називається параболою і він буде приймати одну з наступних форм.

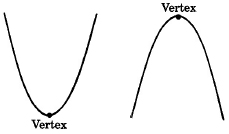
Вершина

Висока точка або низька точка параболи називається вершиною параболи.

Побудова графіків парабол

Ми побудуємо графік параболи, вибравши кілька значень x, обчисливши, щоб знайти відповідні значення y, побудувавши ці впорядковані пари, а потім проведемо гладку криву через них.

Набір зразків A

Приклад$\PageIndex{1}$

Графік$y = x^2$. Побудувати таблицю, щоб виставити кілька впорядкованих пар.

$x$	$y=x^2$
0	0
1	1
2	4
3	9
−1	1
−2	4
−3	9

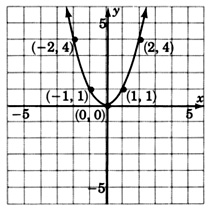
Це найголовніша парабола. Хоча інші параболи можуть бути ширшими, вужчими, переміщеними вгору або вниз, переміщеними вліво або вправо, або перевернутими, всі вони матимуть ту саму основну форму. Нам потрібно буде побудувати стільки впорядкованих пар, скільки необхідно, щоб забезпечити цю основну форму.

Приклад$\PageIndex{2}$

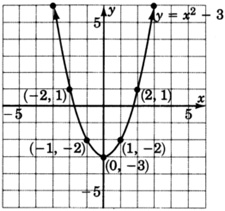
Графік$y = x^2 - 2$. Побудувати таблицю впорядкованих пар.

$x$	$y=x^2 -2$
0	−2
1	−1
2	2
3	7
−1	−1
−2	2
−3	7

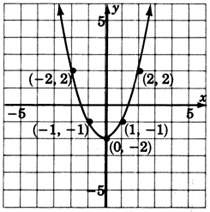
Зверніть увагу, що графік$y = x^2 - 2$ - це саме графік,$y = x^2$ але перекладено 2 одиниці вниз. Порівняйте рівняння$y = x^2$ і$y = x^2 - 2$. Ви бачите, що викликає 2 одиниці низхідного перекладу?

Практика Set A

Завдання практики$\PageIndex{1}$

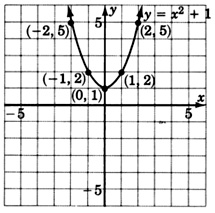
Використовуйте ідею, запропоновану в наборі зразків A, щоб намалювати (швидко і, можливо, не зовсім точно) графіки

$y = x^2 + 1$і$y = x^2 - 3$

Відповідь

Набір зразків B

Приклад$\PageIndex{1}$

Графік$y = (x + 2)^2$.

Чи очікуємо ми, що графік буде схожий на графік$y = x^2$? Складіть таблицю упорядкованих пар.

$x$	$y$
0	4
1	9
−1	1
−2	0
−3	1
−4	4

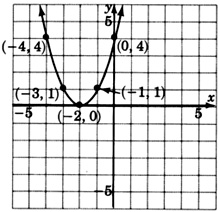
Зверніть увагу, що графік$y = (x + 2)^2$ є саме графіком,$y = x^2$ але перекладено 2 одиниці ліворуч. $+2$Внутрішня частина дужок переміщує$y = x^2$ дві одиниці вліво. Від'ємне значення всередині дужок робить рух вправо.

Практика Set B

Завдання практики$\PageIndex{1}$

Використовуйте ідею, запропоновану в наборі зразків B, щоб намалювати графіки

$y = (x-3)^2$і$y = (x + 1)^2$

Відповідь

Завдання практики$\PageIndex{3}$

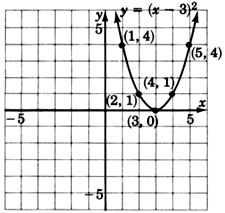
Графік$y = (x-2)^2 + 1$

Відповідь

Вправи

Для наступних задач графуйте квадратні рівняння.

Вправа$\PageIndex{1}$

$y = x^2$

Відповідь

Вправа$\PageIndex{2}$

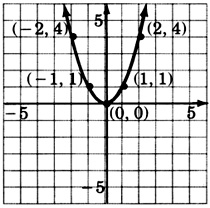
$y = -x^2$

Вправа$\PageIndex{3}$

$y = (x-1)^2$

Відповідь

Вправа$\PageIndex{4}$

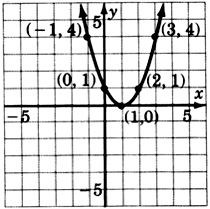
$y = (x-2)^2$

Вправа$\PageIndex{5}$

$y = (x + 3)^2$

Вправа$\PageIndex{6}$

$y = (x + 3)^2$

Відповідь

Вправа$\PageIndex{7}$

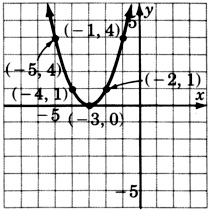
$y = (x + 1)^2$

Вправа$\PageIndex{8}$

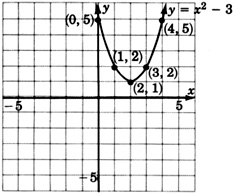
$y = x^2 - 3$

Відповідь

Вправа$\PageIndex{9}$

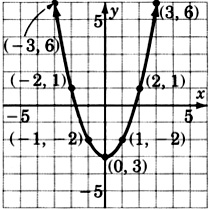
$y = x^2 - 1$

Вправа$\PageIndex{10}$

$y = x^2 + 2$

Відповідь

Вправа$\PageIndex{11}$

$y = x^2 + \dfrac{1}{2}$

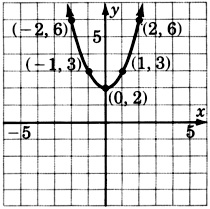
Вправа$\PageIndex{12}$

$y = x^2 - \dfrac{1}{2}$

Відповідь

Вправа$\PageIndex{13}$

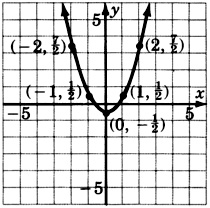
$y = -x^2 + 1$(порівняти з проблемою 2)

Вправа$\PageIndex{14}$

$y = -x^2 - 1$(порівняти з проблемою 1)

Відповідь

Вправа$\PageIndex{15}$

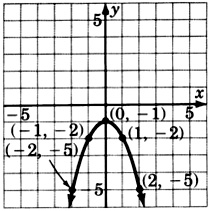
$y = (x-1)^2 - 1$

Вправа$\PageIndex{16}$

$y = (x + 3)^2 + 2$

Відповідь

Вправа$\PageIndex{17}$

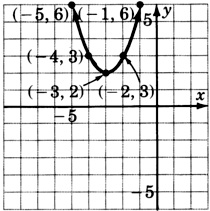
$y = -(x + 1)^2$

Вправа$\PageIndex{18}$

$y = -(x + 3)^2$

Відповідь

Вправа$\PageIndex{19}$

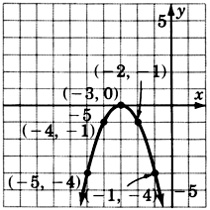
$y = 2x^2$

Вправа$\PageIndex{20}$

$y = 3x^2$

Відповідь

Вправа$\PageIndex{21}$

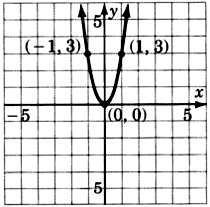
$y = \dfrac{1}{2}x^2$

Для наступних задач спробуйте вгадати квадратне рівняння, яке відповідає заданому графіку.

Вправа$\PageIndex{22}$

Вправа$\PageIndex{23}$

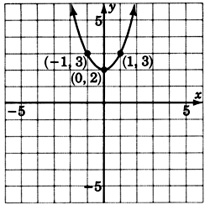
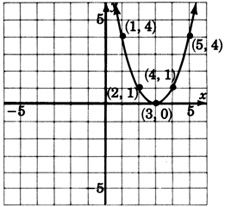
Відповідь

$y = (x-3)^2$

Вправа$\PageIndex{24}$

Вправа$\PageIndex{25}$

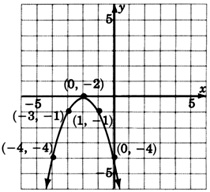
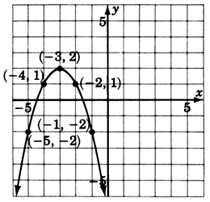
Відповідь

$y = -(x + 3)^2 + 2$

Вправи для огляду

Вправа$\PageIndex{26}$

Спростити і написати$(x^{-4}y^5)^{-3}(x^{-6}y^4)^2$ так, щоб з'являлися тільки позитивні показники.

Вправа$\PageIndex{27}$

Фактор$y^2 - y - 42$

Відповідь

$(y+6)(y−7)$

Вправа$\PageIndex{28}$

Знайдіть суму:$\dfrac{2}{a - 3} + \dfrac{3}{a + 3} + \dfrac{18}{a^2 - 9}$

Вправа$\PageIndex{29}$

Спростити$\dfrac{2}{4 + \sqrt{5}}$

Відповідь

$\dfrac{8 - 2\sqrt{5}}{11}$

Вправа$\PageIndex{30}$

Чотири додається до цілого числа і ця сума подвоюється. Коли цей результат множиться на початкове ціле число, добуток дорівнює$-6$. Знайдіть ціле число.