10.7: Додатки

П'ятиступінчастий метод

Зараз ми в змозі вивчити деякі застосування квадратних рівнянь. Квадратичні рівняння можуть виникати з безлічі фізичних (прикладних) і математичних (логічних) задач.

Ми, знову ж таки, застосуємо п'ятикроковий метод для вирішення проблем слів.

П'ятикроковий метод вирішення проблем слів

• Крок 1: Нехай$x$ (або якась інша буква) представляють невідому кількість.
• Крок 2: Переведіть словесний вираз на математичні символи і сформуйте рівняння.
• Крок 3: Вирішіть це рівняння.
• Крок 4: Перевірте рішення, підставивши результат у рівняння, знайдене на кроці 2.
• Крок 5: Напишіть висновок.

Пам'ятайте, крок 1 дуже важливий.

Примітка

Завжди починайте з введення змінної

Як тільки квадратне рівняння розроблено (крок 2), спробуйте вирішити його шляхом факторингу. Якщо факторинг не працює, використовуйте квадратичну формулу. Калькулятор може допомогти зробити деякі розрахунки трохи менш виснажливими.

Набір зразків A

Приклад$\PageIndex{1}$

Виробник чохлів для миші для персональних комп'ютерів визначає, що$N$ кількість проданих обкладинок пов'язана$x$ з ціною обкладинки$N = 35x - x^2$. За якою ціною виробник повинен цінувати миша, щоб їх$216$ продати.

\ (\ begin {масив} {flushleft}
\ text {Крок 1:} &\ text {Нехай} x=\ текст {ціна обкладинки миші.} \\
\ текст {Крок 2:} &\ текст {Оскільки} N\ текст {має бути} 216\ текст {рівняння}\\
& 216 = 35x - x^2\ end {масив}
\)\ (
\ begin {масив} {Flushleft}
\ text {Крок 3:} & 216 &= 35x - x^2 &\ text {Переписати в стандартному вигляді}\\
& x^2 - 35x + 216 &= 0 &\ text {Спробуйте факторинг.}\\
& (x-8) (x-27) &= 0\\
& x-8 = 0 &\ текст {або} x-27=0\\
& x = 8 &\ text {або} x = 27
\ end {масив}\)
Перевірте цей потенціал рішення.
\ (\ begin {масив} {Flushleft}
\ текст {Крок 4:} &\ текст {Якщо} x = 8, & &\ текст {Якщо} x = 27\\
& 35\ cdot 8 &= 216 &\ text {Це правильно? } & 35\ cdot 27 - 27^2 &= 216 &\ текст {Це правильно? }\\
& 280 - 64 &= 216 &\ текст {Це правильно? } & 945 - 729 &= 216 &\ текст {Це правильно? }\\
& 216 &= 216 &\ text {Так, це правильно.} & 216 &= 216 &\ text {Так, це правильно.}\
\ end {масив}\)
Ці рішення перевіряють.

Крок 5: Кришки комп'ютерної миші можуть коштувати $8 або $27, щоб продати 216 з них.

Практика Set A

Завдання практики$\PageIndex{1}$

Виробник тканинних пилозахисних чохлів персонального комп'ютера зауважує, що$N$ кількість проданих чохлів пов'язано з ціною чохлів по$N = 30x - x^2$. За якою ціною виробник повинен цінувати чохли, щоб їх$216$ продати?

Крок 1:


Крок 2:


Крок 3:




Крок 4:




Крок 5: Для того, щоб продаємо 216 чохлів, виробник повинен їх ціну в будь-якому або.

Відповідь

12 або 18

Завдання практики$\PageIndex{2}$

$t$Підраховано, що через роки населення конкретного міста буде

$P = t^2 - 24t + 96000$

Через скільки років буде населення на 95 856?

Крок 1:


Крок 2:


Крок 3:




Крок 4:




Крок 5:

Відповідь

У 9 і 15 років населення міста становитиме 95 865.

Набір зразків B

Приклад$\PageIndex{2}$

Довжина прямокутника на 4 дюйми більше, ніж в два рази більше ширини. Площа складає 30 квадратних дюймів. Знайдіть розміри (довжину і ширину).

Крок 1: Нехай$x=$ ширина. Потім$2x + 4 =$, довжина.

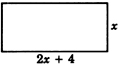
Крок 2: Площа a визначається як довжина прямокутника на ширину прямокутника. Таким чином,
$x(2x + 4) = 30$

\ (\ begin {масив} {Flushleft}
\ текст {Крок 3:} & x (2x + 4) &= 30\\
& 2x^2 + 4x &= 30\\
& 2x^2 + 4x - 30 &= 0 &\\ текст {Розділити кожну сторону на} 2\\
x ^ 2x - 15 &= 0 &\\ текст {Фактор.}\\
& (x+5) (х-3) &= 0
& x &= -5, 3\\
& x & -5 &\ text {не має фізичного значення, тому ми ігноруємо його. Перевірка} x = 3\\
& x &= 3
\ end {масив}\)
$2x + 4 = 2 \cdot 3 + 4 = 10$

\ (\ begin {масив} {Flushleft}
\ текст {Крок 4:} & x (2x + 4) &= 30 &\ text {Це правильно?} \\
& 3 (2\ cdot 3 + 4) &= 30 &\ текст {Це правильно?} \\
& 3 (6 + 4) &= 30 &\ текст {Це правильно?} \\
& 3 (10) &= 30 &\ текст {Це правильно?} \\
& 30 &= 30 &\ текст {Так, це правильно}
\ end {масив}\)

Крок 5: Ширина$= 3$ дюймів і довжина$= 10$ дюймів.

Практика Set B

Завдання практики$\PageIndex{3}$

Довжина прямокутника на 3 фути більше, ніж удвічі більше ширини. Площа становить 14 квадратних футів. Знайдіть розміри.

Відповідь

ширина = 2 фути, довжина = 7 футів

Завдання практики$\PageIndex{4}$

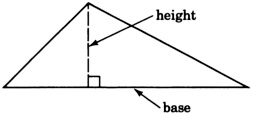
Площа трикутника становить 24 квадратних метра. Підстава на 2 метри довше висоти. Знайдіть підставу і висоту. Формула для площі трикутника така$A = \dfrac{1}{2} b \cdot h$.

Відповідь

висота = 6 метрів, підстава = 8 метрів

Набір зразків C

Приклад$\PageIndex{3}$

Добуток двох послідовних цілих чисел дорівнює 156. Знайдіть їх

\ (\ begin {масив} {flushleft}
\ text {Крок 1:} &\ text {Нехай} x &=\ текст {менше ціле число.} \\
& x + 1 &=\ текст {наступне ціле число}\
\ текст {Крок 2:} x (x + 1) &= 156\
\\ текст {Крок 3:} x (x + 1) &= 156\\
& x^2+ x = 156\\
x - 156 &= 0\\
& (x-12) (x - 13) &= 0\\
& x &= 12, -13
\ кінець {масив}\)

Цю факторизацію може бути важко здогадатися. Ми також могли б використовувати квадратичну формулу.

\ (\ begin {масив} {Flushleft}
\ текст {Крок 4:} &\ текст {Якщо} x=12: & 12 (2 + 1) &= 156 &\ text {Це правильно?} \\
& & 12 (13) &= 156 &\ текст {Це правильно?} \\
& & 156 &= 156 &\ текст {Так, це правильно}\\
&\ текст {Якщо} x = -13 & -13 (-13 + 1) &= 156 &\ text {Це правильно?} \\
& & -13 (-12) &= 156 &\ текст {Це правильно?} \\
& & 156 &= 156 &\ текст {Так, це правильно.}
\ end {масив}\)

Крок 5: Є два рішення:$12, 13$, і$-13, -12$

Практика Set C

Завдання практики$\PageIndex{5}$

Добуток двох послідовних цілих чисел дорівнює 210. Знайдіть їх.

Відповідь

14 і 15, і —14 і —15

Завдання практики$\PageIndex{6}$

Чотири додається до цілого числа, і ця сума збільшується втричі. Коли цей результат множиться на початкове ціле число, добуток буде −12. Знайдіть ціле число.

Відповідь

—2

Набір зразків D

Приклад$\PageIndex{4}$

Коробка без верху і квадратної основи повинна бути виготовлена шляхом вирізання 2-дюймових квадратів з кожного кута і складання сторін шматка квадратного картону. Обсяг коробки повинен бути 8 кубічних дюймів. Якого розміру повинен бути шматок картону?

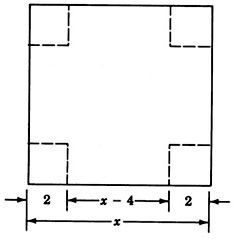
Крок 1: Нехай$x=$ довжина (і ширина) шматка картону.

Крок 2: Обсяг прямокутної коробки дорівнює

$V = \text{(length) (width) (height)}$
$8 = (x-4)(x-4)2$

\ (\ почати {масив} {Flushleft}
\ текст {Крок 3:} & 8 = (х-4) (х-4) 2\\
& 8 = (x^2 - 8x + 16) 2\\
& 8 = 2x^2 - 16x + 32\
& 2x^2 - 16x + 24 = 0 &\ текст {Розділити кожну сторону на} 2\\
& x^2 - 8x + 12 = 0 &\ текст {Фактор.} \\
& (x-6) (x-2) = 0
& x = 6, 2
\ end {масив}\)

$x$не може рівнятися$2$ (розріз пройшов би через шматок картону). Перевірте$x = 6$.

\ (\ begin {масив} {Flushleft}
\ текст {Крок 4:} & (6 - 4) (6 - 4) 2 &= 8 &\ текст {Чи правильно це?} \\
& (2) (2) 2 &= 8 &\ text {Це правильно?} \\
& 8&=8 &\ text {Так, це правильно.}
\ end {масив}\)

Крок 5: Шматок картону повинен бути 6 дюймів на 6 дюймів.

Практика Set D

Завдання практики$\PageIndex{7}$

Коробка без верху і квадратної основи повинна бути виготовлена шляхом вирізання 3-дюймових квадратів з кожного кута і складання сторін шматочка картону. Обсяг коробки повинен бути 48 кубічних дюймів. Якого розміру повинен бути шматок картону?

Відповідь

10 в. на 10 в.; 2 на 2 фізично неможливо.

Набір зразків E

Приклад$\PageIndex{5}$

Дослідження якості повітря в конкретному місті екологічною групою свідчить про те, що$t$ через роки рівень окису вуглецю в частках на мільйон в повітрі буде

$A = 0.3t^2 + 0.1t + 4.2$

а) Який зараз рівень чадного газу в повітрі частинами на мільйон?

Оскільки рівняння$A = 0.3t^2 + 0.1t + 4.2$ визначає рівень$t$ років з цього моменту, ми маємо$t = 0$.

\ (А = 0,3 т ^ 2 + 0,1 т + 4,2\\
А = 4,2\)

б) Через скільки років буде рівень чадного газу на рівні 8 частин на мільйон?

\ (\ begin {масив} {Flushleft}
\ текст {Крок 1:} & t &=\ текст {кількість років, коли рівень} 8\
\ текст {Крок 2:} & 8 &= 0.3t^2 + 0.1t + 4.2\\
\ текст {Крок 3:} & 8 &= 0.3t^2 + 0.1t + 4.2\\ & 0 &= 0.3t^2 + 4.2\\
& 0 &= 0.3t^2 ^ 2+ 0,1 т - 3,8 & \ text {Це не легко фактор, тому ми будемо використовувати квадратичну формулу.}\\
& a &= 0,3, b = 0,1, c = -3.8\\
& t &=\ dfrac {-0.1\ pm\ sqrt {(0,1) ^2 = 4 (0,3)} {2 (0,3)}\\
& &=\ dfrac {-0.1\ pm\ sqrt {0.01 + 4.56}} {0.6} =\ dfrac {-0.1\ pm\ sqrt {4. 57}} {0.6}\\
& &=\ dfrac {-0.1\ pm 2.14} {0,6}\\
& t &= 3.4\ text {і} -3.73
\ end {масив}\) не
$t = -3.73$ має фізичного значення. Перевірити$t = 3.4$

Крок 4: Це значення$t$ округлено до найближчої десятої. Це перевіряє (досить уважно).

Крок 5: Приблизно через 3,4 роки рівень чадного газу буде$8$.

Практика Set E

Завдання практики$\PageIndex{8}$

Дослідження якості повітря в конкретному місті екологічною групою говорить про те, що через t років рівень чадного газу, в частках на мільйон, в повітрі буде

$A = 0.2t^2 + 0.1t + 5.1$

а) Який зараз рівень, частинами на мільйон?

б) Через скільки років буде рівень чадного газу на рівні 8 частин на мільйон? Округлити до найближчої десятої.

Відповідь

(а). 5,1 частин на мільйон

(б). 3,6 років

Набір зразків F

Приклад$\PageIndex{6}$

Підрядник полягає в заливці бетонної доріжки навколо басейну, який 20 футів в ширину і 40 футів в довжину. Площа доріжки повинна бути 544 квадратних футів. Якщо доріжка повинна бути однакової ширини, наскільки широкою повинен її зробити підрядник?

Крок 1: Нехай$x=$ ширина доріжки.

Крок 2: Діаграма допоможе нам отримати рівняння

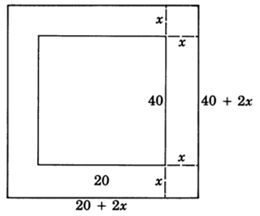
(Площа басейну і доріжки) - (Площа басейну) = (площа доріжки)

$(20 + 2x)(40 + 2x) - 20 \cdot 40 = 544$

\ (\ почати {масив} {Flushleft}
\ текст {Крок 3:} & (20 + 2x) (40 + 2x) - 20\ cdot 40 &= 544\\
& 800 + 120x + 4x^2 - 800 &= 544\\
& 120x + 4x^23 &= 544\\
& 4x^2 + 120x - 544 &= 0 &\ текст {Розділити кожен термін по} 4\\
& x^2+ 30x - 136 &= 0 &\ текст {Вирішити за допомогою факторингу. (або квадратична формула)}\\
& (x-4) (x + 34) &= 0
\ end {масив}\)

\ (\ begin {масив} {Flushleft}
x - 4 &= 0 &\ текст {або} & x + 34 &= 0\\
x &= 4 &\ текст {або} & x &= -34\ текст {не має фізичного значення}
\ end {масив}\)

Перевірте ширину 4 фути як рішення.

\ (\ begin {масив} {Flushleft}
\ текст {Крок 4:} &\ text {Площа басейну та доріжки} &= (20 + 2\ cdot 4) (40 + 2\ cdot 4)\\
& &= (28) (48)\\
& &= 1344
\ end {масив}\)

Площа басейну$=(20)(40) = 800$

Площа доріжки$=1344 - 800 = 544$. Так, це правильно.

Це рішення перевіряє.

Крок 5: Підрядник повинен зробити доріжку шириною 4 фути.

Практика Set F

Завдання практики$\PageIndex{9}$

Підрядник полягає в заливці бетонної доріжки навколо басейну, який 15 футів в ширину і 25 футів в довжину. Площа доріжки повинна бути 276 квадратних футів. Якщо доріжка повинна бути однакової ширини, наскільки широкою повинен її зробити підрядник?

Відповідь

3 фути завширшки

Вправи

Деякі з наведених нижче проблем мають актуальні програми, а деякі призначені лише для розробників логіки. Калькулятор може бути корисним. Проблеми з'являються в групах і відповідають зазначеній задачі Sample Set.

Вибірковий набір проблем типу A

Вправа$\PageIndex{1}$

Виробник електронних паливних форсунок визначає, що$N$ кількість проданих форсунок пов'язано з ціною$x$ за інжектор по$N = 22x - x^2$. За якою ціною виробник повинен цінувати форсунки, щоб 112 з них було продано?

Відповідь

$8 або $14

Вправа$\PageIndex{2}$

Власник вітражного магазину визначає, що$N$ кількість штук того чи іншого виду скла, що продається за місяць, пов'язане з ціною$x$ за штуку по$N = 21x - x^2$. За якою ціною покупець магазину повинен цінувати скло так, щоб 162 продали?

Вправа$\PageIndex{3}$

$t$Підраховано, що через роки населення певного міста буде

$P = t^2 - 15t + 12036$

а) Яке населення зараз?

б) Через скільки років населення становитиме 12 000?

Відповідь

(а) 12 036

(b) 3 і 12 років від тепер

Вправа$\PageIndex{4}$

$t$Підраховано, що через роки населення певного міста буде

$P = t^2 - 16t + 24060$

а) Яке населення зараз?

б) Через скільки років населення становитиме 24 000?

Вправа$\PageIndex{5}$

Якщо об'єкт кидається вертикально вгору, його висота$h$, над землею, в футах, через$t$ секунди$h_0$ задається$h = h_0 + v_0t - 16t^2$, де початкова висота, з якої об'єкт$v_0$ кидається і є початковою швидкістю об'єкта. Використовуючи цю формулу та такий підхід, як у Sample Set A, вирішіть цю задачу.

Куля, кинутий вертикально в повітря, має рівняння руху$h = 48 + 32t - 16t^2$.

а) Наскільки високий м'яч на$t = 0$ (початковій висоті м'яча)?

б) Наскільки високо знаходиться м'яч$t = 1$ (після 1 секунди в повітрі)?

в) Коли м'яч б'є об землю? (Hind: Визначте відповідне значення для$h$ потім вирішити для$t$).

Відповідь

(а) 48 футів

(б) 64 фути

(c)$t = 3$

Вправа$\PageIndex{6}$

Окуляри жінки випадково падають з її обличчя, коли вона дивиться з вікна у високому будинку. Рівняння$h$, що стосується, висота над землею в ногах$t$, і, час в секундах її окуляри падають, є$h = 64 - 16t^2$.

а) Наскільки високо було обличчя жінки, коли її окуляри впали?

б) Через скільки секунд після того, як окуляри впали, вони потрапили в землю?

Вибірковий набір B - Проблеми типу

Вправа$\PageIndex{7}$

Довжина прямокутника на 6 футів більше, ніж удвічі більше ширини. Площа становить 8 квадратних футів. Знайдіть розміри.

Відповідь

довжина = 8; ширина = 1

Вправа$\PageIndex{8}$

Довжина прямокутника на 18 дюймів більше, ніж в три рази більше його ширини. Площа складає 81 квадратний дюйм. Знайдіть розміри.

Вправа$\PageIndex{9}$

Довжина прямокутника становить дві третини його ширини. Площа складає 14 квадратних метрів. Знайдіть розміри.

Відповідь

ширина =$\sqrt{21}$; довжина =$\dfrac{2}{3} \sqrt{21}$

Вправа$\PageIndex{10}$

Довжина прямокутника становить чотири дев'яті його ширини. Площа 144 квадратних футів. Знайдіть розміри.

Вправа$\PageIndex{11}$

Площа трикутника становить 14 квадратних дюймів. Основа на 3 дюйми довша за висоту. Знайдіть як довжину підстави, так і висоту.

Відповідь

$b=7;  h=4$

Вправа$\PageIndex{12}$

Площа трикутника дорівнює 34 квадратним сантиметрам. Підстава на 1 см довше, ніж в два рази більше висоти. Знайдіть як довжину підстави, так і висоту

Зразок набору C - тип задачі

Вправа$\PageIndex{13}$

Добуток двох послідовних цілих чисел дорівнює 72. Знайдіть їх.

Відповідь

−9, −8 або 8,9

Вправа$\PageIndex{14}$

Добуток двох послідовних від'ємних чисел дорівнює 42. Знайдіть їх.

Вправа$\PageIndex{15}$

Добуток двох послідовних непарних цілих чисел дорівнює 143. Знайдіть їх. (Підказка: Квадратне рівняння є факторним, але квадратична формула може бути швидшою.)

Відповідь

−13, −11 або 11,13

Вправа$\PageIndex{16}$

Добуток двох послідовних парних чисел дорівнює 168. Знайдіть їх.

Вправа$\PageIndex{17}$

Три додається до цілого числа і ця сума подвоюється. Коли цей результат множиться на початкове ціле число, добуток дорівнює 20. Знайдіть ціле число.

Відповідь

$n=2,−5$

Вправа$\PageIndex{18}$

Чотири додається до трьох разів цілого числа. Коли цю суму та початкове ціле число множаться, добуток дорівнює −1. Знайдіть ціле число.

Вибірковий набір D - проблеми типу

Вправа$\PageIndex{19}$

Коробка без верху і квадратної основи повинна бути виготовлена шляхом вирізання 2-дюймових квадратів з кожного кута і складання сторін шматка картону. Обсяг коробки повинен бути 25 кубічних дюймів. Якого розміру повинен бути шматок картону?

Відповідь

$4 + \sqrt{12.5}$дюймів

Вправа$\PageIndex{20}$

Коробка без верху і квадратної основи повинна бути виготовлена шляхом вирізання 8-дюймових квадратів з кожного кута і складання сторін шматочка картону. Обсяг коробки повинен бути 124 кубічних дюймів. Якого розміру повинен бути шматок картону?

Вибірковий набір E—Type Проблеми

Вправа$\PageIndex{21}$

Дослідження якості повітря в конкретному місті екологічною групою свідчить про те, що$t$ через роки рівень окису вуглецю в частках на мільйон буде$A = 0.1t^2 + 0.1t + 2.2$.

а) Який зараз рівень чадного газу в повітрі частинами на мільйон?

б) Через скільки років буде рівень чадного газу на рівні 3 частини на мільйон?

Відповідь

(а) окис вуглецю зараз 2,2 частини на мільйон
(б) 2,37 років

Вправа$\PageIndex{22}$

Подібне дослідження з дослідженням проблеми 21 передбачає$A = 0.3t^2 + 0.25t + 3.0$

а) Який зараз рівень чадного газу в повітрі частинами на мільйон?

б) Через скільки років буде рівень чадного газу на рівні 3 частини на мільйон?

Набір зразків F - проблеми типу

Вправа$\PageIndex{23}$

Підрядник полягає в заливці бетонної доріжки навколо болотного басейну, який є 4 футів в ширину і 8 футів в довжину. Площа доріжки та басейну повинна бути 96 квадратних футів. Якщо доріжка повинна бути однакової ширини, наскільки вона повинна бути широкою?

Відповідь

$x=2$

Астрофізична проблема

Вправа$\PageIndex{24}$

Дуже цікавим застосуванням квадратичних рівнянь є визначення довжини сонячного затемнення (Місяця, що проходить між землею і сонцем). Довжину сонячного затемнення знаходять шляхом вирішення квадратного рівняння

$(a + bt)^2 + (c + dt)^2 = (e + ft)^2$

для$t$. Букви$a, b, c, d, e$, і$f$ є константами, які відносяться до певного затемнення. Рівняння являє собою квадратне рівняння в$t$ і може бути вирішене квадратичною формулою (і, безумовно, калькулятором). Два значення результату$t$ волі. Тривалість затемнення якраз і є різницею цих$t$ -значень.

Наступні константи - від сонячного затемнення, яке відбулося 3 серпня 431 року до н.е.

\ (\ почати {масив} {змиває ліворуч}
a &= -619 & b &= 1438\\
c &= 912 & d &= -833\\
e &= 1890.5 & f & = -2
\ кінець {масив}\)

Визначте довжину саме цього сонячного затемнення.

Вправи для огляду

Вправа$\PageIndex{25}$

Знайдіть суму:$\dfrac{2x + 10}{x^2 + x - 2} + \dfrac{x + 3}{x^2 - 3x + 2}$

Відповідь

$\dfrac{3x + 14}{(x+2)(x-2)}$

Вправа$\PageIndex{26}$

Розв'яжіть дробове рівняння$\dfrac{4}{x+12} + \dfrac{3}{x + 3} = \dfrac{4}{x^2 + 5x + 6}$

(Підказка: Перевірте наявність сторонніх рішень)

Вправа$\PageIndex{27}$

Одна труба може заповнити бак за 120 секунд, а інша труба може заповнити той самий бак за 90 секунд. Скільки часу знадобиться обидві труби, що працюють разом, щоб заповнити бак?

Відповідь

$51 \dfrac{3}{7}$

Вправа$\PageIndex{28}$

Використовуйте квадратичну формулу для вирішення$10x^2 - 3x - 1 = 0$

Вправа$\PageIndex{29}$

Використовуйте квадратичну формулу для вирішення$4x^2 - 3x = 0$

Відповідь

$x = 0, \dfrac{3}{4}$