6.5: Факторинг за групуванням
- Page ID
- 58506
Використання групування для множника многочлена
Іноді многочлен не матиме певного фактора, загального для кожного члена. Однак ми все ще можемо створити факторну форму для многочлена.
Поліном не\(x^3+3x^2−6x−18\) має єдиного фактора, який є загальним для кожного члена. Однак ми помічаємо, що якщо ми групуємо разом перші два члени та другі два члени, ми бачимо, що кожен отриманий біноміал має певний фактор, загальний для обох термінів.
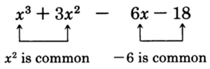
Фактор\(x^2\) з перших двох термінів, і множник\(-6\) з двох двох термінів.
\(x^2(x+3) - 6(x+3)\)
Тепер придивіться до біноміалу. Кожен з двох термінів містить коефіцієнт\(x+3\).
Фактор вихід\((x+3)\).
\((x+3)(x^2-6)\)є остаточною факторизацією
\(x^3+3x^2−6x−18 = (x+3)(x^2-6)\)
Знаючи, коли спробувати метод групування
Нас попереджає ідея групування, коли поліном, який ми розглядаємо, має будь-яку з цих якостей:
- немає фактора, спільного для всіх термінів
- парна кількість термінів
При факторингу шляхом групування знак (\(+\)або\(−\)) фактора, який ми виводимо, зазвичай (але не завжди) буде таким же, як знак першого члена в цій групі.
Набір зразків A
Фактор\(8a^2b^4 - 4b^4 + 14a^2 - 7\)
- Ми помічаємо, що немає фактора, спільного для всіх термінів.
- Ми бачимо, що є чотири терміни, парне число.
- Ми бачимо, що члени 1 і 2 мають\(+4b^4\) спільне (оскільки 1-й член в групі є\(+8a^2b^4\)).
- Зауважимо, що 3-й і 4-й члени мають\(+7\) спільне (так як 1-й член в групі є\(+14a^2\)).
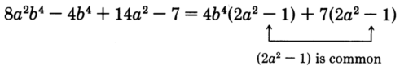
\(8a^2b^4-4b^4+14a^2-7 = (2a^2-1)(4b^4+7)\)
Практика Набір A
Використовуйте метод групування для множника наступних поліномів.
\(ax+ay+bx+by\)
- Відповідь
-
\((a+b) (x+y)\)
\(2am+8m+5an+20n\)
- Відповідь
-
\((2m+5n) (a+4)\)
\(a^2x^3 + 4a^2y^3 + 3bx^3 + 12by^3\)
- Відповідь
-
\((a^2+3b)(x^3 + 4y^3)\)
\(15mx+10nx−6my−4ny\)
- Відповідь
-
\((5x−2y) (3m+2n)\)
\(40abx - 24abxy - 35c^2x + 21c^2xy\)
- Відповідь
-
\(x(8ab−7c^2) (5−3y)\)
При факторингу полінома\(8a^2b^4−4b^4+14a^2−78\) в Sample Set A ми згрупували разом члени 1 і 2 і 3 і 4. Чи могли б ми згрупувати терміни 1 і 3 і 2 і 4? Спробуйте це.
\(8a^2b^4−4b^4+14a^2−78 =\)
- Відповідь
-
Так
Чи отримуємо ми такий же результат? Якщо результати виглядають не точно так само, згадайте комутативну властивість множення.
вправи
Для наступних задач використовуйте метод групування для множників поліномів. Деякі поліноми можуть бути нефакторними за допомогою методу групування.
\(2ab+3a+18b+27\)
- Відповідь
-
\((2b+3)(a+9)\)
\(xy−7x+4y−28\)
\(xy+x+3y+3\)
- Відповідь
-
\((y+1)(x+3)\)
\(mp+3mq+np+3nq\)
\(ar+4as+5br+20bs\)
- Відповідь
-
\((a+5b)(r+4s)\)
\(14ax−6bx+21ay−9by\)
\(12mx−6bx+21ay−9by\)
- Відповідь
-
\(3(4mx−2bx+7ay−3by)\)Не піддається факторингу за групуванням
\(36ak−8ah−27bk+6bh\)
\(a^2b^2 + 2a^2 + 3b^2 + 6\)
- Відповідь
-
\((a^2+3)(b^2+2)\)
\(3n^2 + 6n + 9m^3 + 12m\)
\(8y^4 - 5y^3 + 12z^2 - 10z\)
- Відповідь
-
Не піддається факторингу за групуванням
\(x^2 + 4x - 3y^2 + y\)
\(x^2 - 3x + xy - 3y\)
- Відповідь
-
\((x+y)(x−3)\)
\(2n^2+12n−5mn−30m\)
\(4pq−7p+3q^2−21\)
- Відповідь
-
Не піддається факторингу за групуванням
\(8x^2+16xy−5x−10y\)
\(12s^2−27s−8st+18t\)
- Відповідь
-
\((4s−9)(3s−2t)\)
\(15x^2−12x−10xy+8y\)
\(a^4b^4+3a^5b^5+2a^2b^2+6a^3b^3\)
- Відповідь
-
\(a^2b^2(a^2b^2 + 2)(1 + 3ab)\)
\(4a^3bc−14a^2bc^3+10abc^2−35bc^4\)
\(5x^2y^3z+3x^3yw−10y^3z^2−6wxyz\)
- Відповідь
-
\(y(5y^2z+3xw)(x^2−2z)\)
\(a^3b^2cd+abc^2dx−a^2bxy−cx^2y\)
\(5m^{10}n^{17}p^3 - m^6n^7p^4 - 40m^4n^{10}qt^2 + 8pqt^2\)
- Відповідь
-
\((m^6n^7p^3−8qt^2)(5m^4n^{10}−p)\)
Вправи для рецензування
Спростити\((x^5y^3)(x^2y)\)
Використовуйте наукові позначення, щоб знайти твір\((3 \times 10^{-5})(2 \times 10^2)\).
- Відповідь
-
\(6 \times 10^{-3}\)
Знайти область рівняння\(y = \dfrac{6}{x+5}\)
Побудувати графік нерівності\(y \ge -2\)

- Відповідь
-

Фактор\(8a^4b^4 + 12a^3b^5 - 8a^2b^3\)
