6.4: Найбільший загальний фактор

Метод факторингу

В останніх двох типах проблем ми знали один із факторів і змогли визначити інший фактор через поділ. Припустимо, тепер ми отримали продукт без будь-яких факторів. Наша проблема полягає в тому, щоб знайти фактори, якщо це можливо. Ця процедура і дві попередні процедури засновані на розподільному майні.

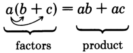
Ми будемо використовувати розподільну властивість в зворотному порядку.

$\underbrace{a b+a c}_{\text {product }}=\underbrace{a(b+c)}_{\text {factors }}$

Ми помічаємо, що в продукті,$a$ є загальним для обох термінів. (Насправді,$a$ є загальним фактором обох термінів.) Оскільки$a$ є спільним для обох термінів, ми будемо враховувати його і написати

$a ()$

Тепер потрібно визначити, що помістити всередині дужок. Це процедура попереднього розділу. Розділіть кожен член твору на відомий фактор$a$.

$\dfrac{ab}{a} = b$і$\dfrac{ac}{a} = c$

Таким чином,$b$ і$c$ є обов'язковими термінами інший фактор. Отже,

$ab + ac = a(b+c)$

При факторингу монома з полінома ми шукаємо фактори, які є не тільки загальними для кожного члена многочлена, але й фактори, які мають ці властивості:

- Чисельні коефіцієнти є найбільшими загальними числовими коефіцієнтами.
- Змінні мають найбільші показники, загальні для всіх змінних.

Найбільший загальний фактор

Мономіальний фактор, який відповідає двом вищезазначеним вимогам, називається найбільшим загальним фактором многочлена.

Набір зразків A

Приклад$\PageIndex{1}$

Фактор$3x - 18$

Найбільшим поширеним фактором є$3$.

\ (\ begin {масив} {Flushleft}
3x-18&=&3\ cdot x - 3\ cdot 6&\ text {Фактор} 3\
3x-18&=&3 () &\ текст {Розділити кожен термін продукту на} 3\\
&&&\ dfrac {3x} {3} = x\ текст {і}\ dfrac {-18} {3} = x\ текст {і}\ dfrac {-18} {3} = -6\\
&&&\ текст {( Спробуйте виконати цей поділ подумки.} \\
3x-18&=&3 (x-6)
\ кінець {масив}\)

Приклад$\PageIndex{2}$

Фактор$9x^3+18x^2+27x$

Зверніть увагу, що$9x$ це найбільший загальний фактор.

$9x^3 + 18x^2 + 27x = 9x \cdot x^2 + 9x \cdot 2x + 9x \cdot 3$. Фактор out$9x$
$9x^3 + 18x^2 + 27x = 9x()$ Подумки$9x$ розділити на кожен термін продукту\)
$9x^3 + 18x^2 + 27x = 9x(x^2+2x+3)$

Приклад$\PageIndex{3}$

Фактор$10x^2y^3 - 20xy^4 - 35y^5$.

Зверніть увагу, що$5y^3$ це найбільший загальний фактор. Фактор вихід$5y^3$.

$10x^2y^3-20xy^4-35y^5 = 5y^3()$

Подумки$5y^3$ розділіть на кожен член твору і помістіть отримані частки всередині ().

$10x^2y^3-20xy^4-35y^5=5y^3(2x^2-4xy-7y^2)$

Приклад$\PageIndex{4}$

Фактор$-12x^5 + 8x^3 - 4x^2$.

Ми бачимо, що найбільшим загальним фактором є$-4x^2$.

$-12x^5 + 8x^3 - 4x^2 = -4x^2()$

Подумки$-4x^2$ розділивши на кожен термін твір, отримуємо

$-12x^5 + 8x^3 - 4x^2 = -4x^2(3x^3 - 2x + 1$

Практика Set A

Завдання практики$\PageIndex{1}$

Фактор$4x−48$.

Відповідь

$4(x−12)$

Завдання практики$\PageIndex{2}$

Фактор$6y^3 + 24y^2 + 36y$

Відповідь

$6y(y^2 + 4y + 6)$

Завдання практики$\PageIndex{3}$

Фактор$10a^5b^4 - 14a^4b^5-8b^6$

Відповідь

$2b^4(5a^5 - 7a^4b - 4b^2$

Завдання практики$\PageIndex{4}$

Фактор$-14m^4 + 28m^2 - 7m$

Відповідь

$-7m(2m^2 - 4m + 1$

Розглянемо цю проблему: фактор$Ax+Ay$. Звичайно,$Ax+Ay=A(x+y)$. Ми знаємо з самого початку нашого вивчення алгебри, що букви представляють одиничні величини. Ми також знаємо, що кількість, що зустрічається в наборі дужок, слід розглядати як єдину величину. Припустимо,$A$ що буква представляє кількість$(a+b)$. Тоді у нас є

$Ax + Ay = A(x+y)$
$(a+b)x + (a+b)y = (a+b)(x+y)$

Коли ми спостерігаємо вираз

$(a+b)x + (a+b)y$

ми помічаємо, що$(a+b)$ є спільним для обох термінів. Оскільки це звичайне явище, ми враховуємо це.

$(a+b)( )$

Як завжди, визначаємо, що помістити всередині дужок, розділивши кожен член твору на$(a+b)$.

$\dfrac{(a+b)x}{(a+b)} = x$і$\dfrac{(a+b)y}{(a+b)} = y$

Це є попередником факторингу, який буде здійснено в розділі 5.4.

Набір зразків B

Приклад$\PageIndex{5}$

Фактор$(x−7)a+(x−7)b$.

Зверніть увагу, що$(x-7)$ це найбільший загальний фактор. Фактор вихід$(x-7)$.

$(x-7)a + (x-7)b = (x-7)( )$
Потім,$\dfrac{(x-7)a}{(x-y)} = a \text{ and } \dfrac{(x-7)b}{(x-7)} = b$
$(x-7)a+(x-7)b = (x-7)(a+b)$

Приклад$\PageIndex{6}$

Фактор$3x^2(x+1)-5x(x+1)$.

Зверніть увагу, що$x$ і$(x+1)$ є загальними для обох термінів. Фактор їх. Ми виконаємо цю факторизацію, дозволяючи$A = x(x+1)$. Тоді у нас є

$3xA-5A = A(3x-5)$
Але$A = x(x+1)$, так
$3x^2(x+1)-5x(x+1) = x(x+1)(3x-5)$

Практика Set B

Завдання практики$\PageIndex{5}$

Фактор$(y+4)a+(y+4)b$.

Відповідь

$(y+4)(a+b)$

Завдання практики$\PageIndex{6}$

Фактор$8m^3(n-4) - 6m^2(n-4)$

Відповідь

$2m^2(n-4)(4m-3)$

Вправи

Для наступних задач множник поліномів.

Вправа$\PageIndex{1}$

$9a+18$

Відповідь

$9(a+2)$

Вправа$\PageIndex{2}$

$6a+24$

Вправа$\PageIndex{3}$

$8b+12$

Відповідь

$4(2b+3)$

Вправа$\PageIndex{4}$

$16x+12$

Вправа$\PageIndex{5}$

$4x−6$

Відповідь

$2(2x−3)$

Вправа$\PageIndex{6}$

$8x−14$

Вправа$\PageIndex{7}$

$21y−28$

Відповідь

$7(3y−4)$

Вправа$\PageIndex{8}$

$16f−36$

Вправа$\PageIndex{9}$

$12x^2 + 18x$

Відповідь

$6x(2x+3)$

Вправа$\PageIndex{10}$

$10y^2 + 15y$

Вправа$\PageIndex{11}$

$8y^2 + 18$

Відповідь

$2(4y^2 + 9)$

Вправа$\PageIndex{12}$

$7x^2 - 21$

Вправа$\PageIndex{13}$

$3y^2 - 6$

Відповідь

$3(y^2 - 2)$

Вправа$\PageIndex{14}$

$2x^2-2$

Вправа$\PageIndex{15}$

$6y^2-6y$

Відповідь

$6y(y−1)$

Вправа$\PageIndex{16}$

$ax^2-a$

Вправа$\PageIndex{17}$

$by^2 + b$

Відповідь

$b(y^2 + 1)$

Вправа$\PageIndex{18}$

$7by^2 + 14b$

Вправа$\PageIndex{19}$

$5a^2x^2 + 10x$

Відповідь

$5x(a^2x + 2)$

Вправа$\PageIndex{20}$

$24ax^2 + 28a$

Вправа$\PageIndex{21}$

$10x^2 + 5x - 15$

Відповідь

$5(2x^2 + x - 3)$

Вправа$\PageIndex{22}$

$12x^2 - 8x - 16$

Вправа$\PageIndex{23}$

$15y^3 - 24y + 9$

Відповідь

$3(5y^3 - 8y + 3)$

Вправа$\PageIndex{24}$

$ax^2 + ax + a$

Вправа$\PageIndex{25}$

$by^3 + by^2 + by + b$

Відповідь

$b(y^3 + y^2 + y + 1)$

Вправа$\PageIndex{26}$

$2y^2 + 6y + 4xy$

Вправа$\PageIndex{27}$

$9x^2 + 6xy + 4x$

Відповідь

$x(9x+6y+4)$

Вправа$\PageIndex{28}$

$30a^2b^2 + 40a^2b^2 + 50a^2b^2$

Вправа$\PageIndex{29}$

$13x^2y^5c - 26x^2y^5c - 39x^2y^5$

Відповідь

$13x^2y^5(-c-3)$

Вправа$\PageIndex{30}$

$-4x^2-12x-8$

Вправа$\PageIndex{31}$

$-6y^3 - 8y^2 - 14y + 10$

Відповідь

$-2(3y^3 + 4y^2 + 7y - 5)$

Вправа$\PageIndex{32}$

$Ab+Ac$

Вправа$\PageIndex{33}$

$Nx+Ny$

Відповідь

$N(x+y)$

Вправа$\PageIndex{34}$

$Qx+Qy$

Вправа$\PageIndex{35}$

$Ax−Ay$

Відповідь

$A(x−y)$

Вправа$\PageIndex{36}$

$(x+4)b+(x+4)c$

Вправа$\PageIndex{37}$

$(x−9)a+(x−9)b$

Відповідь

$(x−9)(a+b)$

Вправа$\PageIndex{38}$

$(2x+7)a+(2x+7)b$

Вправа$\PageIndex{39}$

$(9a−b)w−(9a−b)x$

Відповідь

$(9a−b)(w−x)$

Вправа$\PageIndex{40}$

$(5−v)X+(5−v)Y$

Вправа$\PageIndex{41}$

$3x^5y^4 - 12x^3y^4 + 27x^5y^3 - 6x^2y^6$

Відповідь

$3x^2y^3(x^3y - 4xy + 9x^3-2y^3)$

Вправа$\PageIndex{42}$

$8a^3b^{15} + 24a^2b^{14} + 48a^3b^6 - 20a^3b^7 + 80a^4b^6 - 4a^3b^6 - 4a^3b^7 + 4a^2b$

Вправа$\PageIndex{43}$

$-8x^3y^2 - 3x^3y^2 + 16x^4y^3 + 2x^2y$

Відповідь

$-x^2y(11xy-16x^2y^2-2)$

Вправи для рецензування

Вправа$\PageIndex{44}$

Кількість плюс$21$% більше цієї кількості$26.25$. Яка початкова кількість?

Вправа$\PageIndex{45}$

Вирішити рівняння$6(t−1)=4(5−s)$, якщо$s=2$.

Відповідь

$t=3$

Вправа$\PageIndex{46}$

Враховуючи, що$4a^3$ є фактором$8a^3 - 12a^2$, знайдіть інший фактор.