2.6: Рішення раціональних рівнянь

Last updated
Save as PDF

Page ID: 54552

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Методи розв'язання раціональних рівнянь - це розширення методів, які ви вже знаєте. Нагадаємо, що коли в рівнянні є дроби, ви можете помножити на знаменник, щоб очистити дріб. Ця ж техніка допомагає перетворити раціональні вирази в поліноми, які ви вже вмієте вирішувати. Коли ви множите на константу немає проблем, але коли ви множите через значення, яке змінюється і може бути нульовим, відбуваються цікаві речі.

Оскільки кожне рівняння тривіально вірно, коли обидві сторони множаться на нуль, як ви враховуєте це при вирішенні раціональних рівнянь?

Пошук розв'язків раціональних рівнянь

Першим кроком у вирішенні раціональних рівнянь є перетворення рівняння в поліноміальне рівняння. Це досягається шляхом очищення дробу, що означає множення всього рівняння на загальний знаменник усіх раціональних виразів. Тоді ви повинні вирішити, використовуючи те, що ви вже знаєте. Останнє, що потрібно перевірити, коли у вас є рішення, це те, що вони не роблять знаменники будь-якої частини рівняння рівняння рівним нулю при заміні назад у вихідне рівняння. Якщо так, то це рішення називається стороннім і є «підробленим» рішенням, яке було введено, коли обидві сторони рівняння були помножені на число, яке виявилося нулем.

Візьмемо наступне раціональне рівняння:

\(x-\frac{5}{x+3}=12\)

Щоб знайти розв'язки рівняння, спочатку помножте всі частини рівняння\((x+3),\) на загальний знаменник, а потім спростіть.

\(\begin{aligned} x(x+3)-5 &=12(x+3) \\ x^{2}+3 x-5-12 x-36 &=0 \\ x^{2}-9 x-41 &=0 \\ x &=\frac{-(-9) \pm \sqrt{(-9)^{2}-4 \cdot 1 \cdot(-41)}}{2 \cdot 1} \\ x &=\frac{9 \pm 7 \sqrt{5}}{2} \end{aligned}\)

Єдиним потенційним стороннім рішенням було б -3, оскільки це число, яке робить знаменник вихідного рівняння нулем. Тому можливі обидві відповіді.

Приклади

Приклад 1

Раніше вам було запропоновано врахувати додаткові рішення, введені, коли обидві сторони рівняння множаться на змінну. Для того, щоб розібратися з можливими додатковими рішеннями, ви повинні перевірити кожне рішення, щоб побачити, чи робить він знаменником будь-якого дробу у вихідному рівнянні нуль. Якщо це відбувається, то його називають стороннім розчином.

Приклад 2

Розв'яжіть наступне раціональне рівняння

\(\frac{3 x}{x+4}-\frac{1}{x+2}=-\frac{2}{x^{2}+6 x+8}\)

Помножте кожну частину рівняння на спільний знаменник\(x^{2}+6 x+8=(x+2)(x+4)\)

\(\begin{aligned}(x+2)(x+4)\left[\frac{3 x}{x+4}-\frac{1}{x+2}\right] &=\left[\frac{-2}{(x+2)(x+4)}\right](x+2)(x+4) \\ 3 x(x+2)-(x+4) &=-2 \\ 3 x^{2}+6 x-x-2 &=0 \\ 3 x^{2}+5 x-2 &=0 \\(3 x-1)(x+2) &=0 \\ x &=\frac{1}{3},-2 \end{aligned}\)

Зверніть увагу, що -2 - це стороннє рішення. Єдиним актуальним рішенням є\(x=\frac{1}{3}\).

Приклад 3

Розв'яжіть наступне раціональне рівняння для\(y\).

\(x=2+\frac{1}{2+\frac{1}{y+1}}\)

Це питання можна виконати декількома способами. Ви можете використовувати техніку очищення дробів двічі.

\(\begin{aligned}\left(2+\frac{1}{y+1}\right) x &=\left[2+\frac{1}{2+\frac{1}{y+1}}\right]\left(2+\frac{1}{y+1}\right) \\ 2 x+\frac{x}{y+1} &=2\left(2+\frac{1}{y+1}\right)+1 \\ 2 x+\frac{x}{y+1} &=4+\frac{2}{y+1}+1 \\(y+1)\left[2 x+\frac{x}{y+1}\right] &=\left[5+\frac{2}{y+1}\right](y+1) \\ 2 x(y+1)+x &=5(y+1)+2 \\ 2 x y+2 x+x &=5 y+5+2 \end{aligned}\)

Тепер просто отримати\(y\) змінну на одну сторону рівняння і все інше на іншу сторону.

\(\begin{aligned} 2 x y-5 y &=-3 x+7 \\ y(2 x-5) &=-3 x+7 \\ y &=\frac{-3 x+7}{2 x-5} \end{aligned}\)

Приклад 4

Вирішіть наступне раціональне рівняння.

\(\frac{3 x}{x-5}+4=x\)

\(\begin{aligned} 3 x+4 x-20 &=x^{2}-5 x \\ 0 &=x^{2}-12 x+20 \\ 0 &=(x-2)(x-10) \\ x &=2,10 \end{aligned}\)

Жоден розчин не є стороннім.

Приклад 5

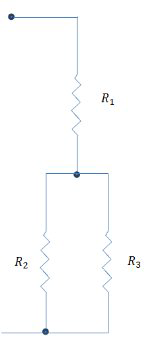
В електричних ланцюгах опір можна вирішити для використання раціональних виразів. Це електрична схема з трьома резисторами. Перший резистор\(R_{1}\) запускається послідовно до двох інших резисторів\(R_{2}\) і\(R_{3}\) які працюють паралельно. Якщо загальний\(R\) опір 100 Ом\(R_{1}\) і і\(R_{3}\) кожен 22 Ом, який опір\(R_{2}\)?

Рівняння значення таке:

\(R=R_{1}+\frac{R_{2} R_{3}}{R_{2}+R_{3}}\)

\(\begin{aligned} 100 &=22+\frac{x \cdot 22}{x+22} \\ 78(x+22) &=22 x \\ 78 x+1716 &=22 x \\ 56 x &=-1716 \\ x &=-30.65 \end{aligned}\)

Подальшим питанням було б запитати, чи можуть Оми бути негативними, що виходить за рамки цього тексту.

Рецензія

Вирішіть наступні раціональні рівняння. Визначте будь-які сторонні рішення.

1. \(\frac{2 x-4}{x}=\frac{16}{x}\)

2. \(\frac{4}{x+1}-\frac{x}{x+1}=2\)

3. \(\frac{5}{x+3}+\frac{2}{x-3}=1\)

4. \(\frac{3}{x-4}-\frac{5}{x+4}=6\)

5. \(\frac{x}{x+1}-\frac{6}{x+2}=4\)

6. \(\frac{x}{x-4}-\frac{4}{x-4}=8\)

7. \(\frac{4 x}{x-2}+3=1\)

8. \(\frac{-2 x}{x+1}+6=-x\)

9. \(\frac{1}{x+2}+1=-2 x\)

10. \(\frac{-6 x-3}{x+1}-3=-4 x\)

11. \(\frac{x+3}{x}-\frac{3}{x+3}=\frac{6}{x^{2}+3 x}\)

12. \(\frac{x-4}{x}-\frac{2}{x-4}=\frac{8}{x^{2}-4 x}\)

13. \(\frac{x+6}{x}-\frac{2}{x+6}=\frac{12}{x^{2}+6 x}\)

14. \(\frac{x+5}{x}-\frac{3}{x+5}=\frac{15}{x^{2}+5 x}\)

15. Поясніть, що означає, щоб рішення було стороннім.