2.5: Поліноміальне довге поділ та синтетичне поділ
- Page ID
- 54529
Хоча ви можете мати досвід в факторингу, завжди будуть поліноми, які не легко фактор, використовуючи основні або передові методи. Як можна визначити коріння цих многочленів?
Раціональні корені та ділильні многочлени
Існують численні теореми, які вказують на взаємозв'язки між поліномами та їх факторами. Наприклад, існує теорема про те, що поліном ступеня\(n\) повинен мати точні\(n\) розв'язки/фактори, які можуть бути дійсними числами, а можуть і не бути. Теорема про раціональний корінь та теорема про залишок - це дві теореми, які є особливо корисними стартовими місцями при маніпулюванні поліномами.
Теорема про раціональний корінь
Теорема про раціональний корінь стверджує, що в поліномі кожен раціональний розв'язок може бути записаний як відновлений дріб,\(\left(x=\frac{p}{q}\right),\) де\(p\) є цілим коефіцієнтом постійного члена і\(q\) є цілим коефіцієнтом провідного коефіцієнта.
Визначимо всі можливі раціональні розв'язки наступного полінома за допомогою теореми Раціонального кореня.
\(12 x^{18}-91 x^{17}+x^{16}+\cdots+2 x^{2}-14 x+5=0\)
Цілочисельні множники 5 дорівнюють 1,5. Цілочисельні множники 12 є 1,2,3,4,6 і\(12 .\) оскільки пари факторів можуть бути негативними, не забудьте включити\(\pm\).
\(\pm \frac{p}{q}=\frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{6}, \frac{1}{12}, \frac{5}{1}, \frac{5}{2}, \frac{5}{3}, \frac{5}{4}, \frac{5}{6}, \frac{5}{12}\)
Можливі рішення можна знайти з цих 24 можливих раціональних відповідей. Якщо це питання вимагало від вас знайти рішення, тоді Теорема про раціональний корінь дасть вам чудове початкове місце. Після того, як у вас є один корінь, ви можете використовувати або поліноміальне довге поділ, або синтетичне, щоб розділити коефіцієнт і продовжувати зменшувати вираз. Ми будемо використовувати теорему про раціональний корінь у прикладі 3.
Поліноміальне довге ділення та теорема про залишок
Поліноміальне довге ділення ідентичне регулярному довгому діленню, за винятком того, що дивіденд і дільник є поліномами замість чисел.
Теорема про залишок стверджує, що залишок полінома,\(f(x)\) поділеного на лінійний дільник,\((x-a)\) дорівнює\(f(a)\). Теорема про залишок корисна лише після того, як ви виконали поліноміальне довге ділення, оскільки вам зазвичай ніколи не дають дільник та залишок для початку. Основною метою теореми про залишок у цій установці є засіб подвійної перевірки вашого застосування поліноміального довгого ділення.
Давайте використаємо ці знання та використаємо поліноміальне довге ділення для поділу:
\(\frac{x^{3}+2 x^{2}-5 x+7}{x-3}\)
По-перше, зауважте, що зрозуміло, що 3 не є коренем многочлена через теорему раціонального кореня, і тому, безумовно, буде залишок. Почніть багаточленне питання з довгим діленням, написавши задачу, подібну до довгої задачі ділення з регулярними числами:
\(- x - 3 \longdiv { x ^ { 3 } + 2 x ^ { 2 } - 5 x + 7 }\)
По-перше, зауважте, що зрозуміло, що 3 не є коренем многочлена через теорему раціонального кореня, і тому, безумовно, буде залишок. Почніть багаточленне питання з довгим діленням, написавши задачу, подібну до довгої задачі ділення з регулярними числами:
\(- x - 3 \longdiv { x ^ { 3 } + 2 x ^ { 2 } - 5 x + 7 }\)
Так само, як і зі звичайними номерами, запитайте себе «скільки\(x\) разів входить\(x^{3}\)?» який в даному випадку є\(x^{2}\).
\(\frac{x^{2}}{x-3) x^{3}+2 x^{2}-5 x+7}\)
Тепер помножте\(x^{2}\) на\(x-3\) і скопіюйте нижче. Не забудьте відняти всю кількість.
\ begin {табличний} {c}
\(x^{2}\)\
\ hline\(x-3) x^{3}+2 x^{2}-5 x+7\)\\
\(-\left(x^{3}-3 x^{2}\right)\)
\ кінець {табличний}
Поєднуємо ряди, збиваємо наступне число і повторюємо.
\(\frac{x^{2}+5 x+10}{3) x^{3}+2 x^{2}-5 x+7}\)
\(\frac{-\left(x^{3}-3 x^{2}\right)}{5 x^{2}-5 x}\)
\(\frac{-\left(5 x^{2}-15 x\right)}{10 x+7}\)
\(\frac{-(10 x-30)}{37}\)
Число 37 - це залишок. На цьому етапі слід подумати про дві речі. По-перше, інтерпретуйте в рівнянні:
\(\frac{x^{3}+2 x^{2}-5 x+7}{x-3}=\left(x^{2}+5 x+10\right)+\frac{37}{x-3}\)
По-друге, перевірте свій результат за допомогою теореми про залишок, яка стверджує, що початкова функція, оцінена на 3, повинна бути 37. Зверніть увагу на позначення, що вказують на заміну 3 в for\(x\).
\(\left.\left(x^{3}+2 x^{2}-5 x+7\right)\right|_{x=3}=3^{3}+2 \cdot 3^{2}-5 \cdot 3+7=27+18-15+7=37\)
Синтетичний поділ
Синтетичне ділення - це скорочений варіант поліноміального довгого ділення, де використовуються тільки коефіцієнти. Синтетичне ділення в основному використовується, коли провідні коефіцієнти чисельника і знаменника рівні 1, а дільник - біном першого ступеня. Давайте використаємо синтетичне ділення, щоб розділити той самий вираз, який ми розділили вище, поліноміальним довгим діленням:
\(\frac{x^{3}+2 x^{2}-5 x+7}{x-3}\)
Замість того, щоб постійно писати і переписувати\(x\) символи, синтетичний поділ спирається на впорядкований інтервал.
\(\pm 3 \mid \begin{array}{llll}1 & 2 & -5 & 7\end{array}\)
Зверніть увагу, як використовуються лише коефіцієнти для знаменника, а дільник включає позитивну трійку, а не негативну трійку. Перший коефіцієнт збивається, а потім множиться на три, щоб отримати значення, яке йде нижче 2.
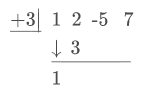
Далі додається новий стовпець. \(2+3=5,\)який йде під\(2^{n d}\) колоною. Тепер, помножити\(5 \cdot+3=15\), який йде під -5 в\(3^{r d}\) стовпці. І процес повторюється...

Останнє число, 37, є залишком. При виписуванні отриманого виразу ви поставите цей залишок над дільником. Три інші числа представляють квадратичне, ідентичне розв'язку результату від ділення виразу за допомогою поліноміального довгого ділення. Зверніть увагу, що при виписуванні виразу ви зменшуєте показник провідного коефіцієнта оригіналу на 1.
\(\left(1 x^{2}+5 x+10\right)+\frac{37}{x-3}\)
Приклади
Раніше вас запитали про визначення коренів поліномів, які не легко чинять фактор, використовуючи методи, які ви вивчили до цього часу. Визначення коренів многочленів вручну може бути складною справою. Найкращий спосіб ідентифікувати корені - використовувати раціональну кореневу теорему для швидкого виявлення ймовірних кандидатів на розв'язки, а потім використовувати синтетичне або поліноміальне довге ділення, щоб швидко та ефективно перевірити їх, щоб перевірити, чи справді їх залишки нульові.
Розділіть наступні многочлени.
\(\frac{x^{3}+2 x^{2}-4 x+8}{x-2}\)
Оскільки провідні коефіцієнти чисельника та знаменника є одночасно 1, а знаменник є біноміальним, синтетичне ділення є хорошим методом для використання тут.
\(\frac{x^{3}+2 x^{2}-4 x+8}{x-2}=x^{2}+4 x+4+\frac{16}{x-2}\)
Повністю множник наступний многочлен.
\(x^{4}+6 x^{3}+3 x^{2}-26 x-24\)
Зверніть увагу, що можливі коріння ± 1,2,3,4,6,8,24. З цих 14 можливостей чотири дадуть залишок нуля. Коли ви знайдете його, використовуйте довгий поділ або синтетичний поділ, щоб визначити корінь, який ви знайшли. Потім знайдіть ще нуль і повторіть процес.
\(x^{4}+6 x^{3}+3 x^{2}-26 x-24\)
\(=(x+1)\left(x^{3}+5 x^{2}-2 x-4\right)\)
\(=(x+1)(x-2)\left(x^{2}+7 x+12\right)\)
\(=(x+1)(x-2)(x+3)(x+4)\)
Перший знайдений нуль був -1. Він був розділений з початкового виразу, щоб знайти залишилася нефакторну частину виразу. Другий знайдений нуль склав 2 від решти шматка і був розділений. Після того, як ви перейдете до квадратичного виразу, ви можете використовувати інші методи факторингу, які ви знаєте, щоб врахувати решту виразу.
Розділіть наступні многочлени.
\(\frac{3 x^{5}-2 x^{2}+10 x-5}{x-1}\)
Оскільки перший коефіцієнт чисельника не дорівнює 1, поліноміальне довге ділення є хорошим методом для використання тут.
\(\frac{3 x^{5}-2 x^{2}+10 x-5}{x-1}=3 x^{4}+3 x^{3}+3 x^{2}+x+11+\frac{6}{x-1}\)
Рецензія
Визначити всі можливі раціональні розв'язки наступних поліномів за допомогою теореми раціонального кореня.
1. \(15 x^{14}-12 x^{13}+x^{12}+\cdots+2 x^{2}-5 x+5=0\)
2. \(18 x^{11}+42 x^{10}+x^{9}+\cdots+x^{2}-3 x+7=0\)
3. \(12 x^{16}+11 x^{15}+3 x^{14}+\cdots+6 x^{2}-2 x+11=0\)
4. \(14 x^{7}-7 x^{6}+x^{5}+\cdots+x^{2}+6 x+3=0\)
5. \(9 x^{9}-10 x^{8}+3 x^{7}+\cdots+4 x^{2}-2 x+2=0\)
Повністю множник наступні многочлени.
6. \(2 x^{4}-x^{3}-21 x^{2}-26 x-8\)
7. \(x^{4}+7 x^{3}+5 x^{2}-31 x-30\)
8. \(x^{4}+3 x^{3}-8 x^{2}-12 x+16\)
9. \(4 x^{4}+19 x^{3}-48 x^{2}-117 x-54\)
10. \(2 x^{4}+17 x^{3}-8 x^{2}-173 x+210\)
Розділіть наступні многочлени.
11. \(\frac{x^{4}+7 x^{3}+5 x^{2}-31 x-30}{x+4}\)
12. \(\frac{x^{4}+7 x^{3}+5 x^{2}-31 x-30}{x+2}\)
13. \(\frac{x^{4}+3 x^{3}-8 x^{2}-12 x+16}{x+3}\)
14. \(\frac{2 x^{4}-x^{3}-21 x^{2}-26 x-8}{x^{3}-x^{2}-10 x-8}\)
15. \(\frac{x^{4}+8 x^{3}+3 x^{2}-32 x-28}{x^{3}+10 x^{2}+23 x+14}\)