3.3: Теорема проміжних значень, існування розв'язку

Last updated
Save as PDF

Page ID: 54367

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Хоча ідея безперервності може здатися дещо базовою, коли функція є безперервною протягом замкнутого інтервалу, як x[ 1,4], ви можете зробити деякі основні висновки. Висновки можуть бути очевидними, коли ви розумієте твердження і дивитеся на графік, але вони, тим не менш, потужні.

Що можна зробити, використовуючи теорему про проміжні значення та теорему екстремальних значень про функцію, яка є неперервною через замкнутий інтервал x[ 1,4]?

Теореми про проміжні та екстремальні значення

Теорема проміжних значень стверджує, що якщо функція є неперервною на замкнутому інтервалі, а u є значенням між f (a) та f (b), то існує c[ a, b] такий, що f (c) =u.

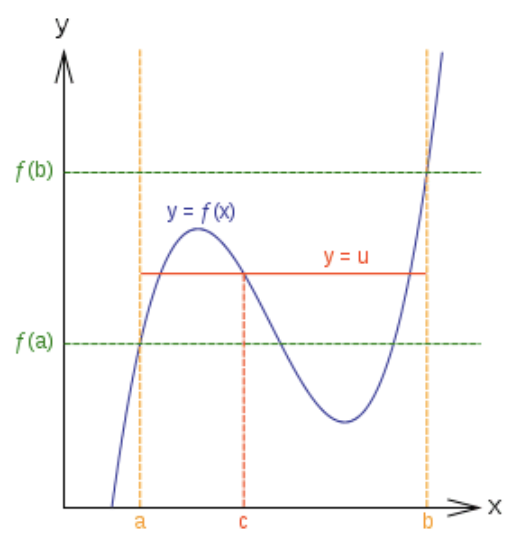
Знімок екрана 2020-09-25 о 11.19.47 AM.png

Фонд СК-12 - http://commons.wikimedia.org/wiki/File:Intermediatevaluetheorem.svg - CC BY-SA

Простіше кажучи, якщо функція є безперервною між низькою та високою точкою, то вона повинна оцінюватися на кожній проміжній висоті між низькою та високою точками.

Зворотне висловлювання if then - це нове твердження з гіпотезою оригінального твердження, переключене з висновком вихідного твердження. Іншими словами, зворотне - це коли якщо частина заяви та тодішня частина заяви міняються місцями. Загалом, зворотне твердження не відповідає дійсності.

Зворотність теореми проміжних значень: Якщо існує значення c[ a, b] таке, що f (c) = u для кожного u між f (a) та f (b), то функція є неперервною.

Це твердження є помилковим. Для того, щоб показати твердження помилково, все, що вам потрібно, це один контрприклад, де кожне проміжне значення потрапляє, а функція розривається.Контрприклад if then твердження - це коли гіпотеза (якщо частина речення) вірна, але висновок (тодішня частина твердження) не відповідає дійсності.

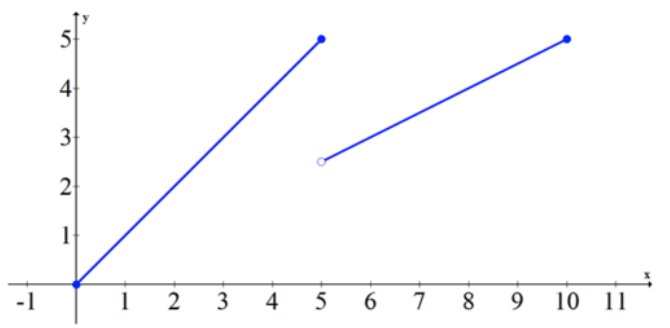
Знімок екрана 2020-09-25 о 11.45.50 AM.png

Фонд CK-12 - CC BY-SA

Ця функція є переривчастою на інтервалі [0,10], але кожне проміжне значення між першою висотою в (0,0) і висотою останньої точки (10,5) потрапляє.

Теорема про екстремальні значення стверджує, що в кожному інтервалі [a, b], де функція є неперервною, існує принаймні один максимум і один мінімум. Іншими словами, вона повинна мати не менше двох крайніх значень.

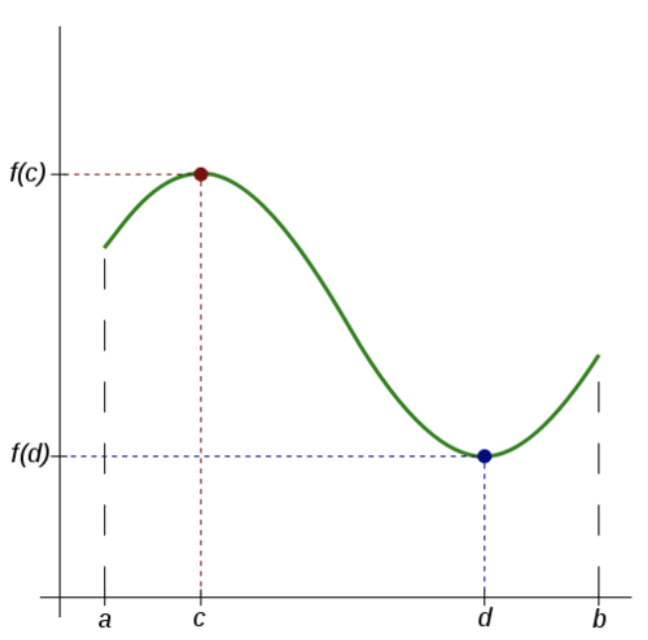
Знімок екрана 2020-09-25 о 11.54.04 AM.png

Фонд СК-12 - http://commons.wikimedia.org/wiki/File:Extreme_Value_Theorem.svg; https://commons.wikimedia.org/wiki/File:CentralParkFromAboveCropped.jpg - CC BY-SA

Зворотність теореми про екстремальні значення : Якщо в замкнутому інтервалі є принаймні один максимум і один мінімум [a, b], то функція є неперервною на [a, b].

Це твердження є помилковим. Для того щоб показати твердження помилкове, все, що вам потрібно, це один контрприклад. Мета полягає в тому, щоб знайти функцію на замкнутому інтервалі [a, b], яка має принаймні один максимум і один мінімум, а також переривчастий.

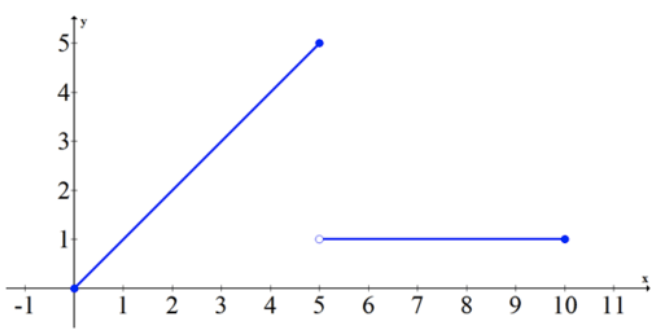
Знімок екрана 2020-09-25 о 11.55.56 AM.png

Фонд CK-12 - CC BY-SA

На інтервалі [0,10] функція досягає максимуму at (5,5) і мінімуму в (0,0), але все ще є переривчастою.

Приклади

Приклад 1

Раніше вам було запропоновано застосувати теореми проміжних та екстремальних значень до функції неперервної на інтервалі xμ [1,4]. За теоремою проміжних значень можна зробити висновок, що існує c[ 1,4] такий, що f (c) = u для кожного u між f (1) та f (4). Також можна зробити висновок, що на цьому інтервалі функція має як максимальне, так і мінімальне значення за теоремою Extreme Value.

Приклад 2

Скористайтеся теоремою проміжних значень, щоб показати, що функція f (x) = (x+1) ³ −4 має нуль на інтервалі [0,3].

Спочатку зауважте, що функція є кубічною і тому є безперервною скрізь.

f (0) = (0+1) ³ −4=1 ³ −4=−3
f (3) = (3+1) ³ −4=4 ³ −4=60

За теоремою проміжних значень має існувати c[ 0,3] такий, що f (c) =0, оскільки 0 знаходиться між -3 та 60.

Приклад 3

Скористайтеся теоремою проміжних значень, щоб показати, що наступне рівняння має принаймні одне дійсне рішення.

х ⁸ = 2 ^х

Спочатку перепишіть рівняння: x8−2x=0

Потім опишіть її як неперервну функцію: f (x) =x8−2x

Ця функція є безперервною, оскільки це різниця двох неперервних функцій.

f (0) =0 ⁸ −2 ⁰ =0−1=−1
f (2) =2 ⁸ −2 ² =256−4=252

За теоремою проміжних значень має існувати c такий, що f (c) =0, оскільки −1<0<252. Число c - один розв'язок початкового рівняння.

Приклад 4

Покажіть, що існує хоча б одне рішення наступного рівняння.

sinx=x+2

Запишіть рівняння як неперервну функцію: f (x) =sinx−x−2

Функція є безперервною, оскільки це сума та різниця неперервних функцій.

f (0) = sin0−0−2=−2
f (−π) = грін (−π) +π−2=0+π−2> 0

За теоремою проміжних значень має існувати c такий, що f (c) =0, оскільки −2<0<π−2. Число c - один розв'язок початкового рівняння.

Приклад 5

Коли вам не дозволяється використовувати теорему про проміжні значення?

Теорема про проміжні значення не повинна застосовуватися, коли функція не є безперервною протягом інтервалу.

Рецензія

Використовуйте теорему проміжних значень, щоб показати, що кожне рівняння має принаймні одне дійсне рішення.

1. cosx=−х

2. лн (х) = е ^−х +1

3. 2х ³ −5х ² = 10х−5

4. х ^3+1=х

5. х ² = кокс

6. х ⁵ = 2х ³ +2

7. 3х ² +4х−11=0

8. 5х ⁴ = 6х ² +1

9. 7х ³ −18х ² −4х+1=0

10. Показати, що f (x) = ^2x−3/ _2x−5 має дійсний корінь на інтервалі [1,2].

11. Показати, що f (x) = ^3x+1/_2x+4 має дійсний корінь на інтервалі [−1,0].

12. True або false: Функція має максимум і мінімум в замкнутому інтервалі [a, b]; отже, функція є безперервною.

13. True або false: Функція є безперервною протягом інтервалу [a, b]; отже, функція має максимум і мінімум в замкнутому інтервалі.

14. True або false: Якщо функція є неперервною протягом інтервалу [a, b], то функція може мати більше одного відносного максимуму в інтервалі [a, b].

15. Яке відношення до теореми проміжного значення та екстремальних значень мають відношення до безперервності?

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 14.7.

Лексика

Термін	Визначення
безперервність	Безперервність для точки існує, коли ліві та праві межі збігаються з функцією, оціненою в цій точці. Щоб функція була неперервною, функція повинна бути неперервною в кожній точці нерозривної області.
Безперервний	Безперервність для точки існує, коли ліві та праві межі збігаються з функцією, оціненою в цій точці. Щоб функція була неперервною, функція повинна бути неперервною в кожній точці нерозривної області.
зворотний	Якщо умовним оператором є p→q (якщо p, то q), то зворотним є q→p (якщо q, то p. Зауважте, що зворотне твердження не відповідає дійсності лише тому, що початковий оператор істинний.
контрприклад	Контрприклад - приклад, який спростовує гіпотезу.
теорема про екстремальне значення	Теорема про крайні значення стверджує, що в кожному інтервалі [a, b], де функція є неперервною, існує принаймні один максимум і один мінімум. Іншими словами, вона повинна мати не менше двох крайніх значень.
теорема проміжного значення	Теорема проміжного значення стверджує, що якщо f (x) є неперервним на деякому інтервалі [a, b], а n знаходиться між f (a) та f (b), то існує деякий c[ a, b] такий, що f (c) = n.

Додаткові ресурси

PLIX: Грайте, вчіться, взаємодійте, досліджуйте - Розвідка функцій

Відео: Правило знаків Декарта - приклад 1

Практика: Теорема проміжних значень, Існування розв'язків

Реальний світ: Злети і падіння