3.4: Знайдіть уявні рішення

Луї обчислює, що площа прямокутника представлена рівнянням 3х ⁴ + 7х ² = 2. Чи правильно це розрахував Луї? Поясніть на основі ступеня і нулів функції.

---

уявні рішення

Пам'ятайте, уявні рішення завжди приходять парами. Щоб знайти уявні розв'язки функції, скористайтеся квадратичною формулою.

Давайте розв'яжемо f (x) =3x ⁴ −x ² −14.

По-перше, ця квартична функція може бути врахована так само, як квадратне рівняння.

г (х) = х ⁴ +21х ² +90

Тепер, оскільки жоден фактор не може бути врахований далі і немає x−term, ми можемо встановити кожен рівний нулю і вирішити.

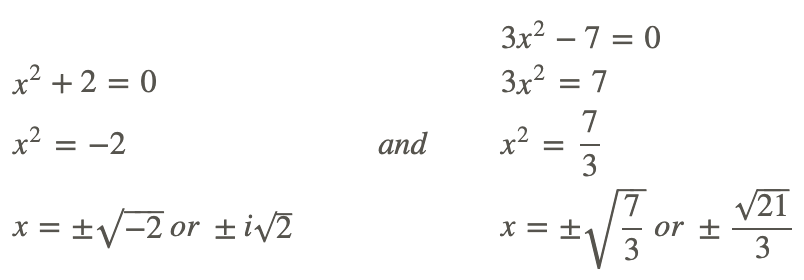
Включаючи уявні рішення, є чотири, що ми очікуємо, оскільки ступінь цієї функції чотири.

Тепер знайдемо всі розв'язки функції g (x) =x ⁴ +21x ² +90.

Якщо позначено графіки, ця функція не торкається осі x. Тому всі рішення є уявними. Для вирішення ця функція може бути врахована як квадратне рівняння. Фактори 90, які складають до 21, - це 6 і 15.

г (х) 0=х ⁴ +21х ² +9

0= (х ² +6) (х ² +15)

Тепер встановіть кожен коефіцієнт рівним нулю і вирішуйте.

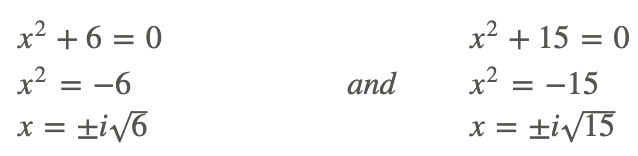
Нарешті, давайте знайдемо функцію, яка має рішення 3, -2 і 4+i.

Зверніть увагу, що одне з заданих рішень передбачає уявне число. Уявні та складні розв'язки завжди попарно, тому 4−i також є фактором. Два фактори - це складні кон'югати. Переведіть кожне рішення в коефіцієнт і помножте їх все разом.

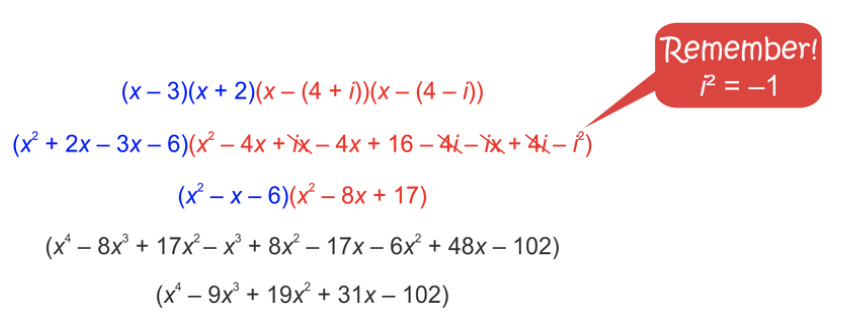
Бахман Калантарі - https://commons.wikimedia.org/wiki/File%3ANonfractal_polynomiograph.png

Будь-яка кратна ця функція також матиме ці корені. Наприклад, 2x4−18x3+38x2+62x−204 також матиме ці корені.

---

Приклади

Приклад 1

Раніше вас попросили визначити, чи правильно розрахував Людовик свою роботу.

Для початку нам потрібно змінити рівняння на стандартну форму. Тоді ми можемо це врахувати.

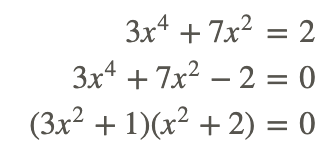
Рішення для х отримуємо

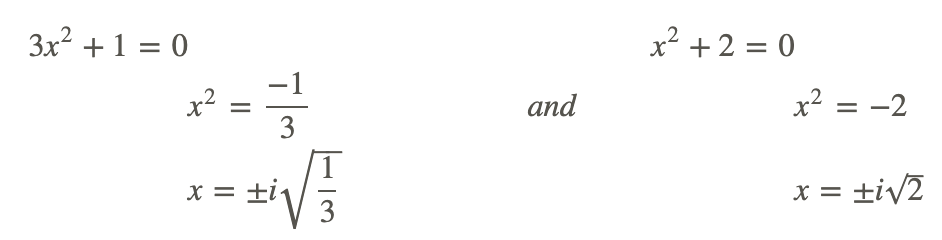
Всі рішення є уявними, і площа прямокутника повинна мати реальні рішення. Тому Людовик не розрахував правильно.

Приклад 2

Знайти всі розв'язки такої функції: f (x) =25x3−120x2+81x−4.

Спочатку наведіть графік функції.

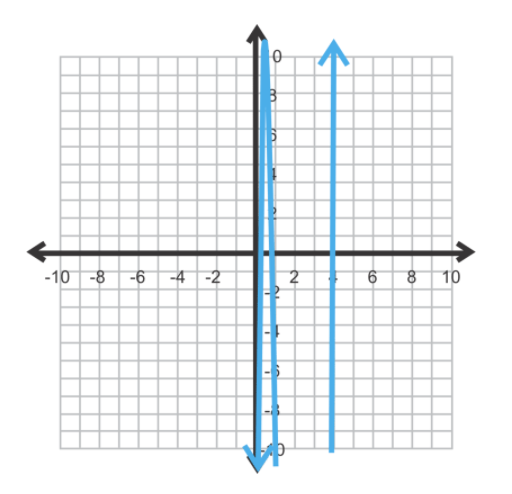
^{Використовуючи теорему раціонального кореня, можливі реалістичні нулі можуть бути _1/25, 1 або 4.} Спробуємо ці три можливості за допомогою синтетичного поділу.

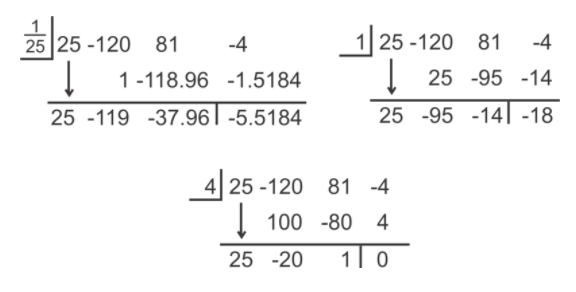
З цих трьох можливостей тільки 4 - це нуль. Залишковий многочлен, 25x ² −20x+1, не є факторним, тому нам потрібно скористатися Квадратичною формулою, щоб знайти останні два нулі.

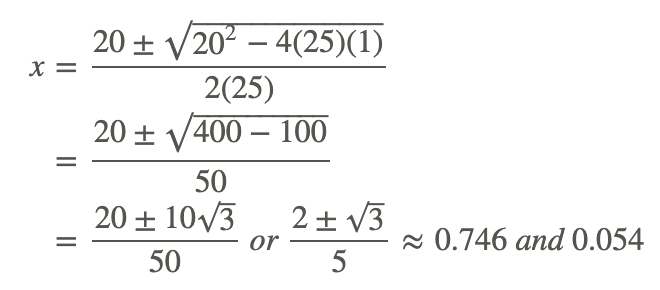
Корисна підказка: Завжди знаходьте десяткові значення кожного нуля, щоб переконатися, що вони збігаються з графіком.

Приклад 3

Знайти всі розв'язки такої функції: f (x) =4x ⁴ +35x ² −9.

f (x) = 4x ⁴ +35x ² −9 є факторним. ac=−36.

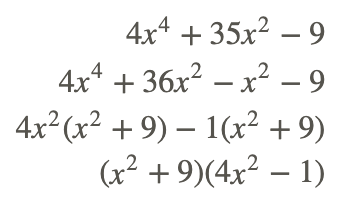
Встановлюючи кожен коефіцієнт рівним нулю, ми маємо:

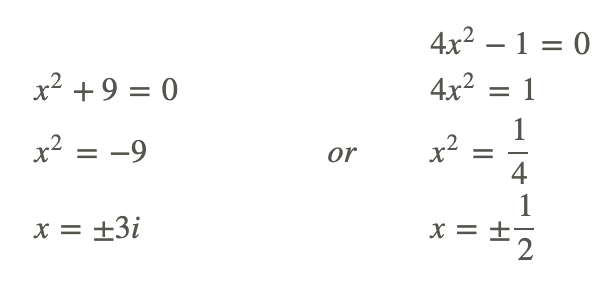
Приклад 4

Знайти рівняння функції з коренями 4, 2, ^0,5 та 1−i.

Нагадаємо, що ірраціональні і уявні коріння йдуть парами. Отже, всі корені 4, 2 ^0,5, −2 ^0,5, 1+i,1−i.

---

Рецензія

Знайдіть всі рішення для наступних функцій. Використовуйте будь-який метод.

1. f (x) = х ⁴ +х ³ −12х ² −10х+20
2. f (x) = 4х ³ −20х ² −3х+15
3. f (x) = 2х ⁴ −7х ² −30
4. ф (х) = х ³ +5х ² +12х+18
5. ф (х) = 4х ⁴ +4х ³ −22х ² −8х+40
6. ф (х) = 3х ⁴ +4х ² −15
7. f (x) = 2х ³ −6х ² +9х−27
8. f (x) = 6x ⁴ −7x ³ −280x ² −419х+280
9. ф (х) = 9х ⁴ +6х ³ −28х ² +2х+11
10. ф (х) = 2х ⁵ −19х ⁴ +30х ³ +97х ² −20х+150

Знайдіть функцію з наступними коренями.

11. 4, я
12. −3, −2i
13. 5 ^0,5, −1+i
14. 2,13,4−2 ^0,5
15. Запис: Запишіть кроки, які ви використовуєте, щоб знайти всі нулі поліноміальної функції.
16. Писання: Чому уявні та ірраціональні коріння завжди приходять парами?
17. Завдання: Знайти всі рішення для f (x) =x5+x3+8x2+8.

---

Відповіді на проблеми з оглядом

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 6.12.

---

Лексика

Термін	Визначення
Складний кон'югат	Складні кон'югати - це пари складних біноміалів. Складний кон'югат a+bi є a−bi. При множенні складних сполучень виходить єдине дійсне число.
комплексне число	Комплексне число - це сума дійсного числа і уявного числа, записаного у вигляді a+bi.
теорема сполучених пар	Теорема спряжених пар стверджує, що якщо f (z) є поліномом ступеня n, з n0 і з дійсними коефіцієнтами, а якщо f (z0) =0, де z0=a+bi, то f (z∗ 0) =0. Де z∗ 0 - складний кон'югат z0.
фундаментальна теорема алгебри	Фундаментальна теорема алгебри стверджує, що якщо f (x) є поліномом ступеня n≥1, то f (x) має принаймні один нуль у комплексній числовій області. Іншими словами, існує хоча б одне комплексне число c таке, що f (c) =0. Теорему можна також викласти так: поліном n-го ступеня з дійсними або комплексними коефіцієнтами має, з кратністю, рівно n комплексних коренів.
Уявне число	Уявне число - це число, яке можна записати як добуток дійсного числа і i.
уявні числа	Уявне число - це число, яке можна записати як добуток дійсного числа і i.
многочлен	Многочлен - це вираз з принаймні одним алгебраїчним терміном, але який не вказує на поділ на змінну або містить змінні з дробовими показниками.
Коріння	Коріння функції - це значення x, які роблять y рівним нулю.
Нульовий	Нулі функції f (x) - це значення x, які змушують f (x) дорівнювати нулю.
нулі	Нулі функції f (x) - це значення x, які призводять до того, що f (x) дорівнює нулю.

---

Додаткові ресурси

PLIX: Грайте, вчіться, взаємодійте, досліджуйте - уявні нулі

Відео: Фундаментальна теорема алгебри - огляд

Практика: Знайдіть уявні рішення