Skip to main content
LibreTexts - Ukrayinska

1.6: Властивості ліміту

  1. Last updated
  2. Save as PDF
  • Page ID
    54364

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Ви знайомі з ідеєю обмеження функції, і що деякі межі обчислюються за допомогою числових і графічних методів. Ліміти також можуть бути оцінені за допомогою властивостей лімітів. Як би ти знайшов

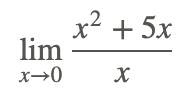
    Знімок екрана 2020-08-24 о 8.30.38 AM.png

    без використання графіка або використання таблиці значень?

    Властивості лімітів

    Почнемо з деяких спостережень про межі деяких простих функцій. Розглянемо наступні граничні проблеми:

    Знімок екрана 2020-08-24 о 8.31.42 AM.png

    Відзначимо, що кожна з цих функцій визначена для всіх дійсних чисел. Якщо ми застосуємо свою інтуїцію для пошуку меж, ми правильно робимо висновок, що:

    Знімок екрана 2020-08-24 о 8.33.13 AM.png

    Наведені вище результати можуть бути інкапсульовані в таких граничних властивостях:

    Основні граничні властивості:

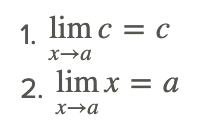
    Знімок екрана 2020-08-24 о 8.33.44 AM.png

    Багато функцій можуть бути виражені у вигляді сум, відмінностей, добутків, коефіцієнтів, повноважень і коренів інших більш простих функцій. Наступні властивості також корисні при оцінці лімітів:

    Додаткові основні граничні властивості:

    Знімок екрана 2020-08-24 о 8.34.25 AM.png

    Знаючи ці властивості, дозволяє оцінити межі широкого спектру функцій.

    Візьмемо проблему:

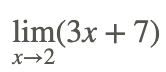
    Знімок екрана 2020-08-24 о 8.37.33 AM.png

    Виходячи з вищезазначених властивостей, межа може бути оцінена в наступних кроках:

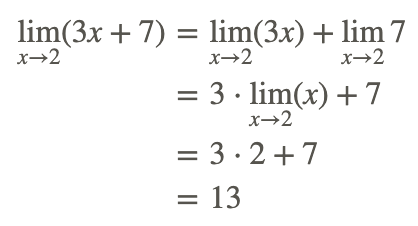
    Знімок екрана 2020-08-24 о 8.38.01 AM.png

    Тому:

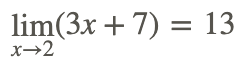
    Знімок екрана 2020-08-24 о 8.38.33 AM.png

    Зауважте, що застосування базових граничних властивостей призводить, в даному випадку, до граничного значення, яке таке ж, як пряма заміна x=2 у функції.

    Тепер оцініть

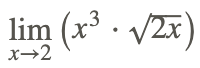
    Знімок екрана 2020-08-24 о 8.42.03 AM.png

    Виходячи з властивостей лімітів, ліміт можна оцінити за наступними кроками:

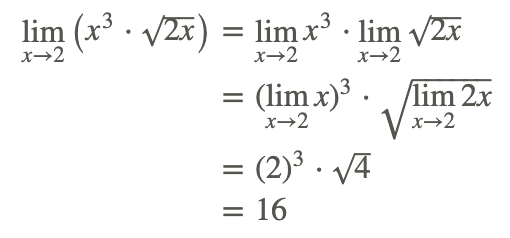
    Знімок екрана 2020-08-24 о 8.42.56 AM.png

    Тому:

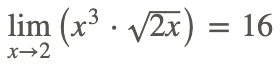
    Знімок екрана 2020-08-24 о 8.43.31 AM.png

    Знову ж таки, зауважте, що застосування основних граничних властивостей призводить, в даному випадку, до граничного значення, яке таке ж, як пряма заміна x=2 у функції.

    Приклади

    Приклад 1

    Раніше вас просили знайти

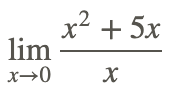
    Знімок екрана 2020-08-24 о 8.44.20 AM.png

    без використання графіка або таблиці значень. Це випадок, коли пряма заміна для оцінки межі дає невизначену форму 0/0. Але, зменшивши дріб і потім застосувавши основні граничні властивості вище, ми можемо оцінити ліміт:

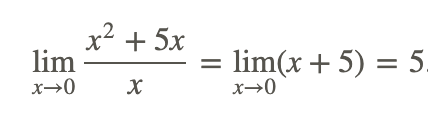
    Знімок екрана 2020-08-24 о 8.44.52 AM.png

    Приклад 2

    Оцінити

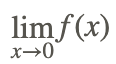
    Знімок екрана 2020-08-24 в 9.40.37 AM.png

    де f (x) - раціональна функція

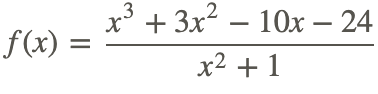
    Знімок екрана 2020-08-24 в 9.46.41 AM.png

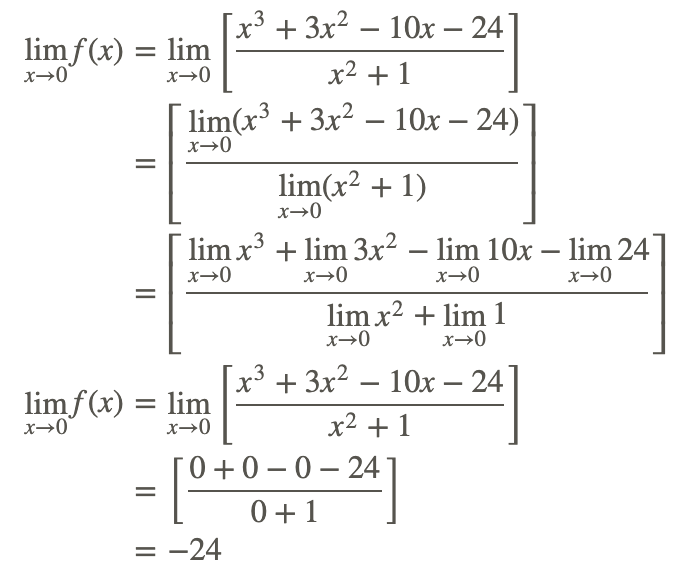
    Знімок екрана 2020-08-31 о 10.30.41 AM.png

    Приклад 3

    Знайдіть наступний ліміт, якщо він існує:

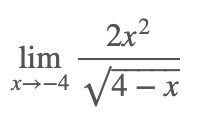
    Знімок екрана 2020-08-31 о 11.07.43 AM.png

    Давайте застосуємо основне правило частки, щоб оцінити цю межу.

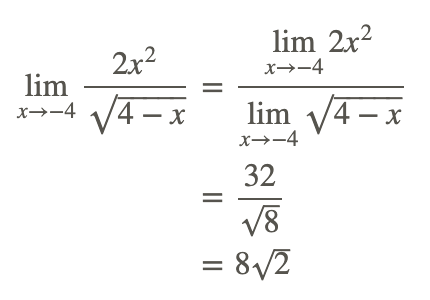
    Знімок екрана 2020-08-31 о 11.19.55 AM.png

    Тому:

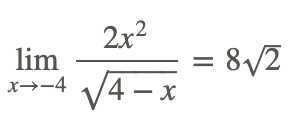
    Знімок екрана 2020-08-31 о 11.32.39 AM.png

    Знову ж таки, результат ліміту збігається з використанням прямої підміни x = −4 у функції.

    Рецензія

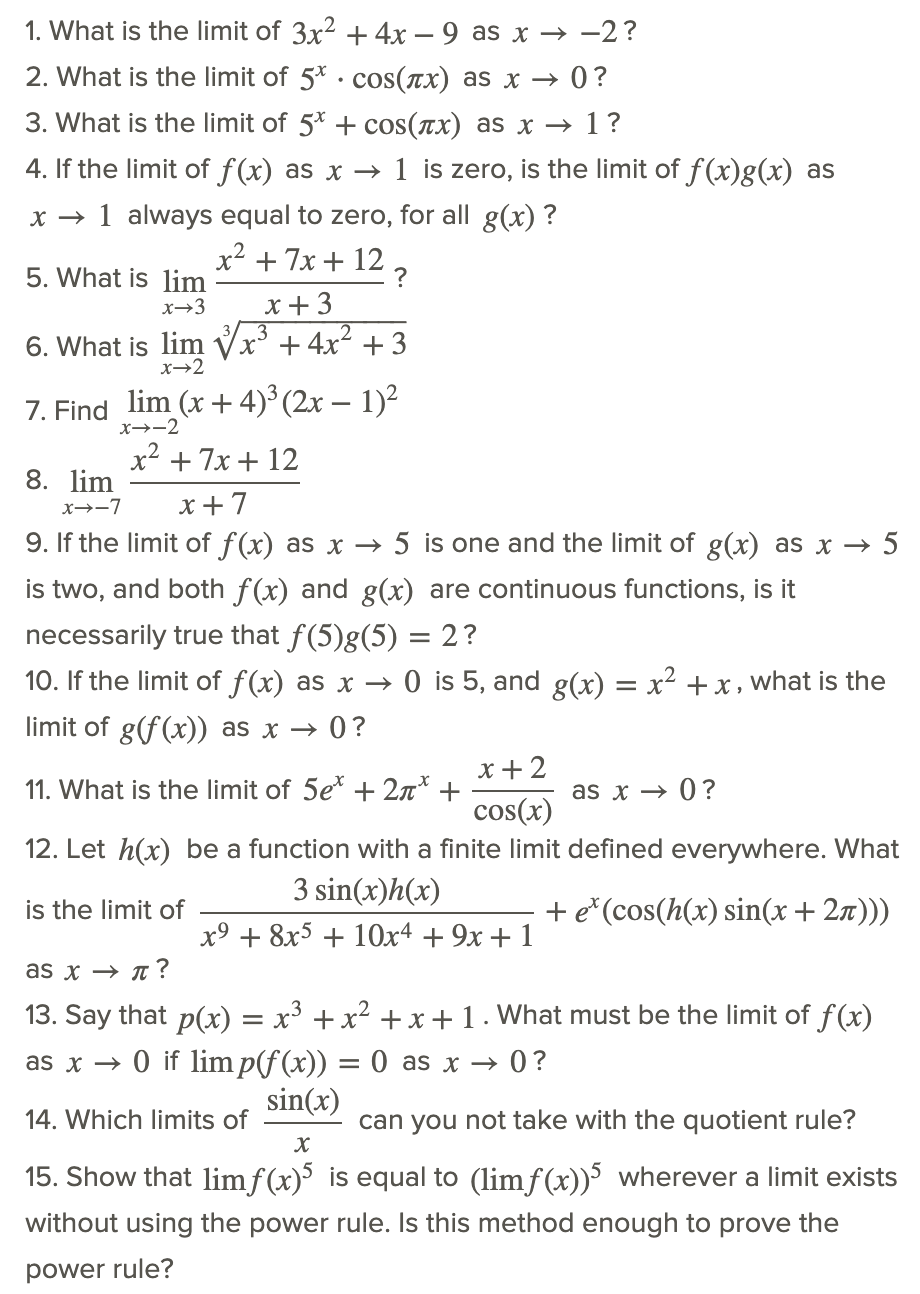
    Знімок екрана 2020-08-31 о 11.33.07 AM.png

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 2.3.

    Лексика

    Термін Визначення
    невизначені У математиці вираз є невизначеною, якщо вона точно не визначена. Існує сім невизначених форм: 0/0, 0⋅∞, ∞, ∞, 0, ∞ 0 та 1 ∞.
    межа Межа - це значення, до якого наближається вихід функції, коли вхід функції наближається до заданого значення.

    Додаткові ресурси

    Практика: Властивості меж