9.22: Площа поверхні та об'єм конусів
- Page ID
- 54436
Площа поверхні дорівнює площі кола плюс площа зовнішньої сторони конуса
Шишки
Конус являє собою тверду речовину з круглою основою і сторонами, які звужуються до вершини. Конус утворюється з обертання прямокутного трикутника, навколо однієї ноги. Конус має похилу висоту.

Площа поверхні
Площа поверхні - це двовимірне вимірювання, яке є загальною площею всіх поверхонь, які зв'язали тверде тіло. Основною одиницею площі є квадратна одиниця. Для площі поверхні конуса нам знадобиться сума площі підстави і площі сторін.
Площа поверхні правого конуса:\(SA= \pi r^{2}+ \pi rl\).

Площа підстави:\(\pi r^{2}\)
Площа сторін:\(\pi rl\)
Обсяг
Щоб знайти обсяг будь-якого твердого тіла, ви повинні з'ясувати, скільки місця воно займає. Основною одиницею об'єму є кубічна одиниця.
Об'єм конуса:\(V=\dfrac{1}{3} \pi r^{2} h\).

Що робити, якщо вам дали тривимірну тверду фігуру з круговою основою та сторонами, які звужуються до вершини? Як ви могли визначити, скільки двовимірного та тривимірного простору займає ця фігура?
Приклад\(\PageIndex{1}\)
Площа поверхні конуса становить,\(36 \pi\) а радіус - 4 одиниці. Що таке похила висота?
Рішення
Підключіть те, що ви знаєте, до формули площі поверхні конуса і вирішіть для\(l\).
\(\begin{aligned} 36 \pi&= \pi 4^{2}+ \pi 4l \\ 36&=16+4l \qquad \text{ When each term has a } \pi \text{, they cancel out.} \\ 20&=4l \\ 5&=l\end{aligned}\)
Приклад\(\PageIndex{2}\)
Обсяг конуса дорівнює,\(484 \pi \text{ cm}^{3}\) а висота - 12 см. Що таке радіус?

Рішення
Підключіть те, що ви знаєте, до формули гучності.
\(\begin{aligned} 484 \pi&=\dfrac{1}{3} \pi r^{2}(12) \\ 121&=r^{2} \\ 11 \text{ cm}&=r\end{aligned}\)
Приклад\(\PageIndex{3}\)
Яка площа поверхні конуса?

Рішення
Для початку нам потрібно знайти висоту нахилу. Використовуйте теорему Піфагора.
\(\begin{aligned} l^{2}&=9^{2}+21^{2} \\ &=81+441 \\ l&=\sqrt{522}\cong 22.85\end{aligned]\)
Загальна площа поверхні, значить, дорівнює\(SA= \pi 9^{2}+ \pi(9)(22.85)\cong 900.54 \text{ units}^{2}\).
Приклад\(\PageIndex{4}\)
Знайдіть обсяг конуса.

Рішення
По-перше, нам потрібна висота. Використовуйте теорему Піфагора.
\(\begin{aligned} 5^{2}+h^{2}&=15^{2} \\ h&=\sqrt{200}=10\sqrt{2} \\ V&=13(5^{2})(10\sqrt{2}) \pi \cong 370.24 \text{ units}^{3}\end{aligned}\)
Приклад\(\PageIndex{5}\)
Знайдіть обсяг конуса.
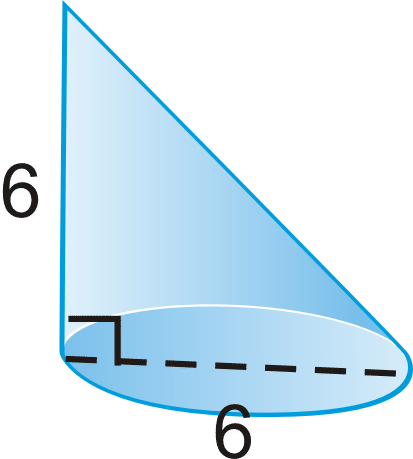
Рішення
Ми можемо використовувати ту ж формулу обсягу. Знайдіть радіус.
\(V=\dfrac{1}{3} \pi(3^{2})(6)=18 \pi \cong 56.55 \text{ units}^{3}\)
Рецензія
Використовуйте конус для заповнення заготовок.

- v є ___________.
- Висота конуса - ______.
- х є __________ і це ___________ конуса.
- w є _____________ ____________.
Намалюйте наступний суцільний і дайте відповідь на питання. Ваш малюнок повинен бути в масштабі, але не один-на-один. Залиште свою відповідь в найпростішій радикальній формі.
- Намалюйте правильний конус радіусом 5 см і висотою 15 см. Що таке похила висота?
Знайдіть висоту нахилу однієї бічної грані в конусі.\(l\) Округлите свою відповідь до найближчої сотої.
-

Малюнок\(\PageIndex{9}\)
Знайдіть площу поверхні і обсяг правильних конусів. Округляйте відповіді до 2 знаків після коми.
-

Малюнок\(\PageIndex{10}\) -

Малюнок\(\PageIndex{11}\) - Якщо площа бічної поверхні конуса дорівнює,\(30 \pi \text{ cm}^{2}\) а радіус 5 см, яка висота нахилу?
- Якщо площа поверхні конуса дорівнює,\(105 \pi \text{ cm}^{2}\) а висота нахилу становить 8 см, який радіус?
- Якщо обсяг конуса дорівнює\( 30 \pi \text{ cm}^{3}\) і радіус 5 см, яка висота?
- Якщо обсяг конуса дорівнює\(105 \pi \text{ cm}^{3}\) і висота 35 см, який радіус?
Огляд (Відповіді)
Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 11.6.
Лексика
| Термін | Визначення |
|---|---|
| конус | являє собою тверду речовину з круглою основою і сторонами, які звужуються до вершини. Конус має похилу висоту. |
| Висота нахилу | Висота нахилу - це висота бічної грані піраміди. |
Додаткові ресурси
Інтерактивний елемент
Відео: Площа поверхні конуса - огляд
Види діяльності: Конуси Питання обговорення
Навчальні посібники: Піраміди та конуси
Практика: Площа поверхні та об'єм конусів