9.18: Площа поверхні та об'єм циліндрів
- Page ID
- 54465
Площа поверхні та об'єм твердих тіл з конгруентними круговими основами в паралельних площинях.
Циліндри
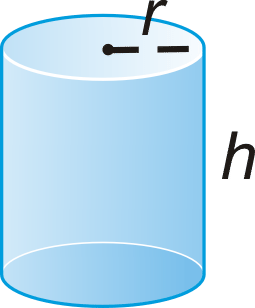
Циліндр - це тверда речовина з конгруентними круговими основами, які знаходяться в паралельних площинам. Простір між колами укладається.
Циліндр має радіус і висоту .

Циліндр також може бути косим (похилим), як і нижче.

Площа поверхні
Площа поверхні - це сума площі граней твердого тіла. Основною одиницею площі є квадратна одиниця.
Площа поверхні правого циліндра:\(SA=2 \pi r^{2}+2 \pi r h\).

\(\underbrace{2 \pi r^{2}}_\text{area of both circles}+ \underbrace{2 \pi r h}_\text{length of rectangle}\)
Обсяг
Щоб знайти обсяг будь-якого твердого тіла, ви повинні з'ясувати, скільки місця воно займає. Основною одиницею об'єму є кубічна одиниця. Для циліндрів обсяг - це площа круглої основи, що помножена на висоту.
Обсяг циліндра:\(V= \pi r^{2}h\)
Якщо косий циліндр має таку ж площу підстави і висоту, що і інший циліндр, то він буде мати такий же обсяг. Це пов'язано з принципом Кавальєрі, який стверджує, що якщо два твердих тіла мають однакову висоту і однакову площу поперечного перерізу на кожному рівні, то вони матимуть однаковий обсяг.
Що робити, якщо вам дали суцільну тривимірну фігуру з конгруентними укладеними круговими основами, які знаходяться в паралельних площинам? Як ви могли визначити, скільки двовимірного та тривимірного простору займає ця фігура?
Приклад\(\PageIndex{1}\)
Якщо об'єм циліндра дорівнює,\(484 \pi in^{3}\) а висота дорівнює 4 дюйма, який радіус?
Рішення
Вирішити для\(r\).
\(\begin{aligned} 484 \pi&= \pi r^{2}(4) \\ 121&=r^{2} \\ 11\text{ in}&=r\end{aligned}\)
Приклад\(\PageIndex{2}\)
Окружність підстави циліндра -\(80 \pi\) см, а висота - 36 см. Знайдіть загальну площу поверхні.
Рішення
Нам потрібно вирішити для радіуса, використовуючи окружність.
\(\begin{aligned} 2 \pi r&=80 \pi \\ r&=40\end{aligned}\)
Тепер ми можемо знайти площу поверхні.
\(\begin{aligned} SA&=2 \pi(40)^{2}+(80 \pi)(36) \\ &=3200 \pi+2880 \pi \\ &=6080 \pi \text{ units}^{2}\end{aligned}\)
Приклад\(\PageIndex{3}\)
Знайдіть площу поверхні циліндра.

Рішення
\(r=4\)і\(h=12\).
\(\begin{aligned} SA&=2 \pi(4)^{2}+2 \pi(4)(12) \\ &=32 \pi+96 \pi \\ &=128 \pi \text{ units}^{2}\end{aligned} \)
Приклад\(\PageIndex{4}\)
Окружність основи циліндра дорівнює,\(16 \pi\) а висота дорівнює 21. Знайдіть площу поверхні циліндра.
Рішення
Нам потрібно вирішити для радіуса, використовуючи окружність.
\(\begin{aligned} 2 \pi r&=16 \pi \\ r&=8\end{aligned}\)
Тепер ми можемо знайти площу поверхні.
\(\begin{aligned} SA&=2 \pi(8)2+(16 \pi)(21) \\ &=128 \pi+336 \pi \\ &=464 \pi \text{ units}^{2}\end{aligned}\)
Приклад\(\PageIndex{5}\)
Знайдіть обсяг циліндра.

Рішення
Якщо діаметр дорівнює 16, то радіус дорівнює 8.
\(\begin{aligned} V&= \pi 8^{2}(21) \\ &=1344 \pi \text{ units}^{3}\end{aligned}\)
Рецензія
- Два циліндра мають однакову площу поверхні. Чи мають вони однаковий обсяг? Звідки ти знаєш?
- Циліндр має\(r=h\) і радіус дорівнює 4 см. Що таке обсяг?
- Циліндр має обсяг\(486 \pi \text{ ft}^{3}\). Якщо висота 6 футів, який діаметр?
- Правий циліндр має радіус 7 см і висоту 18 см. Знайдіть обсяг.
Знайдіть обсяг наступних твердих тіл. Округляйте свої відповіді до найближчих сотих.
-

Малюнок\(\PageIndex{7}\) -

Малюнок\(\PageIndex{8}\)
Знайдіть значення x, задане об'ємом.
- \(V=6144 \pi \text{ units}^{3}\)

Малюнок\(\PageIndex{9}\) - Площа підстави циліндра становить,\(49 \pi \text{ in}^{2}\) а висота - 6 дюймів. Знайдіть обсяг.
- Окружність підстави циліндра дорівнює\(34 \pi \text{ cm}\) і висота - 20 см. Знайдіть загальну площу поверхні.
- Площа бічної поверхні циліндра дорівнює,\(30 \pi \text{ m}^{2}\) а висота 5 м Який радіус?
Огляд (Відповіді)
Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 11.4.
Лексика
| Термін | Визначення |
|---|---|
| циліндр | Тверда речовина з конгруентними круговими основами, які знаходяться в паралельних площинам. Простір між колами укладається. Циліндр має радіус і висоту, а також може бути косим (похилим). |
| Площа поверхні | Площа поверхні - це загальна площа всіх поверхонь тривимірного об'єкта. |
| Обсяг | Об'єм - це кількість простору всередині меж тривимірного об'єкта. |
| Принцип Кавальєрі | Заявляється, що якщо два твердих тіла мають однакову висоту і однакову площу поперечного перерізу на кожному рівні, то вони будуть мати однаковий обсяг. |
| Косий циліндр | Косий циліндр - це циліндр з підставами, які не знаходяться безпосередньо один над одним. |
Додаткові ресурси
Інтерактивний елемент
Відео: Принципи циліндрів - основні
Діяльність: Циліндри Обговорення Питання
Навчальні посібники: посібник з вивчення призм та циліндрів
Практика: Площа поверхні та об'єм циліндрів
Реальний світ: Бурові команди