1.9: Вимірювання кутів

Last updated
Save as PDF

Page ID: 54993

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Вимірювання кутів за допомогою транспортирів та постулат додавання кута.

Кути

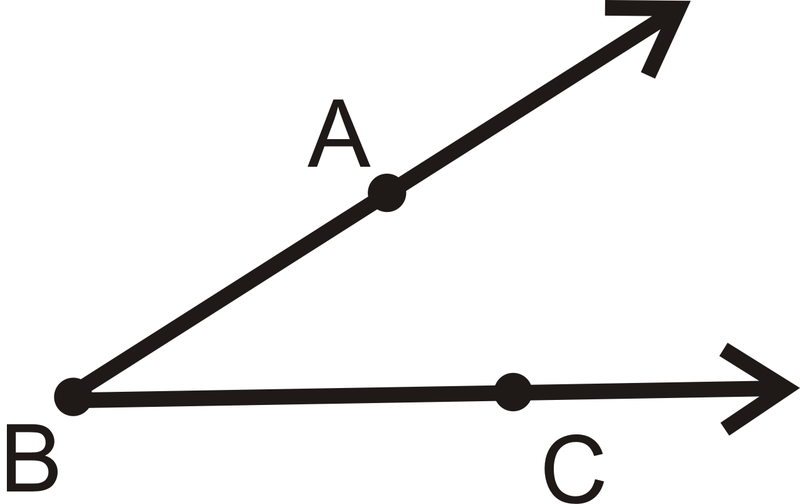
Кут утворюється, коли два промені мають однакову кінцеву точку. Вершина є загальною кінцевою точкою двох променів, які утворюють кут. Сторони - це два промені, які утворюють кут.

F-д_532ФБ 1973E686515C84D028BCD4707142БК 0АД 04544429Ф5А3502003+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

*Позначте це*	*Скажи це*
\(\angle ABC\)	Кут\(ABC\)
\(\angle CBA\)	Кут\(CBA\)

Вершина є,\(B\) а сторони -\(\overrightarrow{BA}\) і\(\overrightarrow{BC}\). Завжди використовуйте три літери, щоб назвати кут,\(\angle\) SIDE-VERTEX-SIDE.

Кути вимірюються чимось, званим транспортиром. Транспортир - це вимірювальний прилад, який вимірює, наскільки «відкритий» кут. Кути вимірюються в градусах і маркуються\( ^{\circ}\) символом. Наразі кути завжди позитивні.

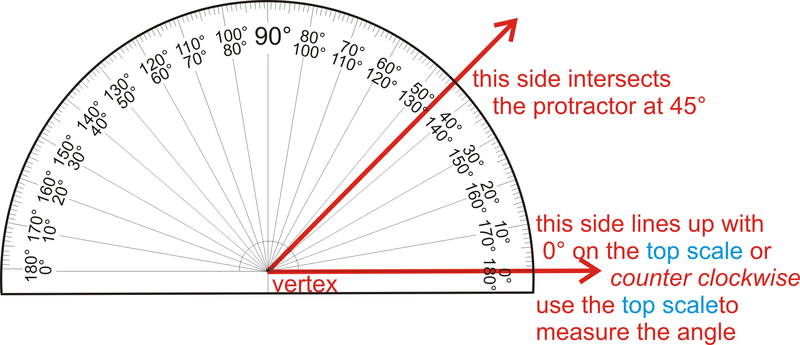
F-D_58316B563A8093F47D8C272 ФБ 48356C11763 ББ655ФБ9392AFC8F07+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Є два набори вимірювань, один починається зліва, а інший з правого боку транспортира. Обидва йдуть навколо від\( 0 ^{\circ}\) до\(180 ^{\circ}\). При вимірюванні кутів можна вирівняти одну сторону з\( 0 ^{\circ}\), і подивитися, де інша сторона потрапляє на транспортир. Вершина лінії вгору посередині лінії низу.

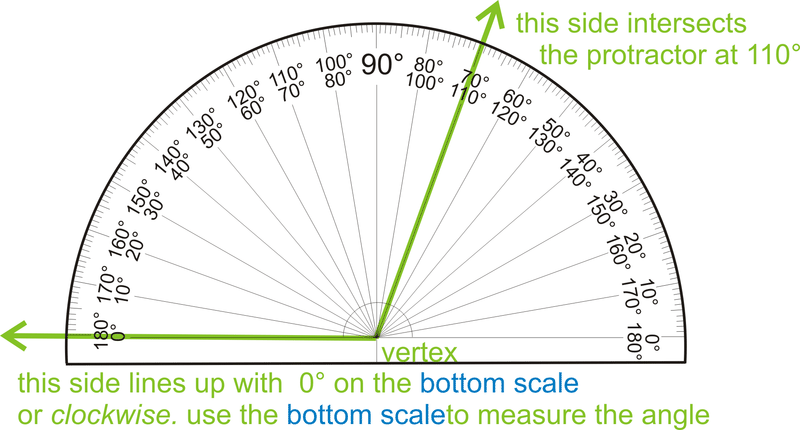
Ф-д_Е52Д0ФБ66ББ1Ф14Д56908Б14Д1д60351450157ФЦ702Д1494203Д94А+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

Зверніть увагу, що якщо ви не вирівнюєте одну сторону з\( 0 ^{\circ}\), міра кута буде різницею градусів, де сторони кута перетинаються з транспортиром.

Іноді вам захочеться намалювати кут, який є певною кількістю градусів. Виконайте наведені нижче дії, щоб намалювати\( 50 ^{\circ}\) кут за допомогою транспортира:

Почніть з малювання горизонтальної лінії по всій сторінці, довжиною 2 дюйма.

Ф-Д_БК 9А807Д4554Ф1ФД86БА 28968 БД6Ф7А627Е4А35Е0А514Е56А106321С+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{4}\)

Помістіть кінцеву точку в лівій частині лінії.
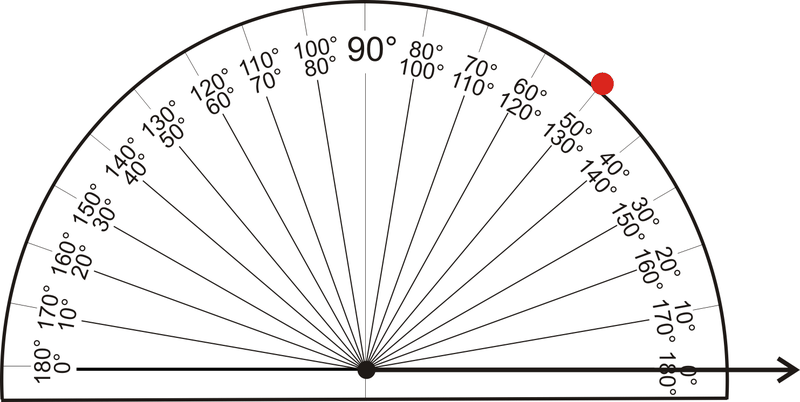
Помістіть транспортир на цю точку, таким чином, щоб лінія проходила через\( 0 ^{\circ}\) мітку на транспортирі, а кінцева точка виявилася в центрі. Відзначте\( 50 ^{\circ}\) на відповідній шкалі.

F-D_57BDF 0ЕЕ2 ДДІ 38АЕ44А7Д5Д768 Е58АФ940А3С2ЕД55Д93Д93Б70+зображення_крихіткий+зображення_крихіткий.PNG

Зніміть транспортир і з'єднайте вершину і\(50 ^{\circ}\) mark.

f-d_9837a241ce1d8148a64653cd933ce66a6974e86e98e434b60281a013+IMAGE_TINY+IMAGE_TINY.png — Figure \(\PageIndex{6}\)

This process can be used to draw any angle between \(0 ^{\circ}\) and \(180 ^{\circ}\).

When two smaller angles form to make a larger angle, the sum of the measures of the smaller angles will equal the measure of the larger angle. This is called the Angle Addition Postulate. So, if B is on the interior of \(\angle ADC\), then

\(\angle ADC = m \angle ADB + \angle BDC\)

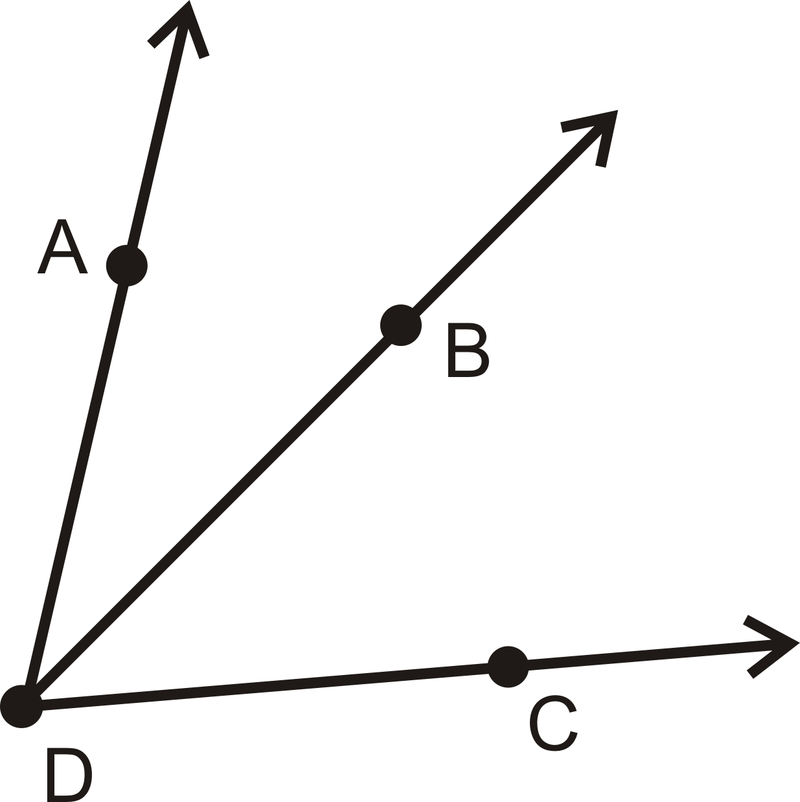f-d_0f6199a5ebc5624520885acb44e3a5697c32ac975c9ce445bb21ff9c+IMAGE_TINY+IMAGE_TINY.png — Figure \(\PageIndex{7}\)

Example \(\PageIndex{1}\)

How many angles are in the picture below? Label each one.

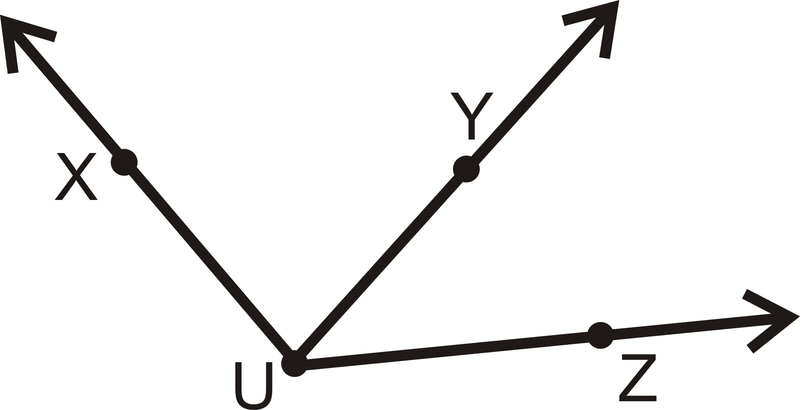f-d_f30e476dc5d7133a018599e9880692c4f36da6d84bd1170f35ea342d+IMAGE_TINY+IMAGE_TINY.png — Figure \(\PageIndex{8}\)

Solution

There are three angles with vertex \(U\). It might be easier to see them all if we separate them.

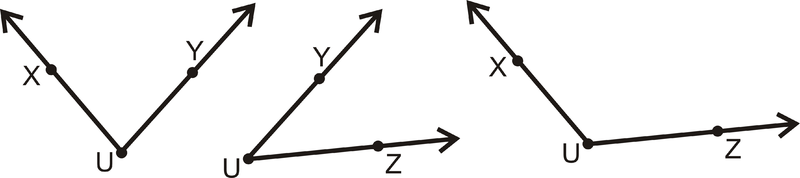f-d_1188b4311dd28d72313b56cc7cb49e863f7495e23542ecc712e8fea6+IMAGE_TINY+IMAGE_TINY.png — Figure \(\PageIndex{9}\)

So, the three angles can be labeled, ( \(\angle XUY\) or \(\angle YUX\)), \(\angle YUZ\) (or \(\angle ZUY\)), and \(\angle XUZ\) (or \(\angle ZUX\)).

Example \(\PageIndex{2}\)

Measure the three angles from Example 1, using a protractor.

Solution

Just like in Example 1, it might be easier to measure these three angles if we separate them.

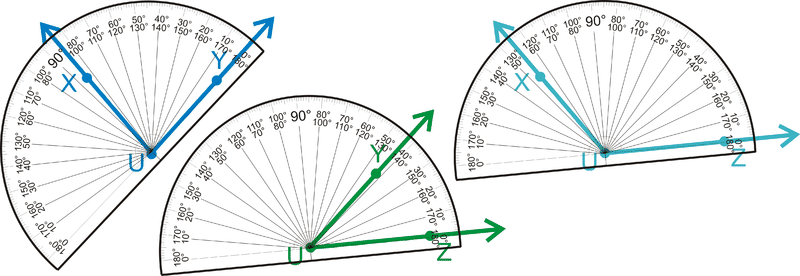f-d_01e38d5f6305c6b637bd27e75ef0c99d2c9524a5acec6aceedf70e99+IMAGE_TINY+IMAGE_TINY.png — Figure \(\PageIndex{11}\)

With measurement, we put an m in front of the \(\angle\) sign to indicate measure. So, \(m \angle XUY = 84^{\circ}\), \(m \angle YUZ = 42^{\circ}\) and \(m \angle XUZ = 126^{\circ}\).

Example \(\PageIndex{3}\)

What is the measure of the angle shown below?

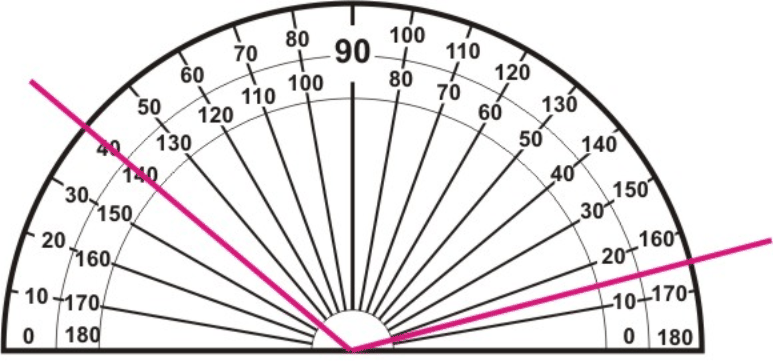f-d_0d12297fa3f159e0deb25e56df631c0025da3423e276387da8395f58+IMAGE_TINY+IMAGE_TINY.png — Figure \(\PageIndex{12}\)

Solution

This angle is not lined up with 0∘, so use subtraction to find its measure. It does not matter which scale you use, as long as you are consistent.

Inner scale: \(140^{\circ} - 15 ^{\circ} = 125 ^{\circ}\)

Outer scale: \(165^{\circ} - 40 ^{\circ} = 125 ^{\circ}\)

Example \(\PageIndex{4}\)

Use a protractor to measure \(\angle RST\) below.

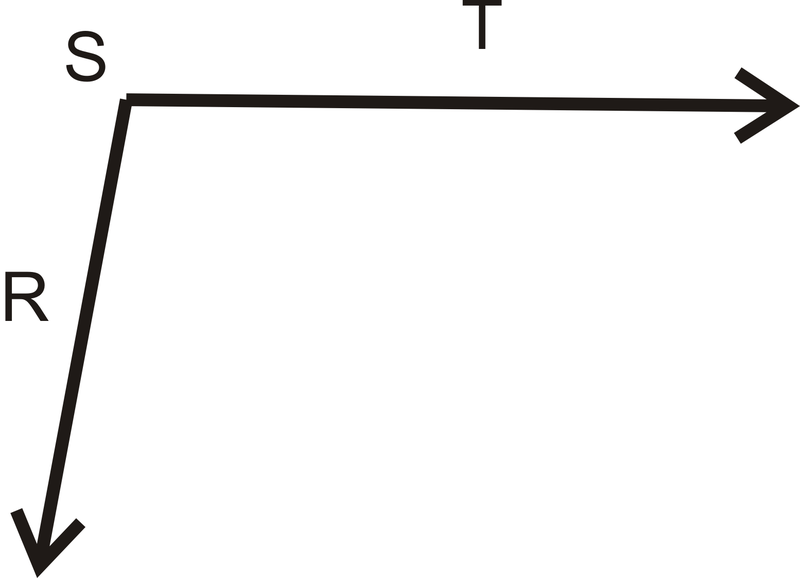f-d_09846946f12d23b3c78ff6f798a97760fc030557387e4951feda9c9c+IMAGE_TINY+IMAGE_TINY.png — Figure \(\PageIndex{13}\)

Solution

Lining up one side with \(0 ^{\circ}\) on the protractor, the other side hits \(100 ^{\circ}\).

Example \(\PageIndex{5}\)

What is \(m \angle QRT\) in the diagram below?

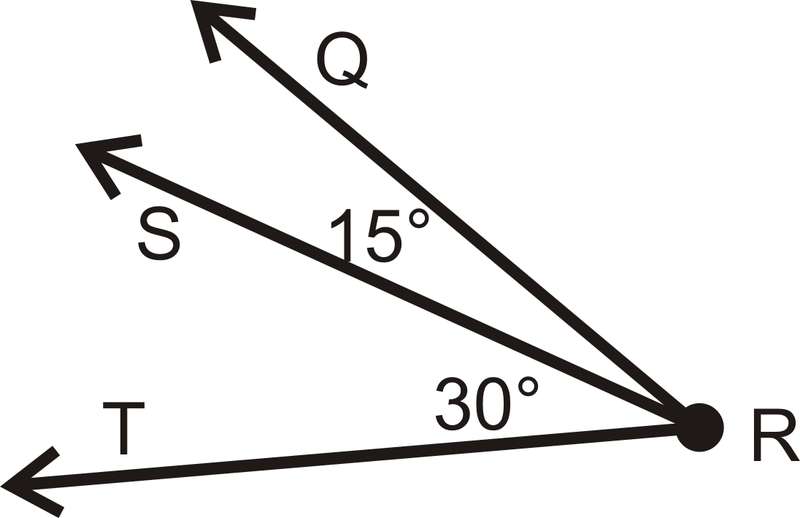f-d_70bd9c47f610a75d13359170faaac772c71e15c49c78336fd40f5447+IMAGE_TINY+IMAGE_TINY.png — Figure \(\PageIndex{14}\)

Solution

Using the Angle Addition Postulate, \(m\angle QRT = 15^{\circ}+30^{\circ}=45^{\circ}\).

Review

1. What is \(m \angle LMN\) if \(m \angle LMO = 85^{\circ}\) and \(m \angle NMO = 53^{\circ}\)?

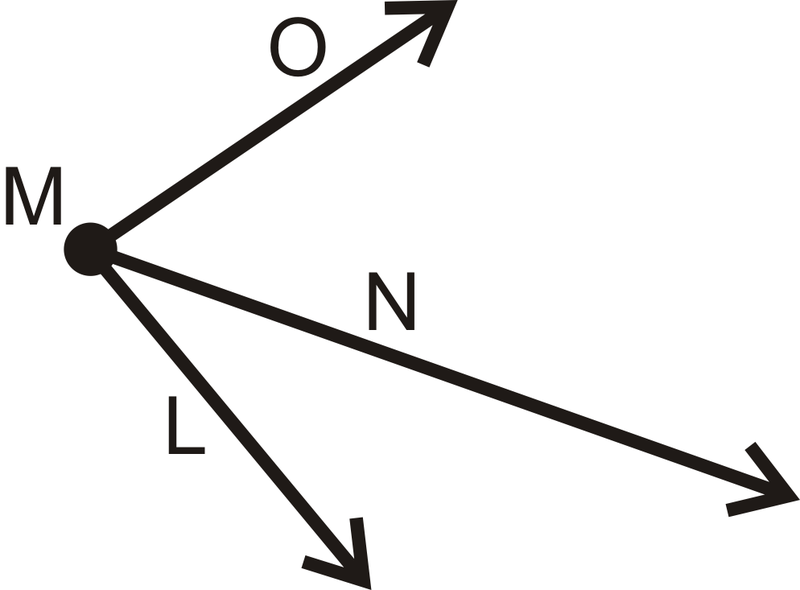f-d_4e0ea786ec8e3b32c7c5661b4054720f0c401334e4df18d56d797b6b+IMAGE_TINY+IMAGE_TINY.png — Figure \(\PageIndex{15}\)

2. If \(m \angle ABD = 100^{\circ}\), find \(x\).

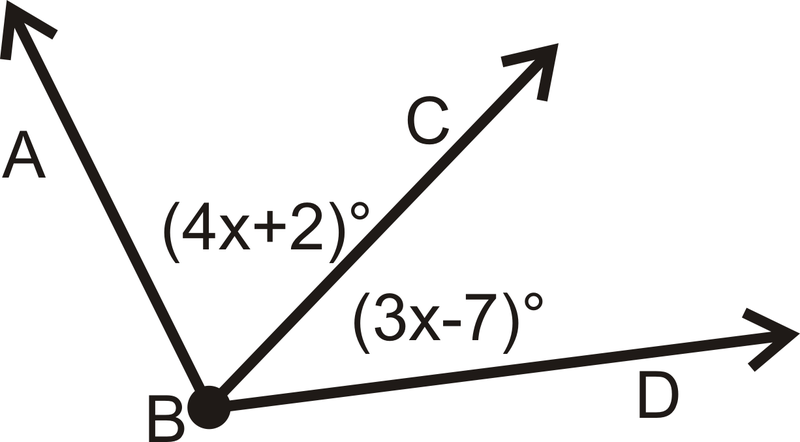f-d_b3ca9a5513c6c31de0ef3d495eb278ff8caa8cc852c57d37706cd575+IMAGE_TINY+IMAGE_TINY.png — Figure \(\PageIndex{16}\)

For questions 3-6, determine if the statement is true or false.

For an angle \(\angle ABC\),\(C\) is the vertex.
For an angle \(\angle ABC\), \(\overline{AB}\) and \(\overline{BC}\) are the sides.
The \(m\) in front of \(m \angle ABC\) means measure.
The Angle Addition Postulate says that an angle is equal to the sum of the smaller angles around it.

For 7-12, draw the angle with the given degree, using a protractor and a ruler.

\(55 ^{\circ}\)
\(92 ^{\circ}\)
\(178 ^{\circ}\)
\(5 ^{\circ}\)
\(120 ^{\circ}\)
\(73 ^{\circ}\)

For 13-16, use a protractor to determine the measure of each angle.

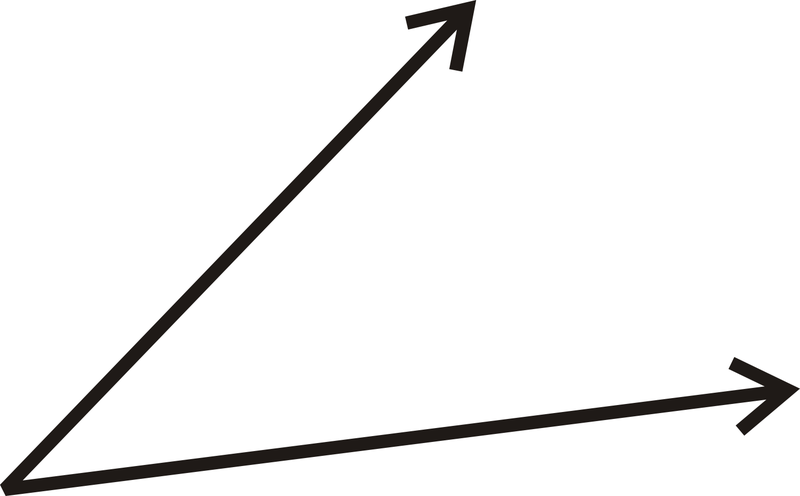Figure \(\PageIndex{17}\)
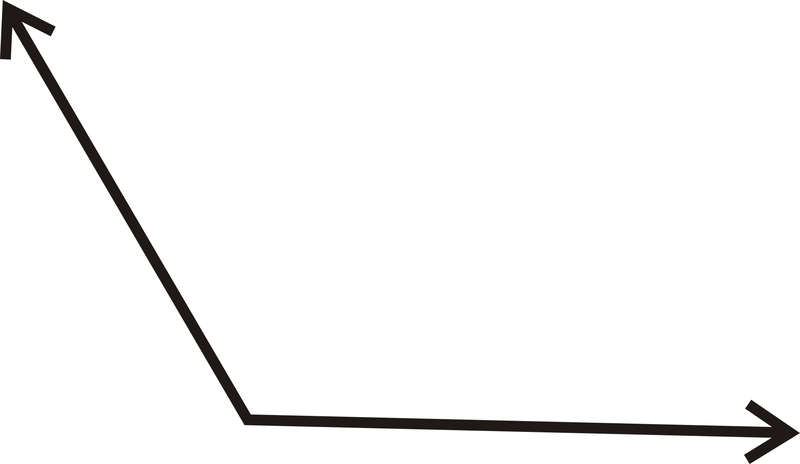Figure \(\PageIndex{18}\)
Figure \(\PageIndex{19}\)
Figure \(\PageIndex{20}\)

Solve for \(x\).

\(m \angle ADC = 56^{\circ}\)

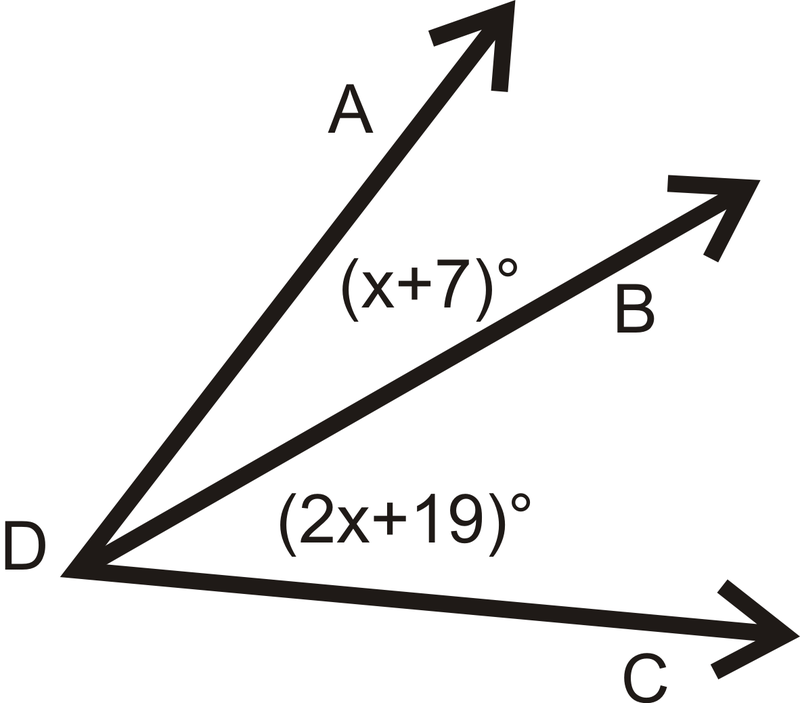f-d_2e3dc68cf631e91c426a771b5dff70af2d5ffddd4e8c4f8eeb874523+IMAGE_TINY+IMAGE_TINY.png — Figure \(\PageIndex{21}\)

Review (Answers)

To see the Review answers, open this PDF file and look for section 1.5.

Vocabulary

Term	Definition
Angle	A geometric figure formed by two rays that connect at a single point or vertex.
Protractor	A protractor is a tool used to measure an angle in terms of degrees.
Vertex	A vertex is a point of intersection of the lines or rays that form an angle.

Additional Resource

Interactive Element

Video: Angle Basics

Activities: Angle Measurement Discussion Questions

Study Aids: Angles Study Guide

Practice: Measuring Angles

Real World: Angle Measurement