5.4.1: Векторне рівняння прямої

Last updated
Save as PDF

Page ID: 55150

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Векторне рівняння прямої

Управління повітряним рухом веде стеження за двома літаками в безпосередній близькості від їх аеропорту. На даний момент один літак знаходиться в локації 45 км на схід і 120 км на північ від аеропорту на висоті 7,5 км. Другий літак розташований в 63 км на схід і в 96 км на південь від аеропорту на висоті 6,0 км. Перший літак летить безпосередньо до аеропорту, тоді як другий літак триває на постійній висоті з курсом, визначеним вектором,\(\ \overrightarrow{h_{2}}=\langle 3,4,0\rangle\) щоб приземлитися в кінцевому підсумку в іншому аеропорту на північний захід від наших диспетчерів повітряного руху. Чи перетинаються шляхи цих двох літаків?

Векторне рівняння прямої

Ви, мабуть, дуже знайомі з використанням y = mx + b, форми нахилу -перехоплення, як рівняння прямої. Хоча це рівняння добре працює в двовимірному просторі, його недостатньо для повного визначення рівняння прямої у просторах вищого порядку.

Лінії в просторі

У двовимірній площині пряму можна представити рівнянням y = mx + b, де m - нахил прямої і b - y-перехоплення. У тривимірному просторі це рівняння може представляти лінію або площину або проекцію тривимірної лінії на площину xy. Наприклад, на схемі нижче лінія зліва проходить через точки Р і Q. рівняння в 2D просторі для цієї лінії дорівнює\(\ y=\frac{-P}{Q} x+P\)

Три помаранчеві лінії на діаграмі праворуч нижче також можуть бути описані цим рівнянням. Всі три мають нахил\(\ M=\frac{-P}{Q}\) і y-перехоплення B = P. Якщо ми хочемо вказати одну з цих ліній зокрема, нам потрібно визначити лінію як перетин двох площин. Наприклад, лінія, де\(\ y=\frac{-P}{Q} x+P\) і\(\ z=0\) для всіх точок - це перетин помаранчевої та зеленої площин на схемі внизу праворуч. (Пам'ятайте, що помаранчева і зелена площини намальовані краями для зручності, але що вони представляють площини, які простягаються назовні до нескінченності.)

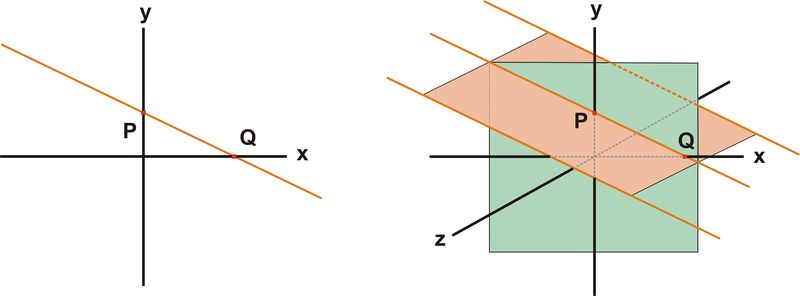
Ф-Д_87Д3ЕФ 264 АБС 5АСЕ 1ДБ2265 ФАБ154Б4С1Е02Е8А6Б303298 АА983ЕФ+зображення_крихіткий+зображення_крихіткий.jpg

Тому ми можемо вказати певну лінію, вимагаючи, щоб рівняння для обох площин були одночасно істинними. У попередньому розділі ми розробили одне рівняння для площини, заданої d = - n _x x _o - n _y y _o - n _з з _о. При цьому Qy + Px - QP = 0 і z = 0 повинні бути виконані для всіх точок на прямій, що проходить через точки P і Q.

Пошук векторного рівняння прямої

Інший спосіб ідентифікації точок на прямій можна знайти за допомогою методу додавання векторів, про який ми говорили раніше в цьому розділі. Щоб знайти вектор положення\(\ \vec{r}\), для будь-якої точки вздовж лінії, ми можемо додати вектор положення точки на лінії, яку ми вже знаємо, і додати до цього вектор\(\ \vec{v}\), який лежить на лінії, як показано на схемі нижче.

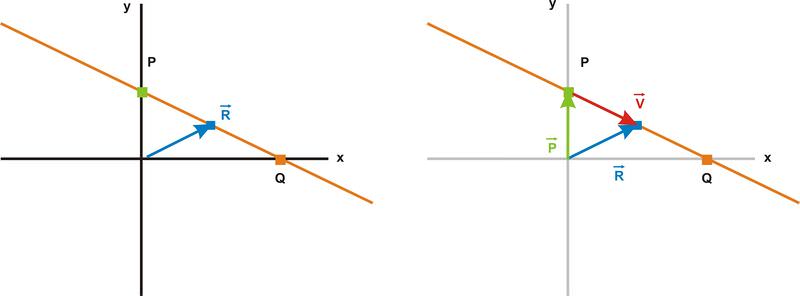
Ф-Д_Ф 48Б142 ЕБ5Д67815285Е9Д9Е50Б98С0А84 ЕДДФ 653187А8Б58Б4Е351+зображення_крихіткий+зображення_крихіткий.JPG

Вектор положення\(\ \vec{R}\) для точки між P і Q задається\(\ \vec{R}=\vec{p}+\vec{v}\)

Всі інші точки на цій лінії можуть бути досягнуті шляхом переміщення по лінії з точки Р, тому вектор положення для будь-якої точки на прямій задається\(\ \vec{r}=\vec{p}+k \vec{v}\).

Якщо ми знаємо розташування двох точок на прямій, ми можемо визначити рівняння прямої. Усі точки на прямій виконують рівняння\(\ \vec{r}=\vec{p}+k \vec{v}\), де k - скаляр, який змінюється від -∞ до ∞. Якщо ми вже знаємо вектори положення для двох точок на прямій,\(\ \vec{p}\) причому\(\ \vec{q}\), ми можемо використовувати метод векторного віднімання для визначення рівняння вектора,\(\ \vec{v}=\vec{p}-\vec{q}\). Тому\(\ \vec{r}=\vec{p}+k(\vec{p}-\vec{q})\), де k варіюється від -∞ до ∞.

Загальні векторні рівняння

Взагалі, векторне рівняння - це будь-яка функція, яка приймає будь-яку одну або кілька змінних і повертає вектор. Векторне рівняння прямої - це рівняння, яке ідентифікує вектор положення кожної точки вздовж лінії. Це працює для прямих ліній і для кривих. Наприклад, векторне рівняння\(\ \vec{p}=\langle 3 \cos \theta, 3 \sin \theta, 2\rangle\) визначає коло, що має радіус 3 одиниці, яка сидить паралельно площині xy на відстані 2 одиниці вздовж осі z, як показано нижче. Помаранчева лінія - це множина точок, які задовольняють векторному рівнянню,\(\ \vec{p}=\langle 3 \cos \theta, 3 \sin \theta, 2\rangle\) тоді як сірі лінії - різні окремі вектори положення, які задовольняють векторному рівнянню.

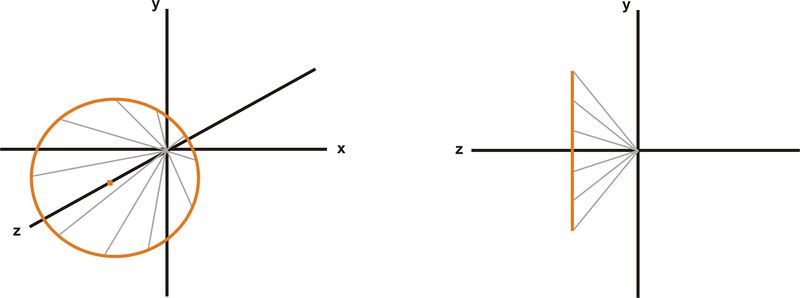
F-D_37D77040Б05ББ Б 19Д42С3Ф68Е 3497Б АФ 0CD1B2C7332199D97+зображення_крихіткий+зображення_крихіткий.jpg

Приклади

Приклад 1

Раніше вам задавали питання про два літаки.

Рішення

Перше, що нам потрібно зробити, це визначити вектори положення двох площин. Визначте наш аеропорт як координати походження і визначити\(\ \hat{x}=\text { east }\)\(\ \hat{y}=\text { north }\), і\(\ \hat{z}=\text { upward }\). Викликати положення площини #1, P і положення площини #2, Q. Це дає\(\ \vec{p}=\langle 45,120,7.5\rangle\) і\(\ \vec{q}=\langle 63,-96,6.0\rangle\).

Літак #1 прямує безпосередньо до аеропорту. Вектор від позиції площини #1 до початку задано

\ (\\ почати {масив} {l}
\ vec {v} =\ vec {o} -\ vec {p} =\ лангле (0-45), (0-120), (0-7.5)\ діапазон\
\ vec {v} =\ vec {p} -\ vec {q} =\ лангл-45, -120, -7.5\ діапазон
\ кінець {масив}\)

Рівняння лінії, що представляє рух площини #1, потім стає

\(\ \overrightarrow{r_{1}}=\langle 45,120,7.5\rangle+k_{1}\langle-45,-120,-7.5\rangle \quad \overrightarrow{r_{1}}=\langle 45,120,7.5\rangle+k_{1}\langle-45,-120,-7.5\rangle\)

Літак #2 триває на постійній висоті з курсом\(\ \overrightarrow{h_{2}}=\langle 3,4,0\rangle\). Рівняння лінії, що представляє рух площини #2, потім стає

\ (\\ begin {масив} {l}
\ vec {r} _ {2} =\ ланг-63,96,0\ діапазон+k_ {2}\ кут 3,4,0\ діапазон\ квадратний\ переправа стрілка {r_ {2}} =\ лангл 63, -96,0\ діапазон+k_ {2}\ langle 3,4,0\ діапазон
\\ переправа стрілка {r_ {2}} =\ лангу-63,96,0\ діапазон+k_ {2}\ кут 3,4,0\ діапазон\\
\ переправа стрілка {r_ {1}} =\ лангле 45,120,7.5\ діапазон+k_ {1}\ ланг-45, -120, -7.5\ діапазон
\ кінець {масив}\)

Якщо шляхи двох площин перетинаються, положення цього перетину повинно мати координати, які задовольняють обом рівнянням.

Щоб задовольнити обидва рівняння, r ₁ _x повинен дорівнювати r ₂ _x, r ₁ _y повинен дорівнювати r ₂ _y, а r ₁ _z повинен дорівнювати r ₂ _z. Це означає, що 45 - 45 к ₁ = 63 + 3 к ₂, 120 - 120 к ₁ = -96 + 4 к ₂, і 7,5 - 7,5 к ₁ = 6,0 + 0 k ₂ повинні бути одночасно істинними.

Перше рівняння спрощує до 15 - 15 k ₁ = 21 + k ₂ або k ₂ = -6 - 15 k ₁. Другий спрощує до 30 - 30 к ₁ = -24 + к ₂ або k ₂ = 54 - 30 к ₁. Третє рівняння спрощує до 7,5 - 7,5 к ₁ = 6 або\(\ k_{1}=\frac{1}{5}\).

Вставивши значення k ₁ з третього рівняння в перші два рівняння, знаходимо\(\ k_{2}=-6-15\left(\frac{1}{5}\right)=-6-3=-9 \text { and } k_{2}=54-30 k_{1}=54-30\left(\frac{1}{5}\right)=54-6=48\)

Оскільки k ₂ = 33 і k ₂ = 0 не можуть бути одночасно істинними, шляхи двох площин не перетинаються.

Примітка: Існують інші способи причини через цю проблему. Ви можете знайти деякі? (Підказка: Подумайте про геометрію в 2-х вимірах або зосередьтеся на висоті як спосіб спростити цю проблему).

Приклад 2

Запишіть рівняння\(\ y=-\frac{5}{3} x+5\) як векторне рівняння.

Рішення

Почніть з вибору двох точок на лінії, скажімо\(\ (3,0)\) і\(\ (6,-5)\). Тоді\(\ \vec{p}=\langle 3,0\rangle\) і\(\ \vec{q}=\langle 6,-5\rangle\) так,

\(\ \vec{p}-\vec{q}=\langle 3,0\rangle-\langle 6,-5\rangle=\langle 3-6,0-(-5)\rangle=\langle-3,5\rangle\)

Нарешті, векторне рівняння прямої

\(\ \vec{r}=\langle 3,0\rangle+k\langle-3,5\rangle=\langle 3-3 k, 5 k\rangle\)

Приклад 3

Запишіть векторне рівняння прямої, визначеної точками (2, 3, 4) і (-5, 2, -1).

Рішення

Ці дві точки мають вектори положення ⟨2,3,4⟩ та ⟨−5,2, −1⟩. Вектор лінії, що з'єднує дві точки, задається

\ (\\ почати {масив} {l}
\ vec {v} =\ vec {p} -\ vec {q} =\ ланголь (2- (-5)), (3-2), (4- (-1))\ діапазон
\\ капелюх {v} =\ vec {p} -\ vec {q} =\ лангл 7,1,5
\ кінець {масив}\)

Рівняння прямої тоді стає

\(\ \vec{r}=\langle 2,3,4\rangle+k\langle 7,1,5\rangle \quad \vec{r}=\langle 2,3,4\rangle+k\langle 7,1,5\rangle\)

Приклад 4

Визначте рівняння для прямої, визначеної точками Р = (6, 7, 5) і Q = (3, 2, 11). Потім знайдіть вектор положення для точки, R, на півдорозі між цими двома точками.

Рішення

\ (\\ почати {масив} {l}
\ vec {v} =\ vec {p} -\ vec {q} =\ ланголь (6-3), (7-2), (5-11)\ діапазон\
\ hat {v} =\ vec {p} -\ vec {q} =\ лангель 3,5, -6\ діапазон
\ кінець {масив}\)

Рівняння прямої тоді стає

\(\ \vec{r}=\langle 6,7,5\rangle+k\langle 3,5,-6\rangle \quad \vec{r}=\langle 6,7,5\rangle+k\langle 3,5,-6\rangle\)

Оскільки вектор\(\ \vec{v}\) вказує від P, значення k для певної точки дає нам деяку інформацію про розташування цієї точки. Якщо 0 < k < 1, точка лежить на лінії між P і Q. Якщо k < 0, точка знаходиться не між P і Q і ближче до P, ніж Q. Якщо k > 1, точка лежить на лінії між P і Q. Якщо k < 0, точка знаходиться не між P і Q і ближче до P, ніж Q. Точка на півдорозі між двома точками має\(\ k=\frac{1}{2}\).

\ (\\ почати {масив} {l}
\ vec {R} =\ лангле 6,7,5\ діапазон+\ розрив {1} {2}\ кут 3,5, -6\ діапазон\
\ vec {R} =\ кут (6+1.5), (7+2.5), (5+ (-3)\ діапазон =\ langle 7.5,9.5,2\ кут
\ кінець {масив}\)

Приклад 5

Чи два вектори\(\ \vec{D}=\langle 1,-1,4\rangle+d\langle 1,-1,1\rangle\) та\(\ \vec{F}=\langle 2,4,7\rangle+f\langle 2,1,3\rangle\) перекісні лінії чи вони перетинаються один з одним?

Рішення

Якщо два вектори перетинаються, має бути точка, ідентифікована вектором положення\(\ \vec{p}\), яка задовольняє рівнянням обох рядків. Іншими словами, ми повинні вміти знаходити значення для d і f такі, що\(\ \vec{D}=\vec{F}\) або\(\ \langle 1,-1,4\rangle+d\langle 1,-1,1\rangle=\langle 2,4,7\rangle+f\langle 2,1,3\rangle\).

Кожна з трьох складових векторів\(\ \vec{D}\) і\(\ \vec{F}\) повинна незалежно бути рівними якщо\(\ \vec{D}=\vec{F}\). Це означає, що 1 + d = 2 + 2 f, -1 - d = 4 + f, а 4 + d = 7 + 3 f Поєднання перших двох рівнянь дає: 1 + d - 1 - d = 2 + 2 f + 4 + f який при спрощенні стає 0 = 6 + 3 f або f = -2. Якщо ми підставимо це назад у перше рівняння, яке ми отримаємо, 1 + d = 2 + 2 (-2), яке при спрощенні стає d = -3. Якщо два рядки перетинаються, f = -2 і d = -3 повинні задовольнити кожне з складових рівнянь.

1 + d = 2 + 2 f стає 1 + (-3) = 2 + 2 (-2) або -2 = -2

-1 - d = 4 + f стає -1 - (-3) = 4 + (-2) або +2 = +2

4 + d = 7 + 3 f стає 4 + (-3) = 7 + 3 (-2) або +1 = +1

Всі три рівняння однаково задоволені, тому дві лінії перетинаються і точка перетину дорівнює (-2, 2, 1).

Приклад 6

У фізиці рух об'єкта, що рухається з постійною швидкістю, описується рівнянням,\(\ \overrightarrow{s_{t}}=\overrightarrow{s_{i}}+\vec{v} t\) де s _i - початкове положення, s - положення в якийсь більш пізній час t, а v це швидкість руху об'єкта. Запишіть векторне рівняння, яке повертає набір векторів положення\(\ \vec{s}\) для об'єкта, що має початкове положення\(\ \overrightarrow{s_{i}}=\langle 2,3,4\rangle\)\(\ \vec{v}=\langle 1,1,-2\rangle\) та швидкість, і визначте місце розташування об'єкта при t = 10s.

Рішення

\ (\\ почати {масив} {l}
\ переправа стрілка {s_ {t}} =\ переправа стрілка {s_ {i}} +\ vec {v} t =\ кут 2,3,4\ діапазон+t\ langle 1,1, -2\ діапазон =\ langle 2+t, 3+t, 4-2 t\ діапазон\
\\ текст {At} t = 10 s,\ переправа стрілка {s_ {10}} =\ кут 2+10,3+10,4-2 (10)\ діапазон =\ кут 12,13, -16\ діапазон
\ кінець {масив} \)

Приклад 7

Об'єкт має положення\(\ \overrightarrow{s_{i}}=\langle 3,3,6\rangle\) at t = 0 і швидкість\(\ \vec{v}=\langle 10,7,3\rangle\). Використовуйте векторне рівняння,\(\ \vec{s}=\overrightarrow{s_{i}}+\vec{v} t\) щоб визначити відстань, пройдену об'єктом між t = 3s і t = 5s. Відстань вимірюється в метрах.

Рішення

Векторне рівняння, що описує рух об'єкта

\(\ \vec{s}=\vec{s}_{i}+\vec{v} t=\langle 3,3,6\rangle+t\langle 10,7,3\rangle=\langle 3+10 t, 3+7 t, 6+3 t\rangle\)

Положення об'єкта при t = 3s виходить з векторного рівняння:

\(\ \overrightarrow{s_{3}}=\overrightarrow{s_{i}}+\vec{v} t=\langle 3,3,6\rangle+(3)\langle 10,7,3\rangle=\langle 3+10(3), 3+7(3), 6+3(3)\rangle=\langle 33,24,15\rangle\)

Положення об'єкта при t = 5s виходить з векторного рівняння:

\(\ \overrightarrow{s_{5}}=\overrightarrow{s_{i}}+\vec{v} t=\langle 3,3,6\rangle+(5)\langle 10,7,3\rangle=\langle 3+10(5), 3+7(5), 6+3(5)\rangle=\langle 53,38,21\rangle\)

Відстань, пройдена між цими двома точками, - це величина вектора, починаючи з (33, 24, 15) і закінчуючи на (53, 38, 21).

\(\ \overrightarrow{\triangle s}=\overrightarrow{s_{5}}-\overrightarrow{s_{3}}=\langle 53,38,21\rangle-\langle 33,24,15\rangle=\langle 20,14,6\rangle\)

Тепер ми можемо використовувати теорему Піфагора для визначення величини вектора.

\(\ \overrightarrow{|\triangle s|}=\sqrt{a^{2}+b^{2}+c^{2}}=\sqrt{(20)^{2}+(14)^{2}+(6)^{2}}=25.1 \text { meters }\)

Приклад 8

Визначте векторне рівняння прямої, визначеної точками (2, 2, 2) і (1, 3, 5).

Рішення

Ці дві точки мають вектори положення\(\ \vec{p}=\langle 2,2,2\rangle\) і\(\ \vec{q}=\langle 1,3,5\rangle\). Вектор лінії, що з'єднує дві точки, задається

\(\ \vec{v}=\vec{p}-\vec{q}=\langle(2-1),(2-3),(2-5)\rangle=\langle 1,-1,-3\rangle\)

Рівняння прямої\(\ \vec{r}=\vec{p}+k \vec{v}\), потім стає

\(\ \vec{r}=\langle 2,2,2\rangle+k\langle 1,-1,-3\rangle \quad \vec{r}=\langle 2,2,2\rangle+k\langle 1,-1,-3\rangle\)

Приклад 9

Чи дві лінії\(\ \vec{R}=\langle 4,4,-2\rangle+r\langle-3,7,2\rangle\) і\(\ \vec{K}=\langle 9,-8,7\rangle+k\langle-2,1,3\rangle\) перетинаються?

Рішення

Якщо два вектори перетинаються, має бути точка, ідентифікована вектором положення\(\ \vec{p}\), яка задовольняє рівнянням обох рядків. Іншими словами, ми повинні бути в змозі знайти значення для r і k такі, що

\(\ \vec{R}=\vec{K}\)або\(\ \langle 4,4,-2\rangle+r\langle-3,7,2\rangle=\langle 9,-8,7\rangle+k\langle-2,1,3\rangle\).

Кожна з трьох складових векторів\(\ \vec{R}\) і\(\ \vec{K}\) повинна незалежно бути рівними якщо\(\ \vec{R}=\vec{K}\). Це означає, що 4 - 3 р = 9 - 2 к, 4 + 7 р = -8 + к, а -2 + 2 р = 7 + 3 к

Розв'язування другого рівняння для k дає 12 + 7 r = k. Тепер підставляємо це в одне з двох інших рівнянь: 4 - 3 r = 9 - 2 (12 + 7 r) або 4 - 3 r = 9 - 24 - 14 r, що спрощує до 19 = -11 р або\(\ r=\frac{-19}{11}=-1.727\). Підставляємо це значення в одне з інших рівнянь: -2 + 2 (-1,727) = 7 + 3 k, яке стає -2 - 3,454 = 7 + 3 к. Розв'язування для k дає k = -4.151. Якщо дві лінії перетинаються, r = -1.727 і k = -4.151 повинні задовольнити кожне з рівнянь складових.

4 - 3 r = 9 - 2 k стає 4 - 3 (-1,727) = 9 - 2 (-4,151) або -1,181 = 17,302 Так як навіть це перше рівняння не відповідає дійсності, ці дві лінії перекошені і не перетинаються.

Рецензія

Запишіть векторне рівняння прямої, визначеної наступними точками:

(2, −2,5) і (1,5,4)
(2, −9,5) та (8,4, −6)
(15,3, −3) і (4, −3,9)
(−1, −1,7) та (3,11,8)
(1, −3,2) та (−5,3, −1)
(25,17,42) і (−16,12,23)

Визначте, чи два вектори є косими лініями або вони перетинаються один з одним.

\(\ \vec{D}=\langle 2,3,1\rangle+d\langle 5,3,6\rangle\)і\(\ \vec{F}=\langle-5,-3,-5\rangle+f\langle 15,3,-3\rangle\)
\(\ \vec{D}=\langle 3,4,7\rangle+d\langle 3,3,2\rangle\)і\(\ \vec{F}=\langle-2,11,7\rangle+f\langle-2,11,7\rangle\)
\(\ \vec{D}=\langle 15,3,-3\rangle+d\langle 3,11,8\rangle\)і\(\ \vec{F}=\langle 5,3,6\rangle+f\langle 1,-4,6\rangle\)
\(\ \vec{D}=\langle 13,-1,6\rangle+d\langle-5,4,12\rangle\)і\(\ \vec{F}=\langle 6,9,0\rangle+f\langle 21,0,14\rangle\)

Визначте вектор положення для середньої точки кожного рядка (векторні рівняння ви вже знайшли в задачах з 1 по 4).

(2, −2,5) і (1,5,4)
(2, −9,5) та (8,4, −6)
(15,3, −3) і (4, −3,9)
(−1, −1,7) та (3,11,8)

Використовуйте векторне рівняння і наступні значення для t: t = 3s і t = 5s. Відстань вимірюється в метрах.

Об'єкт має позицію\(\ \overrightarrow{s_{i}}=\langle 3,-5,1\rangle\) at t = 0 і швидкість\(\ \vec{v}=\langle 2,7,-3\rangle\)
Об'єкт має позицію\(\ \overrightarrow{s_{i}}=\langle 1,-4,-8\rangle\) at t = 0 і швидкість\(\ \vec{v}=\langle 9,-7,3\rangle\)
Об'єкт має позицію\(\ \overrightarrow{s_{i}}=\langle-1,2,-3\rangle\) at t = 0 і швидкість\(\ \vec{v}=\langle 3,-1,-2\rangle\)

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 5.10.

Лексика

Термін	Визначення
вектор положення	Вектор положення описує пряму лінію між початковою точкою (зазвичай початковою точкою) і розташуванням другої точки на координатній площині.
Лінії перекісу	Перекісні лінії - це лінії, які знаходяться в різних площинях і ніколи не перетинаються.
векторне рівняння	Векторне рівняння - це будь-яка функція, яка приймає будь-яку одну або кілька змінних і повертає вектор.