5.3.2: Векторний напрямок

Векторний напрямок

Алісса любить фізику, і її зачаровує те, що існують розрахунки для всіх фізичних взаємодій і рухів у навколишньому світі. У п'ятницю Алісса вирушила на ярмарок округу зі своїм хлопцем Куртом, який вирішив, що буде романтично, якщо він зможе виграти її гігантську опудалу в грі з нокдауну. На жаль для Курта, він все ще нічого не збив приблизно за 45 хвилин і 35 доларів пізніше.

Алісса вирішує спробувати сама, і розуміє, що центр банок - це єдина позиція в просторі. Якщо Алісса знає власну висоту кидання та відстань, яку банки укладені за лінією метання, що ще їй потрібно знати, щоб обчислити вектори, пов'язані з прямою лінією шляху для м'яча? Як би вона їх розрахувала?

---

Векторний напрямок

Нагадаємо, що рівняння для вектора задається

$\ \vec{p}=\left\langle P_{x}, P_{y}, P_{z}\right\rangle$

де P _x, P _y та P _z - координати x, y та z вектора, отримані проектуванням вектора на осі x, y та z, як показано нижче ліворуч.

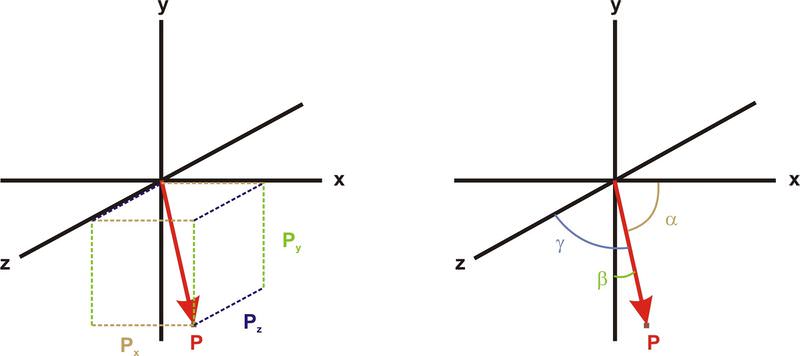
Зображення вгорі праворуч показує кути між вектором положення та трьома осями: α - кут між віссю x$\ \vec{P}$ та β, β - кут між$\ \vec{P}$ віссю y та γ - кут між$\ \vec{P}$ віссю z.$\ \vec{P}$

Вектор положення та вектор одиниці виміру визначають площину$\ \hat{x}$, показану на лаванді нижче.$\ \vec{P}$

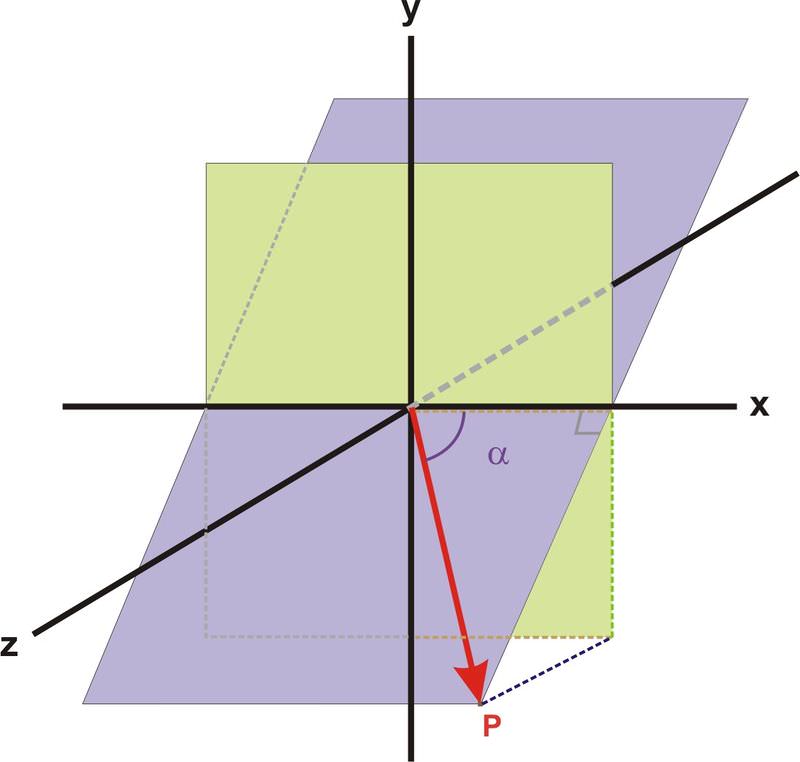
Кут напряму α - це кут між$\ \vec{P}$ і$\ \hat{x}$ в площині, який визначається двома векторами.

Інша площина, показана на схемі, - це площина XY, яка була включена в діаграму, щоб допомогти вам візуалізувати орієнтацію площини, визначеної векторами.

У нашому обговоренні точкового добутку ми побачили, що крапковий добуток двох векторів може бути заданий$\ \vec{A} \times \vec{B}=|\vec{A}||\vec{B}| \cos \theta$

Тому ми можемо обчислити кут між$\ \vec{P}$ і одиничним вектором$\ \hat{x}$.

$\ \alpha=\cos ^{-1} \frac{\vec{P} \times \hat{x}}{|\vec{P}|}$

Аналогічно кути напряму β і γ можна обчислити за допомогою рівнянь

$\ \beta=\cos ^{-1} \frac{\vec{P} \times \hat{y}}{|\vec{P}|} \text { and } \gamma=\cos ^{-1} \frac{\vec{P} \times \hat{z}}{|\vec{P}|}$

У деяких додатках, таких як астрономія та прикладна оптика, косинуси напряму використовуються принаймні так само часто, як і самі кути спрямованості.

$\ \cos \alpha=\frac{\vec{P} \times \hat{x}}{|\vec{P}|}, \cos \beta \frac{\vec{P} \times \hat{y}}{|\vec{P}|}, \text { and } \cos \gamma=\frac{\vec{P} \times \hat{z}}{|\vec{P}|}$

Піфагорійська властивість косинусів напряму

Цікаву властивість косинусів напряму можна побачити, якщо записати рівняння для косинусів напряму через складові вектора положення, P _x, P _y та P _z і використовуючи визначення величини вектора$\ |\vec{A}|=\sqrt{A_{x}^{2}+A_{y}^{2}+A_{z}^{2}}$

Наприклад,

$\ \cos \alpha=\frac{P_{x}}{\sqrt{P_{x}^{2}+P_{y}^{2}+P_{z}^{2}}}$

Інші два спрямованих косинуса можна переписати аналогічно:

$\ \cos \beta=\frac{P_{y}}{\sqrt{P_{x}^{2}+P_{y}^{2}+P_{z}^{2}}} \text { and } \cos \gamma=\frac{P_{z}}{\sqrt{P_{x}^{2}+P_{y}^{2}+P_{z}^{2}}}$

Якщо ми квадратимо обидві сторони всіх трьох рівнянь, а потім підсумовуємо їх, отримаємо

$\ \cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma=\frac{P_{x}^{2}}{P_{x}^{2}+P_{y}^{2}+P_{z}^{2}}+\frac{P_{y}^{2}}{P_{x}^{2}+P_{y}^{2}+P_{z}^{2}}+\frac{P_{z}^{2}}{P_{x}^{2}+P_{y}^{2}+P_{z}^{2}}$

що спрощує

$\ \cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma=\frac{P_{x}^{2}+P_{y}^{2}+P_{z}^{2}}{P_{x}^{2}+P_{y}^{2}+P_{z}^{2}}=1$

Це важливий результат, оскільки визначення вектора одиниці зазначено,$\ |\hat{u}|=1$ що також означає, що

$\ u_{x}^{2}+u_{y}^{2}+u_{z}^{2}=\cos ^{2} a+\cos ^{2} \beta+\cos ^{2} \gamma$

і щоб складові одиничних векторів відповідали напряму косинусів.

---

Приклади

Приклад 1

Раніше вам давали проблему про Аліссу та гру з нокдауном.

Якщо Алісса знає власну висоту кидання та відстань, яку банки укладені за лінією метання, (а) що ще їй потрібно знати, щоб обчислити вектори, пов'язані з прямою лінією шляху для м'яча? (б) Як би вона їх обчислила?

Рішення

1. Алісі потрібно знати висоту банок над землею.
2. Якщо Алісса припускає, що центр банок знаходиться безпосередньо перед нею, і розглядає власну руку як початок, вона може обчислити векторні напрямки, як зазначено вище, використовуючи 0 для x, різницю між висотою кидання та висотою банок як y, і відстань, яку банки укладають за межі лінії метання як z.

Приклад 2

Оскільки літаки рухаються у трьох вимірах, наземні екіпажі повітряних суден можуть використовувати косинуси напряму, щоб визначити своє місце розташування в будь-який момент. Замість довільного набору ортогональних осей x, y та z, положення літака вимірюється відносно східного, північного та зенітного напрямків. (Зеніт означає зверху або вгору.) У конкретний момент невеликий літак знаходиться в 297 км на схід, 135 км на північ і 7,5 км над своїм рідним аеропортом. Які спрямовані косинуси і кути спрямованості для вектора положення площини в цей момент?

Рішення

Якщо використовувати стандартну орієнтацію карт у північній півкулі, напрямок x відповідає східному, напрямку y - на північ, а z-напрямку - зеніту. Тому вектор положення площини можна записати як$\ \vec{P}=\langle 297,135,7.5\rangle \mathrm{km}$.

Напрямні косинуси, пов'язані з цим вектором, задаються

\ (\\ почати {масив} {л}
\ cos\ альфа =\ frac {\ vec {P}\ раз\ капелюх {x}} {|\ vec {P} |} =\ фракція {P_ {x}} {\ sqrt {P} ^ {2} +P_ {y} ^ {2} +P_ {z} ^ {2}}}\ cos
\ альфа =\ розрив {P_ {x}} {\ sqrt {P_ {x} ^ {2} +P_ {y} ^ {2} +P_ {z} ^ {2}} =\ frac {297} {\ sqrt {297^ {2} +135^ {2} +7.5^ {2}}}} =0.582\\ cos
\ beta=\ frac {\ vec {P}\ раз\ капелюх {у}} {|\ vec {P} |} =\ розрив {P_ {y}} {\ sqrt {P} ^ {x} ^ {2} +P_ {z} ^ {2}}}\\ cos\ beta=
\ frac {P_ {y}}} {\ sqrt {P_ {x} ^ {2}} +P_ {y} ^ {2} +P_ {z} ^ {2}}} =\ розрив {135} {\ sqrt {297^ {2} +135^ {2} +7.5^ {2}}} =0.811\\ cos
\ gamma=\ frac {\ vec {P}\ час\ капелюх {z}} {\ vec {P} |} =\ розрив {P_ {z}} {\ sqrt {P_ {x} ^ {2} +P_ {y} ^ {2 } +P_ {z} ^ {2}}}\\ cos
\ gamma=\ розрив {P_ {z}} {\ sqrt {P} ^ {x} ^ {2} +P_ {z} ^ {2}}} =\ frac {7500} {\ sqrt {297^ {2} +135^ {2} +135^ {2} 7.5^ {2}}} =0.045
\ end {масив}\)

Пов'язані кути напряму

\ (\\ почати {масив} {л}
a=\ cos ^ {-1} 0.582=54.4^ {\ circ}\
\ бета=\ cos ^ {-1} 0.165=35.8^ {\ circ}\\
y=\ cos ^ {-1} 0,045=87.4^ {\ circ}
\ кінець {масив}\)

Приклад 3

У майбутньому епізоді кримінальної драми рій комах особливого ефекту турбує одного з слідчих після виявлення жертви вбивства в дренажній канаві. Аніматор використовує вектори позицій для відстеження позицій віртуальних шкідників щодо походження на голові слідчого. Одне таке комаха розташовується в точці 33 см спереду, на 52 см зліва, і на 18 см нижче кінчика носа слідчого. Які спрямовані косинуси у цієї комахи?

Рішення

Коли ми дивимося на нашого слідчого, напрямок +x знаходиться ліворуч від неї, +y напрямок вгору від її носа, а напрямок +z знаходиться перед нею. Вектор положення мошки можна записати як$\ \vec{P}=\langle 33,52,-18\rangle \mathrm{cm}$.

Напрямні косинуси, пов'язані з цим вектором, задаються

\ (\\ почати {масив} {л}
\ cos\ альфа =\ frac {\ vec {P}\ раз\ капелюх {x}} {|\ vec {P} |} =\ фракція {P_ {x}} {\ sqrt {P} ^ {2} +P_ {y} ^ {2} +P_ {z} ^ {2}}}\ cos
\ альфа =\ розрив {P_ {x}} {\ sqrt {P_ {x} ^ {2} +Р_ {у} ^ {2} +P_ {z} ^ {2}}} =\ frac {33} {\ sqrt {33^ {2} +52^ {2} + (-18) ^ {2}}}} =0.514\\ cos
\ beta=\ гідророзриву {\ vec {P}\ раз\ капелюх {у}} {|\ vec {P} |} =\ розрив {P_ {y}} {\ sqrt {P} ^ {x} ^ {2} +P_ {z} ^ {2}}}\\ cos\ beta=
\ frac {P_ {y}}} {\ sqrt {P_ {x} ^ {2}} +P_ {y} ^ {2} +P_ {z} ^ {2}}} =\ frac {52} {\ sqrt {33^ {2} +52^ {2} + (-18) ^ {2}}} =0.810\\ cos
\ gamma=\ frac {\ vec {P}\ час\ капелюх {z}} {| | vec {P} |} =\ розрив {P_ {z}} {\ sqrt {P_ {x} ^ {2} +P_ {y} ^ {2} +P_ {z} ^ {2}}}\
\ cos\ гамма=\ frac {P_ {z}} {\ sqrt {P} ^ {x} ^ {2} +P_ {z} ^ {2}}} =\ frac {-18} {\ sqrt {33^ {2} +52^ {2} + (-18)) ^ {2}}} =-0.281
\ кінець {масив}\)

Приклад 4

Місцевий астроном використовував косинуси напряму при програмуванні проектора в новому куполі планетарію. Сам проектор сидить в центрі купола, 2,5 м над підлогою. Він бажає спроектувати Мінтаку, одну із зірок у поясі Оріона, на позиції 12 м на південь та 2,3 м на схід від проектора та 8,7 м над підлогою. Яке рівняння спрямованого одиничного вектора, яке астроном повинен ввести в проекційний комп'ютер?

Рішення

Ми можемо використовувати ту саму систему координат, яку ми використовували в прикладі A вище:$\ \hat{x}=\text { east }$$\ \hat{y}=\text { north }$,, і$\ \hat{z}=\text { upward }$. Сам проектор - це походження. У такій системі координат стає вектор положення для Mintaka$\ \vec{P}=\langle 2.3,-12,(8.7-2.5)\rangle=\langle 2.3,-12,6.2\rangle$. Зверніть увагу, що ми не використовували положення Mintaka над підлогою як z-координату. Швидше, оскільки проектор знаходиться на 2,5 м над підлогою, нам потрібно було використовувати різницю між висотою стелі та висотою проектора. Використовуйте складову форму рівняння спрямованого косинуса для обчислення трьох компонентів одиничного вектора.

\ (\\ почати {масив} {л}
\ cos\ альфа =\ розрив {P_ {x}} {\ sqrt {P_ {x} ^ {2} +P_ {y} ^ {2}} +Р_ {2}}} =\ frac {2.3} {\ sqrt {2.3^ {2} + (-12) ^ {2} ^ {2} ^ {2} +6.2^ {2}}} =0.168\
\ cos\ beta=\ розрив {P_ {x}} {\ sqrt {P_ {x} ^ {2} +P_ {y} ^ {z} ^ {2}}} =\ frac {-12} {\ sqrt {2.3^ {2} + (-12) ^ {2} ^ {2} ^ {2} ^ {2} ^ {2} 2}}} =-0.876\
\ cos\ гамма=\ розрив {P_ {x}} {\ sqrt {P_ {x} ^ {2} +P_ {y} ^ {y} ^ {z} ^ {2}} =\ frac {6.2} {\ sqrt {2.3^ {2} + (-12) ^ {2} +6.2^ {2}}}} =0.453
\ кінець {масив}\)

Тому вектор одиниці положення задається за допомогою$\ \hat{u}=\langle 0.168,-0.876,0.453\rangle$.

Приклад 5

Визначте складові вектора положення,$\ \vec{P}=\langle 2.4,5.3,1.8\rangle$ потім визначте спрямовані кути між цим вектором і віссю x.

Рішення

\ (\\ почати {масив} {л}
\ cos\ альфа =\ frac {\ vec {P}\ раз\ капелюх {x}} {|\ vec {P} |} =\ фракція {P_ {x}} {\ sqrt {P} ^ {2} +P_ {y} ^ {2} +P_ {z} ^ {2}}}\ cos
\ альфа =\ frac {\ vec {P}\ раз\ hat {x}} {|\ vec {P} |} =\ frac {2.4} {\ sqrt {(2.4) ^ {2} + (5.3) ^ {2}}} =\ frac {2.4} {\ sqrt {5.76+28.09+3.24}} =\ frac {2.4} {\ sqrt {37 .09}} =0.394\\
альфа=\ cos ^ {-1} 0,394=66.8
\ кінець {масив}\)

Приклад 6

Визначте напрямок косинусів для вектора$\ \vec{N}=\langle 8,3,-5\rangle$.

Рішення

\ (\\ почати {вирівняні}
&\ cos\ альфа =\ frac {\ vec {N}\ раз\ капелюх {x}} {|\ vec {N} |} =\ frac {N_ {x}} {\ sqrt {N} ^ {2} +N_ {y} ^ {2} +N_ {z} ^ {2}}}\
&\ cos\ альфа =\ frac {\ vec {N}\ раз\ капелюх {x}} {|\ vec {N} |} =\ frac {N_ {x}} {\ sqrt {x} ^ {2} +N_ {z} ^ {2}}} =\ frac {8} {\ sqrt {(8) ^ {2} + (3) ^ {2} + (-5) ^ {2}}} =\ Фрак {8} {\ sqrt {64+9+25}} =0.7213\\
&\ cos\ beta=\ frac {\ vec {N}\ раз\ hat {y}} {|\ vec {N} |} =\ frac {N_ {y}} {\ sqrt {N} ^ {2} +N_ {y} ^ {2} +N_ {y} ^ {2} {z} ^ {2}}}\\
&\ cos\ beta=\ frac {\ vec {N}\ раз\ капелюх {y}} {|\ vec {N} |} =\ frac {N_ {y}}

UndefinedNameError: reference to undefined name 'y' (click for details)

Callstack:
    at (Доколеджна_освіта/Математика/Аналіз/05:_Векторний_аналіз/5.03:_Літаки_в_космосі/5.3.02:_Векторний_напрямок), /content/body/div[3]/div[6]/div/p[3]/span, line 1, column 1

{N} ^ {y} ^ {2} +N_ {z} ^ {z} ^ {2}}} c {3} {\ sqrt {(8) ^ {2} + (3) ^ {2} + (- 5) ^ {2}}} =\ frac {3} {\ sqrt {64+9+25}} =0.3030\
&\ cos\ гамма =\ frac {\ vec {N}\ раз\ капелюх {z}} {|\ vec {N} |} =\ frac {N_ {z}} {\ sqrt {N_ {x} ^ {2} +N_ {y} ^ {2} +N_ {z} ^ {2}}}\\
&\ cos\ gamma=\ frac {\ vec {N}\ раз\ капелюх {z}} {|\ vec {N} |} =\ frac {N_ {z}} {\ sqrt {N_ {x} ^ {2} +N_ {y} ^ {Z} ^ {Z}} ^ {2}}} =\ frac {-5} {\ sqrt {(8) ^ { 2} + (3) ^ {2} + (-5) ^ {2}}} =\ розрив {-5} {\ sqrt {64+9+25}} =-0.5051
\ кінець {вирівняний}\)

Приклад 7

Визначте вектор положення для невеликого літака на даний момент це 2,5 км на схід, 8,8 км на південь і 4,1 км над його рідним аеропортом. Використовуйте систему координат, де напрямок x відповідає східному напрямку, напрямку y на північ та z-напрямку до зеніту. Потім визначте спрямовані косинуси, які використовуються персоналом управління повітряним рухом для ідентифікації місця розташування літака.

Рішення

У цій системі координат, з початком у домашньому аеропорту, вектор положення задається$\ \vec{r}=\langle 2.5,-8.8,4.1\rangle$ одиницями кілометрів.

\ (\\ почати {масив} {л}
\ cos\ альфа =\ frac {\ vec {r}\ раз\ капелюх {x}} {|\ vec {r} |} =\ frac {r_ {x}} {\ sqrt {x} ^ {2} +r_ {y} ^ {2} +r_ {z} ^ {2}}}
\ cos\ альфа =\ розрив {\ vec {r}\ раз\ капелюх {x}} {|\ vec {r} |} =\ frac {r_ {x}} {\ sqrt {x} ^ {2} +r_ {z} ^ {2}}} =\ frac {2.5} {\ sqrt (2.5) ^ {2} ^ {2} + (-8.8) ^ {2} + (4.1) ^ {2}}} =\ фракція {2.5} {\ sqrt {100.5}} =0.249\
\ cos\ beta=\ фракція {\ vec {r}\ час {y}} {|\ vec {r} |} =\ frac {r_ {y}} {\ sqrt {r_ {x} ^ {2} +r_ {y} ^ {2} +r_ {y} ^ {2} +r_ {2} +r_ {z} 2}}}\\ cos\ бета=\ фракція {\ vec {r}\ раз\ шат {y}} {|\ vec {r} |} =\ frac {r_ {y}} {\ sqrt {r_ {x} ^ {2} +r_ {y} ^ {2} +r_ {z} ^ {2}}} =\ frac {-8.8}\ sqrt {(2.5) ^ {2} + (-8.8) ^ {2} + (4.
1) ^ {2}}} =\ frac {-8.8} {\ sqrt {100.5}} =-0,878\
\ cos\ gamma=\ frac {\ vec {r}\ час\ hat {z}} {|\ vec {r} |} =\ frac {r_z} {\ sqrt {r_ {x} ^ {2} +r_ {y} ^ {y} 2} +r_ {z} ^ {2}}}\\ cos
\ gamma=\ фракція {\ vec {r}\ раз\ капелюх {z}} {|\ vec {r} |} =\ frac {r_z} {\ sqrt {r_ {x} ^ {2} +r_ {y} ^ {2} +r_ {z} ^ {2} +r_ {z} ^ {2}}\ frac {4.1} {\ sqrt {(2.5) ^ {2} + (-8.8 ) ^ {2} + (4.1) ^ {2}}} =\ frac {4.1} {\ sqrt {100.5}} =0.409
\ кінець {масив}\)

Приклад 8

Використовувати метод косинусів напряму для ідентифікації вектора одиниці, що має той самий напрямок, що і вектор положення$\ \vec{R}=\langle 791,978,1310\rangle$

Рішення

Вектор одиниці, який має той самий напрямок, що і цей вектор, має компоненти$\ \hat{u}=\langle\cos \alpha, \cos \beta, \cos \gamma\rangle$, де

\ (\\ почати {масив} {л}
\ cos\ альфа =\ фракція {\ vec {R}\ раз\ капелюх {x}} {|\ vec {R} |} =\ frac {R_ {x}} {\ sqrt {R} ^ {x} ^ {2} +R_ {y} ^ {2} +R_ {z} ^ {2}}},\ cos\ beta=\ розрив {\ vec {R}\ раз\ hat {y}} {|\ vec {R} |} =\ розрив {R_ {y}} {\ sqrt {R_ {x} ^ {2} +R_ {z} ^ {2}}},\ текст {і}\\ cos
\ gamma=\ frac {\ vec {R}\ раз\ капелюх {z}} {|\ vec {R} |} =\ розрив {R_ {z}} {\ sqrt {R_ {x} ^ {2} +R_ {y} ^ {2} +R_ {z} ^ {2}}}
\ кінець {масив}\)

Як тільки ми знайдемо три напрямки косинусів, у нас є компоненти вектора одиниці,

\ (\\ почати {масив} {l}
\ cos\ альфа =\ frac {\ vec {R}\ раз\ капелюх {x}} {|\ vec {R} |} =\ frac {791} {\ sqrt {791^ {2} +978^ {2}} +1310^ {2}}}} =\ frac {791} {\ sqrt {329826}}} =\ розрив {791} {1816.11} =0.436\
\ cos\ beta=\ frac {\ vec {R}\ час\ капелюх {y}} {|\ vec {R} |} =\ frac {978} {\ sqrt {791^ {2} +978^ {2} +1310^ {2}}} =\ frac {978} 78} {\ sqrt {3298265}} =\ frac {978} {1816.11} =0.539\
\ cos\ gamma=\ frac {\ vec {R}\ раз\ капелюх {z}} {|\ vec {R} |} =\ frac {1310} {\ sqrt {791^ {2} +978^ {2} +1310^ {2} =\ frac {1310} {\ sqrt {3298265}} =\ frac {1310} {1816.11} = 0.721\\
hat {u} =\ лангле\ cos\ альфа,\ cos\ бета,\ cos\ гамма\ діапазон=\ лангл 0.436,0.539,0.721 \ діапазон
\ end {масив}\)

Приклад 9

Визначте кути напряму між вектором$\ \vec{p}=\langle 25,8,15\rangle$ і осями координат.

Рішення

\ (\\ почати {масив} {л}
\ cos\ альфа =\ frac {\ vec {P}\ раз\ капелюх {x}} {|\ vec {P} |} =\ фракція {P_ {x}} {\ sqrt {P} ^ {2} +P_ {y} ^ {2} +P_ {z} ^ {2}}}\ cos
\ альфа =\ frac {\ vec {P}\ раз\ hat {x}} {|\ vec {P} |} =\ frac {25} {\ sqrt {(25) ^ {2} + (8) ^ {2} + (15) ^ {2}}} =\ frac {25} {\ sqrt {914}}} =\ frac {25} =0.827\\
\ альфа =\ cos ^ {-1} 0.827=34.2^ {\ circ}\
\ cos\ beta=\ frac {\ vec {P}\ раз\ капелюх {y}} {|\ vec {P} |} =\ frac {P_ {y}} {\ sqrt {P} ^ {2} +P_ {y} ^ {2} +P_ {y} ^ {2} z} ^ {2}}}\
\ cos\ beta=\ frac {\ vec {P}\ раз\ капелюх {y}} {|\ vec {P} |} =\ frac {8} {\ sqrt {(25) ^ {2} + (8) ^ {2} + (15) ^ {2}}} =\ frac {8} {\ sqrt {914}} =\ фрейк {8} {30.23} =0 .265\
\\ бета=\ cos ^ {-1} 0.265=75.7^ {\ circ}\
\ cos\ gamma=\ frac {\ vec {P}\ раз\ капелюх {z}} {|\ vec {P} |} =\ frac {P_ {z}} {\ sqrt {P_ {x} ^ {2} +P_ {y} ^ {y} 2} +P_ {z} ^ {2}}}
\\ cos\ gamma=\ frac {\ vec {P}\ раз\ капелюх {z}} {|\ vec {P} |} =\ frac {15} {(25) ^ {2} + (8) ^ {2} + (15) ^ {2}}} =\ frac {15} {15}} квадратний { 914}} =\ гідророзриву {15} {30.23} =0.496\
\ гамма=\ cos ^ {-1} 0,496=60.25^ {\ circ}
\ кінець {масив}\)

---

Рецензія

Який напрямок вектора в градусах наступних двовимірних векторів, припускаючи, що позитивна вісь x дорівнює 0 ^o?

1. Що таке напрямок$\ \langle-4,8\rangle$
2. Що таке напрямок$\ \langle-9,20\rangle$
3. Що таке напрямок$\ \langle 9,20\rangle$
4. Що таке напрямок$\ \langle 2,18\rangle$
5. Що таке напрямок$\ \langle 7,5\rangle$
6. Що таке напрямок$\ \langle 9,16\rangle$

Визначте напрямки косинусів, пов'язаних із заданим вектором.

7. $\ \vec{P}=\langle 42,6,9.5\rangle$а) cos α = б) cos β = в) cos γ =
8. $\ \vec{P}=\langle 50,70,40.25\rangle$а) cos α = б) cos β = в) cos γ =
9. $\ \vec{P}=\langle 75,30,102\rangle$а) cos α = б) cos β = в) cos γ =
10. $\ \vec{P}=\langle 145,130,25.75\rangle$а) cos α = б) cos β = в) cos γ =
11. $\ \vec{P}=\langle 220,300,175\rangle$а) cos α = б) cos β = в) cos γ =

Визначте кути напряму між заданим вектором і осями координат.

12. $\ \vec{P}=\langle 13,30,17\rangle$
13. $\ \vec{P}=\langle 5,3,12\rangle$
14. $\ \vec{P}=\langle 75,130,45\rangle$
15. $\ \vec{P}=\langle 90,30,60\rangle$
16. $\ \vec{P}=\langle 7,18,4\rangle$

Вирішіть завдання слів, як зазначено.

17. Визначте вектор положення для повітряного змія в той момент, коли він становить 3,5 м на схід, 10,8 м на південь і 30 м над дитиною, що летить на ньому. Використовуйте систему координат, де напрямок x відповідає східному напрямку, напрямку y на північ та z-напрямку до зеніту. Потім визначте спрямовані косинуси, щоб визначити розташування повітряних зміїв.
18. Визначте вектор положення кота, що застряг у дереві на даний момент, він знаходиться на 7 футів на схід, 12,3 футів на південь і 25 футів над основою дерева. Використовуйте систему координат, де напрямок x відповідає східному напрямку, напрямку y на північ та z-напрямку до зеніту. Потім визначте спрямовані косинуси, щоб визначити місце розташування кішок.

---

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 5.9.

---

Лексика

Термін	Визначення
кутові косинуси	Кутові позначення або кутові косинуси описують вектор як результат окремих величин і напрямків, виміряних від осей, починаючи від початку.
позначення кута	Кутові позначення або кутові косинуси описують вектор як результат окремих величин і напрямків, виміряних від осей, починаючи від початку.
Компонентні позначення	Компонентні позначення використовуються для опису векторів алгебраїчно через їх x, y та, якщо це доречно, z компонентів.
кути напряму	Кути напряму (також відомі як косинуси напряму) описують вектор як результат окремих величин і напрямків, виміряних від осей, починаючи від початку.
косинуси напряму	Напрямні косинуси (також відомі як кути напряму) описують вектор як результат окремих величин і напрямків, виміряних від осей, починаючи від початку.
точковий добуток	Точковий добуток також відомий як внутрішній продукт або скалярний продукт. Дві форми точкового добутку є$\ \vec{a} \cdot \vec{b}=\|\vec{a}\|\|\vec{b}\| \cos \theta \text { and } \vec{a} \cdot \vec{b}=x_{a} x_{b}+y_{a} y_{b}$.
вектор положення	Вектор положення описує пряму лінію між початковою точкою (зазвичай початковою точкою) і розташуванням другої точки на координатній площині.
одиниця вектор	Одиничний вектор - це вектор з величиною одиниці.