12.2: Представлення машин Тьюринга

Template:MathJaxZach

Машини Тьюринга можуть бути представлені візуально діаграмами стану. Діаграми складаються з комірок стану, з'єднаних стрілками. Не дивно, що кожна державна клітина являє собою стан машини. Кожна стрілка являє собою інструкцію, яку можна виконувати з того стану, зі специфікою інструкції, написаної вище або під відповідною стрілкою. Розглянемо наступну машину, яка має всього два внутрішніх стану,\(q_0\) і\(q_1\), і одну інструкцію:

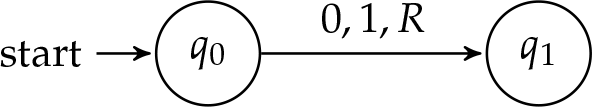
Нагадаємо, що машина Тьюринга має головку читання/запису і стрічку з написаним на ній входом. Інструкцію можна прочитати так, ніби читаючи\(\TMblank\) в стані\(q_0\), написати\(\TMstroke\), рухатися вправо і перейти до стану\(q_1\). Це еквівалентно відображенню функції переходу\(\tuple{q_0, \TMblank}\) до\(\tuple{q_1, \TMstroke, \TMright}\).

Приклад\(\PageIndex{1}\)

Навіть машина: Наступна машина Тьюринга зупиняється, якщо, і тільки якщо, на стрічці є\(\TMstroke\) парне число (за припущенням, що все\(\TMstroke\) прийшло до першого\(\TMblank\) на стрічці).

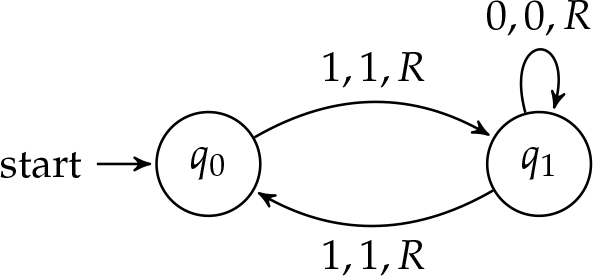
Діаграма стану відповідає наступна функція переходу:

\[\begin{aligned} \delta(q_0, \TMstroke) & = \tuple{q_1, \TMstroke, \TMright},\\ \delta(q_1, \TMstroke) & = \tuple{q_0, \TMstroke, \TMright},\\ \delta(q_1, \TMblank) & = \tuple{q_1, \TMblank, \TMright}\end{aligned}\]

Вищевказана машина зупиняється тільки тоді, коли на вході йде парна кількість ударів. В іншому випадку машина (теоретично) продовжує працювати нескінченно довго. Для будь-якої машини та входу можна простежити конфігурації машини, щоб визначити вихід. Формальне визначення конфігурацій ми дамо пізніше. Наразі ми можемо інтуїтивно думати про конфігурації як ряд діаграм, що показують стан машини в будь-який момент часу під час роботи. Конфігурації показують вміст стрічки, стан машини і розташування головки читання/запису.

Давайте простежимо конфігурації парної машини, якщо вона запущена з входом чотирьох\(\TMstroke\), в цьому випадку ми очікуємо, що машина зупиниться. Потім ми будемо запускати машину на вході трьох\(\TMstroke\), де машина буде працювати назавжди.

Машина запускається в стані\(q_0\), скануючи крайній лівий\(\TMstroke\). Ми можемо представити початковий стан машини наступним чином:\[\TMendtape \TMstroke_0 \TMstroke \TMstroke \TMstroke \TMblank \ldots\nonumber\] Наведена вище конфігурація проста. Як видно, машина запускається в стані один, скануючи крайній лівий\(\TMstroke\). Це представлено індексом назви держави на першому\(\TMstroke\). Застосовувана інструкція в цей момент є\(\delta(q_0, \TMstroke) = \tuple{q_1, \TMstroke, \TMright}\), і тому машина рухається прямо по стрічці і переходить в стан\(q_1\). \[\TMendtape \TMstroke \TMstroke_1 \TMstroke \TMstroke \TMblank \ldots\nonumber\]Оскільки машина зараз знаходиться в стані\(q_1\) сканування a\(\TMstroke\), ми повинні «слідувати» інструкції\(\delta(q_1, \TMstroke) = \tuple{q_0, \TMstroke, \TMright}\). Це призводить до конфігурації\[\TMendtape \TMstroke \TMstroke \TMstroke_0 \TMstroke \TMblank \ldots\nonumber\] Як машина продовжує, правила застосовуються знову в тому ж порядку, в результаті чого наступні дві\[\TMendtape \TMstroke \TMstroke \TMstroke \TMstroke_1 \TMblank \ldots\nonumber\]\[\TMendtape \TMstroke \TMstroke \TMstroke \TMstroke \TMblank_0 \ldots\nonumber\] конфігурації: машина в даний час в стані\(q_0\) сканування \(\TMblank\). Виходячи з схеми переходу, ми можемо легко побачити, що немає інструкції, яку потрібно виконувати, і таким чином машина зупинилася. Це означає, що вхід прийнятий.

Припустимо, далі ми запускаємо автомат з входом\(\TMstroke\) трьох. перші кілька конфігурацій аналогічні, так як виконуються ті ж інструкції, з лише невеликою різницею стрічкового введення:\[\TMendtape \TMstroke_0 \TMstroke \TMstroke \TMblank \ldots\nonumber\]\[\TMendtape \TMstroke \TMstroke_1 \TMstroke \TMblank \ldots\nonumber\]\[\TMendtape \TMstroke \TMstroke \TMstroke_0 \TMblank \ldots\nonumber\]\[\TMendtape \TMstroke \TMstroke \TMstroke \TMblank_1 \ldots\nonumber\] Машина тепер пройшла повз усіх\(\TMstroke\), і читає\(\TMblank\) в стані\(q_1\). Як показано на схемі, є інструкція бланка\(\delta(q_1, \TMblank) =\tuple{q_1, \TMblank, \TMright}\). Так як стрічка заповнена на\(\TMblank\) невизначений термін праворуч, машина буде продовжувати виконувати цю інструкцію назавжди, залишаючись в стані\(q_1\) і рухаючись все далі вправо. Машина ніколи не зупиниться, і не приймає вхід.

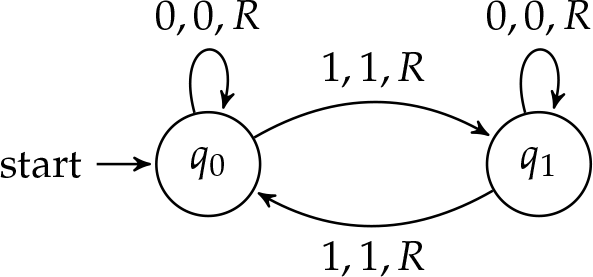
Важливо відзначити, що не всі машини зупиняться. Якщо зупинка означає, що машина закінчується інструкціями для виконання, то ми можемо створити машину, яка ніколи не зупиняється, просто гарантуючи, що є вихідна стрілка для кожного символу в кожному стані. Навіть машина може бути змінена для роботи на невизначений час, додавши інструкцію для сканування\(\TMblank\) at\(q_0\).

Приклад\(\PageIndex{2}\)

Машинні столи - ще один спосіб представлення машин Тьюринга. Таблиці машин мають стрічковий алфавіт, що відображається на\(x\) -осі, і набір станів машини поперек\(y\) -осі. Усередині таблиці, на перетині кожного стану та символу, написана решта інструкції - новий стан, новий символ та напрямок руху. Таблиці верстатів дозволяють легко визначити, в якому стані, і за яким символом машина зупиняється. Всякий раз, коли в таблиці є розрив, можлива точка для зупинки машини. На відміну від діаграм стану і наборів інструкцій, де точки, в яких зупиняється машина, не завжди відразу очевидні, будь-які точки зупинки швидко виявляються шляхом знаходження зазорів в таблиці верстата.

Приклад\(\PageIndex{3}\)

Стіл верстата для парної машини - це:

\ [\ begin {масив} {|c|c|c|c|}
\ hline
&\ tmБланк &\ tmОбведення &\ tmОбведення\\\ hline
q_0 &\ tmTrans {
\ TMStroke} {\ tmRight} {\ tmRight}\\ hline
q_1 &\ ТМТранс {\ TMБланк} {q_1} {\ tmRight}
&\ TMTrans {\ tMStroke} {q_0} {\ tMRight} &
\ фантом {\ TMTrans {\ tmStroke} {q_1} {\ tmRight}}\\ hline
\ кінець {масив}\ nonnumber\]

Як ми бачимо, машина зупиняється при скануванні заготовки в стані\(q_0\).

Поки ми розглядали лише машини, які читають та приймають введення. Однак машини Тьюринга мають здатність як читати, так і писати. Прикладом такої машини (хоча існує багато-багато прикладів) є дублер. Дублер, коли він запускається з\(n\)\(\TMstroke\) блоком з на стрічці, виводить блок з\(2n\)\(\TMstroke\).

Приклад\(\PageIndex{4}\)

Перш ніж будувати машину дублер, важливо придумати стратегію вирішення проблеми. Оскільки машина (як ми її сформулювали) не може згадати, скільки\(\TMstroke\) вона прочитала, нам потрібно придумати спосіб відстежувати всі на\(\TMstroke\) стрічці. Одним з таких способів є відокремлення виходу від входу за допомогою a\(\TMblank\). Потім машина може стерти перший\(\TMstroke\) з вхідних даних, перейти на решту вхідних даних, залишити і написати два нових\(\TMblank\)\(\TMstroke\), Потім машина повернеться назад і знайде другий на\(\TMstroke\) вході, а також подвоїти цей. Для кожного з\(\TMstroke\) вхідних даних, він\(\TMstroke\) запише два з виводу. Стираючи вхід, коли машина йде, ми можемо гарантувати, що ні\(\TMstroke\) пропущено або подвоюється двічі. Коли весь вхід буде стертий, на стрічці залишиться\(2n\)\(\TMstroke\) 's. Діаграма стану отриманої машини Тьюринга зображена на малюнку\(\PageIndex{1}\).

Малюнок\(\PageIndex{1}\): Подвійний верстат

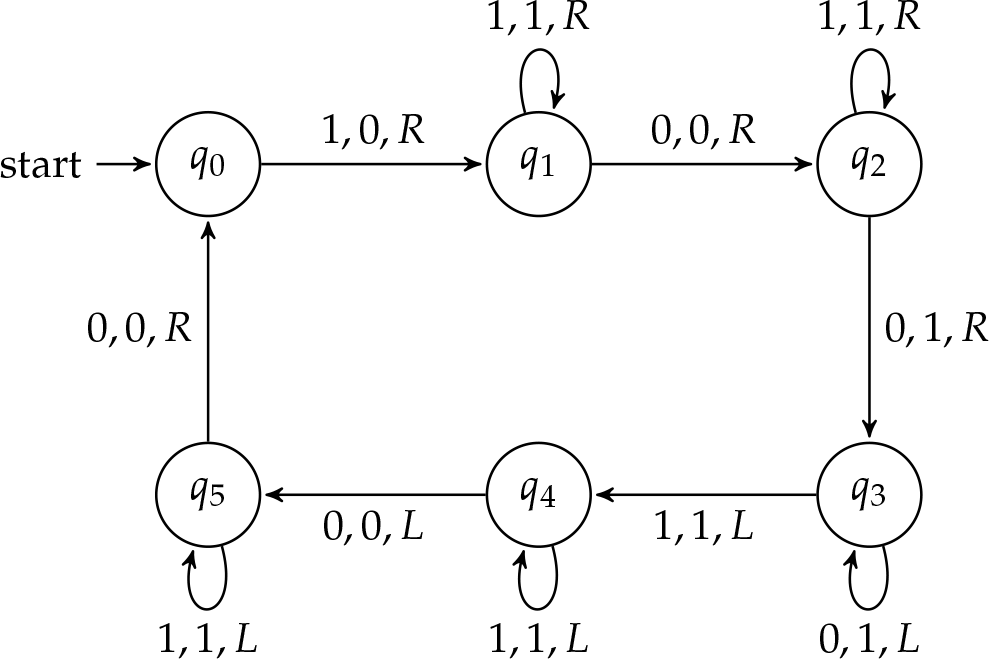
Проблема\(\PageIndex{1}\)

Choose an arbitary input and trace through the configurations of the doubler machine in Example \(\PageIndex{4}\).

Problem \(\PageIndex{2}\)

The double machine in Example \(\PageIndex{4}\) writes its output to the right of the input. Come up with a new method for solving the doubler problem which generates its output immediately to the right of the end-of-tape marker. Build a machine that executes your method. Check that your machine works by tracing through the configurations.

Problem \(\PageIndex{3}\)

Design a Turing-machine with alphabet \(\{\TMendtape,\TMblank, A, B\}\) that accepts, i.e., halts on, any string of \(A\)’s and \(B\)’s where the number of \(A\)’s is the same as the number of \(B\)’s and all the \(A\)’s precede all the \(B\)’s, and rejects, i.e., does not halt on, any string where the number of \(A\)’s is not equal to the number of \(B\)’s or the \(A\)’s do not precede all the \(B\)’s. (E.g., the machine should accept \(AABB\), and \(AAABBB\), but reject both \(AAB\) and \(AABBAABB\).)

Problem \(\PageIndex{4}\)

Design a Turing-machine with alphabet \(\{\TMendtape,\TMblank, A, B\}\) that takes as input any string \(\alpha\) of \(A\)’s and \(B\)’s and duplicates them to produce an output of the form \(\alpha\alpha\). (E.g. input \(ABBA\) should result in output \(ABBAABBA\)).

Problem \(\PageIndex{5}\)

Alphabetical?: Design a Turing-machine with alphabet \(\{\TMendtape,\TMblank, A, B\}\) that when given as input a finite sequence of \(A\)’s and \(B\)’s checks to see if all the \(A\)’s appear to the left of all the \(B\)’s or not. The machine should leave the input string on the tape, and either halt if the string is “alphabetical”, or loop forever if the string is not.

Problem \(\PageIndex{6}\)

Alphabetizer: Design a Turing-machine with alphabet \(\{\TMendtape,\TMblank, A, B\}\) that takes as input a finite sequence of \(A\)’s and \(B\)’s rearranges them so that all the \(A\)’s are to the left of all the \(B\)’s. (e.g., the sequence \(BABAA\) should become the sequence \(AAABB\), and the sequence \(ABBABB\) should become the sequence \(AABBBB\)).