12.1: Вступ

Last updated
Save as PDF

Page ID: 52960

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Template:MathJaxZach

Що це означає для функції, скажімо, від\(\Nat\)\(\Nat\) до бути обчислюваною? Серед перших відповідей, і найвідоміший, полягає в тому, що функція обчислюється, якщо її можна обчислити машиною Тьюринга. Це поняття було викладено Аланом Тьюрингом в 1936 році. Машини Тьюринга є прикладом моделі обчислень - вони є математично точним способом визначення ідеї «обчислювальної процедури». Що саме це означає, обговорюється, але широко прийнято вважати, що машини Тьюринга є одним із способів визначення обчислювальних процедур. Незважаючи на те, що термін «машина Тьюринга» викликає образ фізичної машини з рухомими частинами, строго кажучи, машина Тьюринга є чисто математичною конструкцією, і як така вона ідеалізує ідею обчислювальної процедури. Наприклад, ми не встановлюємо жодних обмежень ні на час, ні вимоги до пам'яті машини Тьюринга: машини Тьюринга можуть щось обчислити, навіть якщо обчислення потребують більше місця для зберігання або більше кроків, ніж атоми у Всесвіті.

Мабуть, найкраще думати про машину Тьюринга як про програму для особливого виду уявного механізму. Цей механізм складається з стрічки і головки читання-запису. У нашій версії машин Тьюринга стрічка нескінченна в одну сторону (праворуч), і вона розділена на квадрати, кожен з яких може містити символ з кінцевого алфавіту. Такі алфавіти можуть містити будь-яку кількість різних символів, скажімо, але ми в основному зробимо це з трьома:\(\TMendtape\),\(\TMblank\), і\(\TMstroke\). Коли механізм запущений, стрічка порожня (тобто кожен квадрат містить символ\(\TMblank\)), за винятком крайнього лівого квадрата, який містить\(\TMendtape\), та кінцевої кількості квадратів, які містять вхідні дані. У будь-який момент механізм знаходиться в одному з кінцевого числа станів. На самому початку голова сканує крайній лівий квадрат і в заданому початковому стані. На кожному кроці запуску механізму вміст квадрата, який зараз сканується разом із станом, в якому знаходиться механізм, і програма машини Тьюринга визначає, що буде далі. Програма машини Тьюринга задається частковою функцією, яка приймає як вхід стан\(q\) і символ\(\sigma\) і виводить потрійний\(\tuple{q', \sigma', D}\). Всякий раз, коли механізм знаходиться в стані\(q\) і читає символ\(\sigma\), він замінює символ на поточному квадраті з\(\sigma'\), голова рухається вліво, вправо або залишається поставленим відповідно до того, чи\(D\) є\(\TMleft\), \(\TMright\), або\(\TMstay\), і механізм переходить в стан\(q'\).

Наприклад, розглянемо ситуацію на рис\(\PageIndex{1}\).

**Малюнок\(\PageIndex{1}\):** Машина Тьюринга, що виконує свою програму.

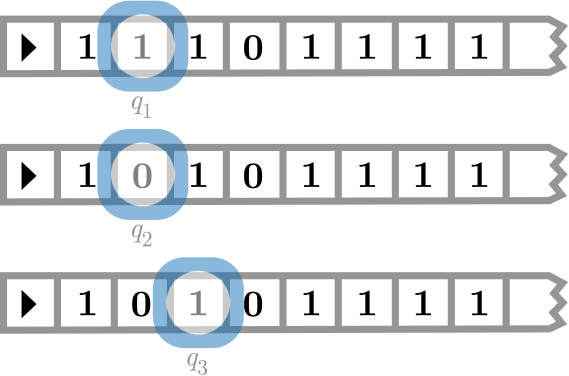
Видима частина стрічки машини Тьюринга містить символ кінця стрічки\(\TMendtape\) на крайньому лівому квадраті, а потім три\(1\)\(0\), а й ще\(1\) чотири. Голова зчитує третій квадрат зліва, який містить \(1\), і знаходиться в стані\(q_1\) —ми говоримо «машина читає\(1\) в стані»\(q_1\). Якщо програма машини Тьюринга повертає, для введення потрійний\(\tuple{q_1, 1}\)\(\tuple{q_2, 0, \TMstay}\), машина тепер замінить на третьому квадраті\(1\) на a\(0\), залиште голівку читання/запису там, де вона є, і переключиться в стан \(q_2\). Якщо тоді програма повернеться\(\tuple{q_3, 0, \TMright}\) для введення\(\tuple{q_2, 0}\), машина тепер перезапише її іншим\(0\) (фактично, залишивши вміст стрічки під головою читання/запису без змін), перемістіть один квадрат вправо, і\(0\) введіть стан\(q_3\). І так далі.

Ми говоримо, що машина зупиняється, коли він стикається з якимось станом\(q_n\), і символ,\(\sigma\) такий, що немає інструкції для\(\tuple{q_n, \sigma}\), тобто функція переходу для введення не\(\tuple{q_n,\sigma}\) визначена. Іншими словами, машина не має інструкції виконувати, і в цей момент вона припиняє роботу. Зупинка іноді представлена певним станом зупинки\(h\). Це буде продемонстровано більш детально далі.

Краса роботи Тьюринга «Про обчислювані числа» полягає в тому, що він представляє не тільки формальне визначення, але й аргумент, що визначення захоплює інтуїтивне поняття обчислюваності. З визначення повинно бути зрозуміло, що будь-яка функція, обчислювана машиною Тьюринга, обчислюється в інтуїтивному сенсі. Тьюринг пропонує три типи аргументів, що зворотне вірно, тобто, що будь-яка функція, яку ми, природно, вважаємо обчислювальною, обчислюється такою машиною. Вони є (за словами Тьюринга):

Пряме звернення до інтуїції.
Доказ еквівалентності двох визначень (у випадку, якщо нове визначення має більшу інтуїтивну привабливість).
Наведено приклади великих класів чисел, які можна обчислити.

Наша мета - спробувати визначити поняття обчислюваності «в принципі», тобто без урахування практичних обмежень часу і простору. Звичайно, з найширшим визначенням обчислюваності на місці, можна продовжувати розглядати обчислення з обмеженими ресурсами; це формує серце предмета, відомого як «обчислювальна складність».

Історичні зауваження

Алан Тьюринг винайшов машини Тьюринга в 1936 Хоча його інтерес в той час був вирішуваність логіки першого порядку, документ був описаний як остаточний документ про основи комп'ютерного дизайну. У роботі Тьюринг фокусується на обчислюваних дійсних числах, тобто дійсних числах, десяткові розширення яких обчислюються; але він зазначає, що його поняття не важко адаптувати до обчислювальних функцій на натуральних числах тощо. Зверніть увагу, що це було цілих п'ять років до того, як перший робочий комп'ютер загального призначення був побудований в 1941 році (німець Конрад Зузе у вітальні його батьків), за сім років до того, як Тьюринг та його колеги з Блетчлі-парку побудували колос, що руйнує код (1943), за дев'ять років до американського ENIAC (1945), за дванадцять років до того, як перший британський комп'ютер загального призначення - Манчестерська маломасштабна експериментальна машина - була побудована в Манчестері (1948), а за тринадцять років до того, як американці вперше випробували BINAC (1949). Манчестерський SSEM має відмінність бути першим збереженим програмним комп'ютером - попередні машини повинні були бути перероблені вручну для кожного нового завдання.