4.4: Байєсівський підхід до еволюційних темпів
Нарешті, ми також можемо використовувати байєсівський підхід, щоб пристосувати броунівські моделі руху до даних та оцінити швидкість еволюції. Цей підхід відрізняється від підходу ML тим, що ми будемо використовувати явні priors для значень параметрів, а потім запустити MCMC для оцінки задніх розподілів оцінок параметрів. Для цього ми змінимо основний алгоритм Байєсівського MCMC (див. Розділ 2) наступним чином:
- Приклад множини значень початкових параметрів σ 2 та $\ bar {z} (0) $ з їх попередніх розподілів. Для цього прикладу ми можемо встановити наш попередній розподіл як рівномірний між 0 і 0,5 для σ 2 і рівномірний від 0 до 10 для $\ bar {z} (0) $.
- Враховуючи поточні значення параметрів, виберіть нові запропоновані значення параметрів за допомогою густини пропозиції Q (p ′| p). Для обох значень параметрів ми будемо використовувати рівномірну щільність пропозиції з шириною w p, так що: (ур. 4.10)
Q(p′|p)∼U(p−wp2,p+wp2)
- Обчисліть три співвідношення:
- Коефіцієнт попереднього коефіцієнта, R p r i o r. Це відношення ймовірності витягування значень параметрів p і p 'від попереднього. Оскільки наші пріори рівномірні, це завжди 1.
- Пропозиція коефіцієнт щільності, R p r o p o s a l. Це співвідношення ймовірності пропозицій, що йдуть від p до p 'і зворотного. Ми вже оголосили симетричну щільність пропозиції, так що Q (p ′| p) = Q (p | p ′) і R p r o p o s a л = 1.
- Коефіцієнт ймовірності, R l i k e l i h o o d. Це співвідношення ймовірностей даних з урахуванням двох різних значень параметрів. Ми можемо обчислити ці ймовірності з рівняння 4.5 вище. (ур. 4,11)
Rlikelihood=L(p′|D)L(p|D)=P(D|p′)P(D|p)
- Знайдіть коефіцієнт прийняття, R a c c e p t, який є добутком попередніх коефіцієнтів, коефіцієнта щільності пропозиції та коефіцієнта ймовірності. У цьому випадку як попередні коефіцієнти, так і коефіцієнти щільності пропозиції дорівнюють 1, тому R a c c e p t = R l i k e l i ч о о д.
- Намалюйте випадкове число x з рівномірного розподілу між 0 і 1. Якщо x < R a c c e p t, прийміть запропоноване значення обох параметрів; в іншому випадку відхиліть і збережіть поточне значення двох параметрів.
- Повторіть кроки 2-5 велику кількість разів.
Використовуючи дані про розмір тіла ссавців, я запустив MCMC з 10000 поколіннями, відкинувши перші 1000 як спалювання. Вибірка кожні 10 поколінь отримую оцінки параметрів $\ hat {\ sigma} _ {bayes} ^2 = 0,10$ (95% достовірний інтервал: 0,066 − 0,15) та $\ hat {\ bar {z}} (0) = 3.5$ (95% достовірний інтервал: 2,3 − 5,3; рис. 4.5).
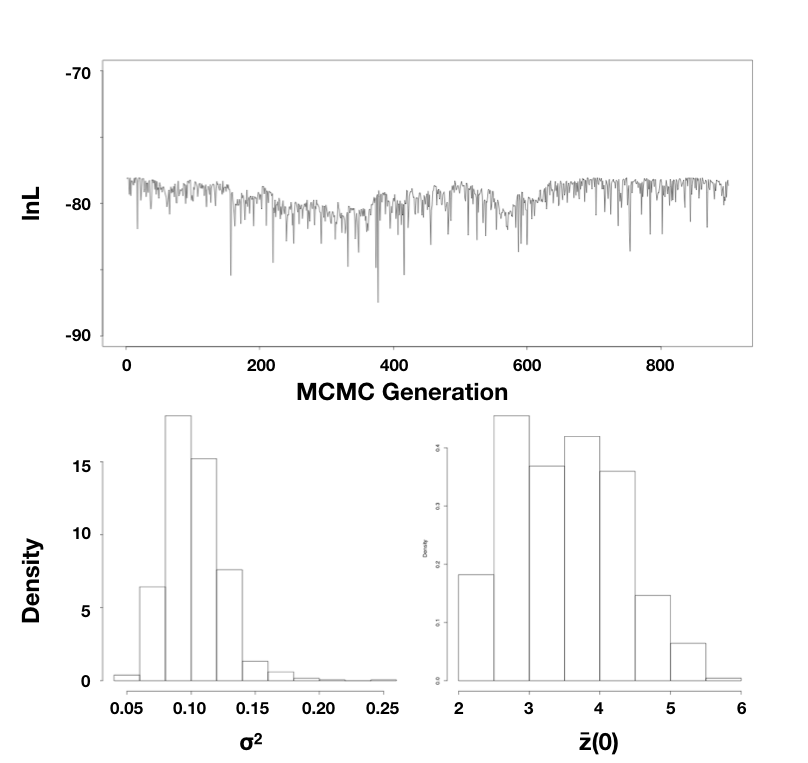
Зауважимо, що оцінки параметрів з усіх трьох підходів (REML, ML та Байєсівський) були аналогічними. Навіть довіри/достовірні інтервали трохи змінювалися, але були приблизно однакового розміру у всіх трьох випадках. Всі перераховані вище підходи математично пов'язані і повинні, в цілому, повертати аналогічні результати. Можна поставити більш високе значення на байєсівських достовірних інтервалах через довірчі інтервали від Гессіана поверхні ймовірності з двох причин: по-перше, Гессіан призводить до оцінки КІ за певних умов, які можуть бути вірними для вашого аналізу; і по-друге, байєсівські достовірні інтервали відображають загальну невизначеність краще, ніж довірчі інтервали ML (див. Розділ 2).
