3.4: Вибір в умовах невизначеності - очікувана теорія корисності

Last updated
Save as PDF

Page ID: 14062

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

У цьому розділі студент дізнається, що мета індивіда полягає в тому, щоб максимізувати очікувану корисність при прийнятті рішень в умовах невизначеності.
Ми також дізнаємося, що люди схильні до ризику, нейтральні до ризику або шукають ризик (любити).

Раніше ми бачили, що в певному світі люди люблять максимізувати корисність. У світі невизначеності здається інтуїтивним, що люди максимізують очікувану корисність. Це стосується конструкції, яка використовується для пояснення рівня задоволеності, яку людина отримує, стикаючись з невизначеним вибором. Інтуїція проста, довести її аксіоматично було дуже складним завданням. Джон фон Нейман та Оскар Моргенштерн (1944) виступали за підхід, який веде нас до формального математичного представлення максимізації очікуваної корисності.

Ми також бачили, що представлення корисної функції існує, якщо чотири припущення, розглянуті вище, тримають. Пані фон Нейман і Моргенштерн додали ще два припущення і придумали очікувану функцію корисності, яка існує, якщо ці аксіоми тримаються. У той час як дискусії про ці припущенняминазиваються припущеннями безперервності і незалежності. виходить за рамки тексту, досить сказати, що очікувана функція корисності має вигляд.

\[E(U)= \sum_{i= 1}^{n} πi Ui\]

де u - функція, яка прикріплює числа, що вимірюють рівень задоволеності u _i, пов'язаний з кожним результатом i. u називається функцією Бернуллі, а $E(U)$ це очікувана корисність функції фон Неймана - Моргенштерна.

Знову ж таки, зауважте, що очікувана функція корисності не є унікальною, але кілька функцій можуть моделювати переваги одного і того ж індивіда над заданим набором невизначених варіантів або ігор. Важливим є те , що така функція (яка відображає переваги індивіда над невизначеними іграми) існує. Очікувана теорія корисності тоді говорить, що якщо аксіоми, надані фон Нойман-Моргенштерном, задоволені, то люди поводяться так, ніби вони намагаються максимізувати очікувану корисність.

Найважливішим розумінням теорії є те, що очікуване значення результатів долара може забезпечити рейтинг варіантів, відмінних від тих, які надаються очікуваною корисністю. Тоді очікувана теорія корисності говорить, що люди повинні вибрати варіант (азартна гра або лотерея), який максимізує їх очікувану корисність, а не очікуване багатство. Те, що очікуваний рейтинг корисності відрізняється від очікуваного рейтингу багатства, найкраще пояснити на прикладі нижче.

Давайте подумаємо про людину, функція корисності якої задається$u(W)=W$ і має початкову обдарованість у розмірі 10 доларів. Ця людина стикається з наступними трьома лотереями, заснованими на киданні монети:

Таблиця 3.1 Функція корисності з початковим пожертвуванням $10
Результат (ймовірність)	Лотерея виплат 1	Виплата лотереї 2	Виплата лотереї 3
Ч (0.5)	10	20	30
Т (0,5)	−2	−5	−10
Е (Г)	4	7.5	10

Ми можемо обчислити очікуваний виграш кожної лотереї, взявши добуток ймовірності та виплати, пов'язані з кожним результатом, і підсумовуючи цей продукт за всіма результатами. Рейтинг лотерей на основі очікуваних виграшів у доларах - це лотерея 3, 2 та 1 - у такому порядку. Але давайте розглянемо рейтинг тих же лотерей цією людиною, яка ранжує їх по порядку, виходячи з очікуваної корисності.

Ми обчислюємо очікувану корисність, приймаючи добуток ймовірності та пов'язану корисність, що відповідає кожному результату для всіх лотерей. Коли виплата становить $10, остаточне багатство дорівнює початковому пожертвуванню ($10) плюс виграш = ($20). Корисність цього кінцевого багатства дається 20 = 4,472. Заповнена таблиця корисності показана нижче.

Таблиця 3.2 Рейтинг лотерей за очікуваною корисністю
Результат (ймовірність)	Утиліта Лотерея 1	Утиліта Лотерея 2	Утиліта Лотерея 3
$H(0.5)$	4.472	5.477	6.324
$T(0.5)$	2.828	2.236	0
$E(U)$=	3.650	3.856	3.162

Очікувана корисність ранжує лотереї в порядку 2—1-3. Таким чином , очікуваний принцип максимізації корисності призводить до вибору, який відрізняється від очікуваного вибору багатства.

Приклад показує, що рейтинг азартних ігор відрізняється, коли використовується теорія очікуваної корисності ($E(U)$), ніж коли застосовується$E(G)$ принцип очікуваного виграшу. Це призводить нас до розуміння того, що якщо дві лотереї забезпечують однакове$E(G)$, принцип очікуваного виграшу буде ранжувати обидві лотереї однаково, тоді як $E(U)$ теорія може призвести до унікального рейтингу двох лотерей. Що відбувається, коли$E(U)$ теорія призводить до того ж рейтингу? Теорія говорить, що людина байдужа між двома лотереями.

Типи ризиків та їх уявлення про функції корисності

Яка характеристика азартних ігор може призвести до того ж, $E(G)$ але до іншого$E(U)$? Характерним є «ризик», пов'язаний з кожною грою. На цьому етапі ми дбаємо лише про те поняття ризику, яке фіксує властиву мінливість результатів (невизначеність), пов'язану з кожною лотереєю. Тоді $E(U)$ теорія передбачає, що «ставлення» до ризику людей до кожної лотереї може призвести до різних рейтингів між лотереями. Більше того, теорія є «надійною» в тому сенсі, що вона також дозволяє ставлення до ризику варіюватися від однієї людини до іншої. Як ми зараз побачимо,$E(U)$ теорія дозволяє нам фіксувати різне ставлення людей до ризику. Технічно різниця у ставленні до ризику між окремими особами називається «неоднорідністю переваг ризику» серед економічних агентів.

З точки зору$E(U)$ теорії, ми можемо класифікувати всіх економічних агентів на одну з трьох категорій, як зазначено в «1: Природа ризику - втрати та можливості»:

Ризик несприятливий
Нейтральний ризик
Ризик шукає (або любити)

Далі ми вивчимо, як$E(U)$ фіксує ці погляди та значення кожного ставлення до ризику.

Розглянемо$E(U)$ функцію, задану\ (E (U) =\ displaystyle \ sum_ {i= 1} ^ {n} πi U (Wi)\). Нехай переваги будуть такими, що доповнення до корисності виходить з додаткового долара при нижчих рівнях багатства завжди більше, ніж додаткова корисність додаткового долара при більш високих рівнях багатства. Отже, скажімо, що коли людина має нульове багатство (немає грошей), то у людини нульова корисність. Тепер, якщо людина отримує долар, його корисність скаче до 1 util. Якщо цій людині зараз дають додатковий долар, то за припущенням монотонності (більше-краще), його корисність піде вгору. Припустимо, що вона йде до 1.414 utils так, що приріст корисності становить всього 0,414 utils, тоді як раніше це була ціла одиниця (1 util). При 2 доларах багатства, якщо індивід отримує ще один долар, то знову корисність його сімей піднімається на новий рівень, але тільки до 1.732 utils, збільшення на 0,318 одиниць (1.732 −1.414). Це збільшує корисність зі зменшенням для кожної додаткової одиниці багатства. $\PageIndex{1}$На малюнку зображений графік роботи утиліти.

Малюнок$\PageIndex{1}$: Функція корисності для особи, що не схильна до ризику

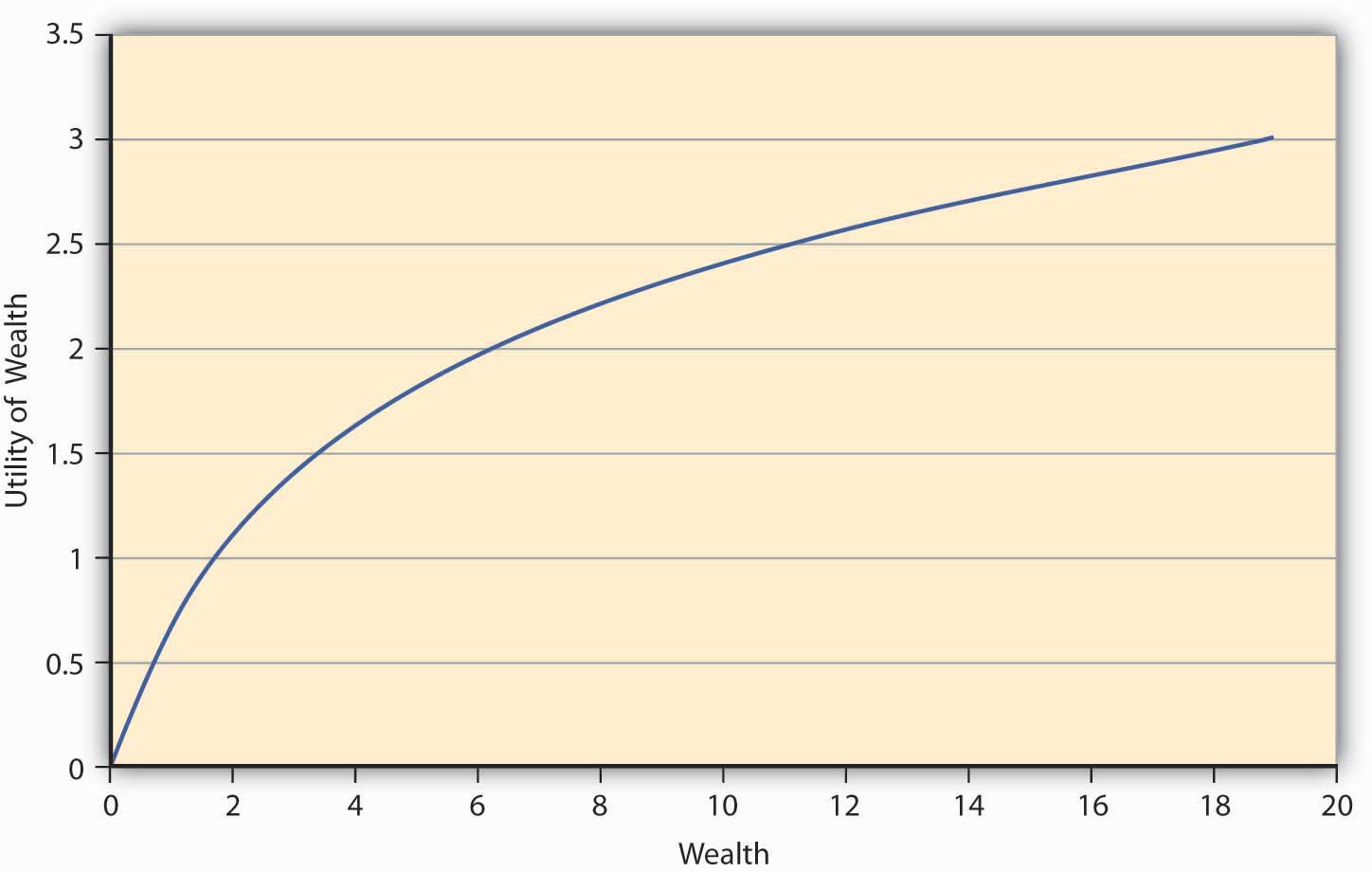
Перше, що ми помічаємо з малюнка$\PageIndex{1}$ - це його увігнутість, а це означає, що якщо намалювати хорду, що з'єднує будь-які дві точки на кривій, хорда буде лежати строго нижче кривої. Більш того, корисність завжди збільшується, хоча і зі знижуючою швидкістю. Ця особливість цієї конкретної корисної функції називається зменшенням граничної корисності. Гранична корисність при будь-якому заданому рівні багатства - це не що інше, як нахил функції корисності на цьому рівні багатства.Математично властивість, що корисність збільшується зі знижуючою швидкістю, можна записати як комбінацію обмежень на перший і другий похідні (швидкість зміни нахил) корисної функції,$u^\prime$ (W) > 0, $u^{\prime\prime}$ (W) <0. Деякі функції, що задовольняють цю властивість$u(W)= W$, є$LN(W)$,$−e −aW$. $u^\prime$(Ш) >0,$u^{\prime\prime}$ (Ш) <0,$u(W)= W$, $LN(W)$,$−e −2W$. Функціональна форма, зображена на малюнку $\PageIndex{1}$, є$LN(W)$.

Питання, яке ми задаємо собі зараз, полягає в тому, чи буде така особа, чия корисність функція має форму на малюнку$\PageIndex{1}$, готовий платити актуарно справедливу ціну (AFP), яка дорівнює очікуваним виграшам, грати в азартну гру? Нехай гра, яка пропонує йому виплати, буде запропонована йому. У грі 1, столи мають плей-офф гри по грі 1 в таблиці 3.1 на основі кидання монети. AFP за гру становить 4 долари. Припустимо, що людина на ім'я Террі несе цю вартість авансом і виграє; тоді його остаточне багатство є$$10−$4+$10= $16$ (початкове багатство мінус вартість гри, плюс виграш $10), або ж вона дорівнює\ ($10− $4− $2= $4\) (початкове багатство мінус вартість гри, мінус втрата $2) у випадку, якщо він програє. Нехай корисність функції цього індивіда буде задана W. Тоді очікувана утиліта, коли гра коштує AFP дорівнює 0.5 16 +0.5 4 =3 utils. З іншого боку, припустимо, Террі не грає в гру; його корисність залишається на рівні 10 = 3.162. Оскільки утиліта вища, коли Террі не грає в гру, ми робимо висновок, що будь-яка людина, чиї переваги зображені Фігурою,$\PageIndex{1}$ відмовиться від азартної гри, якщо її вартість дорівнює AFP. Це важливий результат для увігнутої корисної функції, як показано на малюнку$\PageIndex{1}$.

Такий людині знадобляться стимули, щоб бути готовим грати в гру. Це може відбутися як зниження ціни за гру в лотерею, або як премія, яка компенсує людині ризик. Якщо Террі вже стикається з ризиком, він заплатить суму, більшу за актуарно справедливу вартість, щоб зменшити або усунути ризик. Таким чином, це працює в обох відношеннях - споживачі вимагають премію вище AFP, щоб взяти на себе ризик. Просто так, страхові компанії стягують з фізичних осіб внески за передачу ризиків через страховки.

Індивід - назвемо його Йоганном - має переваги, які характеризуються тими, що показані на малюнку$\PageIndex{1}$ (тобто увігнутою або зменшуючою граничною функцією корисності). Йоганн - людина, що не схильна до ризику. Ми бачили, що людина, яка не схильна до ризику, відмовляється грати в актуарно чесну гру. Такі відрази від ризику також забезпечують природний стимул для Йоганна вимагати (або, еквівалентно, платити) премію за ризик вище AFP, щоб взяти на себе (або, еквівалентно, позбутися) ризику. Можливо, ви згадаєте з «1: Природа ризику - втрати та можливості», який ввів більш математичний захід до опису відрази від ризику. В експериментальному дослідженні Холт і Лорі (2002) виявляють, що більшість досліджуваних предметів зробили «безпечний вибір», тобто виявляли відраза до ризику. Оскільки реальні ситуації можуть бути більш ризикованими, ніж лабораторні установки, ми можемо сміливо припустити, що більшість людей більшу частину часу схильні до ризику. А як щодо решти населення?

Ми знаємо, що більшість з нас постійно не поводяться як люди, які не схильні до ризику. В кінці 1990-х років фондовий ринок вважався «бульбашкою», і багато людей інвестували в фондовий ринок, незважаючи на переваги, які вони виставляли до цього часу. У той час голова Ради Федеральної резервної системи Алан Грінспен ввів термін «ірраціональне багатство» у промові в Американському інституті підприємництва. Словосполучення стало регулярним способом опису відхилень людей від нормальних уподобань. Така поведінка також повторювалося на рані-середині 2000-х років з бульбашкою нерухомості. Люди без раціональних засобів купувати будинки купували їх і взяли на себе «нетрадиційні ризики», що призвело до фінансової та кредитної кризи 2008—2009 років та великих рецесій (можливо, навіть депресії), коли президент Обама вступив на посаду в січні 2009 року. Ми можемо розглядати зовнішні ринкові умови та «стадний менталітет» як значний внесок у зміну раціональних рис відрази від ризику.

Людина може піти стрибки з парашутом, дельтапланеризм, і брати участь у високому ризику прийняття поведінки. Наше питання полягає в тому, чи може очікувана теорія корисності також захопити цю поведінку? Дійсно, це може, і це підводить нас до поведінки, яка шукає ризик, та її характеристику в $E(U)$ теорії. Оскільки поведінка, яка шукає ризик, демонструє переваги , які, здається, протилежні відрази від ризику, математичне функціональне представлення може також показувати протилежну поведінку. Для людини, що любить ризик, функція корисності покаже форму, наведену на малюнку$\PageIndex{2}$. Це показує, що чим більше рівень багатства індивіда, тим вище збільшення корисності, коли людині дається додатковий долар. Ми називаємо цю особливість функції, при якій корисність завжди збільшується зі зростаючою швидкістю, збільшуючи граничну корисність. Виходить, що всі опуклі функції утиліти виглядають як Figure$\PageIndex{2}$. Крива лежить строго нижче хорди, що з'єднує будь-які дві точки на кривій. Опукла крива на малюнку$\PageIndex{1}$ має деякі приклади, які включають математичну функцію\ (u (W) = W^2\), e W. $u(W)=W^2$Е, Вт.

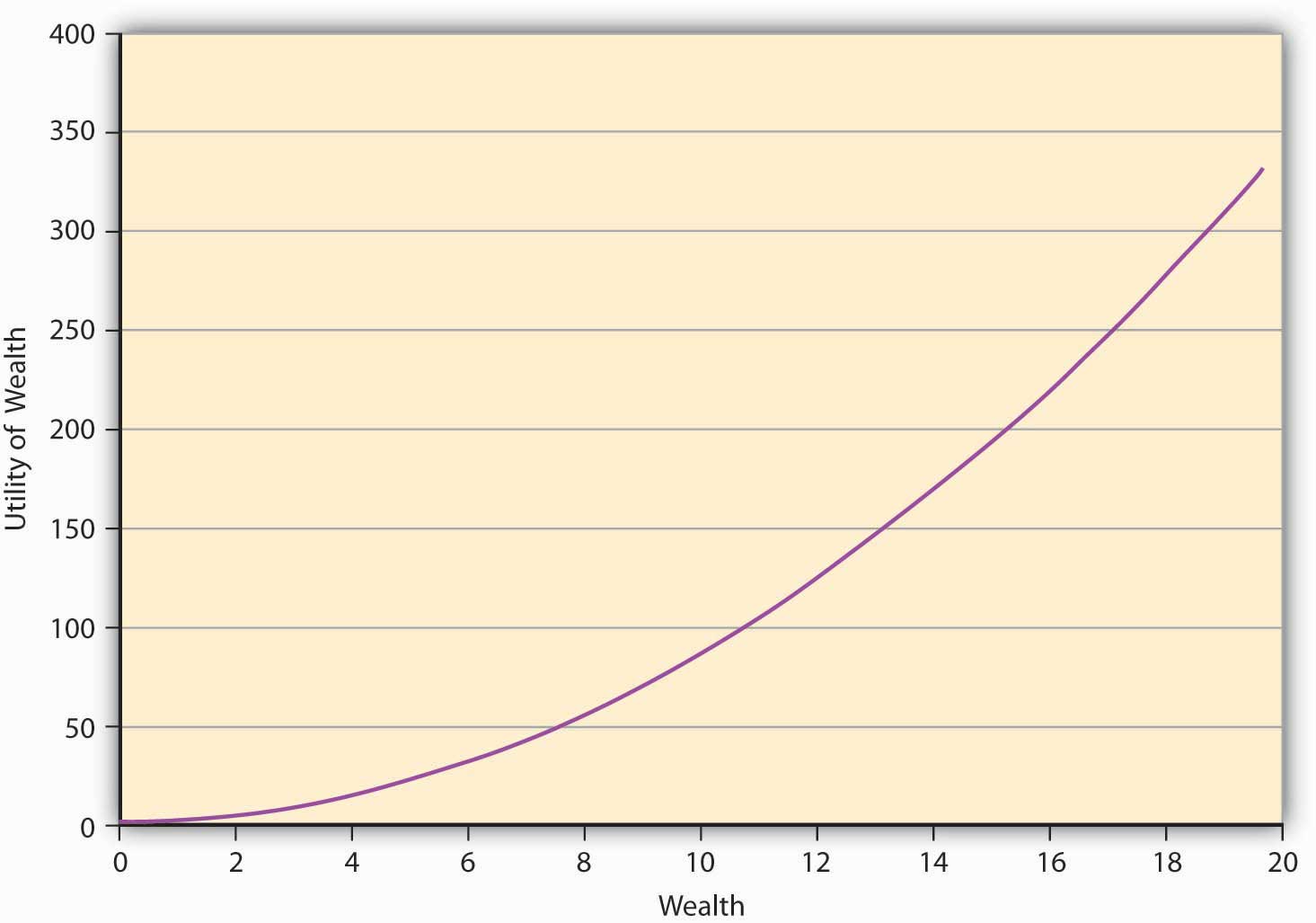
Малюнок$\PageIndex{2}$: Функція корисності для особи, яка шукає ризик

Людина, яка шукає ризик, завжди вирішить грати в азартну гру на своєму AFP. Наприклад, припустимо, що переваги індивіда віддані$u(W)= W²$. Як і раніше, фізична особа володіє 10 доларів, і повинна вирішити, чи грати в лотерею на основі кидання монети. Виплата, якщо голова повертається вгору, становить $10 і −$2, якщо це хвіст. Ми бачили раніше (в таблиці 3.1), що AFP для гри в цю лотерею становить $4.

Очікуваний розрахунок корисності виглядає наступним чином. Після перенесення вартості лотереї авансом, багатство становить 6 доларів. Якщо голови виявляються вгору, стає остаточне багатство$$16 ($6 + $10)$. Якщо хвости повертаються обличчям вгору, то остаточне багатство дорівнює $4 ($6 − $2). Очікувана корисність людей, якщо вони грають у лотерею, є\ (u (W) = 0.5 × 16 ^ 2+0.5× 4 ^ 2 = 136\) utils.

З іншого боку, якщо фізична особа на ім'я Рей вирішує не грати в лотерею, то$E(U)= 10^2=100$. Оскільки вище,$E(U)$ якщо Рей грає в лотерею на своєму AFP, він буде грати в лотерею. По суті, це розум азартних гравців. Саме тому ми бачимо так багато людей на ігрових автоматах в гральних будинках.

Контраст між вибором, зробленим особами, схильними до ризику, та особами, які шукають ризик, чітко чіткий у вищезгаданому прикладі. Математично кажучи, для людини, що не схильна до ризику, ми маємо $E(U[W])≤U[E(W)]$. Аналогічно, для людини, яка шукає ризик, ми маємо $E(U[W])≥U[E(W)]$. Цей результат називається нерівністю Йенсена. Підводячи підсумок, людина, яка шукає ризику, завжди грає в лотерею на своєму AFP, тоді як людина, яка не схильна до ризику, завжди відмовляється від неї. Їх увігнуті (рис. 3.1.1) порівняно з опуклими (рис.$\PageIndex{1}$) корисними функціями та їх наслідками лежать в основі їх прийняття рішень.

Нарешті, ми підійшли до третього типу ставлення до ризику, де людина байдужа між грою в лотерею і не грати в неї. Такого індивіда називають ризик-нейтральним. Уподобання такого індивіда можуть бути захоплені$E(U)$ теоретично лінійною функцією корисності виду$u(W)=aW$, де a - дійсне число > 0. Така людина отримує постійну граничну корисність багатства, тобто кожен додатковий долар додає таку ж корисність людині незалежно від того, наділений індивід $10 або $10,000. Функція корисності такого індивіда зображена на малюнку$\PageIndex{3}$.

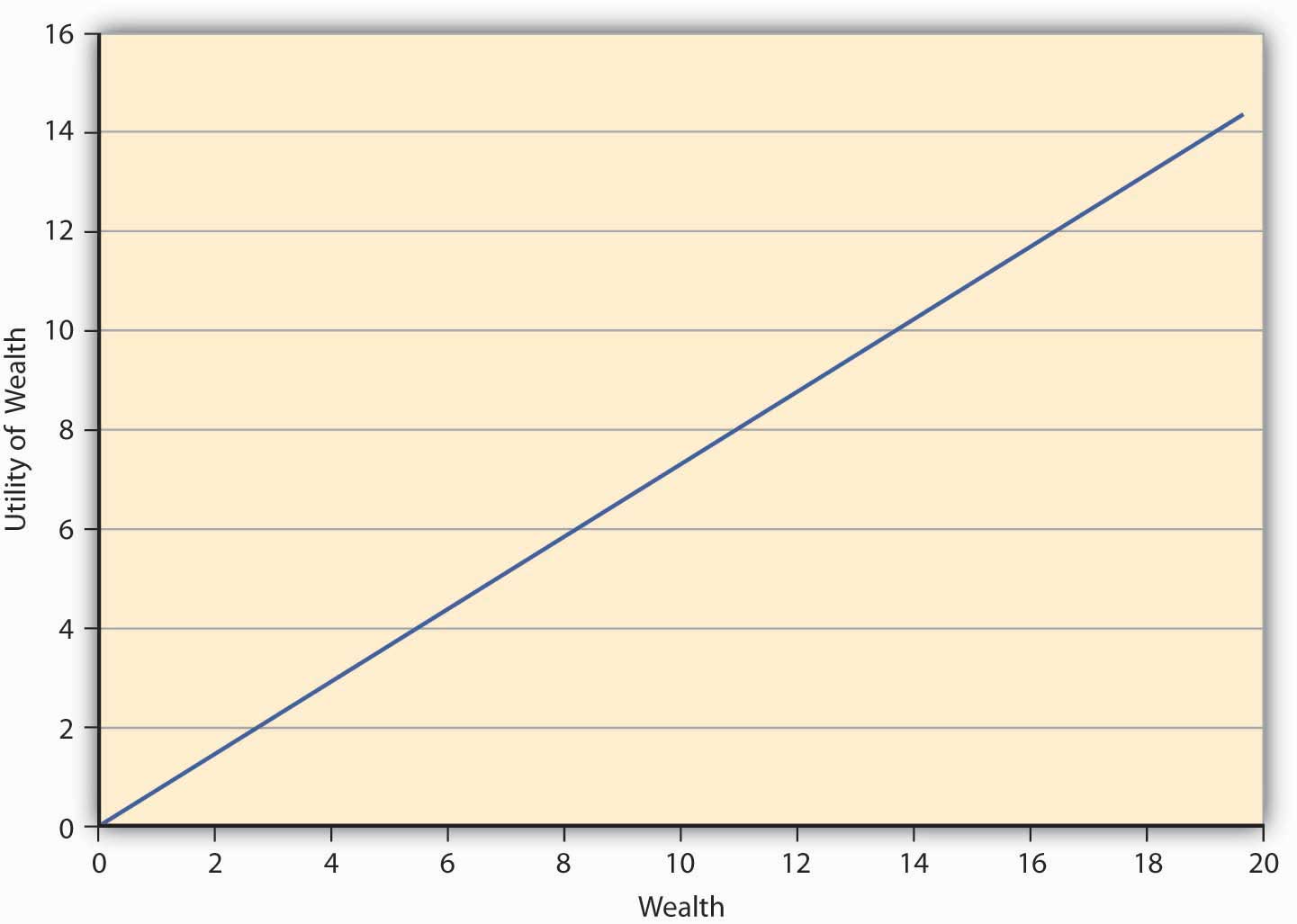Малюнок $\PageIndex{3}$: Функція корисності для особи, нейтральної від ризику

Ключові виноси

Цей розділ закладає основу для аналізу поведінки індивіда в умовах невизначеності. Студент повинен вміти описувати його як такий.
Студент повинен бути в змозі обчислити очікувані прибутки і очікувані комунальні послуги.
Нарешті, і найголовніше, увігнутість та опуклість функції корисності є ключовими для розрізнення осіб, які не схильні до ризику та шукають ризик.

Питання для обговорення

Обговоріть очікувану функцію корисності фон Нойманна-Моргенштерна та обговоріть, чим вона відрізняється від очікуваних прибутків.
Вам кажуть, що$U(W)= W^2$ це корисна функція зі зменшенням граничної корисності. Чи правильно це? Обговоріть, використовуючи визначення зменшується граничної корисності.
Фізична особа має функцію корисності, яку надає$U(W)=W$, і початкове багатство в 100 доларів. Якщо він грає в безкоштовану лотерею, в якій він може виграти або втратити 10 доларів при перевертанні монети, обчислити його очікувану корисність. Який очікуваний виграш? Чи буде така людина віднесена до категорії нейтральних ризиків?
Обговоріть три типи ризику щодо їх форм, технічної/математичної формулювання та економічної інтерпретації.

Результат (ймовірність)	Утиліта Лотерея 1	Утиліта Лотерея 2	Утиліта Лотерея 3
\(H(0.5)\)	4.472	5.477	6.324
\(T(0.5)\)	2.828	2.236	0
\(E(U)\)=	3.650	3.856	3.162