9: Збираємо все разом
- Page ID
- 29393
Дистиляція науки (суміш хімії та хімічної інженерії)
Це частина IX, Склавши все разом із десяти частин серії технічних статей про дистиляцію науки, як це зараз практикується на промисловому рівні. Див. також Частина I, Огляд вступних коментарів, обсяг серії статей та номенклатури.
Частина IX, Склавши все разом, використовує інформацію з частин III по VII, показуючи, як об'єднати їх у практичному прикладі для об'ємного поділу; і як за допомогою методів, описаних у попередніх статтях, дають відповіді, які відрізняються від ідеалів основного закону Раулта/Далтона застосування.
Дивіться попередні статті за наступними деталями:
- Частина III для критичних властивостей і ацентричного фактора, особливо табл. 3-3
- Частина IV для рекомендованого рівняння тиску пари, особливо Рівняння 4-3 та Таблиця 4-1
- Частина V для рівняння стану, особливо рівнянь 5-3 та 5-4
- Частина VI, особливо Рівняння 6-4 для парціального тиску та Рівняння 6-7 та 6-8 для коефіцієнтів нечіткості
- Частина VII для коефіцієнтів активності рідини, особливо рівняння 7-3
У цій статті розроблений практичний приклад дистиляції, показуючи взаємозв'язок Y/X з температурою для двійкової системи DCS-TCS з тиском, який тримається постійним при 11,0 атмосфер, і показує результати як графік T XY/P, а також у табличній формі. Виходячи з таких даних, конструктор ректифікаційної колони розглянув би оптимальне розташування для подачі колони, відновлення «вершин» і «днищ», підрахунку лотка і зовнішнього коефіцієнта дефлегмації (а від цього, енергії, необхідної для рекотла і конденсатора, а також гідравлічного навантаження на одиницю масового потоку сировини). Дві варіації цього прикладу відпрацьовані, показуючи застосування науки про дистиляцію: один, який використовує лише ідеальний Раулт/Далтон, і той, який використовує повний набір коефіцієнтів відходу ідеальності. Таблиця виведення і графіки нижче виконуються за допомогою MS Excel. Потім в кінці статті результати таблиці графічно продемонстровані за допомогою графіка Маккейба-Тейла, щоб відійти від лотків для відповідної швидкості дефлюксу та показати найкращий лоток подачі.
Таблиця на малюнку 9-1 створена для покриття діапазону рідкої мольної фракції ДКС від одиниці до нуля, з кроком 0,05 моль фракції, при цьому додано 0,01/0,99 моль фракції для ілюстрації асимптотичних ефектів. Для кожного ненульового рядка таблиці спочатку приймається температура, а потім парові мольні фракції, розраховані на Раулт/Далтон, з p=11,0 атмосфер; потім температуру цього рядка ітераційно регулюють до повного тиску = 11,0 атмосфер.
На графіку рисунка 9-1 наведені результати розрахунку у вигляді T XY/P, при цьому значення X DCS =1.0 представляє найбільш щільний можливий продукт «вершини» на конденсаторі ректифікаційної колони; і значення X DCS =0,0, що представляє найбільш щільний можливі «днища» продукту при колонці ребойлера, все при загальному стані дефлегмації. Для скінченного стовпця мольна частка продукту «вершини» буде обрізанням верхніх значень X DCS кривих T XY/P; а мольна частка продукту «днища» a буде обрізанням менших значень X DCS T XY /P криві. У такому випадку лоток подачі колонки буде ідентифікований як ту точку в колонці, де температура лотка ідентична температурі кипіння кормової суміші. Супровідний графік рішення показує, як виглядатимуть криві T XY/P, для такого рішення Раульт/Далтона для двійкового DCS-TCS при 11,0 атмосфер.
\( Y_{1}=(X_{1} \times VP_{1})/(X_{1} \times VP_{1} + X_{2} \times VP_{2}) \nonumber\)\( Y_{2}=(X_{2} \times VP_{2})/(X_{1} \times VP_{1} + X_{2} \times VP_{2}) \nonumber\)повторити рівняння 6-1
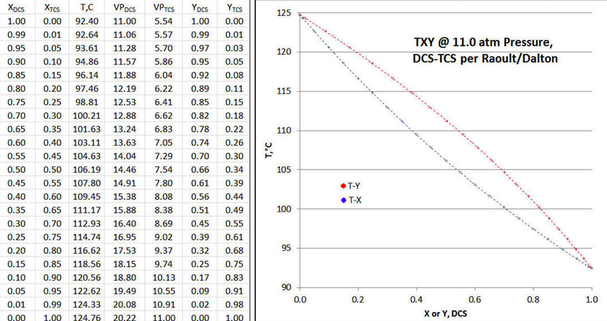
Якщо графік даних графіка рисунка 9-1 ретельно вивчений, можна побачити, що криві T- X і T- Y точно симетричні, коли «складені» вздовж лінії, що проходить від абсцис/ординатних точок (0,124,76) до (1,92,40); або «складеного» ортогонально до тієї ж лінії. Іншими словами, немає відходів від ідеальності ні в парній, ні в рідкій фазі, ні з DCS, ні TCS.
Тепер X і Y повторно обчислюються, включаючи відступи від ідеальності, як в fugacity (ø), так і коефіцієнти активності рідини (\(\gamma \nonumber\)).
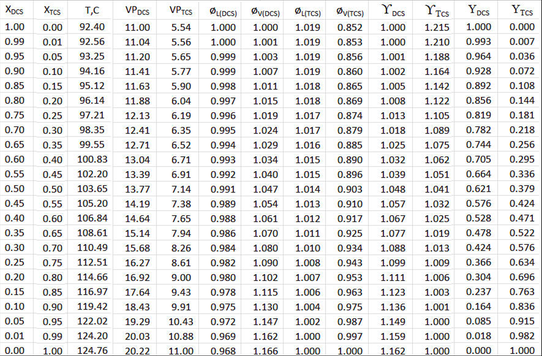
Таблиця на малюнку 9-2 аналогічним чином налаштована і розрахунки виконуються рядово для кожного значення X DCS, але коефіцієнти розпускання рідини і пари фази (ø L і ø V) і коефіцієнти активності (\(\gamma_{i} \nonumber\)) включаються в розрахунок пари моль фракції (\(\gamma_{DCS} \nonumber\)). Для кожного ряду температура повторюється до суми парціальних тисків = 11,0 атмосфер. Зауважте, що оскільки коефіцієнти активності є м'якими функціями температури, кожен рядок має свої власні константи Ван Лаара, визначені та значення\(\gamma \nonumber\) розрахованої для рідкої мольної фракції цього рядка. Таким чином, всі фактори відходу від ідеальності включені.
\[ Y_{i}= (\phi_{i}^L \times \gamma_{i} \times VP_{i} \times X_{i})/(\phi_{i}^V \times \pi) \label{9-1} \]
що є алгебраїчним перебудовою рівняння 6-4 з попередньої частини VI.
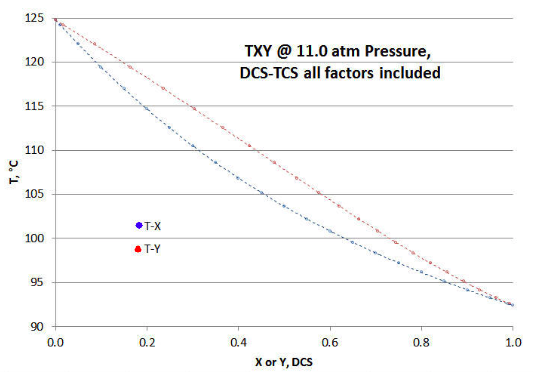
Щоб краще показати, як кілька факторів вильоту ідеальності впливають на графік T XY/P (порівняно з малюнком 9‑1 вище), побудовано таблицю на малюнку 9-2. Симетрії малюнка 9-1 Раульт/Дальтона вже немає, ні вздовж лінії «згину», що проходить від абсцис/ординатних точок (0,124,76) до (1, 92,40); або «складеної» ортогонально до тієї ж лінії. Також зверніть увагу, що криві T- X і T- Y ближче один до одного на малюнку 9‑3, на відміну від малюнка 9-1.
Для дуже простого наближення кількості лотків, для даного продукту «вершин» ректифікаційної колони, «днищ» продукту і кормової суміші мольних фракцій, а для заданої швидкості флегмації побудована ділянка Маккейба-Тіле на малюнку 9-4, щоб графічно відступити від кількості лотків вище і нижче подавального лотка. Майже для всіх промислових застосувань цей аналіз лотка за лотком проводиться за допомогою комп'ютерного моделювання, такого як ASPEN, VMG, HYSYS, ChemCAD тощо Щоб застосувати техніку до комп'ютерної моделі, користувач вкаже критичні константи (відповідно до частини III), рівняння тиску пари, яке буде використовуватися (відповідно до Частина IV), EOS, яка буде використовуватися для розрахунку коефіцієнтів нечіткості (відповідно до частини V), та модель коефіцієнта активності рідини, яка буде використовуватися (відповідно до частини VI).
Для побудови графіка Маккейба-Тіле рівновага X - Y (червоним кольором нижче) наноситься на набір осей, де X = рідка моль частка найбільш летючого компонента = X DCS; і Y = парова моль фракції найбільш летючого компонента = Y ДКС. Загальна лінія рефлюксу (чорним кольором нижче) з'єднує (X, Y) = (0,0) і (1,1); представляє максимально можливий рефлюкс. Лінії додаються (пунктирним синім кольором нижче) для подачі (X F) та продукту дистиляту (X D) та продукту днища (X B), від осі X до загальної лінії рефлюксу. Лінія подачі продовжується до кривої рівноваги, і від цього перетину проводиться лінія до кінця лінії продуктів дистиляту. Нахил цієї намальованої лінії являє собою мінімальний внутрішній флегм, необхідний для поділу (тобто з нескінченною кількістю лотків). Потім проводиться робоча лінія верхньої колони (у пурпуровому кольорі нижче), що з'єднує кінець лінії продуктів дистиляту з лінією подачі, з ухилом, дещо більшим за мінімальний нахил флегмації. У звичайній практиці нахил робочої лінії верхньої колони зазвичай приблизно в 1,3 рази перевищує мінімальний ухил, залежно від відносного значення робочої енергії проти капітальних витрат. Потім проводиться робоча лінія нижньої колонки, перетинаючи нижню лінію продукту з верхньою робочою лінією колони (і лінією подачі). Кількість теоретичних лотків (він же етапів) може бути відступений (зеленим кольором нижче) від X D до X B, і найкращий лоток визначається для подачі.
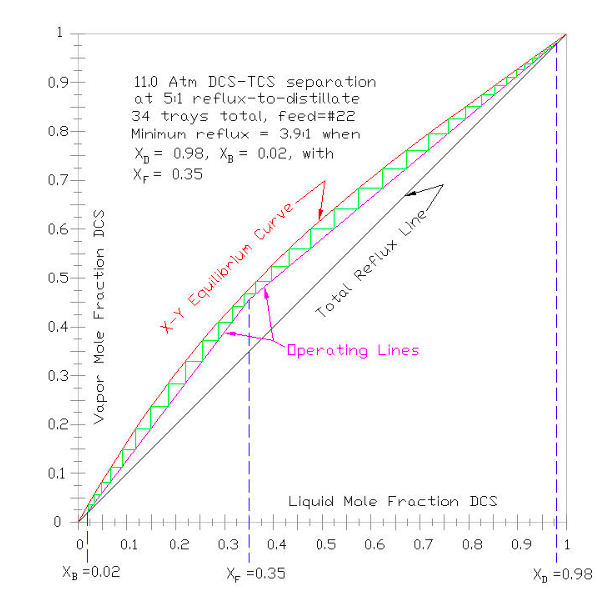
Щоб проілюструвати приклад використання ділянки Маккейба-Тіле, припустімо, що розділяється суміш - це молярна рідина 35% DCS, попередньо нагріта до температури кипіння 108,61° C (як показано на 35% малюнку 9-2). Далі припустимо, що колона «вершини» дистилятного продукту повинна бути 98% молярної ДКС, а колона «днища» продукту повинна бути 98% молярної ТКС. За текстом вище мінімальний відлив (тобто нахил лінії між X D = X DCS 0,98, X B = X DCS 0,02) визначається рівним 3. 9:1, рефлюкс-дистилят. Щоб забезпечити розумну кількість лотків, вибирається швидкість дефлегмації 5:1 (приблизно в 1,3 рази менше мінімальної), тому нахил робочої лінії верхньої колони дорівнює R/ (R+1) = 5/ (5+1) =0,8333. Відступивши від лотків, визначається, що загальна кількість необхідних теоретичних лотків становить 34, при подачі лотка на #22. Звичайний підрахунок лотка починається з конденсатора колонки = лоток #1.
Як видно, вивчаючи малюнок 9-4, оскільки швидкість рефлюксу стовпця збільшується, нахил операційної лінії верхньої колонки (пурпуровий) збільшується, і розрив відкривається між (червоною) лінією рівноваги XY та (чорною) загальною лінією рефлюксу. Так при збільшенні флегми зменшується кількість лотків, необхідних для здійснення зазначеного поділу.
У звичайному промисловому процесі всі розрахунки виконуються за допомогою комп'ютерних симуляторів, що дозволяє змінювати нахил робочої лінії; стан якості подачі (наприклад, насичена пара, насичена рідина, переохолоджена рідина тощо); зміни внутрішніх співвідношень потоку рідини/пари через фізичне властивості; теплові ефекти навколишнього середовища; ефективність лотка тощо; а також інтеграція ректифікаційної колони в решту технологічного проектування. Таким чином, метод Маккейба-Тіле просто використовується для графічного пояснення.
Однак основним розглядом конструкції ректифікаційної колони є співвідношення рівноваги XY. Якщо це значно помилково - наприклад, використання лише Raoult/Dalton - конструкція колонки буде невдалою. Враховуючи вартість систем дистиляції промислового масштабу в мільйоні доларів (десятки $ MM для більших), є всі підстави, щоб отримати співвідношення рівноваги XY правильно.
У прикладі цієї статті основна модель Раулта/Далтона призведе до того, що співвідношення рівноваги XY у наведеному вище прикладі має більшу кривизну (ніж показано на малюнку 9-4) і, отже, більш відкритий проміжок між кривою рівноваги та робочими лініями. Отриманий дефлюкс визначається буде приблизно 2/3 необхідної, а кількість необхідних лотків також становитиме близько 2/3 потреб - тому велика помилка в конструкції. З огляду на те, про що йде мова фінансово, не виникає сумніву, що використання правильної дистиляції науки того варто, навіть якщо поняття складні і розрахунки стомлюючі.
