6.5: Втома

Вступ

Поняття «втоми» виникало кілька разів у Модулі про перелом (Модуль 23), як у зростанні тріщин в літаках «Комета», що призвело до катастрофи, коли вони стали досить великими, щоб поширюватися катастрофічно, як передбачено критерієм Гріффіта. Втома, як розуміють технологи матеріалів, - це процес, при якому пошкодження накопичуються через повторюваного застосування навантажень, які можуть бути значно нижче межі текучості. Процес небезпечний тим, що одноразове застосування навантаження не призведе до жодних шкідливих наслідків, а звичайний аналіз стресу може призвести до припущення про безпеку, якої не існує.

В одному популярному поданні втоми в металах, вважається, що процес втоми починається з внутрішньої або поверхневої вади, де напруження зосереджені, і складається спочатку з зсуву потоку вздовж площин ковзання. Протягом ряду циклів це ковзання породжує вторгнення і видавлювання, які починають нагадувати тріщину. Справжня тріщина, що йде всередину від області вторгнення, може спочатку поширюватися вздовж однієї з вихідних площин ковзання, але врешті-решт повертається, щоб поширюватися поперечно до основного нормального напруження, як показано на малюнку 1.

Малюнок 1: Інтрузійно-екструзійна модель ініціювання втомної тріщини

Коли досліджується поверхня руйнування втомленого зразка, область повільного росту тріщин зазвичай проявляється у вигляді «розкладачки», концентричної навколо місця розташування початкового flf aw. (Див. Рис. 2.) Область розкладачки часто містить концентричні «пляжні знаки», при яких тріщина була заарештована протягом деякої кількості циклів, перш ніж відновити своє зростання. Зрештою, тріщина може стати достатньо великою, щоб задовольнити критерії інтенсивності енергії або напружень для швидкого поширення, слідуючи попереднім вираженням механіки руйнування. Ця кінцева фаза виробляє шорстку поверхню, характерну для швидкого руйнування. При посмертному дослідженні вийшли з ладу деталей часто можна співвіднести пляжні позначки з конкретними випадками перенапруження, а також оцінити прикладене напруження при руйнуванні від розміру тріщини безпосередньо перед швидким поширенням і в'язкістю матеріалу на руйнування.

Малюнок 2: Типові поверхні втомно-руйнування. Від Б.Чалмерс, Фізична металургія, Wiley, стор. 212, 1959.

Сучасне дослідження втоми, як правило, датується роботою О.Волера, технолога німецької залізничної системи в середині дев'ятнадцятого століття. Волер був стурбований виходом з ладу осей після різного часу експлуатації, при навантаженнях значно менше, ніж очікувалося. Вісь вагонного вагона - це, по суті, кругла балка в чотириточковому вигині, яка створює стискаюче напруження вздовж верхньої поверхні і напруження при розтягуванні уздовж дна (див. Рис. Після того, як вісь повернулася на півобороту, низ стає верхнім і навпаки, тому напруги на певній ділянці матеріалу на поверхні змінюються синусоїдально від натягу до стиснення і назад знову. Це тепер відомо як повністю зворотна втома навантаження.

Малюнок 3: Втома в вагонній осі.

S-N криві

Задовго до того, як було розроблено мікроструктурне розуміння процесів втоми, інженери розробили емпіричні засоби кількісної оцінки процесу втоми та проектування проти нього. Мабуть, найважливішою концепцією є\(S-N\) діаграма, наприклад, показана на малюнку 4 (HW Hayden, W.G. Moffatt, and J Wulff, The Structure and Properties of Materials, Vol. III, John Wiley & Sons, 1965.), в якому до зразка\(S\) застосовується постійна амплітуда циклічного напруження і визначається кількість циклів завантаження до тих пір,\(N\) поки зразок не вийде з ладу. Мільйони циклів можуть знадобитися, щоб викликати збій при нижчих рівнях навантаження, тому абсциси в зазвичай побудовані логарифмічно.

Малюнок 4:\(S - N\) криві для алюмінію і низьковуглецевої сталі.

У деяких матеріалах, зокрема чорних сплавів,\(S - N\) крива flf аттендує зрештою, так що нижче певної межі витривалості\(\sigma_e\) відмови не відбувається незалежно від того, як довго циклічні навантаження. Очевидно, що дизайнер буде розмір конструкції, щоб зберегти напруги нижче\(\sigma_e\) відповідним коефіцієнтом міцності, якщо циклічні навантаження повинні бути витримані. Для деяких інших матеріалів, таких як алюміній, обмеження витривалості не існує, і дизайнер повинен домовитися, щоб запланований термін служби конструкції був меншим, ніж точка руйнування на\(S - N\) кривій.

Статистична мінливість є клопіткою при випробуванні на втому; необхідно виміряти тривалість життя, можливо, двадцяти зразків на кожному з десяти або близько того рівнів навантаження, щоб визначити\(S - N\) криву зі статистичною впевненістю (Посібник з випробувань на втому та Статистичний аналіз даних втоми, ASTM STP-91-A, 1963 .). Як правило, неможливо цикл зразка на більш ніж приблизно 10 Гц (інерція в компонентах випробувальної машини та нагрівання зразка часто стають проблематичними при більш високих швидкостях), і на цій швидкості потрібно 11,6 днів, щоб досягти\(10^7\) циклів завантаження. Отримання повної\(S - N\) кривої, очевидно, є нудною і дорогою процедурою.

Малюнок 5: Мінливість термінів втоми та сили руйнування.

На перший погляд, розкид в виміряних життях здається величезним, особливо з огляду на лог-арифмічну шкалу абсцис. Якщо коефіцієнт мінливості при звичайному випробуванні на розтяг зазвичай становить лише кілька відсотків, чому терміни служби втоми змінюються на порядки? Потрібно пам'ятати, що при випробуванні на розтяг ми вимірюємо мінливість напруги при заданому числі циклів (один), тоді як при втомі вимірюємо мінливість в циклах при заданому напруженні. Зазначено інакше, при випробуванні на розтяг ми генеруємо вертикальні смуги розкиду, але при втомі вони горизонтальні (див. Рис. Зверніть увагу, що ми повинні очікувати більшої мінливості в тривалості життя, коли\(S - N\) крива стає f atter, так що матеріали, які менш схильні до пошкодження втоми, потребують більшої кількості зразків, щоб забезпечити заданий обмеження довіри на термін служби.

Вплив середнього навантаження

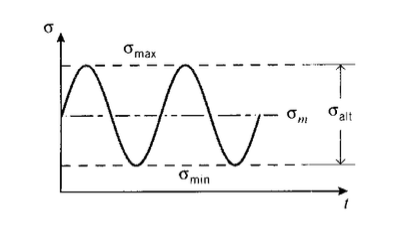
Звичайно, не всі фактичні завантаження додатків передбачають повністю зворотний цикл стресу. Більш загальний вид тестування на втому додає середнє напруження,\(\sigma_m\) на яке накладається синусоїдальний цикл, як показано на малюнку 6. Такий цикл можна сформулювати кількома способами, загальним є констатувати змінний стрес\(\sigma_{alt}\) і коефіцієнт напруги\(R = \sigma_{\min}/\sigma_{\max}\). Для повністю зворотного завантаження,\(R = -1\). Напружений цикл часто\(R = 0.1\) використовується при випробуванні компонентів літака, і відповідає циклу розтягування-натяг, в якому\(\sigma_{\min} = 0.1 \sigma_{\max}\).

Малюнок 6: Одночасне середнє і циклічне навантаження.

Для отримання\(S - N\) кривої для простого випадку повністю зворотного навантаження потрібна дуже значна кількість випробувань, і зазвичай недоцільно визначити цілі сім'ї кривих для кожної комбінації середнього та змінного напружень. Існує ряд стратегій для визначення цієї складності, однією загальною є діаграма Гудмана, показана на малюнку 7. Тут будується графік із середнім напруженням у вигляді абсциси і змінним напруженням як ординатою, а прямий «рятувальний круг» проводиться від\(\sigma_e\)\(\sigma_{alt}\) осі до граничного напруження розтягування\(\sigma_f\) на\(\sigma_m\) осі. Тоді для будь-якого заданого середнього напруги межа витривалості | значення змінного напруги, при якому перелом втоми ніколи не відбувається | можна прочитати безпосередньо як ординату рятувального кола при цьому значенні\(\sigma_m\). Крім того, якщо проектна заявка диктує задане співвідношення\(\sigma_e\) до\(\sigma_{alt}\), від початку проводиться лінія з нахилом, рівним цьому співвідношенню. Його перетин з рятувальним колом потім дає ефективну межу витривалості для цієї комбінації\(\sigma_f\) і\(\sigma_m\).

Малюнок 7: Діаграма Гудмана.

Шахтарський закон про сукупний збиток

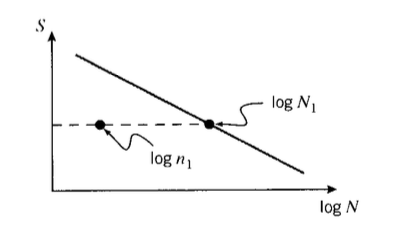
Коли рівень циклічного навантаження змінюється під час процесу втоми, часто висувається гіпотеза про кумулятивну модель пошкодження. Щоб проілюструвати, візьміть життя, щоб бути\(N_1\) циклами на рівні стресу\(\sigma_1\) і\(N_2\) в\(\sigma_2\). Якщо передбачається, що пошкодження накопичуються з постійною швидкістю під час втоми і\(n_1\) застосовується ряд циклів при напрузі\(\sigma_1\), де\(n_1 < N_1\) як показано на малюнку 8, то частка витраченого терміну служби складе\(n_1/N_1\). Щоб визначити, скільки додаткових циклів витримає екземпляр при напрузі\(\sigma_2\), буде доступна додаткова частка життя, щоб сума двох дробів дорівнювала одиниці:

\(\dfrac{n_1}{N_1} + \dfrac{n_2}{N_2} = 1\)

Зверніть увагу, що тут використовуються абсолютні цикли, а не цикли журналу. Рішення для інших циклів допустимо при\(\sigma_2\):

 

Узагальнення такого підходу називається «Закон шахтаря», і може бути написано

\[\sum \dfrac{n_j}{N_j} = 1\]

де\(n_j\) - кількість циклів, що застосовуються при навантаженні, що відповідає терміну служби\(N_j\).

Приклад\(\PageIndex{1}\)

Розглянемо гіпотетичний матеріал, в якому\(S - N\) крива лінійна від величини, рівної напрузі руйнування\(\sigma_f\) за один цикл\((\log N = 0)\), падаючи до значення\(\sigma_f/2\) at,\(\log N = 7\) як показано на малюнку 9. Таку поведінку можна описати співвідношенням

 

Матеріал піддався циклам\(n_1 = 10^5\) навантаження на рівні\(S = 0.6 \sigma_f\), і ми хочемо оцінити, скільки циклів\(n_2\) матеріал тепер може витримати, якщо ми підвищимо навантаження\(S = 0.7 \sigma_f\). З\(S - N\) відносин ми знаємо, що життя в\(S = 0.6 \sigma_f =\) постійному буде\(N_1 = 3.98 \times 10^5\) і життя в\(S = 0.7 \sigma_f =\) постійному буде\(N-2 = 1.58 \times 10^4\). Тепер застосовуючи рівняння 6.5.1:

Малюнок 9: Лінійна\(S - N\) крива.

\(\dfrac{n_1}{N_1} + \dfrac{n_2}{N_2} = \dfrac{1 \times 10^5}{3.98 \times 10^5} + \dfrac{n_2}{1.58 \times 10^4} = 1\)

\(n_2 = 1.18 \times 10^4\)

Шахтарський «закон» слід розглядати, як і багато інших матеріальних «законів», корисне наближення, досить просте в застосуванні, яке може бути досить точним для використання в дизайні. Але накопичення пошкоджень при втомі, як правило, є складною сумішшю декількох різних механізмів, і припущення про лінійне накопичення пошкоджень, властиве закону Майнера, слід розглядати скептично. Якщо частини мікроструктури матеріалу стають нездатними нести навантаження в міру прогресування втоми, напруга повинна переноситися збереженими мікроструктурними елементами. Швидкість накопичення пошкоджень в цих елементах потім збільшується, так що матеріал набагато швидше зазнає пошкоджень в останні порції свого втомного терміну служби. Якщо, з іншого боку, циклічні навантаження викликають механізми зміцнення, такі як молекулярна орієнтація або затуплення тріщин, швидкість накопичення пошкоджень може знизитися протягом деякої частини життя матеріалу. Шахтарський закон ігнорує такі ефекти, і часто не вдається вловити істотну фізику процесу втоми.

Темпи зростання тріщин

Звичайно, в літаках, але і в інших конструкціях, а також, життєво важливо, щоб інженери могли передбачити швидкість зростання тріщин під час циклічного навантаження, так що деталь, про яку йде мова, бути замінена або відремонтована до того, як тріщина досягне критичної довжини. Велика кількість експериментальних даних підтверджує думку про те, що швидкість росту тріщини може бути корельована з циклічною варіацією коефіцієнта інтенсивності напружень:

\[\dfrac{da}{dN} = A \Delta K^m\]

де\(da/dN\) швидкість росту втомних тріщин за цикл,\(\Delta K = K_{\max} - K_{\min}\) це діапазон коефіцієнта інтенсивності напружень протягом циклу\(A\) та\(m\) параметри, які залежать від матеріалу, навколишнього середовища, частоти, температури та коефіцієнта напруги. Це іноді називають «Паризьким законом», і призводить до сюжетів, подібних до того, що показано на малюнку 10.

Малюнок 10: Паризький закон про темпи зростання тріщин втоми.

Показник часто\(m\) близько 4 для металевих систем, що може бути раціоналізовано як накопичення пошкоджень пов'язане з об'ємом\(V_p\) пластичної зони: оскільки обсяг\(V_p\) зони масштабується з\(r_p^2\) і\(r_p \propto K_I^2\), то\(da/dn \propto \Delta K^4\). Деякі специфічні значення констант\(m\) і\(A\) для різних сплавів наведені в таблиці 1.

Таблиця 1: Чисельні параметри в паризькому рівнянні.

сплав	\(m\)	\(A\)
Сталь	3	\(10^{-11}\)
Алюміній	3	\(10^{-12}\)
Нікель	3.3	\(4 \times 10^{-12}\)
Титан	5	\(10^{-11}\)

Вправа\(\PageIndex{1}\)

Сталь має граничну міцність на розрив 110 kpsi і межу втомної витривалості 50 kpsi. Навантаження така, що змінна напруга дорівнює 0,4 від середнього напруження. Використовуючи метод Гудмана з коефіцієнтом запасу міцності 1,5, знайдіть величину змінного напруги, що дає безпечну експлуатацію.

Вправа\(\PageIndex{2}\)

Титановий сплав має граничну міцність на розрив 120 kpsi і межу втомної витривалості 60 kpsi. Змінне напруження становить 20 kpsi. Знайти допустиме середнє напруження, використовуючи коефіцієнт запасу міцності 2.

Вправа\(\PageIndex{3}\)

Матеріал має\(S - N\) криву, лінійну від величини, рівної напрузі руйнування\(\sigma_f\) за один цикл (\(\log N= 0\)), що падає до значення\(\sigma_f/3\) at\(\log N = 7\). Матеріал піддався циклам\(n_1 = 1000\) навантаження на рівні\(S = 0.7 \sigma_f\). Оцініть, скільки\(n_2\) циклів може витримати матеріал, якщо зараз підвищена амплітуда напруги\(S = 0.8 \sigma_f\).

Вправа\(\PageIndex{4}\)

Сталевий сплав має\(S - N\) криву, яка падає лінійно від 240 kpsi при\(10^4\) циклах до 135 kpsi при\(10^6\) циклах. Зразок завантажують при змінному напруженні 160 kpsi для\(10^5\) циклів, після чого змінне напруження підвищують до 180 kpsi. Скільки додаткових циклів при цьому більш високому стресі очікується, що зразок виживе?

Вправа\(\PageIndex{5}\)

Розглянемо тіло, досить велике, щоб вважатися нескінченним у бічному вимірі, що містить центральну наскрізну товщину тріщини спочатку довжини\(2a_0\) і піддається циклічному напруженню амплітуди\(\Delta \sigma\). Використовуючи Паризький закон (Рівняння 6.5.2), показати, що кількість циклів,\(N_f\) необхідних для зростання тріщини до довжини,\(2a_f\) задається співвідношенням

\(\ln (\dfrac{a_f}{a_0}) = A(\Delta \sigma)^2 \pi N_f\)

коли\(m = 2\), і для інших значень\(m\)

 

Вправа\(\PageIndex{6}\)

Використовуйте вираз, отриманий у Вправі,\(\PageIndex{5}\) для обчислення кількості циклів, які сталевий компонент може витримати до руйнування, де початкова довжина тріщини становить 0,1 мм, а критична половина тріщини, щоб викликати руйнування, становить 2,5 мм. Амплітуда напружень за цикл становить 950 МПа. Візьміть тріщину, щоб бути центральною тріщиною в нескінченній пластині.

Вправа\(\PageIndex{7}\)

Використовуйте вираз, розроблений у Вправи,\(PageIndex{1}\) щоб дослідити, чи краще обмежити розмір\(a_0\) початкових вад або розширити розмір\(a_f\) вади, при якому відбувається швидкий перелом. Обмеження\(a_0\) може бути зроблено за допомогою вдосконалених методів виробництва або кращих методів перевірки, а збільшення\(a_f\) може бути зроблено шляхом вибору матеріалу з більшою в'язкістю руйнування. Для «базового» випадку візьміть\(m = 3.5, a_0 = 2\ mm\),\(a_f = mm\). Обчисліть процентне збільшення,\(N_f\) дозволивши (а) початковий розмір f сировини, який потрібно зменшити до\(a_0 = 1\ mm\), і (b) збільшивши остаточний f розмір сировини до\(N_f = 10\ mm\).