6.1: Вихід і пластичний потік
- Page ID
- 30683
Вступ
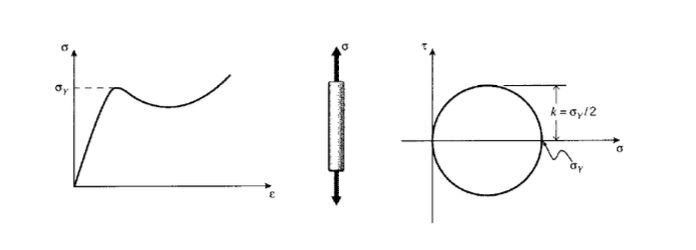
У нашому огляді кривої напруження-деформації при розтягуванні в модулі 4 ми описали вихід як постійну молекулярну перестановку, яка починається при досить високому напруженні,\(\sigma_Y\) позначеному на малюнку 1. Процес врожайності дуже залежний від матеріалу, пов'язаний безпосередньо з молекулярною рухливістю. Часто можна контролювати процес врожайності, оптимізуючи обробку матеріалів таким чином, що впливає на рухливість. Наприклад, полістирол загального призначення - це слабкий і крихкий пластик, який часто приписують надання пластмасам репутації тіньовості, яка страждає галузь роками. Це відбувається тому, що полістирол при кімнатній температурі має настільки невелику молекулярну рухливість, що він відчуває крихке руйнування при напруженнях, менших, ніж ті, які необхідні для індукування виходу з пов'язаним з ним пластичним потоком. Але коли той самий матеріал змішується з гумовими частинками відповідного розміру і складу, він стає настільки жорстким, що його використовують для ватин шоломів і надміцних дитячих іграшок. Ця магія здійснюється шляхом контролю процесу врожайності. Контроль врожайності для збалансування міцності проти ударної в'язкості є одним з найважливіших аспектів інженерії матеріалів для конструкційних застосувань, і всі інженери повинні знати про можливості.

Ще одна важлива причина для розуміння врожайності більш прозаїчна: якщо матеріалу не дають поступитися, він навряд чи вийде з ладу. Це не стосується крихких матеріалів, таких як кераміка, які руйнуються перед тим, як вони дають, але в більшості більш жорстких конструкційних матеріалів ніяких пошкоджень не відбувається до виходу. Загальноприйнятою практикою проектування є розмір конструкції таким чином, щоб зберегти напруження в пружному діапазоні, не допускати виходу відповідним коефіцієнтом міцності. Тому ми повинні бути в змозі передбачити, коли врожайність буде відбуватися в загальних багатовимірних напружених станах, враховуючи експериментальне значення\(\sigma_Y\).
Руйнування рухається нормальними напруженнями, що діють на відокремлення однієї атомної площини від іншої. Вихід, навпаки, приводиться в рух напругами зсуву, ковзаючи одну площину уздовж іншої. Ці два різних механізми проілюстровані на малюнку 2. Звичайно, облігації повинні бути розірвані під час ковзання, пов'язаного з прибутковістю, але на відміну від перелому дозволено реформуватися на нових позиціях. Цей процес може призвести до суттєвих змін у матеріалі, навіть призводячи в кінцевому підсумку до руйнування (як при згинанні металевого стрижня назад і вперед багаторазово, щоб зламати його). «Пластична» деформація, яка лежить в основі врожайності, є, по суті, в'язким процесом потоку і слідує кінетичним законам, досить схожим на рідини. Як і потік в рідинях, пластичний потік зазвичай відбувається без зміни обсягу, що відповідає співвідношенню Пуассона\(ν = 1/2\).

Багатовісні напружні стани
Межа плинності зазвичай\(\sigma_Y\) визначається при випробуванні на розтяг, де діє одне одновісне напруження. Однак інженер повинен вміти прогнозувати, коли вихід відбудеться в більш складних реальних ситуаціях, пов'язаних з багатовісними напруженнями. Це робиться за допомогою критерію врожайності, спостереження, отриманого з експериментальних доказів щодо того, що йдеться про стресовий стан, який викликає врожайність. Один з найпростіших з цих критеріїв, відомий як максимальне напруження зсуву або критерій Треска, стверджує, що вихід виникає, коли максимальне напруження зсуву досягає критичного значення\(\tau_{\max} = k\). Чисельне значення\(k\) для даного матеріалу може бути визначено безпосередньо в чистому випробуванні на зсув, наприклад, крутіння кругового вала, але його також можна знайти опосередковано від випробування на розтяг. Як показано на малюнку 3, коло Мора показує, що максимальне напруження зсуву діє на площину,\(45^{\circ}\) віддалену від осі розтягування, і становить половину напруги розтягування за величиною; тоді\(k = \sigma_Y/2\).
У випадках плоского напруження коло Мора дає максимальне напруження зсуву в цій площині як половину різниці головних напружень:
\[\tau_{\max} = \dfrac{\sigma_{p1} - \sigma_{p2}}{2}\]
Приклад\(\PageIndex{1}\)
Використовуючи\(\sigma_{p1} = \sigma_{\theta} = pr/b\) і\(\sigma_{p2} = \sigma_{z} = pr/2b\) в 6.1.1, напруга зсуву в циліндричному посудині під тиском із закритими кінцями становить (див. Модуль 6)
де\(\theta_z\) індекс вказує на напругу зсуву в площині, дотичній до стінки судини. Виходячи з цього, ми можемо очікувати, що посудина під тиском вийде, коли
\(\tau_{\max , \theta_z} = k = \dfrac{sigma_Y}{2}\)
які виникли б при тиску
\(p_Y = \dfrac{4b\tau{\max , \theta_z}}{r} \overset{?}{=} \dfrac{2b\sigma_Y}{r}\)
Однак цей аналіз помилковий, як видно, малюючи кола Мора не тільки для площини\(\theta_z\), але\(\theta_r\) і\(rz\) площин, як показано на малюнку 4.

Напруження зсуву в\(\theta_r\) площині видно вдвічі більше, ніж у\(\theta_z\) площині, оскільки в\(\theta_r\) площині друге основне напруження дорівнює нулю:
Таким чином, вихід буде відбуватися в\(\theta_r\) площині при тиску\(b\sigma_Y/r\), половина значення, необхідного для отримання врожайності в\(\theta_z\) площині. Неврахування напружень зсуву, що діють у цьому третьому напрямку, призведе до серйозно недопродуманого судна.
Ситуації, подібні до цього прикладу, трапляються в плоских напруженнях, коли основні напруги в\(xy\) площині мають один і той же знак (як розтягування, так і обидві стискаючі). Максимальне напруження зсуву, яке контролює вихід, становить половину різниці між основними напруженнями; якщо вони обидва мають однаковий знак, ще більша напруга зсуву виникне на перпендикулярній площині, що містить більшу з головних напружень у площині xy.
Ця концепція може бути використана для малювання «локусу врожайності», як показано на малюнку 5, конверт у\(\sigma_1 - \sigma_2\) координатах, поза яким прогнозується вихід. Цей локус, очевидно, перетинає осі координат при значеннях, відповідних напрузі текучості при розтягуванні\(\sigma_Y\). У I і III квадрантах основні напруги мають один і той же знак, тому відповідно до максимального критерію напруги зсуву вихід визначається різницею між більшим головним напруженням і нулем. У II і IV квадрантах локус задається\(\tau_{\max} = |\sigma_1 - \sigma_2|/2 = \sigma_Y /2\), так що\(\sigma_1 - \sigma_2\) = const; це дає прямі діагональні лінії, що йдуть\(\sigma_Y\) від однієї осі до\(\sigma_Y\) іншої.
Малюнок 5. Локус виходу для критерію максимального напруження зсуву.
Приклад\(\PageIndex{2}\)
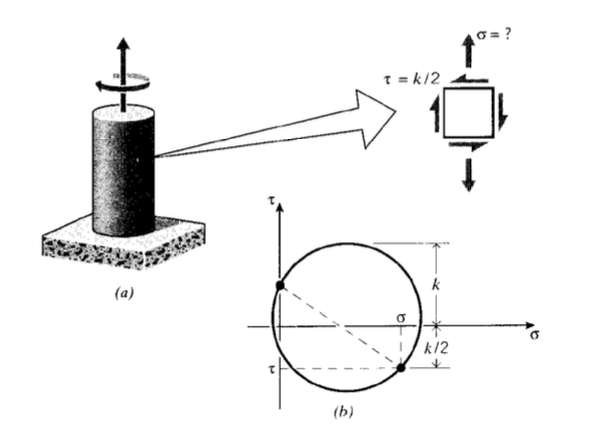
Круглий вал піддається крутному моменту в половину, який необхідний для спричинення врожайності, як показано на малюнку 6; тепер ми запитуємо, яке напруження при розтягуванні може бути застосовано одночасно, не викликаючи виходу.
Коло Мора малюється з напруженням зсуву\(\tau = k/2\) та невідомим напруженням розтягування\(\sigma\). Використовуючи критерій граничного зсуву Tresca, вихід буде відбуватися, коли\(\sigma\) такий, що
\(\tau_{\max} = k = \sqrt{(\dfrac{\sigma}{2})^2 + (\dfrac{k}{2})^2}\)
\(\sigma = \sqrt{3} k\)
Критерій Треска зручно використовувати на практиці, але дещо краще підходить до експериментальних даних часто можна отримати за критерієм «фон Мізеса», при якому рушійною силою виходу є енергія деформації, пов'язана з девіаторичними компонентами стресу. Напруга фон Мізеса (також називається еквівалентним або ефективним напруженням) визначається як
З точки зору основних напружень це
де відмінності напружень в дужках пропорційні максимальним напруженням зсуву на трьох головних площинях (Деякі автори використовують коефіцієнт, відмінний від 1/2 в межах радикала. Це несуттєво, так як буде поглинатися при розрахунку критичного значення\(\sigma_M\)) (Так як величини зведені в квадрат, порядок напружень всередині дужок неважливий.) Напруга Мізеса також може бути записана в компактній формі з точки зору другого інваріанту тензора девіаторного напруження\(\Sigma_{ij}\):
\[\sigma_M = \sqrt{3\Sigma_{ij} \Sigma_{ij}/2}\]
Можна показати, що це пропорційно повній енергії деформації спотворення в матеріалі, а також напруженню зсуву αoct на «октаедричній» площині, орієнтованої однаково на 1-2-3 осі. Напруга фон Мізеса є рушійною силою пошкодження багатьох пластичних інженерних матеріалів, і зазвичай обчислюється більшістю комерційних кодів аналізу напружень кінцевих елементів.
Значення напруги фон Мізеса,\(\sigma_{M,Y}\) необхідне для спричинення текучості, може бути визначено з межі текучості при розтягуванні\(\sigma_Y\), оскільки в напрузі на межі текучості у нас є\(\sigma_1 = \sigma_Y\),\(\sigma_2 = \sigma_3 = 0\). Тоді
Отже, значення напруги фон Мізеса, необхідного для спричинення врожайності, таке ж, як і простий напруга текучості при розтягуванні.
Напруга плинності зсуву аналогічно\(k\) можна знайти, вставивши основні напруги, що відповідають стану чистого зсуву, у рівняння Мізеса. Використовуючи\(k = \sigma_1 = -\sigma_3\) і\(\sigma_2 = 0\), ми маємо
\(k = \dfrac{\sigma_Y}{\sqrt{3}}\)
Зверніть увагу, що цей результат відрізняється від випадку Tresca, в якому ми мали\(k = \sigma_Y/2\).
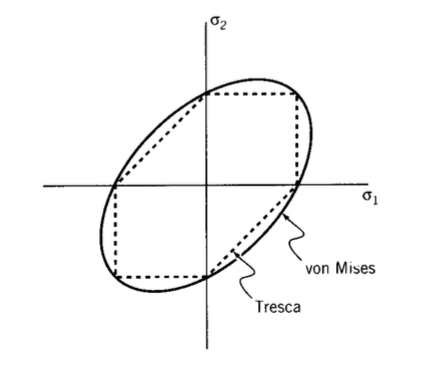
Критерій фон Мізеса також може бути побудований як локус врожайності. Так само, як критерій Tresca, він повинен проходити\(\sigma_Y\) по кожній осі. Однак він відображає як еліпс, а не призматичну форму критерію Трески (див. Рис. 7).
Вплив гідростатичного тиску
Оскільки в обговоренні дотепер вихід регулювався лише напругою зсуву, не має значення, чи є одновісне напруження стискаючим або розтягуючим; вихід відбувається, коли\(\sigma = \pm \sigma_Y\). Це відповідає гідростатичній складовій напруги\(-p = (\sigma_x + \sigma_y + \sigma_z)/3\), яка не впливає на плинність, яка експериментально вважається справедливою для ковзання в металевих системах. Полімери, однак, набагато більш стійкі до поступливості в стискаючих напружених станах, ніж при розтягуванні. Атомістичні рухи, що лежать в основі ковзання в полімерах, можна розглядати як вимагають «вільного об'єму», коли молекулярні сегменти рухаються, і цей вільний об'єм зменшується напруженнями стиснення. Таким чином, важко сформувати тверді полімери шляхом деформаційної обробки, такої як штампування та кування так само, як сталь може бути сформована; це одна з причин, чому переважна більшість автомобільних панелей кузова продовжують виготовлятися зі сталі, а не з пластику.

Ця залежність від гідростатичного напруження може бути змодельована шляхом модифікації критерію плинності, щоб заявити, що вихід відбувається, коли
\[\tau_{\max} \text{ or } \sigma_M \ge r_0 + A_p\]
де\(\tau_0\) і\(A\) є константами. Зі\(p\) збільшенням (гідростатична складова напруги стає більш позитивною) напруга зсуву, необхідна для виходу, також стає більшою, оскільки є менший вільний об'єм і більше перешкод для молекулярного руху. Ефект цієї модифікації полягає в тому, щоб ковзати еліпс фон Мізеса, щоб поширитися менше в I квадрант і більше в III квадрант, як показано на малюнку 8. Це показує графічно, що для плинності при стисненні потрібні більші напруги, а менші напруги в розтягуванні.

Кілька аморфних склоподібних полімерів - зокрема полістиролу, поліметилметакрилату та полікарбонату - піддаються механізму виходу під назвою «crazing», в якому довгі подовжені порожнечі створюються всередині матеріалу за допомогою процесу кавітації на розтяг. На малюнку 9 показано захоплення полістиролом, вирощеним у пластифікуючої рідини поблизу\(T_g\). Порожнечі, або божевілля, мають товщину приблизно 1000А і мікрони або більше в довжину, і візуально виглядають так само, як звичайні
тріщини. Вони відрізняються від тріщин, однак, тим, що широкі грані поразки охоплюються великою кількістю витягнутих фібрил, які були витягнуті з полімеру, коли захоплення відкривається. Формування фібрили вимагає зсувного потоку, але процес також дуже залежить від вільного об'єму. Запропоновано успішний багатовісний критерій напружень для розчеплення, який включає обидві ці особливості (С.Штернштейн та Л.Онгчін, Полімерні препринти, 10, 1117, 1969.) форми
Ліва сторона цього співвідношення пропорційна напрузі зсуву, а знаменник у другому члені з правого боку пов'язаний з гідростатичною складовою напруги. Зі збільшенням гідростатичного натягу зменшується зсув, необхідний для спричинення розтріскування. Параметри\(A\) і\(B\) регулюються, і обидва залежать від температури. Це співвідношення виглядає як batwing на діаграмі локусу врожайності, як показано на малюнку 10, наближаючись до\(45^{\circ}\) діагоналі, проведеної через II та IV квадранти. Crazing відбувається праворуч від кривої; зверніть увагу, що crazing ніколи не відбувається в стискаючих полах напружень.
Малюнок 10: Конверти Штернштейна для стискання та пригнічення тиску зсуву.
Crazing - це механізм врожайності, але він також осаджує крихкий перелом, оскільки висота захоплення збільшується, а фібрили доводяться до розриву. Точка, де локус захоплення перетинає локус, що поступається зсуву, є типом механічно індукованого пластично-крихкого переходу, оскільки режим відмови переходить від зсуву, що поступається, до захоплення крихкості. Екологічні агенти, такі як ацетон, що розширюють вільний об'єм в цих полімерах, значно посилюють тенденцію до захоплення крихкістю. І навпаки, такі модифікації, як включення гумових частинок, які стабілізують захоплення і не дають їм стати справжніми тріщинами, можуть забезпечити чудову в'язкість. Частинки гуми не тільки стабілізують захоплення, вони також спричиняють значне збільшення кількості захоплень, тому поглинання енергії утворення захоплення може також додати в'язкості. Це основа «ударостійкого полістиролу», або HIPS, згаданого на початку цієї глави.
Вплив швидкості і температури
Процес врожайності можна розглядати як конкуруючий з руйнуванням, і залежно від того, який процес має найнижчі вимоги до напруги, буде домінувати. Оскільки матеріал стає все менш мобільним, наприклад, за рахунок зниження температури або збільшення кількості та герметичності хімічних зв'язків, врожайність стає все складнішою. Процес перелому зазвичай набагато менше залежить від рухливості. Як плинність, так і напруження руйнування зазвичай збільшуються зі зниженням температури, але вихід більш залежний від температури (див. Рис. Це означає, що нижче критичної температури (званої пластично-крихкою температурою переходу TDB) матеріал руйнується, перш ніж він дасть. Кілька помітних збоїв у судах та трубопроводах сталися під час зимових температур, коли сталі, що використовуються при їх виробництві, були підкреслені нижче їх TDB і, таким чином, не змогли протистояти катастрофічному зростанню тріщин. У полімерах температура пластично-крихкого переходу часто збігається з температурою скляного переходу. Зрозуміло, що нам потрібна інженерна модель, здатна показати, як врожайність залежить від температури, і один популярний підхід викладено нижче.
Процеси виходу термічно активуються, рухаються напругою, подібно до потоку в'язких рідин. Навіть не вдаючись у багато подробиць щодо специфіки рухів, можна записати досить ефективні вирази для залежності цих рухів від швидкості деформації і температури. З точки зору Айрінга термічно активованих процесів, енергетичний бар'єр\(E_Y^*\) повинен бути подоланий, щоб рух продовжувався. (Ми будемо використовувати зірочку верхній індекс, щоб вказати активацію

параметри, а\(Y\) індекс тут вказує на процес дохідності.) Напруга діє на зниження бар'єру, коли він діє у напрямку потоку, і піднімає його, коли він протистоїть потоку.
Розглянемо тепер тест на постійну швидкість деформації (\(\dot{\epsilon}\)= const), в якому напруга підвищується, поки не відбудеться вихід при\(\sigma = \sigma_Y\). На межі текучості ми маємо\(d\sigma/d\epsilon = 0\), тому досягається рідинноподібний стан, при якому може відбуватися приріст деформації без відповідного поступового збільшення напруги. Аналогічно з теоріями швидкості для в'язкого потоку рівняння швидкості Ейрінга може бути записано для процесу отримання як
\[\dot{\epsilon} = \dot{\epsilon_0} \exp \dfrac{-(E_Y^* - \sigma_Y V^*)}{kT}\]
\(k\)Ось константа Больцмана і\(V^*\) є фактором, що регулює ефективність стресу в зниженні бар'єру активації. Він повинен мати одиниці об'єму,\(\sigma_Y V^*\) щоб продукт мав одиниці енергії, і називається «об'ємом активації» процесу. Взявши колоди і переставляючи,
\(\dfrac{\sigma_Y}{T} = \dfrac{E_Y^*}{V*T} + \dfrac{k}{V^*} \ln \left(\dfrac{\dot{\epsilon}}{\dot{\epsilon_0}}\right)\)
Отже, ділянки\(\sigma_Y/T\) проти\(\ln \dot{\epsilon}\) повинні бути лінійними з нахилом,\(k/V^*\) як показано на малюнку 12, з якого можна обчислити обсяг активації. Горизонтальний інтервал між двома лініями при різних температурах\(T_1\) і\(T_2\) дає енергію активації:
Видимі обсяги активації в полімерах знаходяться близько 5000\(\dot{A}\), набагато більше, ніж у одиниці повторення. Це прийнято для вказівки на те, що вихід полімерів передбачає кооперативний рух декількох сотень повторних одиниць.
Приклад\(\PageIndex{3}\)
Межа плинності для полікарбонату повідомляється на рівні 60 МПа при кімнатній температурі (\(23^{\circ}C\)=\(296^{\circ}K\)), і ми хочемо знати його значення на рівні\(0^{\circ}C\) (273\(^{\circ}K\)), зберігаючи швидкість деформації однаковою.
Це може бути досягнуто шляхом написання Equation 4 з двічі, один раз для кожної температури, а потім розділивши один на інший. Параметри\(\dot{\epsilon}\) і\(\dot{\epsilon_0}\) скасування, залишаючи
З даних на малюнку 12 параметри активації прибутковості становлять\(E_Y^* = 309\ kJ/mol\),\(V^* = 3.9 \times 10^{-3}\ m^3/mol\). Використовуючи їх разом з\(R = 8.314\ J/mol\) і\(\sigma_Y^{296} = 60 \times 10^6\ N/m^2\), ми маємо
Малюнок 12: Графік Айрінга, що показує залежність межі плинності від температури та швидкості деформації в полікарбонаті (від Н.Г. Маккрама, C.P. Buckley та C.B. Bucknall, Принципи полімерної інженерії, Oxford University Press, 1988).
\(\sigma_Y^{273} = 61.5\ MPa\)
Континуальна пластичність
Теорія пластичності, яка спрямована на визначення напружень і переміщень в структурах, всі або частина яких були напружені за межі текучості, є важливим аспектом механіки твердого тіла. Ситуація як матеріально, так і геометрично нелінійна, тому це не банальна затія. Однак у таких областях, як обробка металів, теорія пластичності надала цінне розуміння. Ми окреслимо лише кілька аспектів цієї галузі в наступних параграфах, щоб представити деякі основні поняття, які читач може розширити в майбутньому дослідженні.
пластична деформація
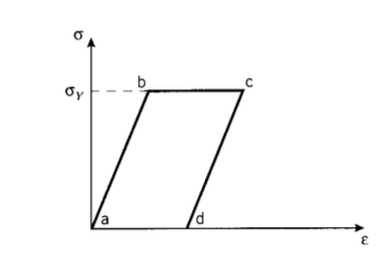
Корисна ідеалізація при моделюванні пластичної поведінки змушує матеріал бути лінійно еластичним до межі текучості, як показано на малюнку 13, а потім «ідеально пластичним» при деформаціях, що виходять за межі виходу. Штами до виходу (лінія між точками\(a\) і\(b\)) відновлюються, і матеріал розвантажується по тій же еластичній лінії, за якою він слідував під час навантаження; це звичайна пружна реакція. Але якщо матеріал напружений за межі текучості (точки\(b\)), то «пластичне» напруження за межі b відбувається при постійному напруженні і є невідновним. Якщо матеріал напружений до точки,\(c\) а потім розвантажується, він йде по шляху cd (лінія, паралельна вихідній пружній лінії\(ab\)), а не повертається вздовж\(cba\). Коли напруга була доведена до нуля (точка\(d\)), пластична деформація і залишається залишковою деформацією.
Пластична деформація може генерувати «залишкові» напруги в конструкціях, внутрішні напруги, які залишаються навіть після зняття зовнішніх навантажень. Щоб проілюструвати це, розглянемо два стрижні, що мають різні криві напруження-деформації, з'єднані паралельно (тому їх деформації завжди рівні), як показано на малюнку 14. Коли стрижні напружені до межі текучості стрижня B (точка а на осі деформації), стрижень\(A\) зазнає величини постійної пластичної деформації\(\epsilon^p\). Коли прикладене навантаження знімається, стрижень\(B\) розвантажується по своїй початковій кривій напруження-деформації, але стрижень\(A\) слідує шляхом, паралельним його вихідній пружній лінії. Коли стрижень\(A\) досягне нульового напруги (точки\(b\)), стрижень все одно\(B\) буде в напрузі (точка\(c\)). Для того щоб навантаження, що передається стрижнями разом, прийшла до нуля, стрижень\(B\) буде тягнути стрижень\(A\) в стиснення до тих\(-\sigma_B = -\sigma_A\) пір, поки не вказано точками\(d\) і\(e\). Залишкові напруги залишають в стрижнях, а вузол в цілому залишають з залишковим розтягуванням.

Залишкове напруження при стисненні може бути цінним, якщо конструкція повинна нести розтягуючі навантаження. Подібно до того, як швидке гартування може бути використано для виготовлення захисного скла шляхом стиснення поверхонь, пластична деформація може бути використана для створення сприятливих напружень на стиск. Одна відома така техніка називається «автофретаж»; це метод, який використовується для зміцнення гарматних стволів проти розриву шляхом тиску на них зсередини, щоб привести внутрішню частину стовбура в пластиковий діапазон. Коли тиск знімається, внутрішні частини залишаються зі стискаючим залишковим напруженням так само, як і з баром\(A\) у наведеному вище прикладі.
волочіння дроту
Щоб кількісно оцінити процес пластичного потоку більш детально, розглянемо далі «креслення» дроту (GW Rowe, Елементи теорії металообробки, Edward Arnold, Лондон, 1979.), при якому дріт протягується через редукційну матрицю так, щоб зменшити його площу поперечного перерізу від\(A_0\) до,\(A\) як показано на малюнку 15. Оскільки обсяг зберігається під час пластичної деформації, це відповідає осьовому подовженню\(L/L_0 = A_0/A\). Враховуючи напружений стан простим одновісним натягом, ми маємо

\(\sigma_1 = \sigma_Y, \sigma_2 = \sigma_3 = 0\)
де 1 позначає напрямок по проводу і 2 і 3 - поперечні. Робота, виконана при розтягуванні дроту з кроком довжини dL, на одиницю об'єму матеріалу, становить
\(dU = \dfrac{dW}{AL} = \dfrac{\sigma_Y A dL}{AL}\)
Інтегруючи це від\(L_0\)\(L\) до отримання загальної роботи:
\(U = \int_{L_0}^{L} dU = \dfrac{FdL}{AL} = \sigma_Y \ln \dfrac{L}{L_0}\)
Величина\(ln(L/L_0)\) - логарифмічна деформація,\(\epsilon_T\) введена в Модулі 4 (криві напруження-деформації).
Приклад\(\PageIndex{1}\)
Логарифмічна деформація може бути записана як збільшенням довжини, так і зменшенням площі, через сталість обсягу при пластичній деформації:\(\epsilon_T = \ln (L/L_0) = \ln (A_0/A)\). З точки зору зменшення діаметра відношення\(A = \pi d^2/4\) призводить до
\(e_T = \ln (\dfrac{\pi d_0^2/4}{\pi d^2/4}) = 2\ln (\dfrac{d_0}{d})\)
Беручи розмір клітини перліту, щоб зменшити пропорційно діаметру, ми очікуємо, що міцність\(\sigma_f\) дроту буде змінюватися відповідно до співвідношення Холл-Петча с\(1/\sqrt{d}\). Тоді співвідношення між міцністю дроту та логарифмічною деформацією креслення
\(\sigma_f \propto \dfrac{\exp (\epsilon_T/4)}{\sqrt{d_0}}\)
Робота, виконана постійною силою тяги\(F\) при витягуванні\(L_0\) початкової довжини дроту до нової довжини\(L\), є\(W = FL\). Це повинно дорівнювати роботі на одиницю обсягу, виконаної в матриці, помноженої на загальний обсяг дроту:
\(FL = (AL) \sigma_Y \ln \dfrac{L}{L_0}\)
Написано з точки зору зменшення площі, це
\(F = A \sigma_Y \ln \dfrac{A_0}{A}\)
Цей простий результат корисний при оцінці вимог волочіння дроту, хоча він нехтує фактичним складним полем потоку всередині матриці та впливом тертя на стінки матриці. І тертя на поверхні, і обмеження для протікання всередині поля підвищують силу, необхідну для малювання, але даний аналіз служить для встановлення нижньої межі наближення. Це часто пишуть з точки зору напруги креслення\(\sigma_1 = F/A\) та коефіцієнта зменшення площі\(r = (A_0 - A)/A_0 = 1 - (A/A_0)\):
Зверніть увагу, що напруга малювання для зменшення невеликої площі менше, ніж межа текучості при розтягуванні. Насправді максимальне зменшення площі, яке може бути досягнуто за один прохід, можна оцінити, вирішуючи значення,\(r\) яке доводить напругу витягування до значення межі текучості, яке воно, очевидно, не може перевищувати. Цей розрахунок дає
Отже, максимальне зменшення площі становить приблизно 63%, припускаючи ідеальне змащення на матриці. Це лікування нижніх обмежень дає оптимістичний результат, але не далеко від приблизно 50% зменшення, яке часто використовується як практична межа. Якщо матеріал твердне при витягуванні, максимальне зменшення може бути трохи більше.
Поля ковзання
У випадках плоского деформації існує графічна техніка, яка називається теорією лінії ковзання (W. Johnson and P.B. Mellor, Plasticity for Mechanical Engineers, Van Nostrand Co., New York, 1962.), яка дозволяє більш детально вивчити поля пластичного потоку та навантаження, необхідні для їх створення. Можуть бути включені обмеження тертя та внутрішнього потоку, тому отримані верхні межі наближення, які забезпечують більш консервативні оцінки сил, необхідних при деформації. Значний досвід необхідний, щоб освоїти цей метод, але далі будуть викладені деякі основні ідеї.
Розглянемо площину деформації в площині 1-3, без деформації в напрямку 2. Існує напруга Пуассона в напрямку 2, заданий
Так як\(v = 1/2\) в пластичному потоці,
\(\sigma_2 = \dfrac{1}{2} (\sigma_1 + \sigma_3)\)
Гідростатична складова напруги тоді
\(p = \dfrac{1}{3} (\sigma_1 + \sigma_2 + \sigma_3) = \dfrac{1}{2} (\sigma_1 + \sigma_3) = \sigma_2\)
Звідси напруга Пуассона\(\sigma_2\) в напрямку нульової деформації є середнім показником двох інших напружень\(\sigma_1\) і\(\sigma_2\), а також дорівнює гідростатичної складової напруги. Напружений стан можна задати з точки зору максимального напруження зсуву, яке є якраз\(k\) під час пластичного потоку, і накладеного гідростатичного тиску\(p\):
\(\sigma_1 = -p + k\),\(\sigma_2 = -p\),\(\sigma_3 = -p -k\)
Так як напруга зсуву дорівнює\(k\) всюди, то задача полягає в тому, щоб визначити напрямки\(k\) (напрямок максимального зсуву, по якому відбувається ковзання), і величини\(p\).
Графічна техніка передбачає замальовування ліній, які лежать уздовж напрямків\(k\). Оскільки максимальні напруги зсуву діють на дві ортогональні площини, буде два набори цих ліній, завжди перпендикулярних один одному і називаються\(\alpha\) -lines і\(\beta\) -lines. Напрямок цих ліній задається кутом нахилу\(\phi\). Будь-який зручний нахил може бути використаний для\(\phi = 0\) бази, а ідентифікація\(\alpha\) - проти\(\beta\) -ліній така, щоб зробити напруження зсуву позитивним відповідно до звичайної конвенції. Оскільки тиск\(p\) змінюється від точки до точки, існує відповідна варіація кута\(\phi\), задана рівняннями Хенкі як
\(p + 2k\phi = C_1 =\)постійна, вздовж\(\alpha\) -лінії
\ (\ бета\) -лінія</p lt-анг-44550">
Отже, тиск можна визначити за кривизною ліній ковзання, як тільки константа відома.
Поле лінії ковзання повинно підкорятися певним обмеженням на межах:
1. Вільні поверхні: Оскільки не може бути напруги, нормального до вільної поверхні, ми можемо покласти\(\sigma_3 = 0\) туди, а потім
\(p = k, \sigma_1 = -p -k = -2k\)
Отже, тиск, як відомо, є лише силою текучості зсуву на вільній поверхні. Далі- більше, так як напрямки нормальний і тангенціальний до поверхні є основними напрямками, напрямки максимального зсуву повинні бути нахилені по відношенню\(45^{\circ}\) до поверхні.
2. Поверхня без тертя: Напруга зсуву повинна бути нульовою дотичною до поверхні без тертя, що знову ж таки означає, що тангенціальний та нормальний напрямки повинні бути основними напрямками. Отже, лінії ковзання повинні відповідати поверхні в\(45^{\circ}\). Однак взагалі буде напруга, що діє нормально на поверхню, тому\(\sigma_3 \ne 0\) і при цьому не\(p\) буде дорівнює\(k\).
3. Ідеально шорстка поверхня: Якщо тертя настільки високе, щоб запобігти будь-якому тангенціальному руху на поверхні, зсув повинен бути максимальним у напрямку, який також є дотичним до поверхні. Один набір ліній ковзання потім повинен бути тангенціальним до поверхні, а інший встановити нормаль до неї.
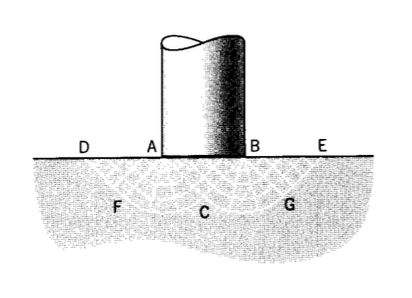
Розглянемо плоский відступ шириною b, що вдавлюється в напівнескінченний блок, з незначним тертям (див. Рис. 16). Оскільки лінії ковзання повинні відповідати поверхні індентора на\(45^{\circ}\), ми можемо намалювати трикутне поле потоку\(ABC\). Оскільки всі лінії в цій області прямі, коливань тиску бути не може\(p\), а поле є одним з «постійних станів». Це не може бути повною мірою поля, однак, оскільки воно буде обмежено як вертикально, так і збоку жорстким металом. Поле повинно поширюватися на вільні поверхні, прилеглі до пуансона, щоб рух вниз під пуансоном можна було компенсувати прилеглим до нього висхідним потоком. Ще дві трикутні області\(ADF\) і\(BEG\) додаються, які задовольняють граничним умовам на вільних поверхнях, і вони з'єднані з центральними трикутними областями «вентиляторами»\(AFC\) і\(BCG\). Вентилятори дуже корисні в конструкціях ковзання; вони, як правило, зосереджені на особливостях, таких як точки\(A\) і\(B\) де немає визначеної норми до поверхні.
Тиск на перфоратор, необхідний для встановлення цього поля, може бути визначено за лініями ковзання, і це одне з основних їх застосувань. Так як ВЕ є вільною поверхнею,\(\sigma_3 = 0\) там і\(p = k\). Тиск залишається постійним вздовж лінії,\(EG\)\(\phi\) оскільки не змінюється, але у міру\(\phi\) зменшення вздовж кривої\(GC\) (криві лінії за годинниковою стрілкою) тиск повинен збільшуватися відповідно до рівняння Хенкі. У точці\(C\) він обертався,\(-\pi/2\) так що тиск є
\(p_C + 2k\phi = p_C + 2k (-\dfrac{\pi}{2}) =\)постійна =\(p_G = k\)
\(p_C = k(1 +\pi)\)
Тиск залишається незмінним по лініях\(CA\) і\(CB\), тому тиск вздовж поверхні перфоратора також є\(k(1 + \pi)\). Таким чином, загальне напруження, що діє вгору на грані удару, є
\(\sigma_1 = p +k =2k(1 + \dfrac{\pi}{2})\)
Ставлення тиску пуансона до межі текучості при розтягуванні\(2k\) становить
\(\dfrac{\sigma_1}{2k} = 1 + \dfrac{\pi}{2} = 2.571\)
Коефіцієнт 2.571 являє собою збільшення межі текучості на розрив, спричинене геометричними обмеженнями на поле потоку під пуансоном.
Випробування на твердість по Брінеллю схожий на сценарій удару, що поступається вище, але використовує тверду сталеву сферу замість плоского індентора. Твердість по Брінеллю\(H\) розраховується як навантаження, прикладене до пуансона, розділене на проектовану площу відступу. Аналіз тесту Брінелля дещо відрізняється геометрією, але дає результат не сильно відрізняється, ніж у плоского пуансона:
Це співвідношення є дуже корисним при оцінці межі текучості металів за допомогою простих неруйнівних випробувань твердості на вдавлювання.
Вправа\(\PageIndex{1}\)
Відкрита посудина під тиском виготовлена з алюмінію, діаметром 0,3 м і товщиною стінки 3 мм. (Відкритий в цьому контексті означає, що обидва кінці посудини з'єднані з іншими конструктивними частинами, здатними витримувати тиск, як у шлангу, з'єднаному між двома резервуарами.) Визначте внутрішній тиск, при якому посудина буде поступати відповідно до критеріїв (а) Треска і (б) фон Мізеса.

Вправа\(\PageIndex{2}\)
Повторіть попередню проблему, але з посудиною під тиском зараз закритий.

Вправа\(\PageIndex{3}\)
Сталева пластина покрита тонким шаром алюмінію з обох сторін при кімнатній температурі, а потім температура підвищується. При якому підвищенні температури\(\Delta T\) вийде алюміній?

Вправа\(\PageIndex{4}\)
Якщо температура в попередній проблемі піднімається\(40\{circ} C\) понад значення, при якому відбувається врожайність, і після цього знижується назад до кімнатної температури, яке залишкове напруження залишається в алюмінії?
Вправа\(\PageIndex{5}\)
Мідний сплав піддається напруженому стану\(\sigma_x = 100\),\(\sigma_y = -200\),\(\tau_{xy} = 100\) (все в МПа). Визначте, чи відбуватиметься врожайність відповідно до (a) Tresca та (b) критерієм фон Мізеса.
Вправа\(\PageIndex{6}\)
Повторіть попередню проблему, але з напруженим станом\(\sigma_x = 190\),\(\sigma_y = 90\),\(\tau_{xy} = 120\) (все в МПа).
Вправа\(\PageIndex{7}\)
Тонкостінна трубка поміщається в одночасному натягу і крученні, викликаючи напружений стан, як показано тут. Побудувати графік\(\tau /\sigma_Y\) vs.,\(\sigma /\sigma_Y\) при якому врожайність буде відбуватися за критерієм (a) Tresca та (b) фон Мізеса. (\(\sigma\)це межа текучості при розтягуванні.)

Вправа\(\PageIndex{8}\)
Твердий круглий сталевий вал завантажується ремінними шківами на обох кінцях, як показано на малюнку. Визначте діаметр вала, необхідний для уникнення виходу за критерієм фон Мізеса, з коефіцієнтом запасу міцності 2.

Вправа\(\PageIndex{9}\)
Для полікарбонату кінетичні параметри в 6.1.4 знайдені є\(\dot{\epsilon_0} = 448 s^{-1}\)\(E_Y^* = 309\ kJ/mol\), і\(V* = 3.9 \times 10^{-3}\ m^3/mol\). Знайти межу плинності\(\sigma_Y\) при швидкості деформації\(\dot{\epsilon} = 10^2 s^{-1}\) і температурі\(40^{\circ}C\).
Вправа\(\PageIndex{10}\)
Межі плинності (в МПа) вимірювали при різних швидкостях деформації та температурах наступним чином:
| \(\dot{epsilon} = 10^{-3} s^{-1}\) | \(\dot{epsilon} = 10^{-1} s^{-1}\) | |
| \(T = 0^{\circ} C\) | 54.1 | 62.7 |
| \(T = 40^{\circ} C\) | 42.3 | 52.1 |
Визначте обсяг активації для процесу прибутковості. Яке фізичне значення може мати цей параметр?
Вправа\(\PageIndex{11}\)
Межа плинності полімеру вимірюється рівним 20 МПа при температурі 300К і швидкості деформації\(10^{-3}s^{-1}\). Коли швидкість деформації подвоюється від цього значення, межа плинності спостерігається збільшення на 10%. Який видимий обсяг активації прибутковості в даному випадку?
Вправа\(\PageIndex{12}\)
Показати напругу фон Мізеса можна записати в індексні позначення як\(\sigma_M = \sqrt{3 \Sigma_{ij} \Sigma_{ij}/2}\)
Вправа\(\PageIndex{13}\)
Зразок лінійного поліетилену випробовували при одноосному навантаженні при\(T = 23^{\circ} C\) і\(\dot{\epsilon} = 10^{-3}s^{-1}\). \(\sigma_Y\)Встановлено, що напруга плинності становить 30,0 МПа при розтягуванні та 31,5 МПа при стисненні. Визначте постійну залежності тиску\(A\) в рівнянні 3.
Вправа\(\PageIndex{14}\)
Круговий вал радіусом R піддається крутному моменту\(T\).
(а) Яке значення\(T\) буде достатньо великим, щоб викликати врожайність на зовнішній поверхні?
(b) Оскільки значення\(T\) збільшується за межі рівня, знайденого в (а), визначте радіус re, в межах якого матеріал все ще знаходиться в еластичному діапазоні.
(c) Яке значення\(T\) зробить вал повністю пластичним; тобто\(r_e = 0\)?
Вправа\(\PageIndex{15}\)
Двоелементний кроквяний каркас споруджується зі сталі з показаною геометрією. Яке навантаження\(P\) може підтримувати каркас, не поступаючись ні в одному елементі?

Вправа\(\PageIndex{16}\)
Триелементний кроквяний каркас споруджується зі сталі з показаною геометрією. Яке навантаження\(P\) може підтримувати каркас до того, як всі три елементи дадуть?
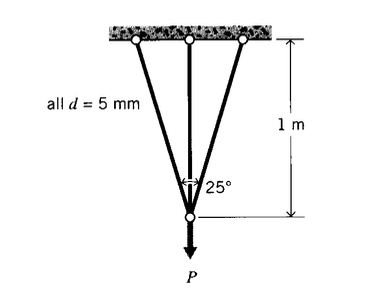
Вправа\(\PageIndex{17}\)
Якщо каркас попередньої задачі завантажується до тих пір, поки всі три елементи не дадуть, а навантаження потім зменшиться до нуля, знайдіть залишкове напруження в центральному елементі.
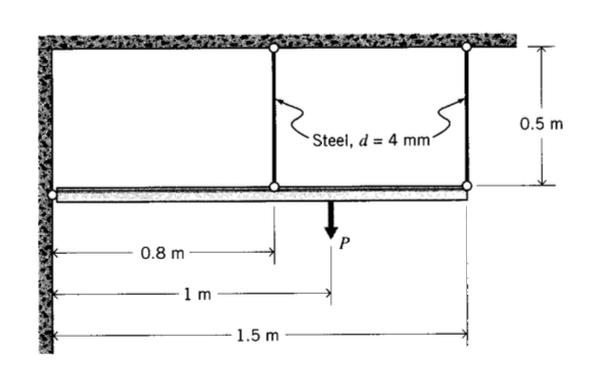
Вправа\(\PageIndex{18}\)
Жорстка балка шарнірна на одному кінці, як показано, і підтримується двома вертикальними стрижнями, як показано на малюнку.
(а) Яке навантаження\(P\) може підтримувати конструкцію до того, як обидва вертикальні стрижні дадуть?
(b) Яке залишкове напруження у вертикальних стрижнях після зниження навантаження до нуля?
Вправа\(\PageIndex{19}\)
Оцініть силу витягування, необхідну для зменшення діаметра\(0.125''\) алюмінієвого стрижня на 50% в операції волочіння дроту.
