6.4: Вступ до механіки руйнувань
- Page ID
- 30680
Вступ
У 1983 році Національне бюро стандартів (нині Національний інститут науки і техніки) та Меморіальний інститут Баттеля (R.P. Reed et al., NBS Special Publication 647-1, Вашингтон, 1983.) оцінили витрати на відмова через перелом в $119 млрд на рік в доларах 1982 року. Долари важливі, але вартість багатьох невдач у житті людини і травм нескінченно більше.
Збої сталися з багатьох причин, включаючи невизначеність у навантаженні або навколишньому середовищі, дефекти матеріалів, недоліки в проектуванні та недоліки в будівництві або технічному обслуговуванні. Конструкція проти руйнування має свою технологію, і це дуже активна область сучасних досліджень. Цей модуль надасть вступ до важливого аспекту цієї галузі, оскільки без розуміння руйнування методи аналізу напружень, розглянуті раніше, були б малокорисними. Ми зупинимося на переломах через просте перенапруження при розтягуванні, але дизайнер знову попереджається про необхідність враховувати абсолютно якомога більше факторів, які можуть призвести до відмови, особливо коли життя знаходиться під загрозою.
Модуль на основі дислокації виходу (Модуль 21) показує, як міцність конструкційних металів - особливо сталі - може бути збільшена до дуже високих рівнів шляхом маніпулювання мікроструктурою, щоб гальмувати рух дислокації. На жаль, це робить матеріал в- складчасто-крихким, так що тріщини можуть утворюватися і поширюватися катастрофічно з дуже невеликим попередженням. На жаль, кількість інженерних катастроф пов'язана безпосередньо з цим явищем, і інженери, які беруть участь у проектуванні конструкцій, повинні знати про процедури, доступні в даний час для захисту від крихкого руйнування.
Центральна складність проектування проти руйнування в високоміцних матеріалах полягає в тому, що наявність тріщин може змінити локальні напруги до такої міри, що аналіз пружних напружень, проведений настільки ретельно дизайнерами, недостатній. Коли тріщина досягає певної критичної довжини, вона може катастрофічно поширюватися через структуру, навіть якщо велике напруження набагато менше, ніж зазвичай спричиняє вихід або збій у зразку на розтяг. Термін «механіка руйнування» відноситься до життєво важливої спеціалізації в механіці твердого тіла, в якій передбачається наявність тріщини, і ми хочемо знайти кількісні співвідношення між довжиною тріщини, властивою матеріалу стійкістю до росту тріщин, і напругою, при якій тріщина поширюється з високою швидкістю до викликати структурний збій.
Підхід до енергетичного балансу
Коли А.А. Гріффіт (1893—1963) розпочав свої новаторські дослідження руйнування скла в роках безпосередньо до 1920 року, він знав про роботу Інгліса з розрахунку концентрації напружень навколо еліптичних отворів, і, природно, розглядав, як це може бути використано при розробці фундаментального підходу до прогнозування перелому сильні сторони. Однак рішення Інгліса представляє математичну складність: в межі ідеально гострої тріщини напруги наближаються до нескінченності на кінчику тріщини. Це, очевидно, нефізично (насправді матеріал, як правило, зазнає деякої локальної врожайності, щоб затупити кінчик тріщини), і використання такого результату передбачало б, що матеріали матимуть майже нульову міцність: навіть при дуже малих прикладених навантаженнях напруги біля кінчиків тріщин стануть нескінченними, і зв'язки там будуть розрив. Замість того, щоб зосереджуватися на напруженнях тріщин безпосередньо, Гріффіт застосував підхід енергетичного балансу, який став одним з найвідоміших розробок у матеріалознавстві (А.А. Гріффіт, Філософські транзакції, Серія А, Том 221, стор. 163—198, 1920. Важливість роботи Гріффіта в переломі була значною мірою невизнана до 1950-х років. див J.E. Гордон, Наука структур і матеріалів, Наукова американська бібліотека, 1988, для особистого розповіді про історію Гріффіта.).
Енергія деформації на одиницю об'єму напруженого матеріалу становить
\(U^* = \dfrac{1}{V} \int f\ dx = \int \dfrac{f}{A} \dfrac{dx}{L} =\int \sigma d\epsilon\)
Якщо матеріал лінійний (\(\sigma = E_{\epsilon}\)), то енергія деформації на одиницю об'єму дорівнює
\(U^* = \dfrac{E_{\epsilon}^2}{2} = \dfrac{\sigma^2}{2E}\)
Коли тріщина переросла в тверде тіло на глибину, область матеріалу\(a\), що прилягає до вільних поверхонь, розвантажується, і виділяється його енергія деформації. Використовуючи рішення Inglis, Гріффіт зміг обчислити, скільки енергії це.

Простий спосіб візуалізації цього викиду енергії, проілюстрований на малюнку 1, полягає в тому, щоб розглядати дві трикутні області біля боків тріщин шириною\(a\) та висотою\(\beta_a\), як повністю розвантажені, тоді як решта матеріалу продовжує відчувати повний стрес\(\sigma\). Параметр\(\beta\) можна вибрати так, щоб погодитися з рішенням Інгліса, і виходить, що для плоского напруженого навантаження\(\beta = \pi\). Загальна енергія деформації, що\(U\) виділяється, тоді енергія деформації на одиницю об'єму разів перевищує об'єм в обох трикутних областях:
\(U = -\dfrac{\sigma^2}{2E} \cdot \pi a^2\)
Тут розмір, нормальний до\(x-y\) площини, приймається як одиниця, так\(U\) і енергія деформації, що виділяється на одиницю товщини зразка. Ця енергія деформації звільняється зростанням тріщин. Але при утворенні тріщини зв'язки повинні бути розірвані, і необхідна енергія зв'язку фактично поглинається матеріалом. Поверхнева енергія,\(S\) пов'язана з тріщиною довжини\(a\) (і одиничною глибиною), становить:
\(S = 2 \gamma a\)
де\(\gamma\) - поверхнева енергія (наприклад, Джоуль/метр\(^2\)) і коефіцієнт 2 необхідний, оскільки утворилися дві вільні поверхні. Як показано на малюнку 2, загальна енергія, пов'язана з тріщиною, тоді є сумою (позитивної) енергії, поглиненої для створення нових поверхонь, плюс (негативна) енергія деформації, звільнена, дозволяючи областям поблизу флангів тріщини розвантажуватися.

Оскільки тріщина зростає довше (\(a\)збільшується), квадратична залежність енергії деформації від а врешті-решт домінує над поверхневою енергією, і за межами критичної довжини тріщини ac система може знизити свою енергію, дозволяючи тріщині рости ще довше. Аж до того моменту\(a = a_c\), коли, тріщина буде рости тільки в тому випадку, якщо напруга в підвищена. Поза цією точкою зростання тріщин є спонтанним і катастрофічним.
Значення критичної довжини тріщини можна знайти, встановивши похідну загальної енергії\(S+U\) в нуль:
Оскільки швидкий перелом неминучий, коли ця умова виконується, ми пишемо наголос як\(\sigma_f\). Рішення,
\(\sigma_f = \sqrt{\dfrac{2E_{\gamma}}{\pi a}}\)
Оригінальна робота Гріффіта стосувалася дуже крихких матеріалів, зокрема скляних стрижнів. Коли матеріал проявляє більшу пластичність, лише врахування поверхневої енергії не дозволяє забезпечити точну модель руйнування. Пізніше цей дефіцит був усунений, принаймні частково, незалежно Ірвіном (G.R. Irwin, «Динаміка руйнування», «Розрив металів», Американське товариство металів, Клівленд, 1948.) та Оруван (E. Orowan, «Розлом і міцність твердих тіл», Звіт про прогрес у фізиці, Том 12, 1949.). Вони припустили, що в пластичному матеріалі велика частина - насправді переважна більшість - виділеної енергії деформації поглиналася не шляхом створення нових поверхонь, а шляхом розсіювання енергії через пластичний потік у матеріалі біля кінчика тріщини. Вони припустили, що катастрофічний руйнування відбувається, коли енергія деформації виділяється зі швидкістю, достатньою для задоволення потреб всіх цих енергій «потоків», і позначають цю критичну швидкість викиду енергії деформації параметром\(\mathcal{G}_c\); рівняння Гріффіта потім можна переписати у вигляді:
\[\sigma_f = \sqrt{\dfrac{E\mathcal{G}_c}{\pi a}}\]
Цей вираз дуже стисло описує взаємозв'язок між трьома важливими аспектами процесу руйнування: матеріалом, про що свідчить швидкість\(\mathcal{G}_c\) вивільнення енергії критичної деформації\(\sigma_f\); рівень напруги; і розмір вади.\(a\) У ситуації проектування можна вибрати значення a на основі найменшої тріщини, яка може бути легко виявлена. Тоді для даного матеріалу з пов'язаним з ним\(\mathcal{G}_c\) значенням можна\(\sigma_f\) було б визначити безпечний рівень напруги. Потім структура буде розміщена таким чином, щоб робоче напруження було зручно нижче цього критичного значення.
Приклад\(\PageIndex{1}\)
Історія літака Dehavilland Comet початку 1950-х років, в якому принаймні два літаки розпалися в польоті, забезпечує трагічне, але захоплююче розуміння важливості теорії зламів. Це моторошна історія, а також, будучи все, але передбачено в романі 1948 року Невіл Шут під назвою No Highway. Пізніше книга стала фільмом, в якому знявся Джеймс Стюарт як наполегливий металург, переконаний, що новий літак його компанії («Північний олень») смертельно схильний до втоми металу. Коли всього через кілька років Комета була визначена мати майже саме цю проблему, і книга, і фільм стали досить відомими в матеріалознавчому співтоваристві.
Посмертне дослідження проблем комети було одним з наймасштабніших в інженерній історії (T. Bishop, Metal Progress, Vol. 67, pp. 79—85, травень 1955 р.). Це вимагало порятунку майже всього літака від розкиданих уламків на дні океану, а також передбачало повномасштабну герметизацію літака в гігантському резервуарі для води. Незважаючи на те, що були засвоєні цінні уроки, важко переоцінити шкоду, нанесену компанії Dehavilland та британській авіаційній промисловості загалом. Іноді стверджують, що тривале переважання США в комерційних літаках обумовлено хоча б частково бідою Комети.
Літак Comet мав фюзеляж з плакованого алюмінію, з\(\mathcal{G}_c \approx 300\) in-psi. Напруга обруча внаслідок відносного тиску в салоні становила 20 000 фунтів на квадратний дюйм, і при цьому напрузі довжина тріщини, яка буде поширюватися катастрофічно, становить
\[a = \dfrac{\mathcal{G}_c E}{\pi \sigma^2} = \dfrac{(300)(11 \times 10^6)}{\pi (20 \times 10^3)^2} = 2.62'' \nonumber\]
Тріщина, імовірно, буде виявлена при звичайному огляді задовго до того, як вона може вирости до такої довжини. Але у випадку з Кометою тріщини поширювалися від отворів для заклепок біля вікон кабіни. Коли тріщина дійшла до вікна, розмір віконного отвору був ефективно доданий до довжини тріщини, що призвело до катастрофи.
Сучасні літаки побудовані з урахуванням цього режиму відмови, і мають «розривні смуги», які нібито здатні зупинити будь-яку швидко зростаючу тріщину. Але цей засіб не завжди ефективний, як було продемонстровано в 1988 році, коли B737, який експлуатується Aloha Airlines, мав дах першокласної кабіни відірвати. Цей літак мав пошкодження від корозії під напругою при ряді заклепок у зрощеннях колін фюзеляжу, і це дозволило множинним дрібним тріщинам зв'язатися, утворюючи велику тріщину. Велика увага в даний час спрямована на захист від такого роду «багатосайтових пошкоджень».

Важливо усвідомлювати, що критична довжина тріщини є абсолютним числом, що не залежить від розмірів конструкції, що містить її. Кожен раз, коли тріщина стрибає вперед, скажімо\(\delta a\), з невеликим приростом, з щойно розвантаженого матеріалу біля тріщини виділяється додаткова кількість енергії деформації. Знову використовуючи нашу спрощену картину області трикутної форми, яка знаходиться під нульовим напруженням, тоді як решта структури продовжує відчувати загальне прикладене напруження, на малюнку 3 легко побачити, що набагато більше енергії виділяється через стрибок у положенні 2, ніж у положенні 1. Це ще одна причина, чому дрібні речі, як правило, сильніші: вони просто недостатньо великі, щоб містити критичну довжину тріщини.

Приклад\(\PageIndex{2}\)
Гордон (J.E. Gordon, Structures, або Чому речі не падають, Пленум, Нью-Йорк, 1978.) розповідає про кухаря корабля, який одного разу помітив тріщину в сталевій палубі його камбузу. Його начальство запевнило його, що турбуватися нема про що - тріщина, безумовно, була невеликою порівняно з величезною основною масою корабля - але кухар почав малювати дати на підлозі, щоб позначити нову довжину тріщини щоразу, коли бій грубої погоди призведе до того, що вона росте довше. З кожним просуванням тріщини додатковий настильний матеріал розвантажувався, і раніше містилася в ньому енергія деформації виділялася. Але оскільки кількість енергії, що виділяється, зростає квадратично з довжиною тріщини, в кінцевому підсумку було достатньо, щоб зберегти тріщину зростанням навіть без подальшого збільшення валового навантаження. Коли це сталося, корабель розбився на дві частини; це здається дивним, але є більше, ніж кілька таких випадків, які дуже добре задокументовані. Як це сталося, частина корабля з відмітками, що показують зростання тріщини, була врятована, і це стало одним з найкращих задокументованих прикладів повільного зростання тріщини з подальшим остаточним катастрофічним руйнуванням.
Калібрування відповідності
Доступний ряд засобів, за допомогою яких\(\mathcal{G}_c\) можна виміряти властивість матеріалу. Одна з них відома як калібрування відповідності, яка використовує концепцію відповідності як відношення деформації до прикладеного навантаження:\(C = \delta/P\). Загальна енергія деформації\(U\) може бути записана з точки зору цієї відповідності як:
\(U = \dfrac{1}{2} P \delta = \dfrac{1}{2} CP^2\)

Відповідність відповідного зразка, наприклад консольного бруса, може бути виміряна експериментально як функція довжини a тріщини, яка вирощена в зразок (див. Рис. Швидкість вивільнення енергії деформації потім може бути визначена шляхом диференціації кривої відповідності від довжини:
\[\mathcal{G} = \dfrac{\partial U}{\partial a} = \dfrac{1}{2} P^2 \dfrac{\partial C}{\partial a}\]
Потім критичне значення знаходять шляхом вимірювання критичного навантаження\(\mathcal{G}\)\(\mathcal{G}_c\),\(P_c\) необхідного для руйнування зразка, що містить тріщину довжини\(a_c\), і використовуючи нахил кривої відповідності при цьому ж значенні\(a\):
\[\mathcal{G}_c = \dfrac{1}{2}P_c^2 \dfrac{\partial C}{\partial a} |_{a = a_c}\]
Приклад\(\PageIndex{3}\)
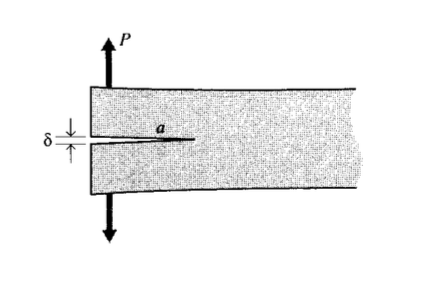
Для зразка подвійної консольної балки (DCB), такого як показано на малюнку 5, теорія променя дає відхилення як
\(\dfrac{\delta}{2} = \dfrac{Pa^3}{3EI}\)
де\(I = bh^3/12\). Еластична відповідність тоді
\(C = \dfrac{\delta}{P} = \dfrac{2a^3}{3EI}\)
Якщо тріщина спостерігається, щоб стрибати вперед\(P = P_c\), коли, Рівняння 3 може бути використано для обчислення критичної швидкості викиду енергії деформації як
\(\mathcal{G}_c = \dfrac{1}{2} P_c^2 \cdot \dfrac{2a^3}{EI} = \dfrac{12P_c^2 a^2}{b^2h^3E}\)
Підхід інтенсивності стресу
У той час як підхід енергетичного балансу забезпечує багато розуміння процесу руйнування, альтернативний метод, який досліджує напружений стан біля кінчика гострої тріщини безпосередньо виявився більш корисним в інженерній практиці. У літературі розглядаються три типи тріщин, які називаються режимами I, II та III, як показано на малюнку 6. Режим I - це режим нормального відкриття, який ми підкреслимо тут, тоді як режими II та III - це режими ковзання зсуву. Як було викладено в Модулі 16, напіваверсний метод, розроблений Вестергаардом, показує, що напруження режиму відкриття мають бути:
\[\begin{array} {c} {\sigma_x = \dfrac{K_I}{\sqrt{2\pi r}} \cos \dfrac{\theta}{2} (1 - \sin \dfrac{\theta}{2} \sin \dfrac{3 \theta}{2}) + \dots} \\ {\sigma_y = \dfrac{K_I}{\sqrt{2\pi r}} \cos \dfrac{\theta}{2} (1 + \sin \dfrac{\theta}{2} \sin \dfrac{3 \theta}{2}) + \dots} \\ {\tau_{xy} = \dfrac{K_I}{\sqrt{2\pi r}} \cos \dfrac{\theta}{2} \cos \dfrac{3\theta}{2} \sin \dfrac{\theta}{2} \cdots} \end{array}\]
Для відстаней, близьких до кінчика тріщини\((r\le 0.1a)\), терміни другого та вищого порядку, позначені точками, можуть бути нехтовані. На великих відстанях від верхівки тріщини ці відносини припиняють застосовуватися і напруження наближаються до своїх величин далекого поля, які б отримали, якби тріщина не була присутня.

\(KI\)У Eqns. 6.4.4 є дуже важливим параметром, відомим як коефіцієнт інтенсивності напруги. I індекс використовується для позначення режиму відкриття тріщини, але аналогічні відносини застосовуються в режимах II і III. Рівняння показують три фактори, які разом зображують напружений стан біля кінчика тріщини: коефіцієнт знаменника\((2\pi r)^{-1/2}\) показує сингулярний характер розподілу напружень;\(\sigma\) наближається до нескінченності, коли наближається кінчик тріщини, із\(r^{-1/2}\) залежністю. Кутова залежність відокремлюється як інший фактор: наприклад\(f_x = \cos \theta/2 \cdot (1 - \sin \theta/2 \sin 3\theta/2) + \cdots\). Коефіцієнт\(K_I\) містить залежність від прикладеного напруження\(\sigma_{\infty}\)\(a\), довжини тріщини та геометрії зразка. \(KI\)Фактор дає загальну інтенсивність розподілу напружень, звідси і його назва.
Для конкретного випадку центральної тріщини ширини\(2a\) або крайової тріщини довжиною\(2a\) у великому аркуші\(K_I = \sigma_{\infty} \sqrt{\pi a}\), а\(K_I = 1.12 \sigma_{\infty} \sqrt{\pi a}\) для крайової тріщини довжиною\(2a\) у великому листі. (Коефіцієнт, очевидно,\(\pi\) може бути скасований\(\pi\) за допомогою знаменника Рівняння 6.4.4, але зазвичай зберігається для узгодженості з попередньою роботою.) Вирази\(K_I\) для деяких додаткових геометрій наведені в таблиці 1. Література містить вирази\(K\) для великої кількості тріщин і геометрій навантаження, і існують як числові, так і експериментальні процедури для визначення коефіцієнта інтенсивності напружень конкретної фактичної геометрії.
| Тип тріщини | Фактор інтенсивності стресу,\(K_I\) |
| Центральна тріщина, довжина\(2a\), в нескінченній пластині | \(\sigma_{\infty} \sqrt{\pi a}\) |
| Край тріщини, довжиною\(a\), в напівнескінченну пластину | \(1.12 \sigma_{\infty} \sqrt{\pi a}\) |
| Центральна тріщина у формі пеніка, радіус\(a\), в нескінченному тілі | \(2 \sigma_{\infty} \sqrt{\tfrac{a}{\pi}}\) |
| Центральна тріщина, довжина\(2a\) в плиті ширини\(W\) | \(\sigma_{\infty} \sqrt{W \tan (\tfrac{\pi a}{W})}\) |
| 2 симетричні крайові тріщини, кожна довжина\(a\), в пластині загальної ширини\(W\) | \(\sigma_{\infty} \sqrt{W[\tan (\tfrac{\pi a}{W}) + 0.1 \sin (\dfrac{2 \pi a}{W})]}\) |
Ці фактори інтенсивності напружень використовуються при проектуванні та аналізі, стверджуючи, що матеріал може витримувати напруження наконечника тріщин до критичного значення інтенсивності напружень\(K_{Ic}\), що називається, за межами якого тріщина швидко поширюється. Цей критичний коефіцієнт інтенсивності напружень тоді є мірою в'язкості матеріалу. Потім напруга\(\sigma_f\) руйнування пов'язана з довжиною тріщини a та в'язкістю руйнування
\[\sigma_f = \dfrac{K_{Ic}}{\alpha \sqrt{\pi a}}\]
де\(\alpha\) - геометричний параметр, рівний 1 для крайових тріщин і, як правило, порядку одиниці для інших ситуацій. Вирази для α підсумовуються для широкого спектру геометрій зразків та тріщин, а спеціальні методи скінченних елементів доступні для обчислення його для нових ситуацій.
Інтенсивність стресу та точки зору енергії взаємопов'язані, що можна побачити, порівнюючи Eqns. 6.4.1 та 6.4.5 (з\(\alpha = 1\)):
\(\sigma_f = \sqrt{\dfrac{E\mathcal{G}_c}{\pi a}} = \dfrac{K_{Ic}}{\sqrt{\pi a}} \to K_{Ic}^2 = E \mathcal{G}_c\)
Це співвідношення застосовується при плоскому напруженні; воно дещо відрізняється в площині деформації:
Для металів з\(v = .3\),\((1 - v^2) = 0.91\). Це не велика зміна; однак числові значення\(\mathcal{G}_c\) або сильно\(K_{Ic}\) відрізняються в плоских напруженнях або плоских деформаційних ситуаціях, як буде описано нижче.
Типові значення\(G_{Ic}\) та\(K_{Ic}\) для різних матеріалів наведені в таблиці 2, і видно, що вони варіюються в дуже широкому діапазоні від матеріалу до матеріалу. Деякі полімери можуть бути дуже жорсткими, особливо при оцінці на фунтові основи, але сталеві сплави важко перемогти з точки зору абсолютної стійкості до поширення тріщин.
| Матеріал | \(G_{Ic} (kJm^{-2})\) | \(K_{Ic}(MNm^2)\) | \(E(GPa)\) |
|---|---|---|---|
| Сталевий сплав | \ (G_ {Ic} (KJM^ {-2})\)» клас = "lt-eng-44553">107 | \ (K_ {Ic} (Мнм ^ 2)\)» клас = "lt-eng-44553">150 | \ (E (ГПа)\)» клас = «lt-eng-44553">210 |
| Алюмінієвий сплав | \ (G_ {Ic} (KJM^ {-2})\)» клас = "lt-eng-44553">20 | \ (K_ {Ic} (Мнм ^ 2)\)» клас = "lt-eng-44553">37 | \ (E (ГПа)\)» клас = «lt-eng-44553">69 |
| Поліетилен | \ (G_ {Ic} (KJM^ {-2})\)» клас = "lt-eng-44553">20 (\(J_{Ic}\)) | \ (K_ {Ic} (Мнм ^ 2)\)» клас = "lt-eng-44553">- | \ (E (ГПа)\)» клас = «lt-eng-44553">0,15 |
| Ударостійкий полістирол | \ (G_ {Ic} (KJM^ {-2})\)» клас = "lt-eng-44553">15.8 (\(J_{Ic}\)) | \ (K_ {Ic} (Мнм ^ 2)\)» клас = "lt-eng-44553">- | \ (E (ГПа)\)» клас = «lt-eng-44553">2.1 |
| Сталь - м'яка | \ (G_ {Ic} (KJM^ {-2})\)» клас = "lt-eng-44553">12 | \ (K_ {Ic} (Мнм ^ 2)\)» клас = "lt-eng-44553">50 | \ (E (ГПа)\)» клас = «lt-eng-44553">210 |
| Гума | \ (G_ {Ic} (KJM^ {-2})\)» клас = "lt-eng-44553">13 | \ (K_ {Ic} (Мнм ^ 2)\)» клас = "lt-eng-44553">- | \ (E (ГПа)\)» клас = «lt-eng-44553">0,001 |
| Термосет, армований скловолокном | \ (G_ {Ic} (KJM^ {-2})\)» клас = "lt-eng-44553">7 | \ (K_ {Ic} (Мнм ^ 2)\)» клас = "lt-eng-44553">7 | \ (E (ГПа)\)» клас = «lt-eng-44553">7 |
| Загартована гумою епоксидна смола | \ (G_ {Ic} (KJM^ {-2})\)» клас = "lt-eng-44553">2 | \ (K_ {Ic} (Мнм ^ 2)\)» клас = "lt-eng-44553">2.2 | \ (E (ГПа)\)» клас = «lt-eng-44553">2.4 |
| ПММА | \ (G_ {Ic} (KJM^ {-2})\)» клас = "lt-eng-44553">0.5 | \ (K_ {Ic} (Мнм ^ 2)\)» клас = "lt-eng-44553">1.1 | \ (E (ГПа)\)» клас = «lt-eng-44553">2.5 |
| Полістирол | \ (G_ {Ic} (KJM^ {-2})\)» клас = "lt-eng-44553">0.4 | \ (K_ {Ic} (Мнм ^ 2)\)» клас = "lt-eng-44553">1.1 | \ (E (ГПа)\)» клас = «lt-eng-44553">3 |
| Деревина | \ (G_ {Ic} (KJM^ {-2})\)» клас = "lt-eng-44553">0.12 | \ (K_ {Ic} (Мнм ^ 2)\)» клас = "lt-eng-44553">0.5 | \ (E (ГПа)\)» клас = «lt-eng-44553">2.1 |
| Скло | \ (G_ {Ic} (KJM^ {-2})\)» клас = «lt-eng-44553">0.007 | \ (K_ {Ic} (Мнм ^ 2)\)» клас = "lt-eng-44553">0.7 | \ (E (ГПа)\)» клас = «lt-eng-44553">70 |
Приклад\(\PageIndex{4}\)
Рівняння 6.4.5 забезпечує розрахункове співвідношення між\(\sigma\) прикладеною напругою\(K_{Ic}\), в'язкістю матеріалу та довжиною тріщини\(a\). Будь-який з цих параметрів можна обчислити після того, як відомі два інших. Щоб проілюструвати одне застосування процесу, скажімо, ми хочемо визначити безпечний робочий тиск у алюмінієвому посудині під тиском діаметром 0,25 м та товщиною стінки 5 мм. Спочатку припускаючи відмову за плинністю, коли напруга обруча досягає межі текучості (330 МПа) і використовуючи коефіцієнт запасу міцності 0,75, ми можемо обчислити максимальний тиск як
\(p = \dfrac{0.75 \sigma t}{r} = \dfrac{0.75 \times 330 \times 10^6}{0.25/2} = 9.9\text{ MPa} = 1400\text{ psi}\)
Щоб застрахуватися від руйнування шляхом швидкого зростання тріщин, тепер обчислюємо максимальну довжину тріщини, допустиму при робочому напруженні, використовуючи значення ударної в'язкості\(K_{Ic} = 41 \text{ MPa} \sqrt{m}\):
\(a = \dfrac{K_{Ic}^2}{\pi \sigma^2} = \dfrac{(41 \times 10^6)^2}{\pi (0.75 \times 330 \times 10^6)^2} = 0.01\ m = 0.4\ in\)
Тут\(\alpha = 1\) передбачалася крайова тріщина з. Повинен бути реалізований графік перевірки, який здатний виявити тріщини до того, як вони досягнуть такого розміру.
Ефект геометрії зразка

Міцність або стійкість до росту тріщин матеріалу регулюється енергією, що поглинається, коли тріщина рухається вперед. У надзвичайно крихкому матеріалі, такому як віконне скло, ця енергія в першу чергу полягає в розриві хімічних зв'язків вздовж площини тріщини. Але, як уже згадувалося, у більш жорстких матеріалах розрив зв'язку відіграє відносно невелику роль у протистоянні зростанню тріщин, причому, безумовно, найбільша частина енергії руйнування пов'язана з пластичним потоком біля кінчика тріщини. Біля наконечника тріщини присутня «пластична зона», всередині якої напруги, передбачені рівнянням 6.4.4, були б вище межі текучості матеріалу\(\sigma_Y\). Оскільки напруга не може піднятися вище\(\sigma_Y\), напруга в цій зоні є\(\sigma_Y\) скоріше, ніж напругою, заданою рівнянням 6.4.4. До першого наближення відстань rp цієї зони простягається вздовж\(x\) -осі можна знайти за допомогою Рівняння 6.4.4 з,\(\theta = 0\) щоб знайти відстань, на якій напруга кінчика тріщини зменшується до\(\sigma_Y\):
\(\sigma_y = \sigma_Y = \dfrac{K_I}{\sqrt{2\pi r_p}}\)
\[r_p = \dfrac{K_I^2}{2 \pi \sigma_Y^2\]
Це співвідношення проілюстровано на малюнку 7. Оскільки інтенсивність напруги збільшується або за рахунок підвищення накладеного напруги, або за рахунок подовження тріщин, розмір пластикової зони також збільшиться. Але ступінь пластичного потоку в кінцевому підсумку обмежується молекулярною або мікроструктурною рухливістю матеріалу, і зона може стати лише такою великою. Коли зона не може рости більше, тріщина більше не може бути обмежена і відбувається нестабільне поширення. Значення,\(K_I\) при якому це відбувається, потім можна вважати властивістю матеріалу, названим\(K_{Ic}\).
Для того,\(K_{Ic}\) щоб виміряне значення було дійсним, розмір пластичної зони не повинен бути таким великим, щоб взаємодіяти з вільними межами зразка або руйнувати основний характер сингулярного розподілу напружень. Специфікація ASTM для випробування на в'язкість на руйнування (E 399-83, «Стандартний метод випробувань для в'язкості руйнування плоских деформацій металевих матеріалів», ASTM, 1983.) визначає геометрію зразка, щоб гарантувати, що зразок великий порівняно з довжиною тріщини та розміром пластичної зони (див. Рис. 8):
Малюнок 8: Розміри зразка в'язкості руйнування.
Велика увага була приділена важливому випадку, в якому існує достатня пластичність, щоб унеможливити задоволення вищезазначених критеріїв. У цих випадках слід відмовитися від перегляду інтенсивності напружень, а замість них використовуються альтернативні методи, такі як J-інтеграл або метод зміщення розкриття наконечника тріщини. Для обговорення цих підходів читач звертається до посилань, перерахованих в кінці модуля.

В'язкість руйнування, виміряна\(K_c\) або, по суті,\(\mathcal{G}_c\) є мірою ступеня пластичної деформації, пов'язаної з розширенням тріщини. Очікується, що кількість пластичного потоку буде масштабуватися лінійно з товщиною зразка, оскільки зменшення товщини наполовину, природно, зменшить обсяг пластично деформованого матеріалу приблизно навпіл. Тому в'язкість зростає лінійно, принаймні спочатку, з товщиною зразка, як показано на малюнку 9. Зрештою, однак, спостерігається міцність, щоб пройти максимум і після цього впасти до нижчого значення. Ця втрата в'язкості понад певну критичну товщину надзвичайно\(t^*\) важлива в конструкції проти руйнування, оскільки використання занадто тонкого зразка для вимірювання в'язкості дасть нереально оптимістичне значення для\(\mathcal{G}_C\). Вимоги до розміру зразка для дійсного випробування на в'язкість руйнування такі, що вимірюється найбільш консервативне значення.
Критична товщина полягає в тому, що призводить до того, що зразок переважає стан плоского деформації, на відміну від плоского напруження. Напруга в\(z\) напрямку наскрізної товщини повинна стати нульовою з боків зразка, оскільки там не застосовується тяга, і в тонкому зразку напруга не матиме місця для підняття до помітних значень всередині матеріалу. Штам у\(z\) напрямку, звичайно, не дорівнює нулю, і зразок зазнає скорочення Пуассона, дане\(\epsilon_z = v(\sigma_x + \sigma_y)\). Але коли зразок товщі, матеріал поблизу центру не зможе стиснутися збоку через обмеження сусіднього матеріалу. Тепер деформація\(z\) -direction дорівнює нулю, тому напруга розтягування виникне, коли матеріал намагається стиснутися, але йому не дозволяється це робити. Значення σ z піднімається з нуля на зовнішній поверхні і наближається до максимального значення, заданого\(\sigma_z \approx v(\sigma_x + \sigma_y)\) на відстані,\(t^*\) як показано на малюнку 10. Щоб гарантувати, що умови плоского деформації домінують, товщина зразка\(t\) повинна бути такою, що\(t \gg 2t^*\).
Тривісний напружений стан, встановлений поблизу центру товстого зразка поблизу кінчика тріщини, зменшує максимальне напруження зсуву, доступне для приводу пластичного потоку, оскільки максимальне напруження зсуву дорівнює половині різниці найбільшого та найменшого основного напруження, а найменший тепер більше нуля. Або еквівалентно можна констатувати, що рухливість матеріалу обмежується неможливістю укладати контракти в латеральному порядку. З точки зору стресу або деформації ступінь доступної пластичності зменшується, роблячи зразок товстим.
Приклад\(\PageIndex{5}\)
Розміри пластичних зон для випадків плоского напруження та плоского деформації можуть бути візуалізовані за допомогою відповідного критерію плинності разом із виразами для напруги біля кінчика тріщини. Критерій плинності v. Мізеса наведено в розрізі головних напружень у модулі 20 як
Основні напруги можна отримати з Eqns. 6.4.4 як
\(\sigma_1 = \dfrac{K_I}{\sqrt{2 \pi r}} \cos \dfrac{\theta}{2} (1 + \sin \dfrac{\theta}{2})\)
Третій основний наголос:
\(\sigma_3 = \begin{cases} 0, \text{ plane stress} \\ v(\sigma_1 + \sigma_2), \text{ plane strain} \end{cases}\)
Ці напруги можна підставити в критерій плинності, який потім вирішується для радіуса,\(r\) при якому відбувається вихід. Цей радіус зручно нормалізувати радіусом пластичної зони вздовж\(x\) −осі, заданого рівнянням 6.4.6. Команди Maple для виконання цих замін і побудови результату є:
# Радіус пластичної зони вздовж осі x> rp: = K [I] ^2/ (2* Pi* Sigma [Y] ^2):
# v. Критерій виходу Мізеса через основні
напруження> v_mises: =2*сигма [Y] ^2= (сигма [1] -сигма [2]) ^2 + (сигма [1] -сигма [3]) ^2 + (сигма [2] -сигма [3]) ^2:
# Основні напруги в області
тріщини> сигма [1]: =( K [I] /sqrt (2*Pi*R)) *cos (тета/2) * (1+грін (тета/2)):
> сигма [2]: =( K [I] /sqrt (2*pi*r)) * cos (тета/2) * (1-sin (тета/2));
# Оцініть проти Мізеса для плоского напруження (v_strs) та плоского деформації (v_strn) # Візьміть nu = 0,3
> v_strs: =subs (сигма [3] =0, v_mises):
> v_strn: =sigma (сигма [3] =.3* (сигма [1] +сигма [2]), v_mises):
# Вирішити для радіуса пластичної зони, нормалізувати rp
# pl_strs для плоского випадку напруги, pl_strn для плоского деформації> pl_strs: = вирішити (v_strs, r) /rp:
> pl_strn: =solve (v_strn, r) /rp:
# Ділянка нормованих пластичних зон для плоских напружень і плоских деформацій > ділянка ({pl_strs, pl_strn}, theta=0.. 2*Pi, coords=polar);

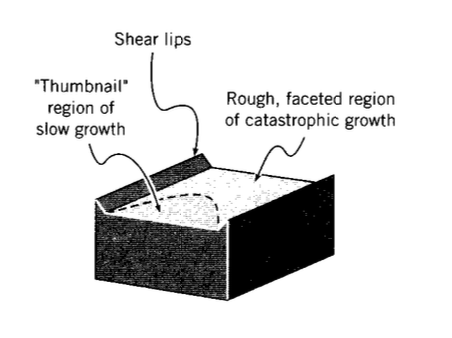
Навіть у товстому зразку напруга в напрямку z повинна наближатися до нуля на бічних поверхнях. Таким чином, області біля поверхні вільні від тривісного обмеження напруги і демонструють більший пластичний потік, керований зсувом. Після того, як тріснутий зразок був випробуваний на відмову, плоский малюнок «мініатюри» часто буде видно, як показано на малюнку 12. Це область повільного зростання тріщини, де тріщина здатна зберігати свою бажану орієнтацію поперечно напруженню у напрямку. Зростання тріщини біля країв затримується додатковим пластичним потоком там, тому лінія тріщини схиляється всередину. Коли напруга збільшується достатньо, щоб призвести до катастрофічного зростання тріщини, вона, як правило, робить це на досить високих швидкостях, щоб поперечна орієнтація не завжди підтримувалася. Область швидкого руйнування, таким чином, гранована і груба, що призводить до деякої механіки заднього двору стверджувати, що матеріал не вдалося, оскільки він «кристалізувався».
По краях зразка часто можна зустріти «зсувні губи», на яких тріщина розвинулася струмом зсуву і при інтенсивній пластичній деформації. Губи будуть близько 45\(^{\circ}\) кута, орієнтація максимальних площин зсуву.
Розмір зерна і температура
Сталь є настільки важливим і широко використовуваним конструкційним матеріалом, що легко забути, що сталь - досить недавнє технологічне нововведення. У дев'ятнадцятому столітті дерево було домінуючим матеріалом для багатьох мостів, будівель та кораблів. Оскільки використання чавуну і сталі набуло більшого поширення в другій половині того ж століття і першій частині теперішнього, відбувся ряд катастроф, які можна простежити до тодішнього неповного стану розуміння цих матеріалів, особливо щодо їх схильності ставати крихкими при низькому рівні. температури. Багато з цих невдач були описані та проаналізовані у захоплюючій книзі Паркера (Е.Р. Паркер, Крихка поведінка інженерних споруд, John Wiley & Sons, 1957).
Однією з таких крихких невдач є, мабуть, найвідоміша катастрофа останніх кількох століть, занурення трансатлантичного океану лайнера «Титанік» 15 квітня 1912 року з втратою близько 1500 чоловік і лише 705 вижили. Ще зовсім недавно вважалося, що трагедія викликана довгим гасом, прорваним через корпус корабля айсбергом. Однак, коли уламки корабля були остаточно виявлені в 1985 році за допомогою підводних роботів, ніяких доказів такого гашу виявлено не було. Далі роботи пізніше змогли повернути зразки корабельної сталі, аналіз яких породив альтернативне пояснення.
Зараз добре відомо, що менші марки стали, особливо ті, що мають великі концентрації домішок, таких як міжстильні вуглецеві включення, схильні до крихкості при низьких температурах. Вільям Гарцке, військово-морський архітектор з нью-йоркською фірмою Gibbs & Cox, і його колеги стверджували, що сталь в «Титаніку» дійсно крихка в 31\(^{\circ}F\) водах Атлантики тієї ночі, і що 22-вузлове зіткнення з айсбергом породило не гаш, а велике розтріскування яка вода могла потрапити в корпус. Якби сталь залишалася жорсткою при такій температурі, ці автори вважають, що розтріскування, можливо, було набагато менш великим. Це уповільнило б повені і дозволило б більше часу для рятувальних суден, щоб дістатися до місця події, що могло б значно збільшити кількість тих, хто вижив.

У перехідних металах ОЦК, таких як залізо та вуглецева сталь, крихке руйнування може бути ініційоване дислокаційним ковзанням всередині кристалічного зерна. Ковзання відбувається при межі текучості\(\sigma_Y\), який змінюється залежно від розміру зерна відповідно до закону Холла-Петча, як описано в Модулі 21:
\(\sigma_Y = \sigma_0 + k_Y d^{-1/2}\)
Дислокації не здатні поширюватися за межі зерна, оскільки сусідні зерна взагалі не матимуть своїх площин ковзання належним чином орієнтованих. Потім дислокації «накопичуються» проти кордонів зерен, як показано на малюнку 13. Скупка дислокації діє аналогічно внутрішній тріщині довжиною, яка лущиться з розміром зерна d, посилюючи напругу в навколишніх зернятках. Замінюючи a by\(d\) у модифікованому рівнянні Гріффіта (Рівняння 6.4.1), прикладене напруження, необхідне для спричинення руйнування сусідніх зерен, пов'язане з розміром зерен як
\(\sigma_f = k_f d^{-1/2}, k_f \propto \sqrt{\dfrac{E\mathcal{G}_c}{\pi}}\)
Наведені вище два співвідношення для врожайності та руйнування побудовані на малюнку 14 проти зворотного розміру зерна кореня (так розмір зерен збільшується вліво), при цьому нахили є\(k_Y\) і\(k_f\) відповідно. Коли\(k_f > k_Y\), перелом не відбудеться, поки\(\sigma = \sigma_Y\) для значень d зліва від точки\(A\), оскільки врожайність і ковзання є обов'язковою умовою для розщеплення. У цьому регіоні напруження врожайності та руйнування однакові, а руйнування виглядає крихким, оскільки великомасштабна врожайність не матиме шансів статися. Праворуч від точки відбувається врожайність до руйнування\(A\), і матеріал виглядає пластичним. \(A\)Тому точка визначає критичний розмір зерна,\(d^*\) при якому відбудеться перехід «ніль-пластичність» від пластичного (зерна менше\(d^*\)) до крихкого руйнування.
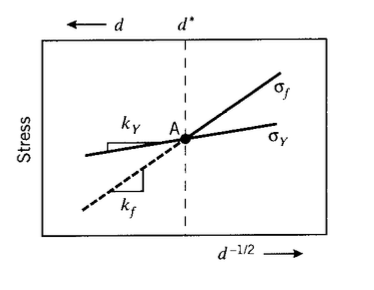
При зниженні температури напруга плинності σ Y буде збільшуватися, як описано в модулі 20, а напруга руйнування σ f зменшиться (оскільки атомна рухливість і, таким чином,\(\mathcal{G}_C\) зменшиться). Тому точка\(A\) зміщується вправо при зниженні температури. Критичний розмір зерна для нульової пластичності тепер відбувається при меншому значенні; тобто зерна повинні бути меншими, щоб уникнути крихкості матеріалу. Аналогічно, рафінування розміру зерна має ефект зниження температури пластично-крихкого переходу. Отже, подрібнення розміру зерна підвищує як урожайність, так і напруження руйнування, знижує температуру пластично-крихкого переходу, а також сприяє в'язкості. Це надзвичайно корисний механізм зміцнення, оскільки інші методи, такі як деформаційне зміцнення та твердіння твердим розчином, мають тенденцію до посилення за рахунок ударної в'язкості.
Інші фактори, крім температури, також можуть покришити сталь. Включення, такі як вуглець і фосфор, діють на іммобілізацію систем ковзання, які в іншому випадку можуть зняти стреси, пов'язані з дислокацією скупчення, і ці включення можуть помітно підвищити напругу текучості і, таким чином, пластично-крихку температуру переходу. Подібні ефекти можуть бути викликані пошкодженням від високоенергетичного випромінювання, тому крихкість компонентів ядерного реактора викликає велике занепокоєння. Крихкості також сприяє наявність насічок, так як вони генерують тривісні напруги, які стримують пластичний потік. Високі швидкості деформації сприяють крихкості, оскільки напруга потоку, необхідна для розміщення швидкості деформації, вище, а неправильне зварювання може призвести до крихкості як шляхом зміни мікроструктури сталі, так і шляхом створення залишкових внутрішніх напружень.
Загальні посилання
- Андерсон, Т.Л., Механіка руйнувань: Основи та застосування, CRC Press, Бока-Ратон, 1991.
- Barsom, J.M., ред., Ретроспектива механіки руйнувань, Американське товариство випробувань та матеріалів, Філадельфія, 1987.
- Коллінз, Дж. А., Відмова матеріалів в механічному дизайні, Wiley, 1981.
- Кортні, Т.Х., Механічна поведінка матеріалів, Макгроу-Хілл, Нью-Йорк, 1990.
- Гордон, Дж. Е., Нова наука про міцні матеріали, або Чому ви не падаєте через підлогу, Princeton University Press, 1976.
- Герцберг, Р.В., Механіка деформації та руйнування інженерних матеріалів, Вілі, Нью-Йорк, 1976.
- Нотт, Дж. Ф., Основи механіки руйнувань, Джон Вілі - Холстед Прес, Нью-Йорк, 1973.
- Менденхолл, В., Р.Л. Шеффер і Д.Д. Wackerly, Математична статистика з додатками, Даксбері Прес, Бостон, 1986.
- Стролі, JE, і В.Ф. Браун, Випробування на в'язкість руйнування, ASTM STP 381, 133, 1965.
- 1967.
Вправа\(\PageIndex{1}\)
Використовуючи розробку, аналогічну тій, яка використовується в модулі 21 для теоретичного напруження плинності, показати, що теоретична гранична міцність на розрив є\(\sigma^{th} \approx E/10\) (набагато більшою, ніж спостерігається експериментально). Припустимо гармонічну функцію атомної сили\(\sigma = \sigma^{th} \sin(2\pi x/\lambda\)), де\(x\) є зміщення атома з положення рівноваги і\(\lambda \approx a_0\) є міжатомним інтервалом. Максимальний стрес потім\(\sigma^{th}\) можна знайти, використовуючи
\(E = (\dfrac{d \sigma}{d\epsilon})_{x \to 0} \text{ and } \epsilon = \dfrac{x}{a_0}\)
Вправа\(\PageIndex{2}\)
Використовуючи коефіцієнт запасу міцності 2, знайдіть безпечний робочий тиск у закритому сталевому посудині під тиском\(1'\) у діаметрі та товщині\(0.2''\) стінки.
Вправа\(\PageIndex{3}\)
Посудина під тиском будується діаметром\(d = 18''\) і довжиною\(L = 6'\). Посудина повинна бути здатна витримувати внутрішній тиск\(p = 1000\text{ psi}\), а товщина стінки така, щоб тримати номінальне напруження обруча під\(2500\text{ psi}\). Однак посудина лопається лише під внутрішнім тиском\(500\text{ psi}\), і мікрографічне дослідження виявляє, що перелом був ініційований внутрішньою тріщиною\(0.1''\) в довжину. Обчисліть в'язкість руйнування (\(K_{Ic}\)) матеріалу.
Вправа\(\PageIndex{4}\)
Високо зшита епоксидна смола має коефіцієнт лінійного теплового розширення\(\alpha = 5 \times 10^{-5} K^{-1}\)\(G_{IC} = 120 J/m^2\),\(E = 3.2 GPa\),, і\(v = 0.35\). Товстий шар смоли затвердіє і міцно скріплюється з алюмінієвою частиною (\(\alpha = 2.5 \times 10^{-5} K^{-1}\)) при\(180^{\circ} C\). Обчисліть мінімальний розмір дефекту, необхідний для ініціювання розтріскування в смолі при охолодженні до\(20^{\circ} C\). Візьміть\(\alpha\) в рівнянні 6.4.5, щоб бути\(2/\pi\) для копієчкових тріщин радіусом\(a\) в широкому аркуші.
Вправа\(\PageIndex{5}\)
(а) Товста пластина з алюмінієвого сплаву шириною 175 мм містить центрально-розташовану тріщину довжиною 75 мм. Пластина відчуває крихке руйнування при прикладеному напруженні (одноосному, поперечному до тріщини) 110 МПа. Визначте в'язкість руйнування матеріалу.
(b) Яким було б напруження руйнування, якби пластина була достатньо широкою, щоб дозволити припущення нескінченної ширини?
Вправа\(\PageIndex{6}\)
Для того, щоб отримати дійсні жорсткості плоского деформації, розмір пластичної зони повинен бути невеликим щодо товщини зразка\(B\)\(a\), довжини тріщини та ширини «зв'язки»\(W - a\). Встановленим критерієм є
Ранжируйте матеріали в базі даних за параметром, зазначеним у правій частині цього виразу.
Вправа\(\PageIndex{7}\)
Коли навантаження 150 кН прикладається до розтяжного зразка, що містить тріщину 35 мм, загальний зміщення між кінцями зразка становить 0,5 мм. Коли тріщина виросла до 37 мм, зміщення для цієї ж навантаження становить 0,505 мм. Екземпляр товщиною 40 м. Навантаження на руйнування ідентичного зразка, але при довжині тріщини 36 мм, становить 175 кН. Знайдіть в'язкість матеріалу\(K_{Ic}\) на руйнування.
