5.4: Лінійна в'язкоеластичність
- Page ID
- 30722
1. Вступ
Цей документ покликаний окреслити важливий аспект механічної реакції полімерів та полімерно-матричних композитів: поле лінійної в'язкопружності. Теми, включені тут, спрямовані на надання навчального вступу до цього великого та елегантного предмета, і не слід сприймати як ретельне або всебічне лікування. Для більш ретельного висвітлення слід ознайомитися з посиланнями, що з'являються або у вигляді виноски до тексту, або перераховані окремо в кінці приміток.
В'язкопружна реакція часто використовується як зонд в полімерній науці, оскільки він чутливий до хімії та мікроструктури матеріалу. Поняття та методи, представлені тут, важливі для цієї мети, але головною метою цього документа є продемонстрація того, як лінійна в'язкопружність може бути включена в загальну теорію механіки матеріалів, щоб конструкції, що містять в'язкопружні компоненти, можуть бути спроектовані та проаналізовано.
Хоча не всі полімери є в'язкопружними в будь-якій важливій практичній мірі, а ще менше - лінійно в'язкопружні (Огляд нелінійної в'язкопружної теорії див., наприклад, W.N. Findley et al., повзучість і релаксація нелінійних в'язкопружних матеріалів, Dover Publications, Нью-Йорк, 1989.), ця теорія забезпечує корисне інженерне наближення для багатьох застосувань у техніці полімерів та композитів. Навіть у випадках, що вимагають більш складних методів лікування, лінійна в'язкопружна теорія є корисною відправною точкою.
2. Молекулярні механізми
При впливі прикладеного напруження полімери можуть деформуватися будь-яким або обома принципово різними атомістичними механізмами. Довжини і кути хімічних зв'язків, що з'єднують атоми, можуть спотворюватися, переміщаючи атоми на нові позиції більшої внутрішньої енергії. Це невеликий рух і відбувається дуже швидко, вимагаючи всього\(\approx 10^{-12}\) секунд.
Якщо полімер має достатню молекулярну рухливість, можливі і більш масштабні перебудови атомів. Наприклад, відносно легке обертання навколо магістральних вуглецево-вуглецевих одиночних зв'язків може спричинити великі зміни в конформації молекули. Залежно від рухливості молекула полімеру може поширюватися в напрямку прикладеного напруги, що зменшує її конформаційну ентропію (молекула менш «невпорядкована»). Еластомери - гума - реагують майже повністю за допомогою цього ентропного механізму, з невеликим спотворенням їх ковалентних зв'язків або зміною їх внутрішньої енергії.
Поєднані перший і другий закони термодинаміки стверджують, як приріст механічної роботи,\(f\ dx\) виконаної над системою, може спричинити збільшення внутрішньої енергії\(dU\) або зниження ентропії\(dS\):
\[f\ dx = dU - T\ dS\]
Зрозуміло, що відносна важливість ентропного внеску зростає з температурою\(T\), і це забезпечує зручний засіб експериментального визначення жорсткості матеріалу в енергетичному або ентропному за походженням. Сила втягування, необхідна для утримання гумки при фіксованому подовженні, буде збільшуватися зі збільшенням температури, оскільки підвищене теплове збудження зробить внутрішню структуру більш енергійною в її природних спробах відновити хаотичність. Але сила втягування в розтягнутому сталевому зразку - який демонструє невелику ентропну еластичність - зменшуватиметься з температурою, оскільки теплове розширення буде діяти для зняття внутрішнього напруження.
На відміну від миттєвого характеру енергетично керованої пружності, кон-формаційні або ентропні зміни - це процеси, швидкість яких чутлива до локальної молекулярної рухливості. На цю рухливість впливають різні фізичні та хімічні фактори, такі як молекулярна архітектура, температура або наявність поглинених рідин, які можуть набухати полімер. Часто проста ментальна картина «вільного об'єму» - приблизно, простір, доступне для молекулярних сегментів, щоб діяти спільно, щоб здійснити рух або реакцію, про яку йде мова, - корисна для інтуїції цих швидкостей.
Ці швидкості конформаційних змін часто можуть бути описані з розумною точністю виразами типу Арреніуса форми
\[\text{rate} \propto \exp \dfrac{-E^\dagger}{RT}\]
де\(E^\dagger\) є очевидною енергією активації процесу і\(R = 8.314J/mol - ^{\circ}K\) є газова постійна. При температурах набагато вище «температури скляного переходу»,\(T_g\) позначеної на малюнку 1, швидкості настільки швидкі, щоб бути по суті миттєвими, і полімер діє гумовим способом, в якому він проявляє великі, миттєві та повністю оборотні деформації у відповідь на прикладене напруження.
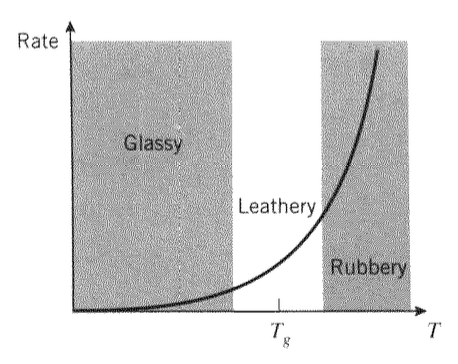
І навпаки, при температурах набагато менше\(T_g\), показники настільки повільні, що бути незначними. Тут процес розмотування ланцюга по суті «заморожений», тому полімер здатний реагувати тільки розтягуванням зв'язку. Тепер він реагує «склоподібним» чином, реагуючи миттєво і оборотно, але будучи нездатним бути напруженим за кілька відсотків перед розривом крихким чином.
У діапазоні поблизу\(T_g\) матеріал знаходиться посередині між склоподібним та гумовим режимами. Його реакцією є поєднання в'язкої плинності та еластичної твердості, і ця область називається «шкіряста», або, більш технічно, «в'язкопружна». Значення\(T_g\) є важливим дескриптором термомеханічної реакції полімеру і є фундаментальним показником схильності матеріалу до рухливості. Фактори, що підвищують рухливість, такі як поглинені розріджувачі, експансивні стресові стани та відсутність об'ємних молекулярних груп, все, як правило, виробляють більш низькі значення\(T_g\). Прозора полівінілбутиральна плівка, що використовується в автомобільних ламінатах лобового скла, є прикладом матеріалу, який використовується у в'язкопружному режимі, оскільки в'язкопружна реакція може бути джерелом значного розсіювання енергії під час удару.
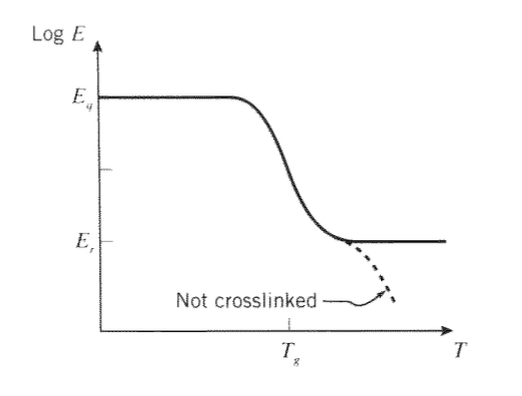
При температурах значно нижче\(T_g\), коли ентропні рухи заморожуються і можливі лише деформації пружних зв'язків, полімери проявляють відносно високий модуль пружності, званий «склоподібним модулем»\(E_g\), який знаходиться близько 3 ГПа (400 кпсі). У міру підвищення температури жорсткість різко падає, можливо, на два порядки, до значення, званого «модулем гуми»\(E_r\).\(T_g\) У еластомерів, які були постійно зшиті сіркою вулканізацією або іншими способами, значення значення\(E_r\) визначається насамперед щільністю зшивання; кінетична теорія пружності каучуку дає відношення як
\[\sigma = NRT (\lambda - \dfrac{1}{\lambda^2})\]
де\(\sigma\) - напруга,\(N\) - щільність зшивання (\(mol/m^3\)), і\(\lambda = L/L_0\) коефіцієнт розширення. Диференціація цього виразу дає нахил кривої напруження-деформації біля початку як\(E_r = 3NRT\).
Якщо матеріал не зшитий, жорсткість проявляє коротке плато через здатність молекулярних заплутань діяти як мережеві переходи; при ще більш високих температурах заплутування ковзає, і матеріал стає в'язкою рідиною. Ні склоподібний, ні гумовий модуль сильно не залежить від часу, але в безпосередній близькості від переходу близького\(T_g\) часу ефекти можуть бути дуже важливими. Зрозуміло, що графік модуля проти температури, як показано на малюнку 2, є життєво важливим інструментом у полімерному матеріалознавстві та техніці. Він надає карту життєво важливого інженерного властивості, а також є відбитком молекулярних рухів, доступних матеріалу.
3. Феноменологічні аспекти
Експериментально людина прагне охарактеризувати матеріали, виконуючи прості лабораторні випробування, з яких може бути отримана інформація, що стосується фактичних умов використання. У випадку з vis-coпружними матеріалами механічна характеристика часто складається з виконання одновісних випробувань на розтягнення, аналогічних тим, що використовуються для еластичних твердих тіл, але модифіковані таким чином, щоб забезпечити спостереження за часовою залежністю реакції матеріалу. Хоча було використано багато таких «в'язкопружних випробувань на розтяг», найчастіше зустрічаються лише три: повзучість, розслаблення напружень та динамічне (синусоїдальне) навантаження.
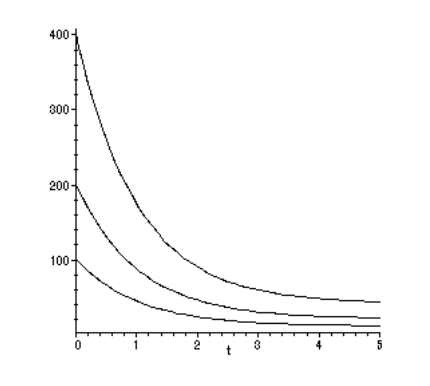
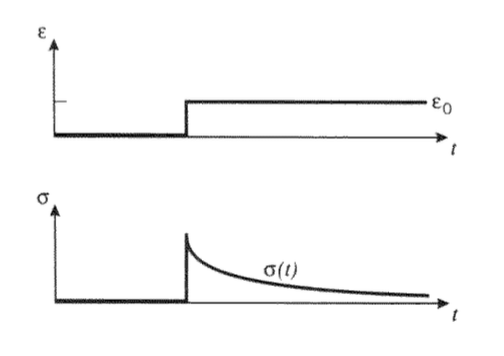
повзучість
Тест на повзучість складається з вимірювання залежної від часу деформації,\(\epsilon (t) = \delta (t)/L_0\) що виникає внаслідок застосування стійкого одновісного напруги\(\sigma_0\), як показано на малюнку 3. Ці три криві - це деформації, виміряні на трьох різних рівнях напруги, кожен з яких вдвічі перевищує величину попереднього.
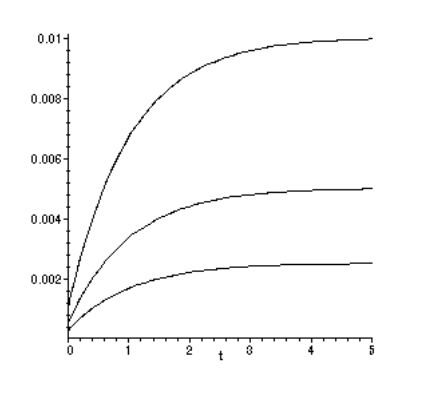
Зверніть увагу на малюнку 3, що коли напруга подвоюється, результуюча деформація подвоюється протягом усього періоду часу. Це відбувається, якщо матеріали лінійні за своєю реакцією. Якщо відношення напруження-напруга лінійне, деформація, що виникає внаслідок напруги\(a\sigma\), де\(a\) є постійною, є лише постійною\(a\) напругою, що виникає в результаті\(\sigma\) поодинці. Математично,
\(\epsilon (a \sigma) = a\epsilon (\sigma)\)
Це всього лише випадок «подвоїти стрес, подвоїти напругу».
Якщо деформації повзучості, вироблені в даний час, побудовані як абсциса проти застосованого напруження як ордината, буде вироблена «ізохронна» крива напруження-деформації. Якщо матеріал лінійний, ця «крива» буде прямою лінією, з нахилом, який збільшується в міру зменшення обраного часу.
Для лінійних матеріалів сімейство історій деформацій,\(\epsilon (t)\) отриманих при різних постійних напруженнях, може бути накладено шляхом їх нормалізації на основі прикладеного напруження. Ставлення деформації до напруги називається «комплаєнс»\(C\), а в разі змінного за часом деформації, що виникає внаслідок постійного напруження, відношення є «відповідністю повзучості»:
\(C_{crp} (t) = \dfrac{\epsilon (t)}{\sigma_0}\)
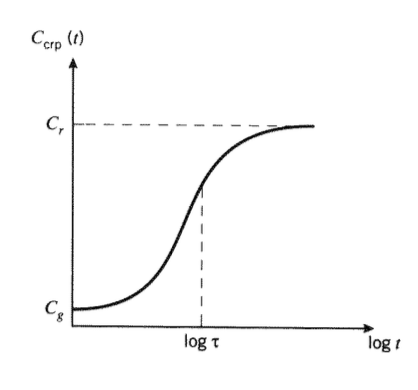
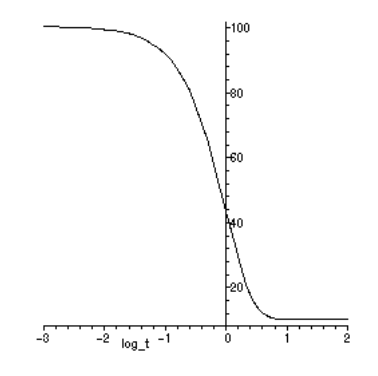
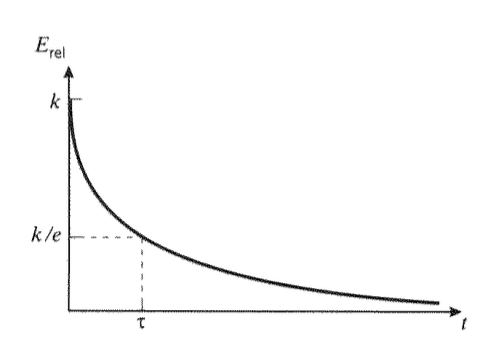
Типова форма цієї функції показана на малюнку 4, побудованому проти логарифма часу. Зверніть увагу, що логарифмічна форма графіка різко змінює форму кривої, розтягуючи короткочасну частину відгуку і стискаючи довготривалу область. При навантаженні матеріал спочатку напружується до «склоподібної» відповідності\(C_g\); це пружна деформація, що відповідає спотворенню зв'язку. Згодом відповідність підвищується до рівноважного або «гумового» значення\(C_r\), відповідного гумовому подовженню матеріалу. Значення вздовж абсцис з позначкою\(\log \tau\) "" позначає перегин від підйому до падіння нахилу і\(\tau\) називається «часом розслаблення» процесу повзучості.
Релаксація стресу
Інший поширений тест, який легко проводиться на Instron або інших машинам, керованих переміщенням, полягає у моніторингу залежного від часу напруження, що виникає внаслідок стійкої деформації, як показано на малюнку 5. Це зворотна цифра 3; тут криві напружень відповідають трьом різним рівням постійної деформації, кожен з яких вдвічі перевищує величину попереднього.
Аналогічно з відповідністю повзучості можна накладати криві релаксації за допомогою «модуля релаксації», визначеного як\(E_{rel}(t) = \sigma (t)/\epsilon_0\), нанесеного на час журналу на малюнку 6. У короткий час напруга знаходиться на високому плато, відповідному «склоподібному» модулю\(E_g\), а потім експоненціально падає до нижчого рівноваги «гумового» модуля,\(E_r\) оскільки молекули полімеру поступово пристосовують деформацію шляхом конформаційного розширення, а не спотворення зв'язку.
Повзучість і розслаблення - це обидва прояви одних і тих же молекулярних механізмів, і слід очікувати, що\(E_{rel}\) і\(C_{crp}\) пов'язані між собою. Втім, хоч\(E_g = 1/C_g\) і\(E_r = 1/C_r\), в цілому\(E_{rel} (t) \ne 1/C_{crp} (t)\). Зокрема, реакція на релаксацію рухається до його рівноваги швидше, ніж реакція повзучості.
Динамічне завантаження
Тести на релаксацію повзучості та стресу зручні для вивчення реакції матеріалу в тривалий час (хвилини до днів), але менш точні в менший час (секунди і менше). Динамічні випробування, в яких вимірюється напруга (або деформація), що виникає внаслідок синусоїдальної деформації (або напруги), часто добре підходять для заповнення «короткочасного» діапазону реакції полімеру. Коли в'язкопружний матеріал піддається синусоїдально змінному напруженню, врешті-решт буде досягнуто стійкий стан (Час, необхідний для того, щоб початковий перехідний ефект згасне, сам буде залежати від в'язкопружного часу відгуку матеріалу, а в деяких ситуаціях це може призвести до експериментальних помилок. Вправа\(\PageIndex{5}\) розвиває повну форму динамічного відгуку, включаючи початковий перехідний термін.), в якій результуюча деформація також синусоїдальна, має ту ж кутову частоту, але затримується у фазі на кут\(\delta\); це аналогічно затриманої деформації, що спостерігається в експериментах з повзучістю. Деформація відстає від напруги за фазовим кутом\(\delta\), і це вірно, навіть якщо деформація, а не напруга, є контрольованою змінною.
Якщо початок по осі часу вибрано так, щоб збігатися з часом, в який деформація проходить через свій максимум, функції деформації і напруги можна записати як:
\[\epsilon = \epsilon_0 \cos \omega t\]
\[\sigma = \sigma_0 \cos (\omega t + \delta\]
Використовуючи алгебраїчний маневр, поширений при аналізі реактивних електричних ланцюгів та інших гармонічних систем, зручно записати функцію напружень як складну величину, реальна частина\(\sigma^*\) якої знаходиться в фазі з деформацією і уявна частина якої з нею\(90^{\circ}\) поза фазою:
\[\sigma^* = \sigma_0' \cos \omega t + i \sigma_0'' \sin \omega t\]
Тут\(i = \sqrt{-1}\) і зірочка позначає складну величину як зазвичай.
Це може бути корисно для візуалізації спостережуваного напруження і деформації як проекції на дійсну вісь векторів, що обертаються в комплексній площині з частотою\(\omega\). Якщо ми захопимо їх положення так само, як вектор деформації проходить реальну вісь, вектор напруги буде випередити його на фазовий кут,\(\delta\) як показано на малюнку 7.
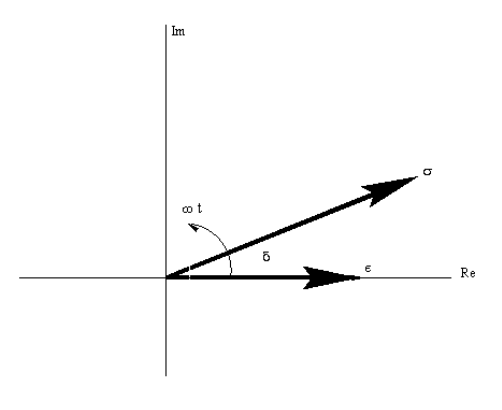
Малюнок 7 дозволяє легко розвивати відносини між різними параметрами в гармонійних відносинях:
\[\tan \delta = \sigma_0''/\sigma_0'\]
\[|\sigma^*| = \sigma_0 = \sqrt{(\sigma_0')^2 + (\sigma_0'')^2}\]
\[\sigma_0' = \sigma_0 \cos \delta\]
\[\sigma_0'' = \sigma_0 \sin \delta\]
Ми можемо використовувати цю складну форму функції напружень для визначення двох різних динамічних модулів, обидва є співвідношеннями напруги до деформації, як зазвичай, але мають дуже різні молекулярні інтерпретації та макроскопічні наслідки. Перший з них - «реальний», або «накопичувальний» модуль, що визначається як відношення напруженості в фазі до деформації:
\[E' = \sigma_0' /\epsilon_0\]
Інший - «уявний», або «втрата», модуль, що визначається як відношення позафазового напруження до деформації:
\[E'' = \sigma_0''/\epsilon_0\]
Приклад\(\PageIndex{1}\)
Терміни «зберігання» і «втрата» можна зрозуміти більш легко, розглядаючи механічну роботу, виконану за цикл завантаження. Величина і\(\int \sigma \ d\epsilon\) є енергією деформації на одиницю об'єму (так як\ сигма\) = сила/площа і\(\epsilon\) = відстань/довжина). Інтеграція інфазових і позафазових компонентів окремо:
\[W = \oint \sigma d \epsilon = \oint \dfrac{d\epsilon}{dt}dt\]
\[=\int_{0}^{2\pi/\omega} (\sigma_0' \cos \omega t)(-\epsilon_0 \omega \sin \omega t) dt + \int_{0}^{2\pi /\omega} (\sigma_0'' \sin \omega t) (-\epsilon_0 \omega \sin \omega t) dt\]
\[= 0 - \pi \sigma_0'' \epsilon_0\]
Зверніть увагу, що внутрішньофазні компоненти не виробляють чистої роботи при інтеграції протягом циклу, тоді як позафазові компоненти призводять до чистого розсіювання за цикл, рівний:
\[W_{dis} = \pi \sigma_0'' \epsilon_0 = \pi \sigma_0 \epsilon_0 \sin \delta\]
Це слід інтерпретувати, щоб проілюструвати, що енергія деформації, пов'язана з фазовим напруженням і деформацією, є оборотною; тобто та енергія, яка зберігається в матеріалі під час циклу завантаження, може бути відновлена без втрат під час розвантаження. І навпаки, енергія, що подається до матеріалу позафазовими компонентами, перетворюється необоротно в тепло.
Максимальна енергія, що зберігається внутрішньофазними компонентами, відбувається в точці чверті циклу, і ця максимальна накопичена енергія становить:
\[\begin{array} {rcl} {W_{st}} & = & {\int_{0}^{\pi /2\omega} (\sigma_0' \cos \omega t)(-\epsilon_0 \omega \sin \omega t) dt} \\ {} & = & {-\dfrac{1}{2} \sigma_0' \epsilon_0 = -\dfrac{1}{2} \sigma_0 \epsilon_0 \cos \delta} \end{array}\]
Відносне розсіювання - відношення\(W_{dis}/W_{st}\) - потім пов'язане з фазовим кутом:
\[\dfrac{W_{dis}}{W_{st}} = 2\pi \tan \delta\]
Нам також буде зручно виражати функції гармонічного напруження та деформації як експоненціальні:
\[\sigma = \sigma_0^* e^{i \omega t}\]
\[\epsilon = \epsilon_0^* e^{i \omega t}\]
\(e^{i \omega t}\)Фактор випливає з відношення Ейлера\(e^{i\theta} = \cos \theta + i \sin \theta\), і запис як напруження, так і деформації як комплексних чисел знімає обмеження розміщення походження в момент максимального деформації, як це було зроблено вище. Складний модуль тепер можна записати просто так:
\[E^* = \sigma_0^* /\epsilon_0^*\]
4. Математичні моделі лінійного в'язкопружного відгуку
4.1 Модель весна-дашпот Максвелла
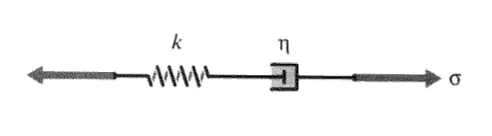
Часова залежність в'язкопружного відгуку аналогічна часовій залежності реактивних електричних кіл, і обидві можуть бути описані однаковими звичайними диференціальними рівняннями в часі. Зручний спосіб розвитку цих відносин, допомагаючи візуалізувати молекулярні рухи, використовує моделі «весна-дашпот». Ці механічні аналоги використовують «Хукеанські» пружини, зображені на малюнку 8 і описані
\(\sigma = k\epsilon\)
де\(\sigma\) і\(\epsilon\) є аналогом сили пружини і зміщення, а постійна пружини\(k\) аналогічна модулю Юнга\(E\);\(k\) тому має одиниці\(N/m^2\). Пружина моделює миттєву деформацію зв'язку матеріалу, і її величина буде пов'язана з часткою механічної енергії, що зберігається оборотно як енергія деформації.

Процес ентропного розмотування є рідкоподібним у природі і може бути змодельований «ньютонівським приладом», також показаним на малюнку 8, в якому напруга виробляє не деформацію, а швидкість деформації:
\(\sigma = \eta \dot{\epsilon}\)
Тут overdot позначає тимчасову диференціацію і η - в'язкість з одиницями\(N-s/m^2\). У багатьох відношеннях, які слід дотримуватися, буде зручно використовувати відношення в'язкості до жорсткості:
\(\tau = \dfrac{\eta}{k}\)
Одиницею\(\tau\) є час, і буде видно, що це співвідношення є корисною мірою часу відгуку в'язкопружного відгуку матеріалу.
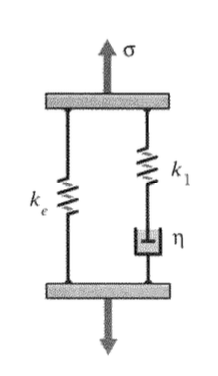
Тверде тіло «Максвелла», показане на малюнку 9, є механічною моделлю, в якій пружина Хукіна і ньютонівський дашпот з'єднані послідовно. Пружина повинна бути візуалізована як представляє пружний або енергетичний компонент відповіді, тоді як дашпот являє собою конформаційний або ентропний компонент. У послідовному з'єднанні, такому як модель Максвелла, напруга на кожному елементі однакова і дорівнює накладеному напруженню, тоді як загальна деформація - це сума деформації в кожному елементі:
\(\sigma = \sigma_s = \sigma_d\)
\(\epsilon = \epsilon_s + \epsilon_d\)
Тут індекси\(s\) і\(d\) представляють пружину і дашпот відповідно. Шукаючи єдине рівняння, що стосується напруження з деформацією, зручно диференціювати рівняння деформації, а потім записати швидкості деформації пружини та дашпота через напругу:
\(\dot{\epsilon} = \dot{\epsilon_s} + \dot{\epsilon_d} = \dfrac{\dot{sigma}}{k} + \dfrac{\sigma}{\eta}\)
Множення\(k\) та використання\(\tau = \eta /k\):
\[k \dot{\epsilon} = \dot{\sigma} + \dfrac{1}{\tau} \sigma\]
Цей вираз є «конститутивним» рівнянням для нашого фіктивного матеріалу Максвелла, рівняння, яке пов'язує напругу з деформацією. Зверніть увагу, що він містить похідні часу, так що простий константи пропорційності між напругою і деформацією не існує. Поняття «модуль» - відношення напруги до деформації - має бути розширено, щоб врахувати цю більш складну поведінку.
Рівняння 5.4.22 може бути вирішене для напруги,\(\sigma (t)\) як тільки\(\epsilon (t)\) деформація вказана, або для деформації, якщо напруга вказана. Два приклади проілюструють цей процес:
Приклад\(\PageIndex{2}\)
У тесті на релаксацію напруження постійна деформація\(\epsilon_0\) діє як «вхід» до матеріалу, і ми шукаємо вираз для результуючого напруження, залежного від часу; це зображено на малюнку 10.
Оскільки в релаксації\(\dot{\epsilon} = 0\) напружень рівняння 5.4.22 стає
\(\dfrac{d \sigma}{dt} = -\dfrac{1}{\tau} \sigma\)
Розділення змінних та інтеграція:
Тут очевидне значення\(\tau \equiv \eta /k\) як характерного «часу релаксації»; це фізично час, необхідний для того, щоб стрес впав до\(1/e\) його початкового значення. Це також час, коли функція напруги проходить через перегин при нанесенні на графік часу журналу.
Модуль релаксації\(E_{rel}\) можна отримати безпосередньо з цього співвідношення, зазначивши, що спочатку лише пружина буде деформуватися, а початкове напруження та деформація пов'язані між собою\(\sigma_0 = k \epsilon_0\). Так
\(E_{rel} (t) = \dfrac{\sigma(t)}{\epsilon_0} = \dfrac{\sigma_0}{\epsilon_0} \exp (-t/\tau)\)
\[E_{rel} (t) = k \exp (-t/\tau)\]
Ця важлива функція побудована схематично на малюнку 11. Два регульовані параметри в моделі,\(k\) і\(\tau\), можуть бути використані, щоб змусити модель відповідати експериментальному графіку модуля релаксації в двох точках. Жорсткість пружини\(k\) буде встановлена на початковий або скляний модуль\(E_g\), і\(\tau\) буде обрана, щоб змусити значення\(k/e\) відповідати експериментальним даними на\(t = \tau\).
Час релаксації\(\tau\) сильно залежить від температури та інших факторів, що впливають на рухливість матеріалу, і приблизно обертається швидкості молекулярного руху. Вгорі\(T_g\),\(\tau\) дуже коротка; внизу\(T_g\) вона дуже довга. Більш детальний розгляд температурної залежності буде дано в більш пізньому розділі, в розрізі «термореологічно простих» матеріалів.
Приклад\(\PageIndex{3}\)
У випадку динамічної реакції залежність часу як напруги, так і деформації мають форму\(\exp (i \omega t)\). Тому всі похідні часу міститимуть вираз\((i \omega) \exp (i \omega t)\), тому Equation 5.4.22 дає:
\(k (i \omega) \epsilon_0^* \exp (i \omega t) = (i \omega + \dfrac{1}{\tau_j}) \sigma_0^* \exp (i \omega t)\)
\(E^*\)Складний модуль тоді
\[E^* = \dfrac{\sigma_0^*}{\epsilon_0^*} = \dfrac{k(i\omega)}{i \omega + \tfrac{1}{\tau_j}} = \dfrac{k(i\omega \tau)}{1 + i \omega \tau}\]
Цим рівнянням можна маніпулювати алгебраїчно (помножити і ділити на комплексний сполучений знаменник), щоб отримати:
\[E^* = \dfrac{k\omega^2 \tau^2}{1 + \omega^2 \tau^2} + i \dfrac{k \omega \tau}{1 + \omega^2 \tau^2}\]
У еквалайзері 5.4.25 дійсна і уявна складові комплексного модуля наведені явно; це відносини «Дебая», також важливі в теорії схем.
4.2 Стандартне лінійне тверде тіло (форма Максвелла)
Більшість полімерів не демонструють необмеженого потоку, дозволеного моделлю Максвелла, хоча це може бути розумною моделлю для Silly Putty або теплої смоли. Тому рівняння 5.4.23 діє лише для дуже обмеженого набору матеріалів. Для більш типових полімерів, конформаційні зміни яких з часом обмежені мережею заплутань або іншими типами точок з'єднання, можна ефективно використовувати більш складні моделі пружинно-приставних точок.
Розміщення пружини паралельно з блоком Максвелла дає дуже корисну модель, відому як «Стандартне лінійне тверде тіло» (S.L.S.), показана на малюнку 12. Ця пружина має жорсткість\(k_e\), названу так, тому що вона забезпечує «рівновагу» або гумову жорсткість, яка залишається після того, як напруги в руці Максвелла розслабляються, коли dashpot розширюється.
У такому розташуванні рука Максвелла і паралельна пружина\(k_e\) відчувають однакову напругу, а\(\sigma\) загальне напруження - це сума напруги в кожній руці:\(\sigma = \sigma_e + \sigma_m\). Незручно вирішувати напругу\(\sigma_m\) в плечі Максвелла за допомогою рівняння 5.4.22, оскільки це містить як напругу, так і його похідну за часом. Перетворення Лапласа дуже зручно в цій та інших задачах в'язкопружності, оскільки воно зводить диференціальні рівняння до алгебраїчних. Додатки A перераховує деякі пари перетворень, які часто зустрічаються в цих проблемах.
Оскільки напруга і деформація дорівнюють нулю, коли початок наближається зліва, перетворення похідних часу - це просто змінна Лапласа s разів перетворення функцій; позначаючи перетворені функції з оверлінією, ми маємо\(\mathcal{L} (\dot{\epsilon}) = s \bar{\epsilon}\) і\(\mathcal{L} (\dot{\sigma}) = s \bar{\sigma}\). Потім запис перетворення виразу, такого як Equation 5.4.22, виконується простим розміщенням рядка над залежними від часу функціями та заміною похідної за часом overdot на коефіцієнт s:
\(k \dot{\epsilon} = \dot{\sigma_m} + \dfrac{1}{\tau} \sigma_m \to k_1 s \bar{\epsilon} = s \bar{\sigma_m} + \dfrac{1}{\tau} \bar{\sigma_m}\)
Рішення для\(\bar{\sigma_{m}}\):
\[\bar{\sigma_m} = \dfrac{k_1 s}{s + \tfrac{1}{\tau}} \bar{\epsilon}\]
Додаючи напругу\(\bar{\sigma_e} = k_e \bar{\epsilon}\) в пружині рівноваги, загальне напруження становить:
\(\bar{\sigma} = k_e \bar{\epsilon} + \dfrac{k_1 s}{s + \tfrac{1}{\tau}} \bar{\epsilon} = \left \{ k_e + \dfrac{k_1 s}{s + \tfrac{1}{\tau}} \right \} \bar{\epsilon}\)
Цей результат можна записати
\[\bar{\sigma} = \mathcal{E} \bar{\epsilon}\]
де для цієї моделі\(\mathcal{E}\) параметр
\[\mathcal{E} = k_e + \dfrac{k_1 s}{s + \tfrac{1}{\tau}}\]
Рівняння 5.4.27, яке явно нагадує Закон Гука,\(\sigma = E_{\epsilon}\) але в площині Лапласа, називається пов'язаним в'язкопружним складовим рівнянням. Тут конкретний вираз для\(\mathcal{E}\) моделі Standard Linear Solid, але інші моделі могли бути використані і інші моделі.
Для заданої вхідної функції\(\epsilon (t)\) деформації отримаємо результуючу функцію напружень у три етапи:
1. Отримати вираз для перетворення функції деформації,\(\bar{\epsilon} (s)\).
2. Сформувати алгебраїчний твір\(\bar{\sigma} (s) = \mathcal{E} \bar{\epsilon} (s)\).
3. Отримати обернене перетворення результату для отримання функції напружень у часовій площині.
Приклад\(\PageIndex{4}\)
У разі розслаблення напруги функція деформації\(\epsilon (t)\) розглядається як постійний\(\epsilon_0\) час функції «Хевісайд» або «одиничний крок»\(u(t)\):
\(\epsilon (t) = \epsilon_0 u(t), \ \ \ \ u(t) = \begin{cases} 0, & t < 0\\ 1, & t \ge 0\end{cases}\)
Це має перетворення Лапласа
\(\bar{\epsilon} = \dfrac{\epsilon_0}{s}\)
Використовуючи це в рівнянні 5.4.27 і діливши через на\(\epsilon_0\), ми маємо
\(\dfrac{\bar{\sigma}}{\epsilon_0} = \dfrac{k_e}{s} + \dfrac{k_1}{s + \tfrac{1}{\tau}}\)
Так як\(\mathcal{L}^{-1} 1/(s + a) = e^{-at}\), це може бути перевернуто безпосередньо, щоб дати
\[\dfrac{\sigma (t)}{\epsilon_0} \equiv E_{rel} (t) = k_e + k_1 \exp (-t/\tau)\]
Ця функція, яка є лише моделлю Максвелла, зміщеною вгору на величину\(k_e\), використовувалася для генерації кривої, показаної на малюнку 6.
Приклад\(\PageIndex{5}\)
Форма Рівняння 5.4.27 зручна, коли бажане напруження, необхідне для створення заданої деформації. Дещо незручно, коли бажана деформація, породжена заданою напругою, так як тоді параметр\(\mathcal{E}\) з'являється в знаменнику:
\(\bar{\epsilon} = \dfrac{\bar{\sigma}}{\mathcal{E}} = \dfrac{\bar{\sigma}}{k_e + \dfrac{k_1 s}{s + \tfrac{1}{\tau}}}\)
Це складніше інвертувати, і в таких випадках\(^{\text{TM}}\) може бути корисним програмне забезпечення для символічних маніпуляцій, наприклад Maple. Наприклад, якщо ми хочемо обчислити відповідність повзучості стандартного лінійного твердого тіла Максвелла, ми могли б написати:
read transformation library
> with(inttrans):
define governing equation
> eq1:=sigbar=EE*epsbar;
Constant stress sig0:
> sigbar:=laplace(sig0,t,s);
EE viscoelastic operator - Maxwell S.L.S. model
> EE:= k[e]+k[1]*s/(s+1/tau);
Solve governing equation for epsbar and invert:
> C[crp](t):=simplify((invlaplace(solve(eq1,epsbar),s,t))/sig0);
k[e] t
-k[e] - k[1] + k[1] exp(- -------------------)
tau (k[e] + k[1])
C[crp](t) := - -----------------------------------------------
k[e] (k[e] + k[1])
Цей результат можна записати як
\[C_{crp} (t) = C_g + (C_r - C_g) (1 - e^{-t/\tau_c})\]
де
\(C_g = \dfrac{1}{k_e + k_1}, \ \ C_r = \dfrac{1}{k_e}, \ \ \tau_c = \tau (\dfrac{k_e + k_1}{k_e})\)
Склоподібна відповідність\(C_g\) - це відповідність двох пружин\(k_e\) і\(k_1\) діють паралельно, а відповідність гумі\(C_r\) - це\(k_e\) лише пружина, як і очікувалося. Менш очевидним є те, що характерний час для повзучості\(\tau_c\) (іноді його називають часом «затримки») більше\(\tau\), ніж характерний час для розслаблення, в рази рівний відношенню склоподібного до гумового модуля. Це загальний результат, не обмежуючись конкретною використовуваною моделлю.
Менш незручна форма для проблем з відповідністю створюється, коли використовуються моделі типу «Voigt», а не Maxwell-типу; див. Вправи\(\PageIndex{7}\) та вправи\(\PageIndex{8}\).
Standard Linear Solid - це трипараметрична модель, здатна описувати\(k_1\) загальні риси в'язкопружної релаксації:\(k_e\) і обрані відповідно до скляних і гумових модулів, і\(\tau\) вибирається для розміщення релаксації в правильний часовий проміжок:
\[k_e = E_r\]
\[k_1 = E_g - E_r\]
\[\tau = t @ E_{rel} = (E_r + \dfrac{1}{e} (E_g - E_r))\]
Це змушує прогноз S.L.S. відповідати експериментальним даними у трьох точках, але здатність моделі відповідати експериментальним даними у повному діапазоні релаксації, як правило, бідна. Модуль релаксації, передбачений S.L.S. падає від\(E_g\) до приблизно\(E_r\) за два десятиліття («десятиліття» часу в нашому контексті кратне десяти, скажімо, від 103 до 104 секунд, а не проміжок десяти років.) часу, що, як правило, занадто різкий перехід.
4.3 Модель Віхерта
Справжній полімер не розслабляється жодним часом релаксації, як передбачали попередні моделі. Молекулярні сегменти різної довжини сприяють розслабленню, причому більш прості і короткі сегменти розслабляються набагато швидше, ніж довгі. Це призводить до розподілу часу релаксації, що, в свою чергу, виробляє розслаблення, що поширюється протягом набагато більш тривалого часу, ніж може бути змодельовано точно за допомогою одного часу релаксації. Коли інженер вважає за необхідне включити цей ефект, модель Віхерта, проілюстрована на малюнку 13, може мати стільки пружинних елементів Максвелла, скільки потрібно для задовільного наближення розподілу.
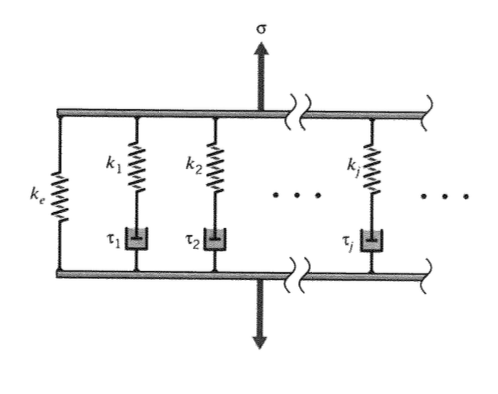
Сумарне напруження,\(\sigma\) що передається моделлю, - це напруга в ізольованій пружині (жорсткості\(k_e\)) плюс, що в кожному з пружинних важелів Максвелла:
\(\sigma = \sigma_e + \sum_j \sigma_j\)
З рівняння 5.4.26 напруга в плечі Максвелла дорівнює
\(\overline{\sigma_j} = \dfrac{k_j s \bar{\epsilon}}{(s + \tfrac{1}{\tau_j})}\)
Тоді
\[\bar{\sigma} = \bar{\sigma}_e + \sum_j \bar{\sigma}_j = \left \{ k_e + \sum_j \dfrac{k_j s}{(s + \tfrac{1}{\tau_j})} \right \} \bar{\epsilon}\]
Величина в дужках - це оператор модуля в'язкопружності,\(\mathcal{E}\) визначеного в Рівнянні 5.4.27 для моделі Віхерта.
Приклад\(\PageIndex{6}\)
У тестах на релаксацію стресу ми маємо
\(\epsilon (t) = \epsilon_0 \Rightarrow \bar{\epsilon} (s) = \epsilon_0/s\)
\(\bar{\sigma} (s) = \mathcal{E} (s) \bar{\epsilon} (s) = \left \{ k_e + \sum_j \dfrac{k_j s}{s + \tfrac{1}{\tau_j}} \right\} \dfrac{\epsilon_0}{s} = \left \{ \dfrac{k_e}{s} + \sum_j \dfrac{k_j}{s + \tfrac{1}{\tau_j}}\right\} \epsilon_0\)
\[\sigma (t) = \mathcal{L}^{-1} [\bar{\sigma} (s)] = \left \{k_e + \sum_j k_j \exp (\dfrac{-t}{\tau_j}) \right \} \epsilon_0\]
Розділивши на\(\epsilon_0\), модуль релаксації дорівнює
\[E_{rel} (t) = k_e + \sum_j k_j \exp (\dfrac{-t}{\tau_j})\]
Матеріальні константи в цьому виразі (\(k_e\)і різні\(k_j\) і\(\tau_j\)) можуть бути обрані шляхом примусу прогнозованих значень Ереля (t), заданих рівнянням 5.4.36, відповідати тим, що визначені експериментально. Вправа\(\PageIndex{19}\) дає приклад такої процедури.
Приклад\(\PageIndex{7}\)
Розглянемо функцію напруги, отриману в результаті тесту з постійною швидкістю деформації:
\(\epsilon = R_{\epsilon} t \to \bar{\epsilon} (s) = R_{\epsilon}/s^2\)
де\(R_{\epsilon}\) - швидкість деформації. Тоді
\(\bar{\sigma} = \mathcal{E} (s) \bar{\epsilon} (s) = \left [k_e + \sum_j \dfrac{k_j s}{s + \tfrac{1}{\tau_j}} \right ] \dfrac{R_{\epsilon}}{s^2} = \dfrac{k_e R_{\epsilon}}{s^2} + \sum_j \dfrac{k_j R_{\epsilon}}{s(s + \tfrac{1}{\tau_j})}\)
\[\sigma (t) = k_e R_{\epsilon} t + \sum_j k_j R_{\epsilon} \tau_j [1 - \exp (-t/\tau_j)]\]
Зверніть увагу, що функція напруження-час, а отже, і крива напруження-деформація, не є лінійною. Тому неправда, що криволінійна діаграма напруження-деформація означає, що реакція матеріалу нелінійна. Цікаво також відзначити, що нахил кривої напруження-деформації з постійною швидкістю деформації пов'язаний зі значенням модуля релаксації, оцінюваного одночасно:
\(\dfrac{d \sigma}{d \epsilon} = \dfrac{d\sigma}{dt} \cdot \dfrac{dt}{d\epsilon} = \dfrac{d\sigma}{dt} \cdot \dfrac{1}{R_{\epsilon}} = \left [k_e R_{\epsilon} + \sum_j k_j R_{\epsilon} \exp (-t/\tau_j) \right ] \dfrac{1}{R_{\epsilon}}\)
\[= \left [ k_e + \sum_j k_j \exp (-t/\tau_j) \right ] \equiv E_{rel} (t) |_{t = \epsilon/R_{\epsilon}}\]
Приклад\(\PageIndex{8}\)
Може бути, що вхідна функція деформації не відома як математичний вираз, або її математичний вираз може бути настільки складним, що робить процес перетворення нерозв'язним. У цих випадках можна повернутися до диференціального складового рівняння та переробити його у скінченно-різницевій формі, щоб отримати числове рішення. Нагадаємо, що\(j\) напруга в руці моделі Віхерта дається
\[\dfrac{d \sigma_j}{dt} + \dfrac{1}{\tau_j} \sigma_j = k_j \dfrac{d\epsilon}{dt}\]
Це може бути записано у формі скінченної різниці як
\[\dfrac{\sigma_j^t - \sigma_j^{t - 1}}{\Delta t} + \dfrac{1}{\tau_j} \sigma_j^t = k_j \dfrac{\epsilon^t - \epsilon^{t - 1}}{\Delta t}\]
де\(t\) надписи і\(t - l\) вказують значення до і після проходження невеликого часового приросту\(\Delta t\). Рішення для\(\sigma_j^t\):
\[\sigma_j^t = \dfrac{1}{1 + (\Delta t/\tau_j)} [k_j (\epsilon^t - \epsilon^{t - 1}) + \sigma_j^{t - 1}]\]
Тепер підсумовуємо всі плечі моделі і додаємо напругу в пружину рівноваги:
\[\sigma^t = k_e \epsilon^t + \sum_j \dfrac{k_j (\epsilon^t - \epsilon^{t - 1}) + \sigma_j^{t - 1}}{1 + (\Delta t/\tau_j)}\]
Це являє собою рекурсивний алгоритм, який комп'ютер може використовувати для обчислення послідовних значень\(\sigma^t\) початку в\(t = 0\). На додаток до зберігання різних\(k_j\) і\(\tau_j\) які складають опис матеріалу, комп'ютер також повинен зберігати попередні значення кожного напруги руки (The\(\sigma_j^{t-1}\)) в зберіганні.
4.4 Суперпозиція Больцмена Інтегральна
Як видно з попередніх розділів, лінійна в'язкопружність може бути заявлена в терміні механічних моделей, побудованих з лінійних пружин і приставних точок. Ці моделі генерують конститутивні відносини, які є звичайними диференціальними рівняннями; див. Вправи\(\PageIndex{13}\) та вправи\(\PageIndex{14}\) як приклади цього. Однак можуть бути використані інтегральні рівняння, і цей інтегральний підхід також використовується як відправна точка для в'язкопружної теорії.
Інтеграли - це операції підсумовування, і цей погляд на в'язкопружність приймає відповідь матеріалу в момент t як сума відповідей на збудження, накладені у всі попередні часи. Здатність підсумувати ці індивідуальні відповіді вимагає від матеріалу підкорятися більш загальному твердженню лінійності, ніж ми посилалися раніше, зокрема, що реакція на ряд індивідуальних збуджень є сумою відповідей, які були б породжені кожним збудженням, що діє окремо. Математично, якщо напруга внаслідок деформації\(\epsilon_1 (t)\) є\(\sigma (\epsilon_1)\) і що через різну деформацію\(\epsilon_2 (t)\) є\(\sigma (\epsilon_2)\), то напруга, обумовлена обома деформаціями, є\(\sigma (\epsilon_1 + \epsilon_2) = \sigma (\epsilon_1) + \sigma (\epsilon_2)\). Поєднуючи це з умовою мультиплікативного масштабування, використаного раніше, ми маємо як загальне твердження лінійної в'язкопружності:
\[\sigma (a \epsilon_1 + b \epsilon_2) = a \sigma (\epsilon_1) + b\sigma (\epsilon_2)\]
З цього визначення випливає з цього визначення «Інтеграл суперпозиції Больцмана» твердження лінійної в'язкопружної відповіді. Розглянемо напругу\(\sigma_1 (t)\) в часі\(t\) через застосування невеликої деформації,\(\Delta_{\epsilon_1}\) застосованої в той час, що\(\xi_1\) попередній\(t\); це дається безпосередньо з визначення модуля релаксації як
Аналогічно, напруга\(\sigma_2 (t)\) внаслідок збільшення деформації,\(\Delta_{\epsilon_2}\) застосованого в інший час\(\xi_2\), є
Якщо матеріал лінійний, сумарне напруження в часі\(t\) через обидва приросту деформації разом може бути отримано шляхом накладання цих двох окремих ефектів:
Оскільки кількість застосованих приростів деформації збільшується, щоб наблизитися до безперервного розподілу, це стає:
\[\to \sigma(t) = \int_{-\infty}^{t} E_{rel} (t - \xi)d\epsilon =\int_{-\infty}^{t} E_{rel} (t - \xi) \dfrac{d\epsilon (\mathcal{E})}{d\mathcal{E}} d\mathcal{E}\]
Приклад\(\PageIndex{9}\)
У разі постійної швидкості деформації\((\epsilon (t) = R_{\epsilon} t)\) ми маємо
\(\dfrac{d\epsilon (\xi)}{d\xi} = \dfrac{d(R_{\epsilon} \xi)}{d\xi} = R_{\epsilon}\)
Для відповіді на матеріали S.L.S.\((E_{rel} (t) = k_e + k_1 \exp [-t/\tau])\),
Рівняння 5.4.44 дає напругу як
Maple заяви для проведення цих операцій можуть бути:
define relaxation modulus for S.L.S. >Erel:=k[e]+k[1]*exp(-t/tau); define strain rate >eps:=R*t; integrand for Boltzman integral >integrand:=subs(t=t-xi,Erel)*diff(subs(t=xi,eps),xi); carry out integration >’sigma(t)’=int(integrand,xi=0..t);
що дає результат:
Це ідентично рівнянню 5.4.37, з однією рукою в моделі.
Інтегральне відношення Больцмана можна отримати формально, нагадавши, що перетворений модуль релаксації пов'язаний просто з пов'язаним модулем в'язкопружності в площині Лапласа як
стресове розслаблення:\(\epsilon (t) = \epsilon_0 u(t) \to \bar{\epsilon = \dfrac{\epsilon_0}{s}\)
\(\bar{\sigma} = \mathcal{E} \bar{\epsilon} = \mathcal{E} \dfrac{\epsilon_0}{s}\)
\(\dfrac{\bar{\sigma}}{\epsilon_0} = \bar{E}_{rel} (s) = \dfrac{1}{s} \mathcal{E} (s)\)
Так як\(s\bar{f} = \bar{\dot{f}}\), дотримуються такі відносини:
\(\bar{\sigma} = \mathcal{E} \bar{\epsilon} = s \bar{E}_{rel} \bar{\epsilon} = \bar{\dot{E}}_{rel} \bar{\epsilon} = \bar{E}_{rel} \bar{\dot{\epsilon}}\)
Останні два з перерахованих вище мають вигляд, для якого застосовується інтегральне перетворення згортки (див. Додаток А), тому наступні чотири еквівалентні співвідношення виходять відразу:
\[\begin{array} {rcl} {\sigma (t)} & = & {\int_0^t E_{rel} (t - \xi) \dot{\epsilon} (\xi) d \xi} \\ {} & = & {\int_0^t E_{rel} (\xi) \dot{\epsilon} (t - \xi) d \xi} \\ {} & = & {\int_0^t \dot{E}_{rel} (t - \xi) \epsilon (\xi) d \xi} \\ {} & = & {\int_0^t \dot{E}_{rel} (\xi) \epsilon (t - \xi) d \xi} \end{array}\]
Ці відносини є формами формули Дюамеля, де\(E_{rel}(t)\) можна інтерпретувати як напруга,\(\sigma (t)\) що виникає в результаті одиниці введення деформації. Якщо напруга, а не деформація є вхідною величиною, то аналогічний розвиток призводить до
\[\epsilon (t) = \int_0^t C_{crp} (t - \xi) \dot{sigma} (\xi) d \xi\]
де\(C_{crp} (t)\) реакція деформації на вхідні одиниці напруги - величина, визначена раніше як відповідність повзучості. Співвідношення між відповідністю повзучості та модулем релаксації тепер можна розробити як:
\(\bar{\sigma} = s \bar{E}_{rel} \bar{\epsilon}\)
\(\bar{\epsilon} = s \bar{C}_{crp} \bar{\sigma}\)
\(\bar{\sigma} \bar{\epsilon} = s^2 \bar{E}_{rel} \bar{C}_{crp} \bar{\epsilon} \bar{\sigma} \to \bar{E}_{rel} \bar{C}_{crp} = \dfrac{1}{s^2}\)
Видно, що потрібно вирішити інтегральне рівняння, щоб отримати функцію повзучості з функції релаксації, або навпаки. Цей процес деконволюції іноді може виконуватися аналітично (ймовірно, з використанням трансформацій Лапласа), і в труднорозв'язних випадках було використано деяке використання nu-merical підходів.
4.5 Вплив температури
Як уже згадувалося на самому початку (\(cf\). Рівняння 5.4.2) температура має різкий вплив на показники віс-копружного відгуку, і в практичній роботі часто доводиться коригувати в'язкопружний аналіз для різної температури. Ця сильна залежність температури також може бути корисною в експериментальній характеристиці: якщо, наприклад, в'язкопружний перехід відбувається занадто швидко при кімнатній температурі для легкого вимірювання, експериментатор може знизити температуру, щоб уповільнити ситуацію.
У деяких полімерах, особливо «простих» матеріалах, таких як поліізобутилен та інші аморфні термопласти, які мають мало ускладнюючих особливостей у своїй мікроструктурі, співвідношення між часом і температурою можна описати відповідно простими моделями. Такі мате- ріали називаються «термореологічно простими».
Для таких простих матеріалів ефект зниження температури полягає в тому, щоб просто зсунути в'язкопружний відгук (нанесений проти часу журналу) вправо без зміни форми. Це еквівалентно збільшенню часу релаксації\(\tau\), наприклад, в Eqns. 5.4.29 або 5.4.30, без зміни склоподібних або гумових модулів або відповідності. «Коефіцієнт зсуву часової температури»\(a_T (T)\) можна визначити як горизонтальний зсув, який повинен бути застосований до кривої відгуку, скажімо\(C_{crp} (t)\), виміряної при\(T\) довільній температурі, щоб перемістити її до кривої, виміряної при певній еталонній температурі\(T_{ref}\).
\[\log (a_T) = \log \tau (T) - \log \tau (T_{ref})\]
Це зсув схематично показано на малюнку 14.
Малюнок 14: Коефіцієнт зсуву часової температури.
У вищесказаному ми припускаємо один час релаксації. Якщо модель містить кілька разів релаксації, термореологічна простота вимагає, щоб усі мали однаковий коефіцієнт зсуву, оскільки в іншому випадку крива відгуку змінила б форму, а також положення, коли температура змінюється.
Якщо час розслаблення підпорядковується Arrhenius відношення форми\(\tau (T) = \tau_0 \exp (E^{\dagger}/RT)\), коефіцієнт зсуву легко показано як (див. Вправа\(\PageIndex{17}\))
\[\log a_T = \dfrac{E^{\dagger}}{2.303 R} (\dfrac{1}{T} - \dfrac{1}{T_{ref}})\]
Тут коефіцієнтом\(2.303 = \ln 10\) є перетворення між природним і базовим 10 логарифмами, які зазвичай використовуються для полегшення графічного побудови за допомогою журналу паперу.
Хоча кінетична обробка Arrhenius зазвичай застосовується до вторинних полімерних переходів, багато працівників вважають, що первинний перехід скло-гума, здається, регулюється іншими принципами. Популярною альтернативою є використання рівняння «W.L.F.» при температурах поблизу або вище температури скла:
\[\log a_T = \dfrac{-C_1 (T- T_{ref}}{C_2 + (T - T_{ref})}\]
Ось\(C_1\) і\(C_2\) довільні матеріальні константи, значення яких залежать від матеріалу і вибору еталонної температури\(T_{ref}\). Було встановлено, що якщо\(T_{ref}\) вибирається бути\(T_g\), то\(C_1\) і\(C_2\) часто припускають «універсальні» значення, застосовні до широкого спектру полімерів:
\[\log a_T = \dfrac{-17.4 (T - T_g)}{51.6 + (T- T_g)}\]
де\(T\) знаходиться за Цельсієм. Оригінальний W.L.F. папір (М.Л. Вільямс, Р.Ф. Ландель, і J.D Феррі, J.Am. Хім. Soc., Vol. 77, No. 14, pp. 3701—3707, 1955.) розвивав це відношення емпірично, але раціоналізував його з точки зору концепцій вільного обсягу.
Серія даних повзучості або релаксації, прийнятих за діапазон температур, може бути перетворена в одну «головну криву» за допомогою цього горизонтального зсуву. Конкретна крива вибирається як еталонна, потім інші криві зміщуються горизонтально, щоб отримати одну криву, що охоплює широкий діапазон часу журналу, як показано на малюнку 15. Криві, що представляють дані, отримані при температурах, нижчих за еталонну температуру, з'являються в більш тривалий час, праворуч від опорної кривої, тому доведеться зрушити вліво; це позитивний зсув, оскільки ми визначили коефіцієнт зсуву в Рівнянні 5.4.47. Кожна крива виробляє своє власне значення\(a_T\), так що\(a_T\) стає табличною функцією температури. Майстер-крива діє тільки при еталонній температурі, але її можна використовувати і при інших температурах, змістивши її на відповідне значення колоди\(a_T\).
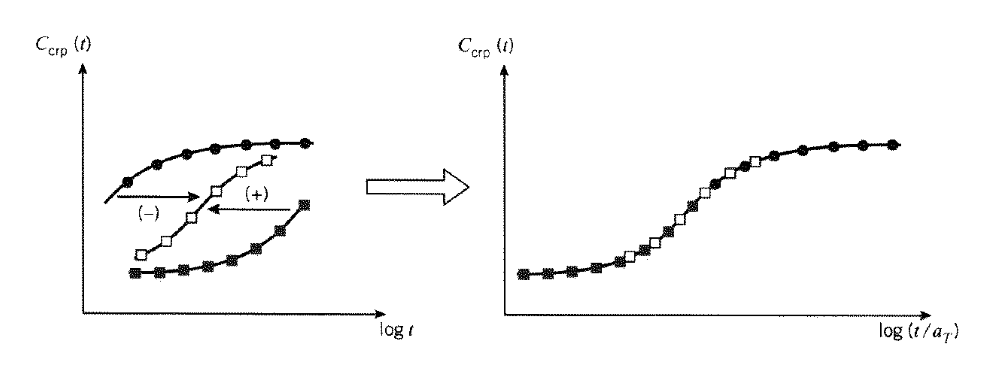
Маркування абсциси, як на\(\log(t/a_T) = \log t - \log a_t\) малюнку 15, заслуговує деякого обговорення. Замість того, щоб зміщувати головну криву вправо для температур, менших за еталонну температуру, або вліво для більш високих температур, простіше просто змінити нумерацію осі, збільшивши цифри для низьких температур і зменшуючи їх для високих. Тому мітка вказує на те, що числові значення на горизонтальній осі були відрегульовані для температури шляхом віднімання журналу коефіцієнта зсуву. Оскільки нижчі температури мають позитивні коефіцієнти зсуву, цифри менші, ніж вони повинні бути, і їх потрібно збільшувати відповідним коефіцієнтом зсуву. Маркування осей таким чином, безперечно, неоднозначне і, як правило, заплутане, але правильне регулювання легко здійснюється, пам'ятаючи, що нижчі температури сповільнюють швидкість повзучості, тому час потрібно робити довше, збільшуючи цифри на осі. І навпаки, для більш високих температур цифри повинні бути зроблені меншими.
Приклад\(\PageIndex{10}\)
Ми хочемо знайти ступінь повзучості в двотемпературному циклі, який складається з\(t_1 = 10\) годин на 20,\(^{\circ}C\) а потім\(t_2 = 5\) хвилин при 50\(^{\circ}C\). Коефіцієнт зсуву колоди для 50\(^{\circ}C\), щодо еталонної температури 20\(^{\circ}C\), як відомо, становить -2,2.
Використовуючи заданий коефіцієнт зсуву, ми можемо відрегулювати час другої температури при 50\(^{\circ}C\) до еквівалентного часу\(t_2'\) в 20\(^{\circ}C\) наступним чином:
\(t_2' = \dfrac{t_2}{a_T} = \dfrac{\text{5 min}}{10^{-2.2}} = 792 \text{ min} = 13.2 \text{ h}\)
Отже, 5 хвилин при 50\(^{\circ}C\) еквівалентно понад 13 годин на 20\(^{\circ}C\). Загальний ефективний час - це сума двох температурних кроків:
\(t' = t_1 + t_2' = 10 + 13.2 = 23.2 \text{ h}\)
Загальна повзучість тепер може бути оцінена за допомогою цього ефективного часу у відповідному співвідношенні для повзучості, наприклад Equation 5.4.30.
Ефективно-часовий підхід до реагування при різних температурах може бути поширений на довільну кількість температурних ступенів:
\(t' = \sum_j t_j' = \sum_j (\dfrac{t_j}{a_T (T_j)})\)
Для залежних від часу температур в цілому ми маємо\(T = T(t)\), тому\(a_T\) стає неявною функцією часу. Ефективний час може бути записаний для безперервних функцій як
\[t' = \int_0^t \dfrac{d\xi}{a_T (\xi)}\]
де\(\xi\) є фіктивна змінна часу. Цей підхід, хоча і здається дещо абстрактним, має значне застосування при моделюванні реакції матеріалів, що залежать від часу. Такі фактори, як пошкодження внаслідок застосованого стресу або впливу навколишнього середовища, можуть прискорити або уповільнити швидкість заданої реакції, і ця зміна швидкості може бути описана коефіцієнтом розширення часу, подібним до АТ, але залежним від інших факторів, крім температури.
Приклад\(\PageIndex{11}\)
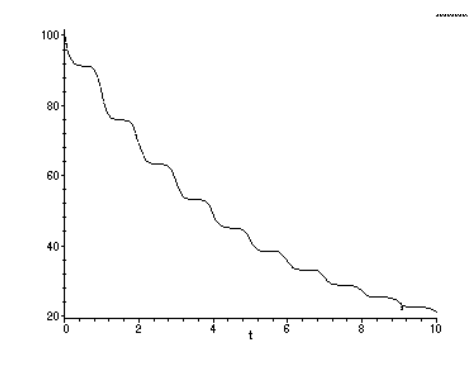
Розглянемо гіпотетичний полімер з часом релаксації, виміряним при 20\(^{\circ}C\) of\(\tau\) = 10 днів, і зі склоподібними і гумовими модулями\(E_g = 100\),\(E_r = 10\). Полімер може бути прийнятий, щоб підкорятися рівнянню W.L.F. з розумною точністю, при\(T_g\) = 0\(^{\circ}C\). Ми хочемо обчислити модуль релаксації у випадку температури, яка змінюється синусоїдально\(\pm\) 5\(^{\circ}\) навколо 20\(^{\circ}C\) протягом дня. Це може бути досягнуто за допомогою ефективного часу, обчисленого з Рівняння 5.4.51 в Рівнянні 5.4.29, як показано в наступних командах Maple:
define WLF form of log shift factor >log_aT:=-17.4*(T-Tg)/(51.6+(T-Tg)); find offset; want shift at 20C to be zero >Digits:=4;Tg:=0;offset:=evalf(subs(T=20,log_aT)); add offset to WLF >log_aT:=log_aT-offset; define temperature function >T:=20+5*cos(2*Pi*t); get shift factor; take antilog >aT:=10^log_aT; replace time with dummy time variable xi >aT:=subs(t=xi,aT); get effective time t’ >t_prime:=int(1/aT,xi=0..t); define relaxation modulus >Erel:=ke+k1*exp(-t_prime/tau); define numerical parameters >ke:=10;k1:=90;tau:=10; plot result >plot(Erel,t=0..10);
5 Аналіз в'язкопружних напружень
5.1 Багатовісні стресові стани
В'язкопружні вирази вище посилалися на простий напружений стан, в якому зразок піддається одновісному натягу. Це навантаження має відношення до лабораторних випробувань характеристик, але інформація, отримана в результаті цих випробувань, повинна бути відлита у формі, яка дозволяє застосовувати до багатовісних напружених станів, які зустрічаються в реальному проектуванні.
Багато формул для напружень і переміщення в задачах будівельної механіки відлиті у формах, що містять модуль Юнга\(E\) і коефіцієнт Пуассона\(ν\). Щоб адаптувати ці відносини для в'язкопружного відгуку, можна спостерігати як поздовжню, так і поперечну реакцію в тесті на розтяг, щоб обидва\(E(t)\) і\(ν(t)\) могли бути визначені. Моделі потім можуть бути пристосовані до обох режимів деформації, щоб знайти відповідні в'язкопружні оператори\(\mathcal{E}\) і\(\mathcal{N}\). Однак часто зручніше використовувати модуль зсуву та об'ємний модуль,\(K\) а не\(G\)\(E\) і\(ν\), що можна зробити, використовуючи співвідношення, дійсні для ізотропних лінійних пружних матеріалів:
\[E= \dfrac{9GK}{3K + G}\]
\[v =\dfrac{3K - 2G}{6K + 2G}\]
Ці важливі відносини випливають з геометричних або рівноважних аргументів і не передбачають міркування реакції, що залежить від часу. Оскільки перетворення Лапласа впливає на часові, а не просторові параметри, відповідні в'язкопружні оператори підкоряються аналогічним відносинам в площині Лапласа:
\(\mathcal{E} (s) = \dfrac{9\mathcal{G}(s) \mathcal{K}(s)}{3\mathcal{K}(s) + \mathcal{G}(s)}\)
Рисунок 17: Модулі релаксації поліізобутилену при розширенні (\(K\)) та зсуві (\(G\)). Від Хуан, М.Г., Лі, Е.Х., і Роджерс, Т.Г., «Про вплив в'язкопружної стисливості в аналізі напружень» Технічний звіт Стенфордського університету № 140 (1963).
Ці заміни корисні тим, що зазвичай\(K(t)\) набагато більше\(G(t)\), ніж, і\(K(t)\) зазвичай відчуває набагато менші розслаблення, ніж\(G(t)\) (див. Рис. 17). Ці спостереження призводять до ідеалізації стисненості, що значно спрощує аналіз. По-перше, якщо взяти кінцевий\(K_{rel} = K_e\), але постійний (тільки реакція на зсув в'язкопружний), то
\(\mathcal{K} = s \bar{K}_{rel} = s \dfrac{K_e}{s} = K_e\)
По-друге, якщо\(K\) передбачається не тільки постійне, але і нескінченне (матеріал нестисливий, немає гідростатичної деформації), то
\(\mathcal{G} = \dfrac{\mathcal{E}}{3}\)
\(\mathcal{N} = v = \dfrac{1}{2}\)
Приклад\(\PageIndex{12}\)
Модуль зсуву полівінілхлориду (ПВХ) спостерігається для розслаблення від склоподібного значення\(G_g = 800\) МПа до гумового значення\(G_r =1.67\) МПа. Час релаксації в 75\(^{\circ} C\) становить приблизно\(\tau =100\) с, хоча перехід набагато ширший, ніж було б передбачено однією моделлю часу релаксації. Але припускаючи стандартну лінійну тверду модель як наближення, оператор зсуву
Об'ємний модуль постійний хорошому наближенню при\(K_e =1.33\) ГПа. Ці дані можуть бути використані для прогнозування часової залежності коефіцієнта Пуассона, використовуючи вираз
При підстановці числових значень і спрощенні це стає
\(\mathcal{N} = 0.25 + \dfrac{9.97 \times 10^8}{4.79 \times 10^{11} s + 3.99 \times 10^9}\)
Коефіцієнт «релаксації» Пуассона - залежна від часу деформація в одному напрямку, індукована постійною деформацією в поперечному напрямку - тоді
\(\bar{v}_{rel} = \dfrac{\mathcal{N}}{s} = \dfrac{0.25}{s} + \dfrac{1}{s} (\dfrac{9.97 \times 10^8}{4.79 \times 10^{11} s + 3.99 \times 10^9})\)
Інвертуючи, це дає
Ця функція побудована на малюнку 18. Схоже, що коефіцієнт Пуассона піднімається від склоподібного значення 0,25 до гумового значення 0,5, оскільки матеріал з часом рухається від склоподібного до гумового режиму. Зверніть увагу, що постійна часу 120 с у вищевказаному виразі не збігається з часом релаксації\(\tau\) для чистої реакції на зсув.
Рисунок 18: Часова залежність співвідношення Пуассона для ПВХ при 75\(^{\circ} C\), припускаючи в'язкопружний зсув і пружний гідростатичний відгук.
У разі ізотропії матеріалу (властивості, що не залежать від напрямку вимірювання), для повної характеристики матеріалу знадобляться не більше двох в'язкопружних операторів\(\mathcal{K}\) — скажімо,\(\mathcal{G}\) і —. Для матеріалів, що демонструють нижчі порядки симетрії, знадобиться більше дескрипторів: поперечно-ізотропний матеріал вимагає чотирьох складових дескрипторів, ортотропний матеріал - дев'ять, а триклінічний - двадцять один. Якщо матеріал є одночасно в'язкопружним і анізотропним, це кількість в'язкопружних операторів, які будуть потрібні. Зрозуміло, що аналітик повинен бути проникливим у пошуку належного балансу між реалістичністю і практичністю у виборі моделей.
5.2 Суперпозиція
На щастя, часто непотрібно починати з нуля у вирішенні завдань будівельної механіки, які стосуються в'язкопружних матеріалів. Ми виділимо два зручних методу адаптації стандартних рішень для лінійних пружних матеріалів до в'язкопружного випадку, і перший з них заснований на принципі суперпозиції Больцмана. Ми проілюструємо це на конкретному прикладі тонкостінного посудини під тиском.
Полімери, такі як полібутилен та полівінілхлорид, знаходять все більш широке застосування в сантехніці та інших системах подачі рідини, і ці матеріали виявляють вимірну в'язкопружну залежність часу в їх механічній реакції. Зазвичай ігнорувати ці ефекти швидкості при проектуванні простих систем, використовуючи щедрі фактори безпеки. Однак у більш критичних ситуаціях дизайнер може побажати розширити теорію пружності, викладену в стандартних текстах, включивши в'язкопружність матеріалу.
Одним з важливих моментів для напруги на початку є те, що в багатьох випадках розподіл напружень не залежить від властивостей матеріалу і, отже, не залежить від в'язкопружності. Наприклад, напруга «обруча»\(\sigma_{\theta}\) у відкритому циліндричному посудині під тиском є
\(\sigma_{\theta} = \dfrac{pr}{b}\)
де\(p\) - внутрішній тиск,\(r\) - радіус посудини, і\(b\) товщина стінки. Якщо матеріал виявляється в'язкопружним, це співвідношення - яке не містить матеріальних констант - застосовується без змін.
Однак на переміщення - наприклад, збільшення радіуса\(\delta_r\) - впливають, збільшуючись з часом, коли деформація в матеріалі збільшується через молекулярну конформаційну зміну. Для відкритого циліндричного резервуара з лінійним еластичним матеріалом радіальне розширення
\(\delta_r = \dfrac{pr^2}{bE}\)
Модуль пружності в знаменнику вказує на те, що радіальне розширення буде збільшуватися, оскільки матеріал втрачає жорсткість через в'язкопружну реакцію. При кількісному оцінці такої поведінки зручно замінити модуль\(E\) відповідністю\(C = 1/E\). Вираз для радіального розширення тепер має матеріальну константу в чисельнику:
\[\delta_r = \dfrac{pr^2}{b} C\]
Якщо тиск\(p\) постійний, в'язкоеластичність входить в проблему тільки через відповідність матеріалу\(C\), який повинен бути виконаний відповідною залежною від часу функцією. (Тут ми припускаємо, що значення\(r\) і\(b\) можуть розглядатися як константа, яка, як правило, буде дійсною для хорошого наближення.) Значення\(\delta_r\) часу\(t\) - це просто коефіцієнт, що\((pr^2/b)\) помножує значення\(C(t)\) на той час.
Функція,\(C(t)\) необхідна тут, - це відповідність матеріалу повзучості, залежне від часу деформація, що проявляється матеріалом у відповідь на нав'язане одиничне напруження при розтягуванні:\(C_{crp} = \epsilon (t)/\sigma_0\). Стандартне лінійне тверде тіло, задане рівнянням 5.4.30, дає відповідність як
\[C_{crp} (t) = C_g + (C_r - C_g) (1 - e^{-t/\tau})\]
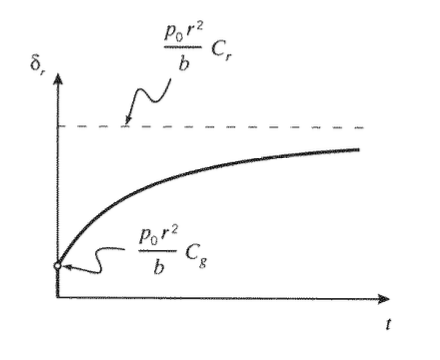
де тут передбачається, що напруга прикладається під час\(t = 0\). Радіальне розширення посудини під тиском, що піддається постійному внутрішньому тиску\(p_0\) і побудоване з матеріалу, для якого S.L.S. є розумною моделлю,
\[\delta_r (t) = \dfrac{p_0 r^2}{b} [C_g + (C_r - C_g) (1 - e^{-t/\tau}]\]
Ця функція схематично показана на малюнку 19.
Ситуація трохи складніше, якщо і внутрішній тиск, і відповідність матеріалу залежать від часу. Некоректно просто використовувати вищевказане рівняння зі значенням\(p_0\) заміненого значенням\(p(t)\) в довільний час, тому що на радіальне розширення в часі\(t\) впливає тиск в попередні часи, а також тиск в поточний час.
Правильна процедура полягає в тому, щоб «скласти» функції тиску та відповідності разом у інтегралі згортки, як це було зроблено при розробці принципу суперпозиції Больцмена. Це дає:
\[\delta_r (t) = \dfrac{r^2}{b} \int_{-\infty}^t C_{crp} (t - \xi) \dot{p} (\xi) d\xi\]
Приклад\(\PageIndex{13}\)
Нехай внутрішній тиск буде постійно зростаючою функцією «рампи»\(p = R_pt\), так що,\(R_p\) будучи темпом збільшення; тоді у нас є\(\dot{p} (\xi) = R_p\). Використовуючи стандартне лінійне тверде тіло рівняння 5.4.55 для відповідності повзучості, напруга обчислюється з інтеграла згортки як
Ця функція побудована на малюнку 20, для гіпотетичного матеріалу з параметрами\(C_g = 1/3 \times 10^5 \text{ psi}^{-1}\),,,\(C_r = 1/3 \times 10^4 \text{ psi}^{-1}\)\(b = 0.2\ in\)\(r = 2 \ in\),\(\tau = 1\) місяць і\(R_p = 100\) psi/місяць. Зверніть увагу, що швидкість повзучості збільшується від початкового значення\((r^2/b)R_pC_g\) до кінцевого значення\((r^2/b)R_pC_r\), оскільки склоподібні еластичні компоненти розслабляються.
Малюнок 20: Повзучість\(\delta_r(t)\) гіпотетичного посудини під тиском для постійно зростаючого внутрішнього тиску.
Коли посудина під тиском має закриті кінці і, отже, повинен протистояти осьовим, а також напруженням обруча, радіальне розширення є\(\delta_r = (pr^2/bE) [1 − (ν/2)]\). Розширення цього відношення до реакції в'язкопружного матеріалу та тиску, що залежить від часу, є ще одним кроком у складності. Тепер два дескриптори матеріалу,\(E\) і\(ν\), повинні бути змодельовані відповідними залежними від часу функціями, а потім скласти в функцію тиску. Описаний вище підхід суперпозиції може бути використаний і тут, але з більшою алгебраїчною складністю. «Принцип в'язкопружної відповідності», який буде представлений нижче, часто є більш простим, але концепція суперпозиції дуже важлива для розуміння реакції матеріалів, що залежать від часу.
5.3 Принцип в'язкопружного відповідності
У пружних матеріалах граничні тяги та зсуви можуть залежати від часу, а також положення, не впливаючи на розв'язання: час переноситься лише як параметр, оскільки в керуючих рівняннях не з'являються похідні часу. З в'язкопружними матеріалами конститутивне або напружено-деформоване рівняння замінюється на диференціальне за часом рівняння, що ускладнює подальше розв'язання. Однак у багатьох випадках польові рівняння мають певні математичні властивості, які дозволяють відносно легко отримати рішення (E.H. Lee, «В'язкопружність», Довідник з інженерної механіки, W. Flugge, ред., Макгроу-Хілл, Нью-Йорк, 1962, глава 53.). «Принцип в'язкопружної відповідності», який буде викладено тут, працює шляхом адаптації раніше доступного еластичного розчину, щоб зробити його застосовним і до в'язкопружних матеріалів, так що нове рішення з нуля є непотрібним.
Якщо механічна задача - структура, її матеріали та граничні умови тяги та переміщення - піддається перетворенню Лапласа, часто трапляється так, що жодна з просторових аспектів її опису не буде змінена: проблема буде виглядати однаковою, принаймні просторово. Тільки залежні від часу аспекти, а саме властивості матеріалу, будуть змінені. Потім плоску версію задачі Лапласа можна інтерпретувати як представляє задачу аналізу напружень для пружного тіла тієї ж форми, що і в'язкопружне тіло, так що розв'язок пружного тіла буде застосовуватися і до відповідного в'язкопружного тіла, але в площині Лапласа.
Однак є виняток із цієї відповідності: хоча фізична форма тіла незмінна при переході до площини Лапласа, граничні умови тяги або переміщення можуть бути змінені просторово при перетворенні. Наприклад, якщо накладена тяга є\(\hat{T} = \cos (xt)\), то\(\bar{\hat{T}} = s/(s^2 + x^2)\); це, очевидно, іншої просторової форми, ніж оригінал
нетрансформована функція. Однак функції, які можуть бути записані як розділені фактори простору та часу, не змінюватимуться просторово при перетворенні:
\(\hat{T} (x, t) = f(x) g(t) \Rightarrow \bar{\hat{T}} = f(x) \bar{g}(s)\)
Це означає, що проблеми аналізу напружень, граничні обмеження яких не залежать від часу або в гіршому випадку є відокремленими функціями простору та часу, будуть виглядати однаково як у фактичній, так і в площині Лапласа. У площині Лапласа проблема геометрично ідентична «асоційованої» пружної задачі.
Зводячи в'язкопружну задачу до асоційованої пружної шляхом прийняття перетворень, може бути використана велика бібліотека пружних розв'язків: шукають розв'язку пов'язаної пружної задачі, а потім виконують інверсію Лапласа для повернення до площини часу. Процес аналізу в'язкопружних напружень з використанням методів перетворення зазвичай називають «принципом відповідності», який можна констатувати у вигляді наступного рецепту:
1. Визначте природу пов'язаної пружної задачі. Якщо просторовий розподіл граничних і тіло-силових умов незмінно при перетворенні - звичайному явищі - то пов'язана пружна задача постає точно так само, як вихідна в'язкопружна.
2. Визначте рішення цієї пов'язаної пружної задачі. Це часто можна зробити за допомогою посилання на стандартні довідники (наприклад, В.С. Янг, Формули Roark для стресу і деформації, McGraw-Hill, Inc., Нью-Йорк, 1989.) або текстів з теорії пружності (наприклад, С.Тимошенко і J.N. Goodier, Theory of Elasticity, McGraw-Hill, Inc., Нью-Йорк, 1951.).
3. Переформувати пружні константи, що виникають у пружному розчині, в терміні придатних в'язкопружних операторів. Як обговорювалося в розділі 5.1, часто зручно замінювати\(E\) і\(ν\) на\(G\) і\(K\), а потім замінити\(G\) і\(K\) на їх в'язкопружні аналоги:
\(\left \{ \begin{array} {c} E \\ v \end{array} \right \} \to \begin{cases} G \to \mathcal{G} \\ K \to \mathcal{K} \end{cases}\)
- Замініть застосовані граничні та тілесні силові обмеження на їх перетворені аналоги:
\(\hat{T} \Rightarrow \bar{\hat{T}}\)
\(\hat{u} \Rightarrow \bar{\hat{u}}\)
де\(\hat{T}\) і\(\hat{u}\) накладаються тяги і зсуви відповідно.
5. Інвертуйте отриманий таким чином вираз, щоб отримати розв'язку в'язкопружної задачі в часовій площині.
Якщо пружний розчин містить лише дві залежні від часу величини в чисельнику, такі як у Рівнянні 5.4.54, принцип відповідності еквівалентний методу суперпозиції попереднього розділу. На прикладі напірної посудини метод відповідності дає
\(\delta_r = \dfrac{pr^2 C}{b} \to \bar{\delta}_r (s) = \dfrac{r^2}{b} \bar{p} \mathcal{C}\)
Оскільки\(\mathcal{C} = s \bar{C}_{crp}\) відношення перетворення для інтегралів згортки дає
як і раніше. Однак принцип відповідності є більш простим у задачах, що мають складне поєднання залежних від часу функцій, як показано в наступному прикладі.
Приклад\(\PageIndex{14}\)
Еластичним рішенням для радіального розширення закритого циліндричного посудини під тиском радіуса\(r\) і товщини\(b\) є
Дотримуючись рецепту принципу відповідності, пов'язаний розчин в площині Лапласа
З точки зору гідростатичної та зсувної функцій реагування в'язкопружними операторами є:
\(\mathcal{E} (s) = \dfrac{9\mathcal{G} (s) \mathcal{K} (s)}{3 \mathcal{K} (s) + \mathcal{G} (s)}\)
У прикладі розглянуто матеріал ПВХ при 75\(\PageIndex{12}\),\(^{\circ}C\) який до хорошого наближення був еластичним у гідростатичному відгуку і в'язкопружним при зсуві. Використовуючи стандартну лінійну тверду модель, ми мали
\(\mathcal{K} = K_e, \ \ \ \mathcal{G} = G_r + \dfrac{(G_g - G_r)s}{s + \tfrac{1}{\tau}}\)
де\(K_e =1.33\)\(G_g =800\) ГПа, МПа,\(G_r =1.67\) МПа, і\(\tau =100\) с.
Для постійного внутрішнього тиску\(p(t) = p_0\),\(\bar{p} = p_0/s\). Всі ці вирази необхідно об'єднати, а результат інвертувати. Команди Maple для цієї проблеми можуть бути:
define shear operator > G:=Gr+((Gg-Gr)*s)/(s+(1/tau)); define Poisson operator > N:=(3*K-2*G)/(6*K+2*G); define modulus operator > Eop:=(9*G*K)/(3*K+G); define pressure operator > pbar:=p0/s; get d1, radial displacement (in Laplace plane) > d1:=(pbar*r^2)*(1-(N/2))/(b*Eop); read Maple library for Laplace transforms > readlib(inttrans); invert transform to get d2, radial displacement in real plane > d2:=invlaplace(d1,s,t);
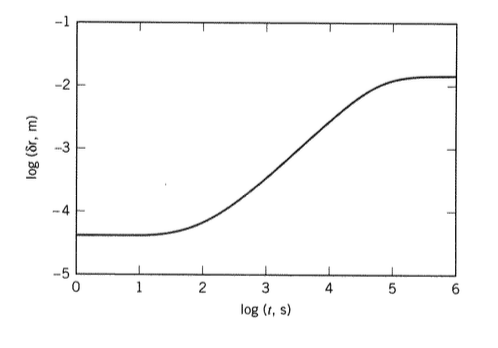
Після деякої ручної перестановки радіальне зміщення\(\delta_r(t)\) можна записати у вигляді
де час затримки повзучості\(\tau_c = \tau (G_g/G_r)\). Продовження сеансу Maple:
define numerical parameters > Gg:=800*10^6; Gr:=1.67*10^6; tau:=100; K:=1.33*10^9; > r:=.05; b:=.005; p0:=2*10^5; resulting expression for radial displacement > d2; - .01494 exp( - .00002088 t) + .01498
Графік log-log цієї функції показаний на малюнку 21. Зауважимо, що для цієї задачі ефект невеликої зміни коефіцієнта Пуассона\(ν\) під час переходу є незначним порівняно з дуже великою зміною модуля\(E\), так що майже ідентичний результат був би отриманий просто шляхом дозволу\(ν\) = константа = 0,5. З іншого боку, не помітно складніше включити залежність від часу,\(ν\) якщо є програмне забезпечення для символічних маніпуляцій.
6. Додаткові посилання
- Аклоніс, Дж., Макнайт, В.Дж., і Шен, М., Вступ до полімерної в'язкопружності, Wiley-Interscience, Нью-Йорк, 1972.
- Крістенсен, Р.М., Теорія в'язкопружності, 2-е видання, Академічна преса, Нью-Йорк, 1982.
- Феррі, Дж., В'язкопружні властивості полімерів, 3-е видання, Wiley & Sons, Нью-Йорк, 1980.
- Авіаквитки, В., В'язкопружність, Спрінгер-Верлаг, Нью-Йорк, 1975.
- Маккрам, Н.Г., Читати, B.E., і Williams, G., Апружні та діелектричні в полімерних твердих тілах, Wiley & Sons, Лондон, 1967. Доступно з Dover Publications, Нью-Йорк.
- Tschoegl, N.W., Феноменологічна теорія лінійної в'язкопружної поведінки, Спрінгер-Верлаг, Гейдельберг, 1989.
- Tschoegl, N.W., «Часова залежність у властивостях матеріалів: огляд», Механіка залежних від часу матеріалів, Том 1, с. 3—31, 1997.
- Вільямс, М.Л., «Структурний аналіз в'язкопружних матеріалів», Журнал AIAA, стор. 785, травень 1964.
Вправа\(\PageIndex{1}\)
Побудувати функції\(e^{-t/\tau}\) і\(1 - e^{t/\tau}\) проти\(\log_10 t\) від\(t = 10^{-2}\) до\(t= 10^2\). Мають дві криві на графіку для кожної функції, одну для\(\tau = 1\) та одну для\(\tau = 10\).
Вправа\(\PageIndex{2}\)
Визначте уявну енергію активації в (\(E^{\dagger}\)в рівнянні 5.4.2) для в'язкопружної релаксації, в якій початкова швидкість спостерігається вдвічі при підвищенні температури від 20\(^{\circ} C\) до 30\(^{\circ} C\). (Відповідь:\(E^{\dagger} = 51\ kJ/mol\).)
Вправа\(\PageIndex{3}\)
Визначте щільність\(N\) зшивання і молекулярну масу сегмента\(M_c\) між зшивними зв'язками для гуми з початковим модулем\(E = 1000\) psi at\(20^{\circ}C\) і щільністю\(1.1 \ g/cm^3\). (Відповідь:\(N = 944\ mol/m^3, M_c = 1165\ g/mol\).)
Вправа\(\PageIndex{4}\)
Розгорніть експоненціальні форми для динамічного напруження та деформації (\(\sigma (t) = \sigma_0^* e^{i\omega t}, \epsilon (t) =\epsilon_0^* e^{i\omega t}\)) і покажіть, що
\(E^* = \dfrac{\sigma(t)}{\epsilon (t)} = \dfrac{\sigma_0 \cos \delta}{\epsilon_0} + i\dfrac{\sigma_0 \sin \delta}{\epsilon_0}\),
де\(\delta\) - фазовий кут між напругою і деформацією.
Вправа\(\PageIndex{5}\)
Використовуючи співвідношення\(\bar{\sigma} = \mathcal{E} \bar{\epsilon}\) для випадку динамічного навантаження (\(\epsilon (t) = \epsilon_0 \cos \omega t\)) та реакції матеріалу S.L.S.\(\left(\mathcal{E} = k_e + k_1s/(s + \tfrac{1}{\tau})\right)\), розв'яжіть залежне від часу напруження\(\sigma (t)\). Використовуйте це рішення для ідентифікації стаціонарних компонентів комплексного модуля\(E^* = E' + iE''\), а також перехідної складової. Відповідь:
Вправа\(\PageIndex{6}\)
Для стандартного лінійного твердого тіла з параметрами\(k_e = 25\)\(k_1 = 50\), і\(\tau_1 = 1\), графік\(E'\) і\(E''\) проти\(\log \omega\) в діапазоні\(10^{-2} < \omega \tau_1 < 10^2\). Також графік\(E''\) проти\(E'\) в цьому ж діапазоні, використовуючи звичайні, а не логарифмічні осі та однакову шкалу для обох осей (діаграма Арганда).
Вправа\(\PageIndex{7}\)
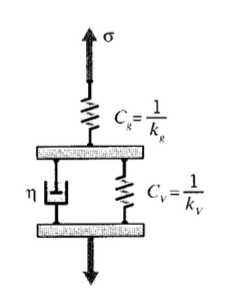
Показати, що в'язкопружний закон для форми «Фойгта» стандартного лінійного твердого тіла (пружини жорсткості\(k_v = 1/C_v\) паралельно з приладом в'язкості\(eta\), і це поєднання послідовно з іншою пружиною жорсткості\(k_g = 1/C_g\)) може бути написано
\(\bar{\epsilon} = \mathcal{C} \bar{\sigma}, \text{ with } \mathcal{C} = \left [C_g + \dfrac{C_v}{\tau(s + \tfrac{1}{\tau})} \right ] \)
де\(\tau = \eta /k_v\).
Вправа\(\PageIndex{8}\)
Показати, що відповідність повзучості моделі Voigt SLS вправи\(\PageIndex{7}\) є
Вправа\(\PageIndex{9}\)
У випадках, коли прописується напруга, а не деформація, модель Кельвіна - послідовне розташування елементів Фойгта - краще моделі Віхерта:
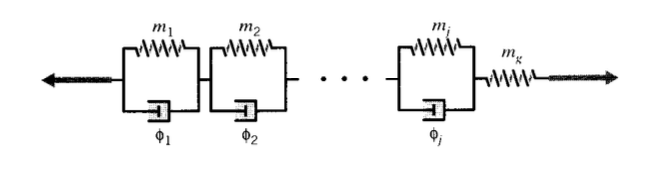
де\(\phi_j = 1/\eta_j = \dot{\epsilon}_j/\sigma_{dj}\) і\(m_j = 1/k_j = \epsilon_j/\sigma_{sj}\) Використовуючи відносини\(\epsilon = \epsilon_g + \sum_j \epsilon_j\),\(\sigma = \sigma_{sj} + \sigma_{dj}\)\(\tau_j = m_j /\phi_j\), показати пов'язане в'язкопружне складове рівняння бути:
\(\bar{\epsilon} = \left [m_g + \sum_j \dfrac{m_j}{\tau_j (s + \tfrac{1}{\tau_j})} \right ] \bar{\sigma}\)
і для цієї моделі показати відповідність повзучості бути:
Вправа\(\PageIndex{10}\)
Для простої моделі Voigt (\(C_g = 0\)у Вправі\(\PageIndex{7}\)), показати, що деформація\(\epsilon^{t + \Delta t}\) в часі\(t + \Delta t\) може бути записана з точки зору деформації\(\epsilon^t\) в часі\(t\) і напруга, що\(\sigma^t\) діє під час приросту часу\(\Delta t\) як
Використовуйте цей алгоритм для побудови деформації повзучості, що виникає внаслідок постійного напруження\(\sigma = 100\) проти\(\log t =(1, 5)\) for\(C_v = 0.05\) і\(\tau = 1000\).
Вправа\(\PageIndex{11}\)
Побудувати реакцію деформації\(\epsilon (t)\) на вхідні навантаження навантаження навантаження, визначені як
\(\sigma (t) = \begin{cases} 0, & t < 1 \\ 1, & 1 < t < 4.5 \\ -1, & 4.5 < t < 5 \\ 0, & t > 5 \end{cases}\)
Матеріал підпорядковується закону відповідності SLS (рівняння 5.4.30) з\(C_g = 5, C_r = 10\), і\(\tau = 2\).
Вправа\(\PageIndex{12}\)
Використання форми Максвелла стандартного лінійного твердого тіла з\(k_e = 10, k_1 = 100\) і\(\eta = 1000\):
а) Ділянка\(E_{rel} (t)\) і\(E_{crp} (t) = 1/C_{crp} (t)\) проти часу журналу.
б) Ділянка\([E_{crp}(t) - E_{rel}(t)]\) проти довгого часу.
в) Порівняйте час релаксації з часом затримки (час, коли аргумент експоненції стає -1, для розслаблення і повзучості відповідно). Розмірковуйте, чому одне коротше іншого.
Вправа\(\PageIndex{13}\)
Показати, що модель Віхерта з двома плечами Максвелла (рівняння 5.4.34) еквівалентна звичайному диференціальному рівнянню другого порядку
\(a_2 \ddot{\sigma} + a_1 \dot{\sigma} + a_0 \sigma = b_2 \ddot{\epsilon} + b_1 \dot{\epsilon} + b_0 \epsilon\)
де
\(a_2 = \tau_1 \tau_2, \ \ \ \ a_1 = \tau_1 + \tau_2, \ \ \ \ a_0 = 1\)
\(b_2 = \tau_1 \tau_2 (k_e + k_1 + k_2), \ \ \ \ b_1 = k_e (\tau_1 + \tau_2) + k_1 \tau_1 + k_2 \tau_2, \ \ \ \ b_0 = k_e\)
Вправа\(\PageIndex{14}\)
Для в'язкопружного матеріалу, визначеного диференціальним складовим рівнянням:
\(15 \ddot{\sigma} + 8 \dot{\sigma} = \sigma = 105 \ddot{\epsilon} + 34 \dot{\epsilon} + \epsilon\),
написати вираз для модуля релаксації у вигляді серії Проні (Рівняння 5.4.36). (Відповідь:\(E_{rel} = 1 + 2e^{-t/3} + 4e^{-t/5}\))
Вправа\(\PageIndex{15}\)
Для простого елемента Максвелла переконайтеся, що
Вправа\(\PageIndex{16}\)
Оцініть інтеграл Больцмана
визначити реакцію стандартного лінійного твердого тіла на синусоїдальне напруження\((\epsilon (t) = \cos (\omega t))\)
Вправа\(\PageIndex{17}\)
Вивести рівняння 5.4.48, використовуючи вираз Арреніуса для часу релаксації, щоб відняти час релаксації журналу при довільній температурі\(T\) від температури при опорній температурі\(T_{ref}\).
Вправа\(\PageIndex{18}\)
Використовуючи дані ізотермічної релаксації напружень при різних температурах, коефіцієнти зсуву були виміряні для поліуретанового матеріалу, як показано в таблиці нижче:
| \(T, ^{\circ} C\) | \(\log_{10} a_T\) |
| +5 | -0.6 |
| 0 | 0 |
| -5 | 0.8 |
| -10 | 1,45 |
| -15 | 2.30 |
| -20 | 3.50 |
| -25 | 4.45 |
| -30 | 5.20 |
(а) Ділянка\(\log a_T\) проти\(1/T (^{\circ} K)\); обчислити середню енергію активації за допомогою Eqn 5.4.48. (Відповідь:\(E^{\dagger} = 222 kJ/mol\).)
(б) Графік\(\log a_T\) проти\(T(^{\circ} C)\) і порівняйте з рівнянням WLF (Рівняння 5.4.50), с\(T_g = -35^{\circ} C\). (Зауважте, що\(T_{ref} = 0 \ne T_g\).)
Вправа\(\PageIndex{19}\)
Після зсуву часової температури головна крива релаксації при 0\(^{\circ} C\) для поліуретану вправи\(\PageIndex{18}\) дає наступні значення\(E_{rel} (t)\) в різний час:
| \(\log (t, min)\) | \(E_{rel} (t)\), фунтів на квадратний дюйм |
| -6 | 56 280 |
| -5 | 22 880 |
| -4 | 4 450 |
| -3 | 957 |
| -2 | 578 |
| -1 | 481 |
| 0 | 480 |
(a) У Рівнянні 5.4.36 виберіть\(k_e = E_{rel} (t = 0) = 480\).
(b) Виберіть значення\(\tau_j\), які відповідають часу, вказаному у наведеній вище таблиці від\(10^{-6}\) до\(10^{-1}\) (процес, який називається «collocation»).
(c) Визначте відповідні значення жорсткості пружини, що\(k_j\) відповідають кожній з них,\(\tau_j\) щоб рівняння 5.4.36 відповідала експериментальним значенням\(E_{rel} (t)\). Це можна зробити, встановивши і вирішивши послідовність лінійних алгебраїчних рівнянь\(k_j\) з невідомими:
Зверніть увагу, що матриця коефіцієнтів по суті трикутна, що полегшує ручне рішення в разі, якщо комп'ютер недоступний.
(d) Відрегулюйте значення\(k_1\) так, щоб сума всіх пружин жорсткості дорівнювала склоподібному модулю\(E_g = 91,100\) psi.
(e) Побудувати модуль релаксації, передбачений моделлю від 0\(\log t = -8\) до 0.
Вправа\(\PageIndex{20}\)
Побудуйте значення релаксації (постійної деформації) модуля\(E\) і коефіцієнта\(ν\) Пуассона для поліізобутилену, дилатаційна і зсувна реакція якого показані на малюнку 17. Припустимо, моделі S.L.S. як для дилатації, так і для зсуву.
Вправа\(\PageIndex{21}\)
Пружний розчин напруги\(\sigma_x (x,y)\) і вертикального прогину\(v(x,y)\) в консольній балці довжини\(L\) і моменту інерції\(I\), навантаженої на вільному кінці силою\(F\), становить
Визначте в'язкопружні аналоги цих відносин за допомогою методів суперпозиції та відповідності, припускаючи поведінку S.L.S. для відповідності матеріалу (Рівняння 5.4.30).
Вправа\(\PageIndex{22}\)
Полімер з в'язкопружними властивостями, як наведено на рис. 17, поміщають в жорстку кругову матрицю і навантажують тиском\(\sigma_y = 1\) МПа. Покладіть поперечне напруження\(\sigma_x (t)\) та осьове напруження\(\epsilon_y (t)\)\(\log t = -5\) до 1. Еластичним розчином є
