5.2: Експериментальні рішення

Вступ

Як було видно з попередніх модулів, аналіз напружень навіть простої геометрії може призвести до складного математичного маневрування. Актуальні вироби — колінчасті вали двигуна, медичні протези, тенісні ракетки тощо — мають граничні форми, які неможливо легко описати математично, і навіть якби вони були, було б вкрай важко підлаштувати до них рішення керуючих рівнянь. Одним із підходів до цього глухого кута є експериментальний, в якому ми прагнемо побудувати фізичну лабораторну модель, яка якимось чином виявляє напруження вимірним способом.

Це характер сил і стресів, які вони не можуть бути виміряні безпосередньо. Це ефект сили, який можна виміряти: коли ми зважуємо об'єкт за весняною шкалою, ми фактично вимірюємо розтягнення пружини, а потім обчислюємо силу за законом Гука. Експериментальний стресовий аналіз, таким чином, насправді є експериментальним деформаційним аналізом. Складність полягає в тому, що деформації в лінійному пружному режимі майже завжди невеликі, близько 1% або менше, і мистецтво в цій галузі полягає у виявленні та інтерпретації малих переміщень. Ми шукаємо явища, які демонструють великі та вимірювані зміни внаслідок малих та важко виміряних переміщень. Існує ряд таких прийомів, і три з них будуть викладені коротко у в наступних розділах. Багато методології було розроблено навколо цих та інших експериментальних методів, і як подальше читання (Посібник з експериментального аналізу стресу, третє видання, Товариство експериментального аналізу стресу (нині Товариство експериментальної механіки), 1978.) і лабораторна практика буде потрібно поставити стати компетентний в цій сфері.

тензометричні

Термін «тензодатчик» зазвичай позначає тонкий дріт або фольгу, складену взад-вперед на собі і прикріплену до поверхні зразка, як показано на малюнку 1, яка здатна генерувати електричну міру деформації в зразку. Коли провід розтягується разом зі зразком, електричний опір дроту\(R\) змінюється як через те, що його довжина\(L\) збільшується, так і площа поперечного перерізу\(A\) зменшується. Для багатьох резисторів ці змінні пов'язані простим виразом, виявленим в 1856 році лордом Кельвіном:

\(R = \dfrac{\rho L}{A}\)

Малюнок 1: Тензодатчик опору дроту.

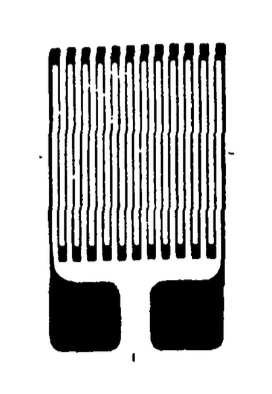
де\(\rho\) ось питомий опір матеріалу. Щоб висловити вплив деформації\(\epsilon = dL/L\) в довгому напрямку проводу на електричний опір, припустимо круглий провід з\(A = \pi r^2\) і візьмемо логарифми:

Загальний диференціал цього виразу дає

Так як

\(\epsilon_r = \dfrac{dr}{r} = -v \dfrac{dL}{L}\)

потім

\(\dfrac{dR}{R} = \dfrac{d \rho}{\rho} (1 + 2v) \dfrac{dL}{L}\)

П.У. Бріджман (1882 - 1961) у 1929 році вивчив вплив зміни об'єму на електричний опір і виявив, що вони змінюються пропорційно:

\[\dfrac{d\rho}{\rho} = \alpha_R \dfrac{dV}{V}\]

де\(\alpha_R\) - константа пропорційності між зміною опору та зміною обсягу. Записуючи зміну гучності з точки зору зміни довжини і площі, це стає

Звідси

\[\dfrac{dR/R}{\epsilon} = (1 + 2v) + \alpha_R (1 - 2v)\]

Ця величина називається коефіцієнтом gage, GF. Константан, 45/55 нікель/мідний сплав, має\(\alpha_R = 1.13\) і\(v = 0.3\), даючи\(GF \approx 2.0\). Цей матеріал також має низький температурний коефіцієнт питомого опору, що знижує температурну чутливість тензодатчика.

Малюнок 2: Мостова схема Уїтстона для тензодатчиків.

Зміна опору лише 2%, яка генерується датчиком з напругою\(GF = 2\) 1%, не була б помітна на простому омметрі. З цієї причини тензодатчики майже завжди підключені до схеми моста Уїтстона, як показано на малюнку 2. Ланцюг можна регулювати за допомогою змінного опору\(R_2\) для отримання нульової вихідної напруги\(V_{out}\) перед подачею деформації на датчик. Зазвичай опір датчика становить приблизно 350,\(\Omega\) а напруга збудження близько\(10V\). Коли опір датчика змінюється деформацією, міст незбалансований, і на виході з'являється напруга відповідно до співвідношення

\(\dfrac{V_{out}}{V_{in}} = \dfrac{\Delta R}{2R_0}\)

де\(R_0\) - номінальний опір чотирьох мостових елементів. Вихідна напруга легко вимірюється, оскільки це відхилення від нуля, а не є відносно невеликою зміною, накладеною на набагато більшу кількість; таким чином, вона може бути посилена відповідно до потреб системи збору даних.

Температурна компенсація може бути досягнута шляхом виготовлення мостового елемента на протилежній стороні моста від активного датчика, скажімо\(R_3\), неактивного калібру, який розміщений поблизу активного датчика, але не прив'язаний до зразка. Зміни опору в активному датчику через температуру потім будуть зміщені рівною зміною опору в іншому плечі моста.

Малюнок 3: Скасування ефектів згинання.

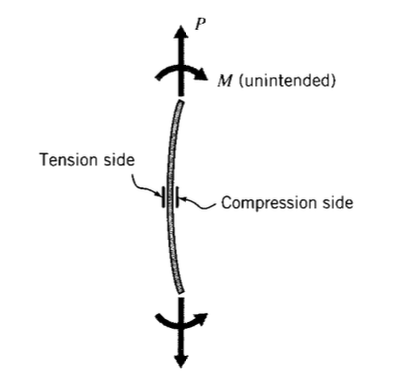
Часто важко встановити розтяжний зразок у випробувальній машині, не ненавмисно застосовуючи вигин на додаток до навантажень на розрив. Якби один калібр був застосований до опуклої зовнішньої сторони зразка, його показання було б помилково високим. Аналогічно, калібр, розміщений на увігнутій всередину або стискаючій стороні, буде читати низько. Ці помилки згинання можна усунути, використовуючи активний датчик на кожній стороні зразка, як показано на малюнку 3, і проводите їх на тій же стороні моста Уїтстоуна, наприклад\(R_1\) і\(R_4\). Розтяжна складова вигину на одній стороні зразка супроводжується рівним, але стискаючим компонентом з іншого боку, і вони будуть генерувати рівні, але протилежні зміни опору в\(R_1\) і\(R_4\). Ефект вигину, отже, скасовується, а комбінація калібру вимірюватиме лише напругу на розтяг (з подвоєною чутливістю, оскільки обидва\(R_1\) і\(R_4\) активні).

Малюнок 4: Розетку процідити.

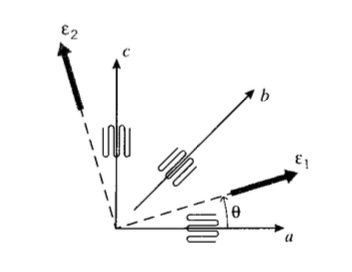
Деформацію в напрямку датчика можна знайти безпосередньо з коефіцієнта датчика (Рівняння 5.2.1). Коли напрямок основного напруги невідомий, корисні тензометричні розетки; вони використовують кілька датчиків на одній плівковій основі, орієнтованих в різні боки. Прямокутна триколірна розетка, показана на малюнку 4, використовує два датчики, орієнтовані перпендикулярно, і третій калібр, орієнтований на 45\(^{\circ}\) до перших двох.

Приклад\(\PageIndex{1}\)

Триколірна розетка дає показання\(\epsilon_0 = 150\mu\)\(\epsilon_{45} = 200 \mu\), причому\(\epsilon_{90} = -100 \mu\) (тут\(\mu\) символ позначає мікрометри на метр). Якщо ми вирівнюємо\(\epsilon_y\) вісь\(\epsilon_x\) і вздовж напрямків 0\(^{\circ}\)\(^{\circ}\) і 90 калібру, то\(\epsilon_x\) і\(\epsilon_y\) вимірюються безпосередньо, так як це\(\epsilon_0\) і\(\epsilon_{90}\) відповідно. Для визначення деформації зсуву скористаємося правилом перетворення деформації\(\gamma_{xy}\), щоб записати нормальну деформацію при 45\(^{\circ}\):

\(\epsilon_{45} = 200\mu = \epsilon_{x} \cos^2 45 + \epsilon_y \sin^2 45 + \gamma_{xy} \sin 45 \cos 45\)

Підставляючи відомі значення для\(\epsilon_x\) і\(\epsilon_y\), і розв'язуючи,

\(\gamma_{xy} = 350 \mu\)

Основні штами тепер можна знайти як

Кут від\(x\) -осі до головної площини дорівнює

Напруження можна знайти за деформаціями з матеріальних складових відносин; наприклад, для сталі з\(E = 205\) ГПа, а\(ν = .3\) головним напруженням є

Для конкретного випадку розетки 0-45-90 орієнтація головної осі деформації може бути задана безпосередньо за допомогою (М. Hetenyi, ред., Довідник з експериментального аналізу напружень, Wiley, Нью-Йорк, 1950.)

\[\tan 2 \theta = \dfrac{2 \epsilon_b - \epsilon_a - \epsilon_c}{\epsilon_a - \epsilon_c}\]

і основними штамами є

\[\epsilon_{1, 2} = \dfrac{\epsilon_a + \epsilon_c}{2} \pm \sqrt{\dfrac{(\epsilon_a - \epsilon_b)^2 + (\epsilon_b - \epsilon_c)^2}{2}}\]

Графічні рішення, засновані на колах Мора, також корисні для зменшення вихідних даних датчиків.

Тензодатчики використовуються дуже широко, і критичні конструкції, такі як літальні апарати, можуть бути обладнані сотнями датчиків під час випробувань. Кожен датчик повинен бути ретельно прикріплений до конструкції та підключений двома його висновками до блоку кондиціонування сигналу, який включає джерело напруги збудження та міст Уїтстона. Це, очевидно, може бути основним інструментарієм, з автоматизованого збору даних та зменшення практичної необхідності.

Фотоеластичність

Тензодатчики опору дроту, ймовірно, є основним пристроєм, що використовується в експериментальному аналізі напружень сьогодні, але вони мають недолік моніторингу деформації лише в одному місці. Методи фотоеластичності та муару, які будуть викладені в наступних розділах, є більш складними в концепції та застосуванні, але мають можливість забезпечити повнопольові відображення розподілу деформацій. Інтуїтивне розуміння цих дисплеїв може бути настільки цінним, що може бути непотрібним перетворити їх на числові значення, хоча перетворення можна зробити за бажанням.

Малюнок 5: Поширення світла.

Фотоеластичність використовує властивість багатьох прозорих полімерів і неорганічних стекол, які називаються подвійним заломленням. Щоб пояснити це явище, нагадаємо визначення показника заломлення\(n\), який представляє собою відношення швидкості світла\(v\) в середовищі до такої у вакуумі\(c\):

\[n = \dfrac{v}{c}\]

Коли світловий промінь рухається в просторі (див. Рис. 5), його вектор електричного поля\(E\) коливається вгору і вниз з кутовою частотою\(\omega\) в нерухомій площині, що називається площиною поляризації пучка. (Довжина хвилі світла становить\(\lambda = 2\pi c/\omega\).) Дволучепреломляющий матеріал - це той, у якого показник заломлення залежить від орієнтації площини поляризації, а величина дволучепреломлення - різниця показників:

\(\Delta n = n_{\perp} - n_{\parallel}\)

де\(n_{\perp}\) і\(n_{\parallel}\) - показники заломлення на двох площинях. Ті дві площини, які виробляють максимум\(\Delta_n\), є основними оптичними площинами. Як показано на малюнку 6, подвійний лучепреломляющий матеріал можна розглядати спрощено як венеціанський жалюзі, який вирішує довільно орієнтований вектор електричного поля на дві компоненти, по одній на кожній з двох основних оптичних площин, після чого кожен компонент буде транзитувати матеріал з різною швидкістю відповідно до Рівняння 5.2.4. Два компоненти врешті-решт вийдуть з матеріалу, знову подорожуючи з тією ж швидкістю, але зміщуючись по фазі один від одного на суму, пов'язану з різницею в часі транзиту.

Малюнок 6: Венеціансько-сліпа модель двопроменезаломлення.

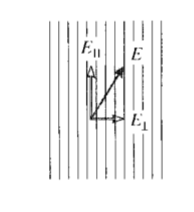
Фотопружний матеріал - це той матеріал, в якому подвійне заломлення залежить від прикладеного напруги, і багато таких матеріалів можуть бути описані до хорошого наближення напружено-оптичним законом

\[\Delta_n = C(\lambda) (\sigma_1 - \sigma_2)\]

де\(C\) - напружено-оптичний коефіцієнт, а величина в другій дужці - це різниця між двома основними напруженнями в площині, нормальній до напрямку поширення світла; це лише вдвічі більше максимального напруження зсуву в цій площині. Напружено-оптичний коефіцієнт, як правило, є функцією довжини хвилі\(\lambda\).

Розподіл напружень у тілі неправильної форми можна переглянути, відтворюючи фактичну структуру (ймовірно, збільшену або зменшену за розміром для зручності) у дволучепреломляючому матеріалі, такому як епоксидна смола. Якщо структура статично визначена, то напруги в моделі будуть такими ж, як і в реальній структурі, незважаючи на відмінності в модулі. Щоб зробити ефект подвійного заломлення видимим, модель розміщується між перехрещеними поляризаторами в апараті, відомому як полярископ. (Поляризатори, такі як Polaroid, полімерний лист, що містить орієнтовані кристали йодиду, по суті, просто двопроменезаломлюючі матеріали, які пропускають лише світло, поляризоване в головній оптичній площині поляризатора.)

Джерело випромінювання може виробляти як звичайний білий (поліхроматичний), так і відфільтрований (монохроматичний) світло. Вектор електричного поля світла, що вражає перший поляризатор з довільною орієнтацією, може бути розв'язаний на дві складові, як показано на малюнку 7, одна в напрямку поляризації, а інша перпендикулярна їй. Поляризатор заблокує поперечну складову, дозволяючи паралельному компоненту проходити до зразка. Цей поляризований компонент може бути записаний

Малюнок 7: Круговий полярископ.

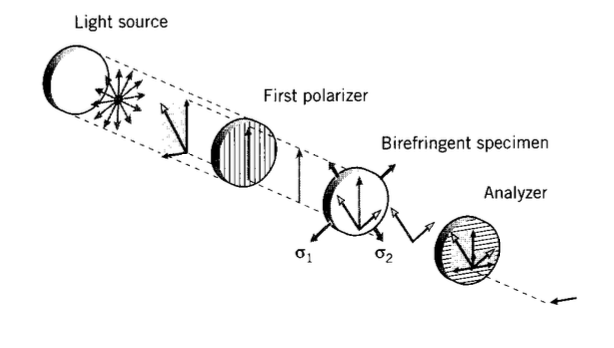
\(u_P = A \cos \omega t\)

де\(u_P\) - напруженість поля в часі\(t\). Дволучепреломляючий зразок розрішить цей компонент на два подальші компоненти, уздовж кожного з основних напрямів напруги; вони можуть бути записані як

\(u_1 = A \cos \alpha \cos \omega t\)

\(u_2 = A \sin \alpha \cos \omega t\)

де α - (невідомий) кут, який складає основні площини напружень з напрямком поляризації. Обидва ці нові компоненти проходять через зразок, але з різною швидкістю, заданою рівнянням 5.2.5. Проїхавши по зразку відстань\(h\) зі швидкостями\(v_1\) і\(v_2\), вони з'являються як

Ці два компоненти потім потрапляють на другий поляризатор, орієнтований на 90\(^{\circ}\) до першого і відомий як аналізатор. Кожен знову вирішується на подальші компоненти паралельно і перпендикулярно осі аналізатора, і перпендикулярні компоненти блокуються в той час як паралельні компоненти проходили через. Передана складова може бути записана як

\(u_A = -u_1' \sin \alpha + u_2' \cos \alpha\)

Це виду\(u_A = A' \sin (\omega t - \delta)\), де амплітуда і\(A'\)\(\delta\) є фазовим кутом. Зверніть увагу, що амплітуда дорівнює нулю, так що світло не буде передаватися, якщо\(\alpha = 0\) або якщо

\[\dfrac{2 \pi c}{\lambda} ( \dfrac{h}{2v_1} - \dfrac{h}{2v_2} ) = 0, \pi, 2\pi, \cdots\]

Випадок для якого\(\alpha = 0\) відбувається, коли основні площини напружень вирівнюються з осями поляризатор-аналізатор. Всі позиції на моделі, при яких це вірно, таким чином, виробляють згасання проданого світла. Вони розглядаються як темні смуги, які називаються ізоклініками, оскільки вони відображають лінії постійного нахилу головних осей напруги. Ці контури можна сфотографувати при послідовності поляризаційних орієнтацій, при бажанні, щоб дати ще більш повне уявлення про напрямки напружень.

Положення нульового напруження також спричиняють згасання, оскільки тоді затримка дорівнює нулю, а дві світлові компоненти, що виходять з аналізатора, скасовують один одного. Наприклад, нейтральна вісь променя при згинанні відображається як чорна лінія в спостережуваному полі. Оскільки напруга в даному місці збільшується з нуля, зростаюче зсув фаз між двома складовими призводить до того, що скасування буде неповним, і спостерігається світло. Врешті-решт, оскільки стрес ще більше збільшується, затримка досягне\(\delta = \pi\), і згасання відбудеться знову. Це створює ще одну темну бахрому в спостережуваному полі. Взагалі видно чергуються світлі ділянки та темні окантовки, що відповідає зростаючим порядкам вимирання.

Малюнок 8: Фотопружні візерунки для напруження навколо (а) круглого отвору і (б) гострої тріщини.

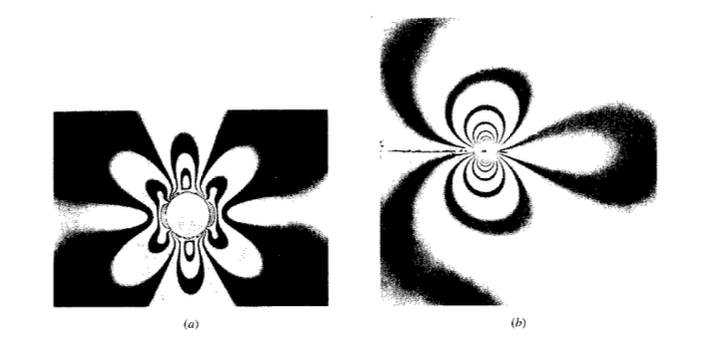
Близький інтервал бахроми вказує на крутий градієнт напруги, подібний до ліній висот на географічній контурній карті; на малюнку 8 показані візерунки навколо кругових та гострих тріщин напружених стояків. Можливо, достатньо просто спостерігати місця високої щільності бахроми, щоб відзначити наявність концентрацій напружень, які потім можуть бути усунені відповідними конструктивними модифікаціями (наприклад, закругленням кутів або переміщенням різких геометричних розривів з областей високого напруження). Якщо використовується біле, а не монохроматичне світло, спостерігаються яскраві лінії, а не темні бахроми, причому кожен колір є доповненням того кольору, який був вимирання відповідно до рівняння 5.2.4. Ці смуги постійного кольору називаються ізохроматикою.

Перетворення шаблонів бахроми в числові значення напруги зазвичай є простим, але нудним, оскільки бахроми пов'язані з різницею напружень,\(\sigma_1 - \sigma_2\) а не з одним напруженням. Однак на вільній межі компоненти напруги, нормальні до межі, повинні бути нульовими, що означає, що напруга, тангенціальна до межі, є основним напруженням і тому задається безпосередньо порядком бахроми там. Зведення фотопружних візерунків до числових значень зазвичай передбачає початок з цих вільних поверхонь, а потім поступово працювати у внутрішню частину тіла за допомогою графічної процедури.

Муар

Термін «муар» пишеться маленьким «м» і походить не від чийогось імені, а від назви шовкової тканини, на якій зображені візерунки світлих і темних смуг. Смуги такого роду також розвиваються шляхом накладення двох майже однакових решіток, таких як можна побачити при перегляді через два віконні екрани, злегка повернуті один від одного. Малюнок 9 демонструє, що бахроми розвиваються, якщо дві сітки мають різний інтервал, а також різну орієнтацію. Бахроми різко змінюються навіть для невеликих рухів або деформацій у решітках, і це візуальне посилення руху може бути використано для виявлення та кількісної оцінки деформації в зразку.

Малюнок 9: Муарові бахроми, розроблені різницею кроку лінії (а) та орієнтації лінії (b). (Професор Фу-Пен Чіанг, Сонячний Стоуні-Брук.)

Як просту ілюстрацію аналізу деформації муару, припустимо, що решітка вертикальних ліній інтервалу\(p\) (\ зразок» решітки) прикріплена до зразка і що це спостерігається, переглядаючи іншу\ еталонну» решітку того ж періоду, але не пов'язану зі зразком. Тепер дайте зразку піддаватися деформації, щоб решітка зразка розтягнулася до періоду\(p'\). Темна бахрома з'явиться, коли лінії з двох решіток накладаються, і це станеться\(N(p' - p) = p\), коли після\(N\) ліній на сітці зразка інкрементний проміжок (\(p' - p\)) накопичиться до однієї опорної відстані кроку\(p\). Відстань\(S\) між окантовками тоді

\[S = Np' = \dfrac{pp'}{p' - p}\]

Нормальна\(\epsilon_x\) деформація в горизонтальному напрямку тепер дається безпосередньо з інтервалу бахроми як

\[\epsilon_x = \dfrac{p' - p}{p} = \dfrac{p}{S}\]

Бахроми також розвиватимуться, якщо сітка зразка зазнає обертання щодо опорної сітки: якщо обертання невелике, то

\(\dfrac{p}{S} = \tan \theta \approx \theta\)

\(S = \dfrac{p}{\theta}\)

Цей кут також є деформацією зсуву\(\gamma_{xy}\), тому

\[\gamma_{xy} = \theta = \dfrac{p}{\theta}\]

Більш загально розгляньте інтерференційні смуги, які розвиваються між вертикальною опорною сіткою та довільно зміщеною сіткою зразків (спочатку вертикальною). Бахрома нульового порядку (\(N = 0\)) полягає в тому, що відповідно до положень, що мають нульове горизонтальне зміщення, бахрома першого порядку (\(N = 1\)) відповідає горизонтальним рухам рівно на один крок відстані і т.д. горизонтальне зміщення задається безпосередньо порядком бахроми як\(u = N_p\), з якого штам дається

\[\epsilon_x = \dfrac{\partial u}{\partial x} = p \dfrac{\partial N}{\partial x}\]

так напруга дається як нахил бахроми.

Аналогічно, муаровий малюнок, розроблений між двома спочатку горизонтальними сітками, що характеризуються бахромою,\(N' = 0, 1, 2, \cdots\) дає вертикальні деформації:

\[\epsilon _y = \dfrac{\partial v}{\partial y} = \dfrac{\partial (N'p)}{\partial y} = p \dfrac{\partial N'}{\partial y}\]

Штами зсуву знаходять зі схилів як\(u\) -поля, так і\(v\) -поля:

\[\gamma_{xy} = p(\dfrac{\partial N}{\partial y} + \dfrac{\partial N'}{\partial x})\]

На малюнку 10 показані бахроми, відповідні вертикальним зміщенням навколо круглого отвору в плиті, що піддається навантаженню в\(y\) -напрямку. Вертикальна\(\epsilon_y\) деформація пропорційна\(y\) -відстані між цими бахромами, кожна з яких є контуром постійного вертикального зміщення. Ця деформація найбільша по\(x\) -осі на периферії отвору, і найменша по\(y\) осі -на периферії отвору.

Малюнок 10: Муарові візерунки вертикальних зміщень бруса з отвором під чистим натягом. (Професор Фу-Пен Чіанг, Сонячний Стоуні-Брук.)

Вправа\(\PageIndex{1}\)

\(0^{\circ}\)/\(45^{\circ}\)/\(90^{\circ}\)триплеча тензометрична розетка, прикріплена до сталевого зразка, дає показання\(\epsilon_0 = 175 \mu\)\(\epsilon_{45} =150\mu\), і\(\epsilon_{90} = -120\mu\). Визначте основні напруги і орієнтацію головних площин в місці розташування калібру.

Вправа\(\PageIndex{2}\)

Повторіть попередню проблему, але з показаннями\(\epsilon_0 = 150 \mu, \epsilon_{45} = 200 \mu\) датчиків, і\(\epsilon_{90} = 125 \mu\).