5.3: Аналіз скінченних елементів

Вступ

Аналіз кінцевих елементів (ЗЕД) став звичним явищем в останні роки і зараз є основою багатомільярдної промисловості на рік. Чисельні рішення навіть дуже складних стресових задач тепер можна отримати регулярно за допомогою ЗЕД, і метод настільки важливий, що навіть вступні процедури механіки матеріалів - такі як ці модулі - повинні окреслити його основні особливості.

Незважаючи на велику силу ЗЕД, недоліки комп'ютерних рішень необхідно мати на увазі при використанні цього та подібних методів: вони не обов'язково виявляють, як на напруження впливають важливі змінні проблеми, такі як властивості матеріалів і геометричні особливості, а також помилки у вхідних даних можуть виробляти дико неправильні результати, які аналітик може не помітити. Мабуть, найважливішою функцією теоретичного моделювання є загострення інтуїції дизайнера; користувачі кодів кінцевих елементів повинні планувати свою стратегію в цьому напрямку, доповнюючи комп'ютерне моделювання якомога більшою кількістю закритої форми та експериментального аналізу.

Коди кінцевих елементів менш складні, ніж багато пакетів обробки текстів та електронних таблиць, знайдених на сучасних мікрокомп'ютерах. Проте, вони досить складні, що більшість користувачів не вважають ефективним програмування власного коду. Доступний ряд попередньо написаних комерційних кодів, що представляють широкий ціновий діапазон і сумісні з машинами від мікрокомп'ютерів до суперкомп'ютерів (C.A. Brebbia, ред., Finite Element Systems, A Handbook, Springer-Verlag, Берлін, 1982.). Однак користувачі зі спеціалізованими потребами не обов'язково повинні ухилятися від розробки коду, і можуть знайти джерела коду, доступні в таких текстах, як Zienkiewicz (O.C. Zienkiewicz та R.L. Taylor, Метод кінцевих елементів, McGraw-Hill Co., Лондон, 1989.), щоб бути корисною відправною точкою. Більшість кінцевих елементів програмного забезпечення написано на Fortran, але деякі нові коди, такі як фетр, знаходяться в C або інших більш сучасних мовах програмування.

На практиці кінцево-елементний аналіз зазвичай складається з трьох основних етапів:

1. Попередня обробка: Користувач будує модель деталі, що підлягає аналізу, в якій геометрія розділена на ряд дискретних субобластей, або «елементів», з'єднаних у дискретних точках, які називаються «вузлами». Деякі з цих вузлів матимуть фіксовані зсуви, а інші матимуть прописані навантаження. Ці моделі можуть бути надзвичайно трудомісткими для підготовки, і комерційні коди змагаються один з одним, щоб мати найбільш зручний графічний «препроцесор», щоб допомогти в цій досить нудній роботі. Деякі з цих препроцесорів можуть накладати сітку на попередньо існуючий файл CAD, так що аналіз кінцевих елементів може бути зроблено зручно як частина комп'ютеризованого процесу складання та проектування.

2. Аналіз: набір даних, підготовлений препроцесором, використовується як вхід до самого коду скінченних елементів, який будує та вирішує систему лінійних або нелінійних алгебраїчних рівнянь

\(K_{ij} u_j = f_i\)

де\(u\) і\(f\) є зміщення і зовнішньо прикладені сили в вузлових точках. Формування\(K\) матриці залежить від типу задачі, що атакується, і цей модуль окреслює підхід до аналізу напружень ферми та лінійних пружних напружень. Комерційні коди можуть мати дуже великі бібліотеки елементів, з елементами, відповідними широкому діапазону типів проблем. Однією з головних переваг ЗЕД є те, що багато типів проблем можна вирішити за допомогою одного коду, лише вказавши відповідні типи елементів з бібліотеки.

3. Постобробка: У попередні дні аналізу скінченних елементів користувач поривав через потоки чисел, згенерованих кодом, перераховуючи переміщення та напруження в дискретних положеннях у моделі. Таким чином легко пропустити важливі тенденції та гарячі точки, а сучасні коди використовують графічні дисплеї, щоб допомогти візуалізувати результати. Типовий постпроцесорний дисплей накладає кольорові контури, що представляють рівні напружень на моделі, показуючи зображення повного поля, подібне до фотоеластичних або муарових експериментальних результатів

Робота конкретного коду, як правило, детально описана в документації, що супроводжує програмне забезпечення, і постачальники більш дорогих кодів часто пропонують семінари або навчальні заняття, а також, щоб допомогти користувачам дізнатися тонкощі роботи коду. Одна проблема, яку користувачі можуть мати навіть після цього навчання, полягає в тому, що код, як правило, є «чорним ящиком», внутрішня робота якого не зрозуміла. У цьому модулі ми викладемо принципи, що лежать в основі більшості поточних кодів аналізу напружень кінцевих елементів, обмежуючи обговорення лінійним еластичним аналізом на даний момент. Розуміння цієї теорії допомагає розсіювати синдром чорного ящика, а також служить для узагальнення аналітичних основ механіки твердого тіла.

Матричний аналіз ферм

Ферми, з'єднані з штифтами, більш повно розглянуті в модулі 5, забезпечують хороший спосіб впровадження концепцій ЗЕД. Статичний аналіз ферм може бути проведений точно, а рівняння навіть складних ферм можуть бути зібрані в матричному вигляді, піддається числовому розв'язку. Такий підхід, який іноді називають «матричним аналізом», заклав основу раннього розвитку ЗЕД.

Матричний аналіз ферм працює шляхом розгляду жорсткості кожного кроквяного елемента по одному, а потім за допомогою цих жорсткостей визначити зусилля, які задаються в кроквяних елементах зміщеннями з'єднань, зазвичай званих «вузлами» в кінцевому елементному аналізі. Потім зазначивши, що сума сил, внесених кожним елементом до вузла, повинна дорівнювати силі, яка зовні застосовується до цього вузла, ми можемо зібрати послідовність лінійних алгебраїчних рівнянь, в яких вузлові зміщення є невідомими, а прикладені вузлові сили - відомі величини. Ці рівняння зручно записувати в матричному вигляді, що дає методу свою назву:

\(\begin{bmatrix} K_{11} & K_{12} & \cdots & K_{1n} \\ K_{21} & K_{22} & \cdots & K_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ K_{n1} & K_{n2} & \cdots & K_{nn} \end{bmatrix} \left \{ \begin{array} {c} u_1 \\ u_2 \\ \cdots \\ u_n \end{array} \right \} = \left \{ \begin{array} {c} f_1 \\ f_2 \\ \cdots \\ f_n \end{array} \right \}\)

Тут\(u_i\) і\(f_j\) вказують відхилення на i-му вузлі і силу на\(j^{th}\) вузлі (це насправді були б векторні величини, з підкомпонентами уздовж кожної координатної осі). Масив\(K_{ij}\) коефіцієнтів називається глобальною матрицею жорсткості, причому\(ij\) компонент фізично впливає\(j^{th}\) зміщення на\(i^{th}\) силу. Матричні рівняння можна скорочувати як

\[K_{ij} u_j = f_i \text{ or } Ku = f\]

використовуючи або індекси, або напівжирний шрифт для позначення векторних та матричних величин.
Або сила, що застосовується зовні, або зміщення відома на початку для кожного вузла, і неможливо вказати одночасно як довільне зміщення, так і силу на даному вузлі. Ці передбачені вузлові сили і зсуви є граничними умовами задачі. Завданням аналізу є визначення сил, які супроводжують нав'язані зсуви, і зміщення у вузлах, де застосовуються відомі зовнішні сили.

Матриця жорсткості для одного кроквяного елемента

В якості першого кроку в розробці набору матричних рівнянь, що описують кроквяні системи, нам потрібна залежність між силами і переміщеннями на кожному кінці окремого кроквяного елемента. Розглянемо такий елемент в\(x - y\) площині, як показано на малюнку 1, прикріплений до вузлів\(j\) пронумерованим\(i\) і нахиленим під кутом\(\theta\) від горизонталі.

Малюнок 1: Індивідуальний кроквяний елемент.

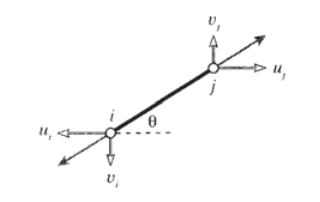
З огляду на вектор подовження, який\(\delta\) потрібно вирішити в напрямках уздовж і поперечно елементу, подовження в кроквяному елементі можна записати в терміні відмінностей зміщень його кінцевих точок:

де\(u\) і\(v\) горизонтальна і вертикальна складові прогинів відповідно. (Зсуви у вузлі,\(i\) намальованому на малюнку 1, є негативними.) Це відношення може бути записано в матричному вигляді як:

\(\delta = \begin{bmatrix} -c & -s & c & s \end{bmatrix} \left \{ \begin{array} {c} u_i \\ v_i \\ u_j \\ v_j \end{array} \right \}\)

Ось\(c = \cos \theta\) і\(s = \sin \theta\).

Осьова сила\(P\), яка супроводжує подовження,\(\delta\) задається законом Гука для лінійних пружних тіл як\(P = (AE/L) \delta\). Горизонтальні та вертикальні вузлові сили показані на малюнку 2; їх можна записати через загальну осьову силу як:

Малюнок 2: Складові вузлової сили.

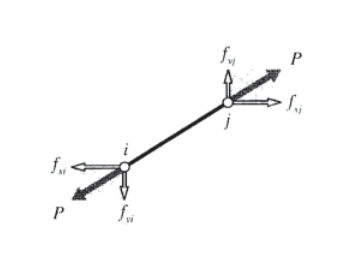
\(\left \{ \begin{array} {c} f_{xi} \\ f_{yi} \\ f_{xj} \\ f_{yj} \end{array} \right \} = \left \{ \begin{array} {c} -c \\ -s \\ c \\ s \end{array} \right \} P = \left \{ \begin{array} {c} -c \\ -s \\ c \\ s \end{array} \right \} \dfrac{AE}{L} \delta\)

\(= \left \{ \begin{array} {c} -c \\ -s \\ c \\ s \end{array} \right \} \dfrac{AE}{L} \begin{bmatrix} -c & -s & c & s \end{bmatrix} \left \{ \begin{array} {c} u_i \\ v_i \\ u_j \\ v_j \end{array} \right \}\)

Проведення множення матриці:

\[\left \{ \begin{array} {c} f_{xi} \\ f_{yi} \\ f_{xj} \\ f_{yj} \end{array} \right \} = \dfrac{AE}{L} \begin{bmatrix} c^2 & cs & -c^2 & -cs \\ cs & s^2 & -cs & -s^2 \\ -c^2 & -cs & c^2 & cs \\ -cs & -s^2 & cs & s^2 \end{bmatrix} \left \{ \begin{array} {c} u_i \\ v_i \\ u_j \\ v_j \end{array} \right \}\]

Величина в дужках, помножена на\(AE/L\), відома як «матриця жорсткості елемента»\(k_{ij}\). Кожен його термін має фізичне значення, представляючи собою внесок одного з переміщень в одну з сил. Глобальна система рівнянь формується шляхом об'єднання матриць жорсткості елементів з кожного кроквяного елемента по черзі, тому їх обчислення займає центральне місце в методі матричного структурного аналізу. Принципова відмінність методу матричної ферми від загального методу скінченних елементів полягає в тому, як формуються матриці жорсткості елементів; більшість інших комп'ютерних операцій однакові.

Збірка кількох внесків елементів

Малюнок 3: Внесок елемента в загальну вузлову силу.

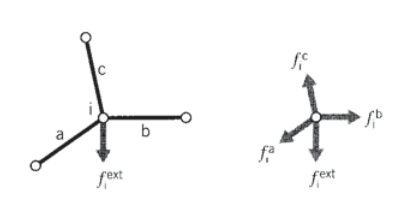
Наступним кроком слід розглянути збірку багатьох кроквяних елементів, з'єднаних штифтовими з'єднаннями. Кожен елемент, що зустрічається на стику, або вузол, сприятиме силі там, як це продиктовано зміщеннями обох вузлів цього елемента (див. Рис. Для підтримки статичної рівноваги всі вклади сили елемента\(f_{i}^{elem}\) в даному вузлі повинні сумувати силу\(f_i^{ext}\), яка зовнішньо прикладена до цього вузла:

\(f_i^{ext} = \sum_{elem} f_i^{elem} = (\sum_{elem} k_{ij}^{elem} u_j) = (\sum_{elem} k_{ij}^{elem}) u_j = K_{ij} u_j\)

Кожен елемент матриці жорсткості\(k_{ij}^{elem}\) додається до відповідного розташування загальної, або «глобальної» матриці жорсткості\(K_{ij}\), яка пов'язує всі зміщення і зусилля ферми. Цей процес називається «збірка». Індексні номери в зазначеному вище співвідношенні повинні бути «глобальними» номерами, присвоєними кроквяної конструкції в цілому. Однак, як правило, зручно обчислювати окремі матриці жорсткості елементів за локальною схемою, а потім змусити комп'ютер перетворювати в глобальні числа при складанні окремих матриць.

Приклад\(\PageIndex{1}\)

Процес складання лежить в основі методу кінцевих елементів, і варто зробити простий випадок вручну, щоб побачити, як він насправді працює. Розглянемо двоелементну кроквяну задачу на рис. 4, при цьому вузлам присвоюються довільні «глобальні» числа від 1 до 3. Оскільки кожен вузол взагалі може рухатися в двох напрямках, в задачі є\(3 \times 2 = 6\) загальні ступені свободи. Глобальна матриця жорсткості буде\(6 \times 6\) масивом, що стосується шести переміщень з шістьма зовнішніми прикладними силами. Тільки одне з переміщень в даному випадку невідомо, так як всі, крім вертикального зміщення вузла 2 (ступінь свободи № 4) обмежені нулем. На малюнку 4 показаний працездатний перелік глобальних чисел, а також «локальних» чисел для кожного окремого елемента.

Малюнок 4: Глобальна і локальна нумерація для двоелементної ферми.

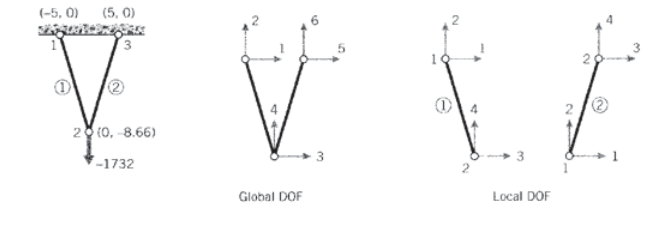
Використовуючи локальні числа, матрицю жорсткості\(4 \times 4\) елемента кожного з двох елементів можна оцінити за рівнянням 5.3.2. Кут нахилу розраховується з вузлових координат як

Отримана матриця для елемента 1 дорівнює:

\(k^{(1)} = \begin{bmatrix} 25.00 & -43.30 & -25.00 & 43.30 \\ -43.30 & 75.00 & 43.30 & -75.00 \\ -25.00 & 43.30 & 25.00 & -43.30 \\ 43.30 & -75.00 & -43.30 & 75.00 \end{bmatrix} \times 10^3\)

і для елемента 2:

\(k^{(2)} = \begin{bmatrix} 25.00 & 43.30 & -25.00 & -43.30 \\ 43.30 & 75.00 & -43.30 & -75.00 \\ -25.00 & -43.30 & 25.00 & 43.30 \\ -43.30 & -75.00 & 43.30 & 75.00 \end{bmatrix} \times 10^3\)

(Важливо одиниці бути послідовними; тут довжини в дюймах, сили в фунтах, і модулі в фунтах на квадратний дюйм. Модуль обох елементів\(E = 10\) Mpsi і обидва мають площу\(A = 0.1 in^2\).) Ці матриці мають рядки і стовпці, пронумеровані від 1 до 4, що відповідають локальним ступеням свободи елемента.

Однак кожна з місцевих ступенів свободи може бути підібрана до однієї з глобальних ступенів загальної проблеми. Оглядаючи рисунок 4, ми можемо сформувати наступну таблицю, яка відображає локальні та глобальні числа:

місцевий	глобальний, елемент 1	глобальний, елемент 2
1	1	3
2	2	4
3	3	5
4	4	6

Використовуючи цю таблицю, ми бачимо, наприклад, що друга ступінь свободи для елемента 2 є четвертою ступенем свободи в глобальній системі нумерації, а третя локальна ступінь свободи відповідає п'ятій глобальній мірі свободи. Звідси значення в другому рядку і третьому стовпці матриці жорсткості елемента 2, позначені\(k_{23}^{(2)}\), слід додати в положення в четвертому рядку і п'ятому стовпці\(6 \times 6\) глобальної матриці жорсткості. Ми пишемо це як

\(k_{23}^{(2)} \to K_{4,5}\)

Кожна з шістнадцяти позицій в матриці жорсткості кожного з двох елементів повинна бути додана в глобальну матрицю відповідно до відображення, заданого таблицею. Це дає результат

\(K = \begin{bmatrix} k_{11}^{(1)} & k_{12}^{(1)} & k_{13}^{(1)} & k_{14}^{(1)} & 0 & 0 \\ k_{21}^{(1)} & k_{22}^{(1)} & k_{23}^{(1)} & k_{24}^{(1)} & 0 & 0 \\ k_{31}^{(1)} & k_{32}^{(1)} & k_{33}^{(1)} + k_{11}^{(2)} & k_{34}^{(1)} + k_{12}^{(2)} & k_{13}^{(2)} & k_{14}^{(2)} \\ k_{41}^{(1)} & k_{42}^{(1)} & k_{43}^{(1)} + k_{21}^{(2)} & k_{44}^{(1)} + k_{22}^{(2)} & k_{23}^{(2)} & k_{24}^{(2)} \\ 0 & 0 & k_{31}^{(2)} & k_{32}^{(2)} & k_{33}^{(2)} & k_{34}^{(2)} \\ 0 & 0 & k_{41}^{(2)} & k_{42}^{(2)} & k_{43}^{(2)} & k_{44}^{(2)} \end{bmatrix}\)

Ця матриця попередньо множить вектор вузлових переміщень згідно Рівняння 5.3.1 для отримання вектора зовнішніх прикладених вузлових сил. Повні системні рівняння, з урахуванням відомих сил і переміщень, потім

Зверніть увагу, що або сила, або зміщення для кожного ступеня свободи відомі, при цьому супутні зміщення або сила невідомі. Тут невідомий лише один з переміщень (\(u_4\)), але в більшості проблем невідомі переміщення значно перевершують невідомі сили. Зауважте також, що тільки ті елементи, які фізично пов'язані з заданим вузлом, можуть сприяти зусиллям цього вузла. У більшості випадків це призводить до глобальної матриці жорсткості, яка містить багато нулів, відповідних вузловим парам, які не охоплюються елементом. Ефективні комп'ютерні реалізації дозволять скористатися розрідженістю матриці для економії пам'яті та скорочення часу виконання.

У великих задачах матричні рівняння вирішуються для невідомих переміщень і сил за допомогою гаусового скорочення або інших методів. У цій двоелементній задачі рішення для єдиного невідомого зміщення можна записати майже з огляду. Перемноживши четвертий ряд системи, ми маємо

\(0 + 0 + 0 + 150 \times 10^3 u_4 + 0 + 0 = -1732\)

\(u_4 = -1732/150 \times 10^3 = -0.01155 in\)

Тепер будь-яку з невідомих сил можна отримати безпосередньо. Наприклад, множення першого рядка дає

\(0 + 0 + 0 + (43.4) (-0.0115) \times 10^3 + 0 + 0 = f_1\)

Негативний знак тут вказує на горизонтальну силу на глобальному вузлі #1 знаходиться вліво, протилежному напрямку, передбаченому на малюнку 4.

Процес циклічності через кожен елемент для формування матриці жорсткості елемента, складання матриці елемента в правильні позиції в глобальній матриці, рішення рівнянь для переміщень, а потім зворотне множення для обчислення сил, і друк результатів може бути автоматизований, щоб зробити дуже універсальний комп'ютерний код.

Більшого масштабу ферми (та інших) кінцевих елементів аналіз найкраще проводити за допомогою спеціального комп'ютерного коду, а відмінний для вивчення методу доступний з Інтернету за адресою http://felt.sourceforge.net/. Цей код, названий фетром, був автором Джейсона Гобата та Даррена Аткінсона для освітнього використання, і включає в себе ряд нових функцій для сприяння зручності користувачів. Повна інформація, що описує цей код, а також джерело мови C і ряд пробних запусків і допоміжних модулів коду доступна на їх веб-сторінках. Якщо у вас є доступ до робочих станцій X-window, також доступна графічна оболонка з назвою velvet.

Приклад\(\PageIndex{2}\)

Малюнок 5: Шестиелементна ферма, розроблена в графічному інтерфейсі FEA оксамитовий/повстяний.

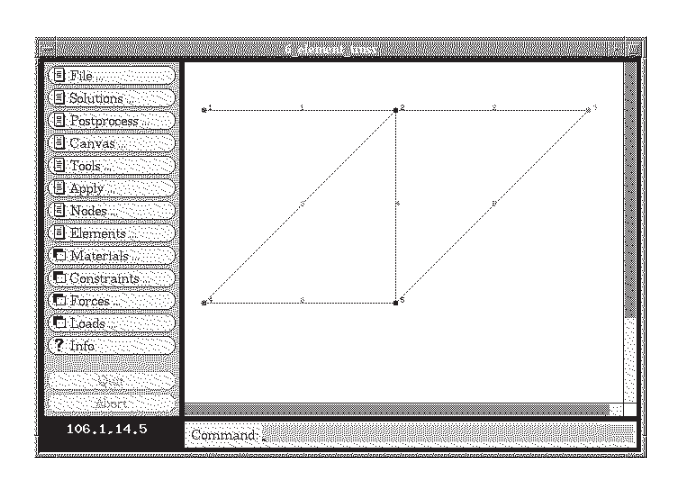
Щоб проілюструвати, як цей код працює для дещо більшої проблеми, розглянемо шестиелементну ферму малюнка 5, яка була проаналізована в Модулі 5 як спільним підходом до аналізу вільного тіла, так і методом Кастільяно.

Вхідний набір даних, який може бути написаний вручну або розроблений графічно в оксамиті, використовує методи синтаксичного аналізу, щоб спростити те, що може бути дуже нудним і схильним до помилок крок в аналізі скінченних елементів. Набір даних для цієї 6-елементної ферми:

problem description
nodes=5 elements=6
nodes
1 x=0 y=100 z=0 constraint=pin
2 x=100 y=100 z=0 constraint=planar 3 x=200 y=100 z=0 force=P
4 x=0 y=0 z=0 constraint=pin
5 x=100 y=0 z=0 constraint=planar 
truss elements
1  nodes=[1,2]
2  nodes=[2,3]
3  nodes=[4,2]
4  nodes=[2,5]
5  nodes=[5,3]
6  nodes=[4,5]

material=steel
material properties steel E=3e+07 A=0.5

distributed loads

constraints
free Tx=u Ty=u Tz=u Rx=u Ry=u Rz=u 
pin Tx=c Ty=c Tz=c Rx=u Ry=u Rz=u 
planar Tx=u Ty=u Tz=c Rx=u Ry=u Rz=u

forces
P Fy=-1000

end 

Сенс цих рядків повинен бути досить очевидним при огляді, хоча для отримання більш докладної інформації слід звернутися до повстяної документації. Вихід, вироблений фетром для цих даних, такий:

** **

вузлові зсуви

Вузол #	ДОЦ 1	ДОЦ 2	ДОЦ 3	ДОЦ 4	ДОЦ 5	ДОЦ 6
1	0	0	0	0	0	0
2	0.013333	-0.03219	0	0	0	0
3	0,02	-0.084379	0	0	0	0
4	0	0	0	0	0	0
5	-0.0066667	-0.038856	0	0	0	0

Напруження елементів

1:	4000
2:	2000
3:	-2828.4
4:	2000
5:	-2828.4
6:	-2000

Сили реакції

Вузол #	ДОЦ	Сила реакції
1	Tx	-2000
1	Тай	0
1	Tz	0
2	Tz	0
3	Tz	0
4	Tx	2000
4	Тай	1000
4	Tz	0
5	Tz	0

Резюме використання матеріалів

Матеріал: сталь
Кількість: 6
Довжина: 682.8427
Маса: 0.0000

Загальна маса: 0,0000

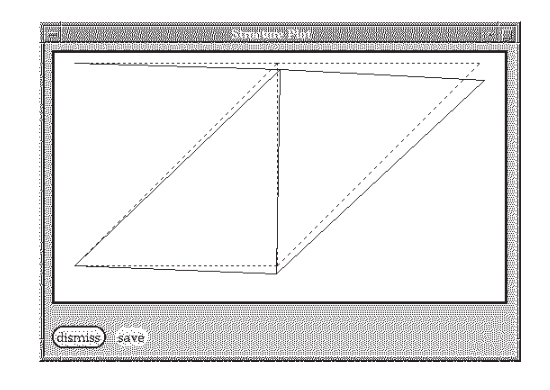
Вертикальне зміщення вузла 3 (значення DOF 2) становить -0,0844, таке ж значення, отримане методами замкнутої форми Модуля 5. На малюнку 6 показаний оксамитовий графічний вихід для прогинів ферми (значно збільшений).

Малюнок 6:6-елементна ферма в початковій і деформованій формі.

Загальний аналіз стресу

Матриця жорсткості елемента може бути сформована саме для елементів ферми, але це не стосується загальних ситуацій аналізу напружень. Співвідношення між вузловими силами і переміщеннями заздалегідь не відомо для загальних двох- або тривимірних задач аналізу напружень, і для запису матриці жорсткості елемента необхідно використовувати приблизне співвідношення.

У звичайній «формулюванні зміщення» методу скінченних елементів керуючі рівняння поєднуються таким чином, щоб мати лише зсуви, що з'являються як невідомі; це можна зробити за допомогою конституційних рівнянь Хукіана для заміни напружень у рівняннях рівноваги деформаціями, а потім використовуючи кінематичні рівняння для заміни деформацій на зсуви. Це дає

\[L^T \sigma = L^T D_{\epsilon} = L^T DLu = 0\]

Звичайно, часто неможливо розв'язати ці рівняння в замкнутому вигляді для нерегулярних зв'язкових умов, що зустрічаються в практичних задачах. Однак рівняння піддаються дискретизації та розв'язку за допомогою числових методів, таких як скінченні відмінності або скінченні елементи.

Методи скінченних елементів є однією з декількох наближених числових методів, доступних для розв'язання інженерних крайових задач. Проблеми механіки матеріалів часто призводять до рівнянь такого типу, а методи скінченних елементів мають ряд переваг при поводженні з ними. Метод особливо добре підходить для проблем з нерегулярною геометрією та граничними умовами, і він може бути реалізований в загальних комп'ютерних кодах, які можуть бути використані для багатьох різних завдань.

Для отримання числового розв'язку задачі аналізу напружень постулюємо функцію\(\tilde{u} (x, y)\) як наближення до\(u\):

\[\tilde{u} (x, y) \approx u (x, y)\]

Багато різних форм можуть бути прийняті для наближення\(\tilde{u}\). Метод скінченних елементів дискретизує область розв'язку на збірку субрегіонів, або «елементів», кожен з яких має свої апроксимуючі функції. Зокрема, наближення для переміщення\(\tilde{u} (x, y)\) всередині елемента записується як комбінація (поки невідомих) переміщень у вузлах, що належать цьому елементу:

\[\tilde{u} (x, y) = N_j (x, y) u_j\]

Тут індекс\(j\) коливається над вузлами елемента,\(u_j\) є вузловими зміщеннями та «функціями інтерполяції».\(N_j\) Ці функції інтерполяції зазвичай є простими поліномами (як правило, лінійними, квадратичними або іноді кубічними поліномами), які вибираються для того, щоб стати одиницею у вузлі\(j\) та нулем у інших вузлах елементів. Функції інтерполяції можуть бути оцінені в будь-якому положенні всередині елемента за допомогою стандартних підпрограм, тому наближене зміщення в будь-якому положенні всередині елемента можна отримати через вузлові зсуви безпосередньо з Рівняння 5.3.5.

Малюнок 7: Інтерполяція в одному вимірі.

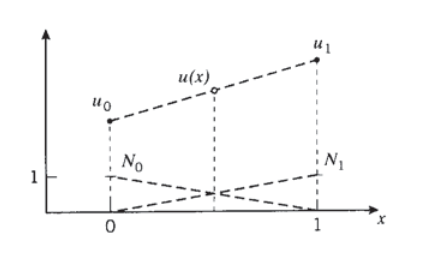
Концепція інтерполяції може бути проілюстрована, запитуючи, як ми можемо вгадати значення функції\(u(x)\) в довільній точці,\(x\) розташованій між двома вузлами в\(x = 0\) і\(x = 1\), припускаючи, що ми знаємо якось вузлові значення\(u(0)\) і u (1). Можна припустити, що як розумне наближення\(u(x)\) просто лінійно змінюється між цими двома значеннями, як показано на малюнку 7, і написати

Тут\(N_0\) і\(N_1\) - лінійні функції інтерполяції для цього одновимірного наближення. Коди кінцевих елементів мають підпрограми, які розширюють цю концепцію інтерполяції на два та три виміри.

Наближення для деформації і напруги випливають безпосередньо з переміщень:

\[\tilde{\epsilon} L\tilde{u} = LN_ju_j \equiv B_j u_j\]

\[\tilde{\sigma} D \tilde{\epsilon} = DB_j u_j\]

де\(B_j(x, y) = LN_j (x, y)\) - масив похідних функцій інтерполяції:

\[B_j = \begin{bmatrix} N_{j,x} & 0 \\ 0 & N_{j, y} \\ N_{j, y} & N_{j, x} \end{bmatrix}\]

Аргумент «віртуальної роботи» тепер може бути викликаний, щоб пов'язати вузлове зміщення,\(u_j\) що з'являється у вузлі\(j\), з силами, застосованими зовні на вузлі\(i\): якщо невелике, або «віртуальне,» зміщення\(\delta u_i\) накладається на вузол\(i\), збільшення енергії деформації в\(\delta U\) межах елемент, підключений до цього вузла, задається:

\[\delta U = \int_V \delta \epsilon^T \sigma dV\]

де\(V\) - обсяг елемента. Використовуючи наближену деформацію, отриману від інтерпольованих переміщень,\(\delta \tilde{\epsilon} = B_i \delta u_i\) наведено наближене віртуальне збільшення деформації, спричинене віртуальним вузловим зміщенням. Використовуючи рівняння 5.3.7 та ідентичність матриці\((AB)^T = B^T A^T\), ми маємо:

\[\delta U = \delta u_i^T \int_V B_i^T DB_j dV u_j\]

(Вузлові зміщення\(\delta u_i^T\) і не\(u_j\) є функціями\(x\) і\(y\), і тому можуть бути приведені зсередини інтеграла.) Збільшення енергії деформації\(\delta U\) повинно дорівнювати роботі, яку виконують вузлові сили; це:

\[\delta W = \delta u_i^T f_i\]

Прирівнюючи Eqns. 5.3.10 і 5.3.11 і скасовуючи загальний коефіцієнт\(\delta u_i^T\), ми маємо

\[[\int_V B_i^T DB_j dV] u_j = f_i\]

Це того, що має знежирену форму\(k_{ij} u_j = f_i\), де\(k_{ij} = \int_V B_i^T DB_j dV\) знаходиться жорсткість елемента.

Нарешті, інтеграл у рівнянні 12 повинен бути замінений числовим еквівалентом, прийнятним для комп'ютера. Чисельне інтегрування Гаусса-Лежандра зазвичай використовується в кодах скінченних елементів для цієї мети, оскільки ця техніка забезпечує високе відношення точності до обчислювальних зусиль. Коротко зазначено, інтеграція полягає в оцінці інтеграції в оптимально обраних точках інтеграції всередині елемента та формування зваженого підсумовування цілих значень у цих точках. У разі інтеграції над двовимірними елементними областями це можна записати:

\[\int_A f(x, y) dA \approx \sum_l f(x_l, y_l) w_l\]

Розташування точок відбору проб\(x_l,y_l\) і пов'язаних з ними ваг wl забезпечуються стандартними підпрограмами. У більшості сучасних кодів ці процедури відображають елемент у зручну форму, визначають точки інтеграції та ваги в перетвореному координатному кадрі, а потім відображають результати назад до вихідного кадру. Функції Nj, використані раніше для інтерполяції, також можуть бути використані для відображення, досягаючи значної економії в кодуванні. Це дає те, що відомо як «чисельно інтегровані ізопараметричні елементи», і вони є основою галузі кінцевих елементів.

Рівняння 5.3.12, з інтегралом, заміненим числовими інтеграціями виду в Рівнянні 5.3.13, є кінцевим елементом аналога Рівняння 5.3.3, диференціального керуючого рівняння. Комп'ютер буде проводити аналіз, циклічно над кожним елементом, і всередині кожного елемента циклів по окремих точках інтеграції. У кожній точці інтеграції компоненти матриці жорсткості елемента\(k_{ij}\) обчислюються відповідно до рівняння 5.3.12 і додаються до відповідних положень\(K_{ij}\) глобальної матриці жорсткості, як це було зроблено на етапі складання матричного методу ферми, описаного в попередньому розділі. Можна оцінити, що велика частина обчислень бере участь саме в формуванні термінів матриці жорсткості, і що метод скінченних елементів ніколи не міг бути розроблений без зручного і недорогого доступу до комп'ютера.

Напруження навколо круглого отвору

Розглянуто задачу одноосно навантаженої пластини, що містить круглий отвір у попередніх модулі, включаючи теоретичний розв'язок Кірша (модуль 16) та експериментальні визначення за допомогою фотопружного та муарового методів (модуль 17). Ця проблема має практичне значення - наприклад, ми відзначили небезпечну концентрацію напружень, яка з'являється поблизу отворів для заклепок - і вона також є досить вимогливою як в теоретичному, так і в числовому аналізі. Оскільки напруження різко зростають біля отвору, там повинна бути доопрацьована сітка кінцевих елементів, щоб отримати прийнятні результати.

Малюнок 8: Сітка для проблеми з круговим отвором.

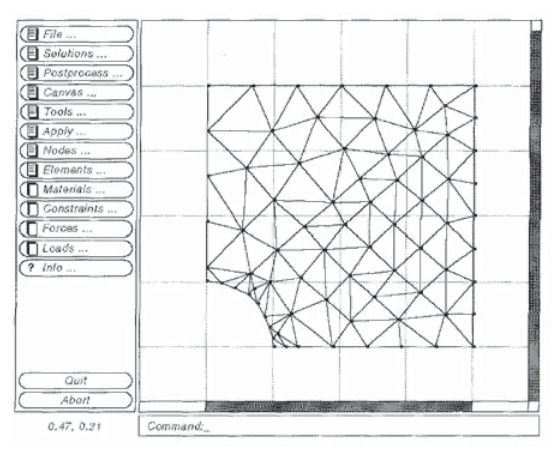
На малюнку 8 показана сітка з тривузлових трикутних елементів, розроблена фетрово-оксамитовим графічним пакетом ЗЕД, яка може бути використана для наближення переміщень і напружень навколо одноосно навантаженої пластини, що містить круглий отвір. Оскільки як теоретичні, так і експериментальні результати для цього поля напружень доступні, як зазначено вище, проблема кругового отвору є гарною для ознайомлення з операцією коду.

Користувач повинен скористатися симетрією, щоб зменшити розмір проблеми, коли це можливо, і в цьому випадку потрібно з'єднати лише один квадрант проблеми. Центр отвору тримається фіксованим, тому симетрія вимагає, щоб вузли по лівому краю могли рухатися вертикально, але не горизонтально. Аналогічно вузли вздовж нижнього краю обмежуються вертикально, але залишаються вільними для горизонтального переміщення. Навантаження прикладають до вузлів по верхньому краю, причому кожне навантаження є результатом напруги далекого поля, що діє по половині кордонів елемента між заданим вузлом і його сусідами. (Напруга далекого поля приймається як єдність.) Частини вхідного набору даних повсті для цієї проблеми:

problem description
nodes=76 elements=116
nodes
1  x=1 y=-0 z=0 constraint=slide_x
2  x=1.19644 y=-0 z=0
3  x=0.984562 y=0.167939 z=0 constraint=free
4  x=0.940634 y=0.335841 z=0
5  x=1.07888 y=0.235833 z=0
.
.
.
72  x=3.99602 y=3.01892 z=0
73  x=3.99602 y=3.51942 z=0
74  x=3.33267 y=4 z=0
75  x=3.57706 y=3.65664 z=0
76 x=4 y=4 z=0
CSTPlaneStress elements
1  nodes=[13,12,23]
2  nodes=[67,58,55]
6  nodes=[50,41,40]
.
.
.
7  nodes=[68,67,69]
8  nodes=[68,58,67]
9  nodes=[57,58,68]
10 nodes=[57,51,58]
11  nodes=[52,51,57]
12  nodes=[37,39,52]
13 nodes=[39,51,52]
.
.
.
116 nodes=[2,3,1]

material properties
steel E=2.05e+11 nu=0.33 t=1

distributed loads
load_case_1 color=red direction=GlobalY values=(1,1) (3,1)
constraints
free Tx=u Ty=u Tz=u Rx=u Ry=u Rz=u
slide_x color=red Tx=u Ty=c Tz=c Rx=u Ry=u Rz=u 
slide_y color=red Tx=c Ty=u Tz=c Rx=u Ry=u Rz=u

end 

\(y\)-зсуви та вертикальні напруги σy контуруються на малюнку 9 (a) та (b) відповідно; їх слід порівнювати з фотоеластичним та муаровим аналізами, наведеними в модулі 17, рис. 8 та 10 (а). Напруга в точці інтеграції, найближчій до осі х в отворі\(\sigma_{y, \max} = 3.26\), обчислюється на 9% більше теоретичного значення 3,00. При малюванні контурів малюнка 9b постпроцесор екстраполював напруги на вузли, підганяючи площину найменших квадратів через напруження у всіх чотирьох точках інтеграції всередині елемента. Це дає ще більш високе значення коефіцієнта концентрації напружень, 3.593. Користувач повинен знати, що графічні постпроцесори згладжують результати, які самі по собі є лише наближеннями, тому числова неточність є реальною можливістю. Уточнення сітки, особливо поблизу області найвищого градієнта напруги на меридіані отвору, зменшить цю похибку.

Малюнок 9: Вертикальні зміщення (a) та напруження (b), обчислені для сітки на малюнку 8.

Вправа\(\PageIndex{1}\)

(a) - (h) Використовуйте ЗЕД для визначення сили в кожному елементі ферм, намальованих нижче.

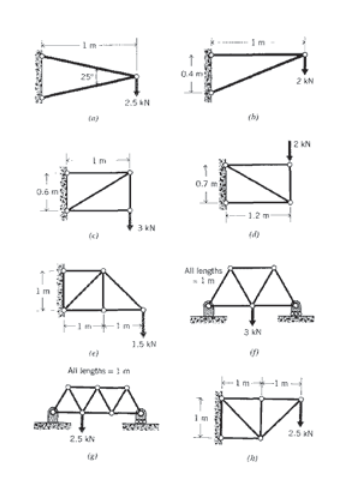
Вправа\(\PageIndex{2}\)

(a) — (c) Випишіть глобальні матриці жорсткості для ферм, перелічених нижче, та вирішіть для невідомих сил та переміщень. Для кожного елемента припускаємо\(E = 30\) Mpsi і\(A = 0.1 in^2\).

Вправа\(\PageIndex{3}\)

Отримати плосконапружений скінченно-елементний розчин для консольної балки з одним навантаженням на вільному кінці. Використовуйте довільно підібрані (але розумні) розміри і властивості матеріалу. Побудуйте напруження\(\sigma_x\) і\(\tau_{xy}\) як функції\(y\) на довільній станції вздовж прольоту; також побудуйте напруження, задані елементарною теорією вигину балки (cf модуль 13) і оцініть величину числової похибки.

Вправа\(\PageIndex{4}\)

Повторіть попередню задачу, але з симетрично навантаженою балкою в триточковому вигині.

Вправа\(\PageIndex{5}\)

Використовуйте осесимметричні елементи для отримання кінцевого елементного рішення для радіального напруження в товстостінній посудині під тиском (з використанням довільної геометрії та параметрів матеріалу). Порівняти результати з теоретичним розв'язком (cf Prob. 2 у модулі 16).