5.1: Рішення закритої форми
- Page ID
- 30714
Вступ
Під час більшої частини свого історичного розвитку наука про механіку матеріалів спиралася головним чином на математичних теоретиків замкнутої форми (не обчислювальних). Значна частина їхньої роботи являє собою математичну інтуїцію і майстерність дуже високого порядку, що викликає навіть для передових дослідників сьогоднішнього дня. Ця теорія викладається насамперед у випускниках предметів, але тут викладено як для надання деякої довідки, яка буде корисна в Модулі про перелом, так і як попередній вступ до цих більш просунутих предметів.
Керуючі рівняння
Раніше ми показали (див. Модуль 9), як просторові градієнти шести напружень Коші пов'язані трьома рівняннями рівноваги, які можна записати в псевдовекторній формі як
\[L^T \sigma = 0\]
Вони доповнені шістьма складовими рівняннями, які можуть бути записані для лінійних пружних матеріалів як (див. Модуль 11)
\[\sigma = D \epsilon\]
і шість рівнянь кінематичного або деформаційного зміщення (модуль 8)
\[\sigma = Lu\]
Ці п'ятнадцять рівнянь повинні задовольнятися п'ятнадцятьма незалежними функціями (три зміщення\(u\), шість деформацій\(\epsilon\) і шість напружень\(\sigma\)). Ці функції також повинні задовольняти граничним умовам по зміщенню.
\[u = \hat{u} \text{ on } \Gamma_u\]
де\(\Gamma_u\) - ділянка кордону, на якій\(u = \hat{u}\) прописуються зсуви. Залишок кордону повинен мати прописані тяги\(T = \hat{T}\), на яких напруги повинні задовольняти відношення Коші:
\[\sigma \hat{n} = \hat{T} \text{ on } \Gamma_T\]
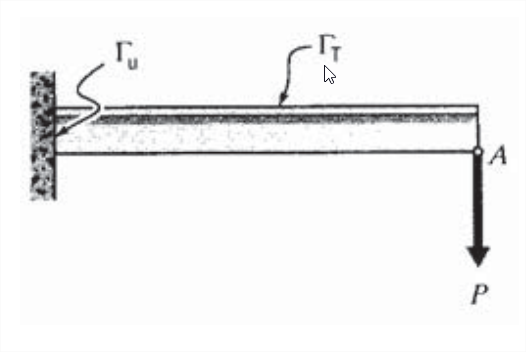
У знайомій консольної балці, показаної на малюнку\(\PageIndex{1}\), область балки у стіни становить\(\Gamma_u\), задавши (нуль) зміщення і ухил. Всі інші точки на кордоні балки складають\(\Gamma_T\), з навантаженням\(P\) в точці навантаження\(A\) і заданим нульовим навантаженням в іншому місці.
З такими структурами, як балка, які мають прості геометрії, рішення можуть бути отримані прямим методом, який ми використовували в попередніх модулів: пишеться вираз для переміщень, з якого можна отримати деформації та напруження, а потім врівноважуватися проти зовнішніх прикладених навантажень. (Вправа\(\PageIndex{2}\) дає ще один приклад цього процесу.) У ситуаціях, які не мають такої геометричної простоти, аналітик повинен здійснити математичне рішення, шукаючи функції напруги, деформації та переміщення, які задовольняють як керуючим рівнянням, так і граничним умовам.
В даний час практичні завдання, швидше за все, будуть вирішуватися обчислювальним наближенням, але майже завжди краще отримати рішення закритої форми, якщо це взагалі можливо. Математичний результат покаже функціональну важливість різних параметрів, таких як умови навантаження або властивості матеріалу, таким чином, числове рішення не може, і тому є більш корисним для керівництва проектними рішеннями. З цієї причини проектувальник завжди повинен починати аналіз несучих конструкцій з пошуку закритих рішень даної, або подібної, проблеми. Доступно кілька збірників таких рішень, корисним прикладом є книга Roark (W.C. Young, Формули Roark для стресу і деформації, Макгроу-Хілл, Нью-Йорк, 1989.).
Однак завжди існує небезпека виконувати такого роду «посібник з інженерії» наосліп, і цей розділ покликаний частково проілюструвати математичні концепції, які лежать в основі багатьох з цих опублікованих рішень. Ймовірно, правда, що більшість завдань, які можуть бути вирішені математично, вже завершені, це класичні завдання прикладної механіки, і вони часто вимагають досить високого рівня математичної витонченості. Класичний текст Тимошенко і Гуді (С.Тимошенко і Ю.Н. Гудье, Теорія пружності, Макгроу-Хілл, Нью-Йорк, 1951 р.) є відмінним джерелом для подальшого читання в цій області.
Функція стресу Ейрі
Розширення кінематичних рівнянь або рівнянь деформаційного переміщення (Рівняння 5.1.3) в двох вимірах дає знайомі форми:
\[\begin{array} {rcl} {\epsilon_x} & = & {\dfrac{\partial u}{\partial x}} \\ {\epsilon_y} & = & {\dfrac{\partial v}{\partial y}} \\ {\gamma_{xy}} & = & {\dfrac{\partial v}{\partial x} + \dfrac{\partial u}{\partial y}} \end{array}\]
Оскільки три штами\((\epsilon_x, \epsilon_y, \gamma_{xy})\) записуються лише двома зміщеннями\((u,v)\), вони не можуть бути визначені довільно; між трьома деформаціями має існувати зв'язок. Якщо\(\epsilon_x\) диференціюється\(dx, \epsilon_y\) двічі на два рази\(dy\), і\(\gamma_{xy}\) до\(dx\) і тоді\(dy\) ми маємо безпосередньо
\[\dfrac{\partial^2 \epsilon_x}{\partial y^2} + \dfrac{\partial^2 \epsilon_y}{\partial x^2} = \dfrac{\partial^2 \gamma_{xy}}{\partial x \partial y}\]
Для того, щоб переміщення були настільки диференційованими, вони повинні бути безперервними функціями, що означає фізично, що тіло повинно деформуватися сумісним чином, тобто без розвитку тріщин або перекриттів. З цієї причини Рівняння 5.1.7 називають рівнянням сумісності для деформацій, оскільки безперервність тіла гарантується, якщо деформації задовольняють його.
Рівняння сумісності можна записати через напруження, а не деформації, згадуючи складові рівняння для пружного плоского напруження:
\[\begin{array} {c} {\epsilon_x = \dfrac{1}{E} (\sigma_x - v \sigma_y)} \\ {\epsilon_y = \dfrac{1}{E} (\sigma_y - v \sigma_x)} \\ {\gamma_{xy} = \dfrac{1}{G} \tau_{xy} = \dfrac{2(1 + v)}{E} \tau_{xy}} \end{array}\]
Заміна їх у рівнянні 5.1.7 дає
\[\dfrac{\partial^2}{\partial y^2} (\sigma_x - v \sigma_y) + \dfrac{\partial^2}{\partial x^2} (\sigma_y - v \sigma_x) = 2 (1 + v) \dfrac{\partial^2 \tau_{xy}}{\partial x \partial y}\]
Стреси, що задовольняють це відношення, гарантують сумісність деформації.
Напруги також повинні задовольняти рівняння рівноваги, які в двох вимірах можуть бути записані
\(\dfrac{\partial \sigma_x}{\partial x} + \dfrac{\partial \tau_{xy}}{\partial y} = 0\)
\[\dfrac{\partial \tau_{xy}}{\partial x} + \dfrac{\partial \sigma_y}{\partial y} = 0\]
Як засіб спрощення пошуку функцій, похідні яких підпорядковуються цим правилам, Г.Б. Ейрі (1801—1892) визначив функцію напружень,\(\phi\) з якої напруження можна отримати диференціацією:
\[\begin{array} {rcl} {\sigma_x} & = & {\dfrac{\partial^2 \phi}{\partial y^2}} \\ {\sigma_y} & = & {\dfrac{\partial^2 \phi}{\partial x^2}} \\ {\tau_{xy}} & = & {-\dfrac{\partial^2 \phi}{\partial x \partial y}} \end{array}\]
Пряме заміщення покаже, що напруги, отримані в результаті цієї процедури, автоматично задовольнять рівняння рівноваги. Цей маневр по суті обмежений двовимірними задачами, але з цією умовою він забезпечує значне спрощення в пошуку дійсних функцій для напружень.
Тепер підставляючи їх в рівняння 5.1.9, ми маємо
\[\dfrac{\partial^4 \phi}{\partial x^4} + 2\dfrac{\partial^4 \phi}{\partial x^2 \partial y^2} + \dfrac{\partial^4 \phi}{\partial y^4} \equiv \nabla^2(\nabla^2 \phi) \equiv \nabla^4 \phi = 0\]
\(\phi (x, y)\)Будь-яка функція, яка задовольняє це відношення, задовольнить регулюючі відносини рівноваги, геометричної сумісності та лінійної пружності. Звичайно, можна записати багато функцій, які задовольняють рівнянню сумісності; наприклад, налаштування\(\phi = 0\) завжди працюватиме. Але щоб зробити рішення правильним для конкретного аналізу напружень, граничні умови на напруження і зміщення повинні бути виконані також. Зазвичай це набагато складніше починання, і жодного загального рішення, яке працює для всіх випадків, не існує. Однак можна показати, що рішення, що задовольняє як рівнянню сумісності, так і граничним умовам, є унікальним; тобто це єдино правильне рішення.
Напруження навколо круглого отвору
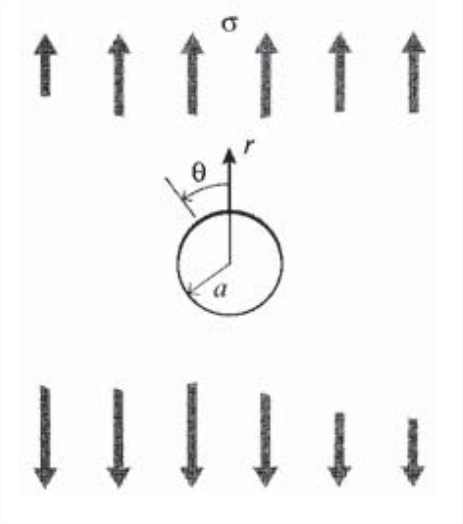
Для ілюстрації використання підходу функції Ейрі окреслимо важливу роботу Кірша (G. Kirsch, VDI, vol. 42, 1898; описана в Timoshenko & Goodier, op. cit..), який отримав рішення для впливу на напруження отвору, розміщеного в матеріалі. Це життєво важливо при аналізі таких проблем, як отвори для заклепок, що використовуються при з'єднанні, та вплив виробничої порожнечі на ініціювання відмови. Розглянемо тонкий аркуш, як показано на малюнку\(\PageIndex{2}\), нескінченний в бічних розмірах, але містить круглий отвір радіуса\(a\), і піддається одновісному напруженню\(\sigma\). Використовуючи кругові\(r, \theta\) координати, центровані на отворі, рівняння сумісності для\(\phi\)
\[\nabla^4 \phi = (\dfrac{\partial^2}{\partial r^2} + \dfrac{1}{r}\dfrac{\partial}{\partial r} + \dfrac{1}{r^2}\dfrac{\partial^2}{\partial \theta^2}) (\dfrac{\partial^2 \phi}{\partial r^2} + \dfrac{1}{r}\dfrac{\partial \phi}{\partial r} + \dfrac{1}{r^2}\dfrac{\partial^2 \phi}{\partial \theta^2}) = 0\]
У цих кругових координатах напруження отримують від\(\phi\) як
\[\begin{array} {rcl} {\sigma_r} & = & {\dfrac{1}{r}\dfrac{\partial \phi}{\partial r} + \dfrac{1}{r^2}\dfrac{\partial^2 \phi}{\partial \theta^2}} \\ {\sigma_{\theta}} & = & {\dfrac{\partial^2 \phi}{\partial r^2}} \\ {\tau_{r\theta}} & = & {-\dfrac{\partial}{\partial r} (\dfrac{1}{r} \dfrac{\partial \phi}{\partial \theta})} \end{array}\]
Тепер ми шукаємо функцію\(\phi (r, \theta)\), яка задовольняє рівнянню 5.1.13, а також граничним умовам задачі. На периферії отвору радіальні і зсувні напруги повинні зникнути, так як ніяких зовнішніх тяг там не існує:
\[\sigma_r = \tau_{r \theta} = 0, r = a\]
Далеко від отвору напруження повинні стати значенням далекого поля\(\sigma\); процедура Мора дає радіальні та тангенціальні компоненти напружень у кругових координатах як
\[\left \{ \begin{array} {rcl} {\sigma_r} & = & {\tfrac{\sigma}{2}(1 + \cos 2 \theta)} \\ {\sigma_{\theta}} & = & {\tfrac{\sigma}{2} (1 - \cos 2 \theta)} \\ {\tau_{r\theta}} & = & {\tfrac{\sigma}{2} \sin 2 \theta} \end{array} \right\} r \to \infty\]
Оскільки нормальні напруження змінюються по колу, оскільки\(\cos 2\theta\) (тимчасово\(\sigma/2\) усуваючи коефіцієнт), а напруження зсуву змінюються як\(\sin 2\theta\), прийнятна функція напружень може мати вигляд
\[\phi = f(r) \cos 2 \theta\]
Коли це підставляється в Рівняння 5.1.13, виходить звичайне диференціальне\(f(r)\) рівняння в:
\[\left(\frac{d^{2}}{d r^{2}}+\frac{1}{r} \frac{d}{d r}-\frac{4}{r^{2}}\right)\left(\frac{d^{2} f}{d r^{2}}+\frac{1}{r} \frac{d f}{d r}-\frac{4 f}{r^{2}}\right)=0\]
Це має загальне рішення
\[f(r) = Ar^2 + Br^4 + C \dfrac{1}{r^2} + D\]
Функція напружень, отримана з Eqns. 5.1.17 і 5.1.18, тепер використовується для запису виразів для напружень відповідно до Рівняння 5.1.14, а константи, визначені за граничними умовами в Eqns. 5.1.15 і 5.1.16; це дає
\[A=-\frac{\sigma}{4}, \quad B=0, \quad C=-\frac{a^{4} \sigma}{4}, \quad D=\frac{a^{2} \sigma}{2}\]
Підставляючи ці значення в вирази для наголосу і замінивши тимчасово видалене, кінцеві вирази для напружень є\(\sigma /2\)
\[\begin{array} {rcl} {\sigma_r} & = & {\dfrac{\sigma}{2} (1 - \dfrac{a^2}{r^2}) + \dfrac{\sigma}{2} (1 + \dfrac{3a^4}{r^4} - \dfrac{4a^2}{r^2}) \cos 2 \theta} \\ {\sigma_{\theta}} & = & {\dfrac{\sigma}{2} (1 + \dfrac{a^2}{r^2}) - \dfrac{\sigma}{2} (1 + \dfrac{3a^4}{r^4}) \cos 2 \theta} \\ {\tau_{r \theta}} & = & {-\dfrac{\sigma}{2} (1 - \dfrac{3a^4}{r^4} + \dfrac{2a^2}{r^2}) \sin 2 \theta} \end{array}\]
Як видно на графіку малюнка\(\PageIndex{1}\), напруга досягає максимального значення\((\sigma_{\theta})_{\max} = 3\sigma\) на периферії отвору (\(r = a\)), при діаметральному положенні поперечному напрямку навантаження (\(\theta = \pi /2\)). Тому коефіцієнт концентрації стресу, або SCF, для цієї проблеми становить 3. Напруга\(x\) -напрямок падає до нуля в положенні\(\theta = \pi /2\)\(r = a\), так як воно повинно задовольняти безнапруженій граничній умові на периферії отвору.

Зверніть увагу, що в разі круглого отвору СКФ не залежить від розміру отвору: будь-який отвір, яким би маленьким не було, збільшує місцеві напруги біля отвору в три рази. Це дуже серйозний розгляд при проектуванні конструкцій, які необхідно свердлити і клепати при складанні. Це стосується конструкції більшості фюзеляжів реактивних лайнерів, обшивка яких повинна витримувати значні навантаження, оскільки перепад тиску в салоні циклікується приблизно на 10 фунтів на квадратний дюйм під час кожного польоту. Область високої напруги біля отворів для заклепок має небезпечну схильність до інкубації втомних тріщин, і кілька катастрофічних відмов літаків простежено саме до цієї причини.
Зверніть увагу також, що ефект концентрації напружень обмежується областю, досить близькою до отвору, при цьому напруження падає до їх значень далекого поля в межах трьох або близько того діаметрів отвору. Це прояв принципу Сен-Венана (Французький вчений Барр де Сен-Венан (1797—1886) є одним із великих піонерів механіки матеріалів.), який є твердженням здорового глузду про те, що вплив збурень у полі напружень значною мірою обмежується областю збурень. Цей принцип надзвичайно корисний в інженерних наближеннях, але, звичайно, слід пам'ятати про концентрацію напруги поблизу самого порушення.
Коли на початку цього розділу ми взяли розмір пластини «нескінченним у бічній протяжності», ми дійсно мали на увазі, що умови напруги на краях пластини були досить далеко від отвору, щоб вони не впливали на напружений стан біля отвору. З рішенням Кірша зараз в руці, ми можемо бути більш реалістичними щодо цього: пластина повинна бути в три або близько того рази більше отвору, інакше рішення Кірша буде ненадійним.
складні функції
У багатьох задачах, що представляють практичний інтерес, зручно використовувати функції напружень як складні функції двох змінних. Ми побачимо, що вони мають здатність задовольняти керуючі рівняння автоматично, залишаючи лише коригування, необхідні для відповідності граничним умовам. З цієї причини складні змінні методи відіграють важливу роль в теоретичному аналізі напружень, і навіть у цьому вступному лікуванні ми хочемо проілюструвати силу методу. Щоб окреслити кілька необхідних відносин, вважайте\(z\) комплексне число в декартових координатах\(x\)\(y\) та/або полярних координатах\(r\) і\(\theta\) як
\[z = x + iy = r^{i \theta}\]
де\(i = \sqrt{-1}\). Аналітична функція\(f(z)\) - це та, похідні якої залежать\(z\) тільки від, і набуває вигляду
\[f(z) = \alpha + i \beta\]
де\(\alpha\) і\(\beta\) знаходяться реальні функції\(x\) і\(y\). Легко показано, що\(\alpha\) і\(\beta\) задовольняють рівняння Коші-Рімана:
\[\dfrac{\partial \alpha}{\partial x} = \dfrac{\partial \beta}{\partial y}\ \ \ \ \ \dfrac{\partial \alpha}{\partial y} = -\dfrac{\partial \beta}{\partial x}\]
Якщо перший з них диференціюється по відношенню до,\(x\) а другий по відношенню до\(y\), а результати додаються, ми отримуємо
\[\dfrac{\partial^2 \alpha}{\partial x^2} + \dfrac{\partial^2 \alpha}{\partial y^2} \equiv \nabla^2 \alpha = 0\]
Це рівняння Лапласа, і будь-яка функція, яка задовольняє цьому рівнянню, називається гармонічною функцією. Аналогічно,\(\alpha\) можна було б усунути на користь\(\beta\) дати\(\nabla^2 \beta = 0\), тому як реальна, так і уявна частини будь-якої складної функції забезпечують розв'язки рівняння Лапласа. Тепер розглянемо функцію форми\(x \psi\), де\(\psi\) гармоніка; це може бути показано прямою диференціацією, що
\[\nabla^4 (x \psi) = 0\]
тобто будь-яка функція виду\(x\psi\), де\(\psi\) є гармонійною, задовольняє рівнянню 5.1.12, і багато хто, таким чином, використовується як функція напружень. Аналогічним чином можна показати, що\(y \psi\) і теж\((x^2 + y^2) \psi = r^2 \psi\) підходять, як є\(\psi\) сам. Загалом, відповідну функцію напруги можна отримати з будь-яких двох аналітичних функцій\(\psi\) і\(\chi\) відповідно до
\[\phi = \text{Re} [(x - iy) \psi (z) + \chi (z)]\]
де "\(\text{Re}\)" вказує на реальну частину складного виразу. Напруги, відповідні цій функції\(\phi\), отримують як
\[\begin{array} {rcl} {\sigma_x + \sigma_y} & = & {4 \text{Re} \psi' (z)} \\ {\sigma_y - \sigma_x + 2 i \tau_{xy}} & = & {2 [\bar{z} \psi '' (z) + \chi '' (z)]} \end{array}\]
де прості числа вказують на диференціювання по відношенню до,\(z\) а овербар вказує на сполучену функцію, отриману\(i\) заміною на\(-i\); отже\(\bar{z} = x - iy\).
Напруження навколо еліптичного отвору
У розробці, дуже важливій для теорії руйнування, Інгліс (C.E. Inglis, «Напруження в плиті через наявність тріщин і гострих кутів», транзакції Інституту військово-морських архітекторів, Vol. 55, Лондон, 1913, стор. 219—230.) використовував складні потенційні функції для розширення роботи Кірша для лікування поле напружень навколо пластини, що містить еліптичний, а не круглий отвір. Це дозволяє обробляти тріщиноподібні геометрії, роблячи незначну вісь еліпса невеликою. Зручно працювати в еліптичних\(\alpha, \beta\) координатах, як показано на малюнку 4, визначеному як
\[x = c \cosh \alpha \cos \beta, y = c \sin h \alpha \sin \beta\]
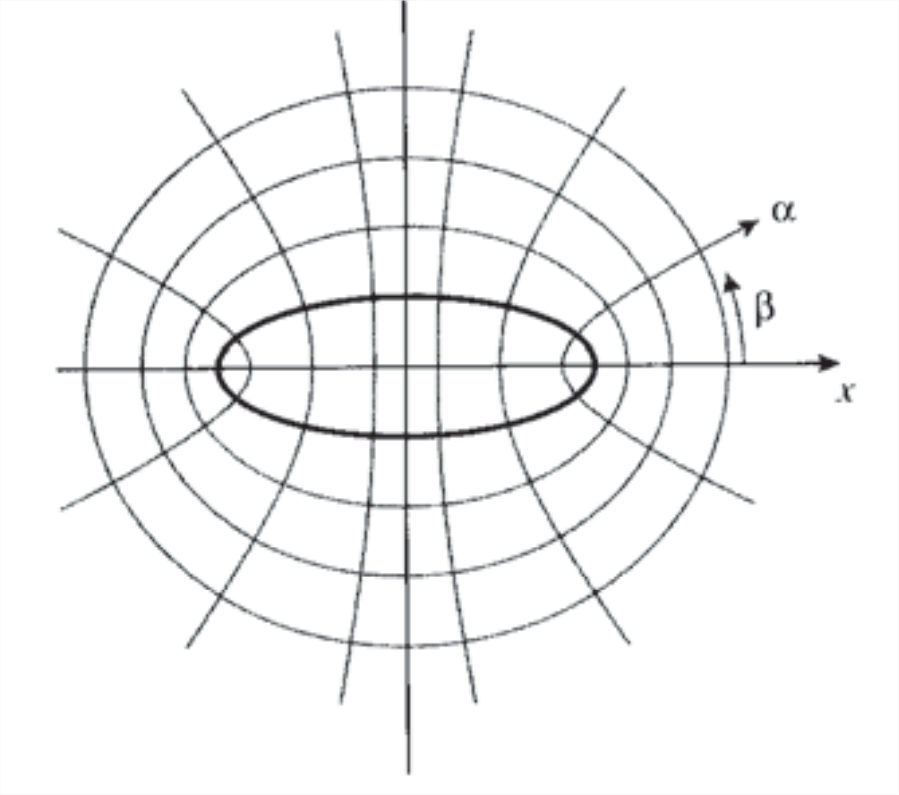
де\(c\) константа. Якщо\(\beta\) усувається, це, в свою чергу, буде еквівалентно
\[\dfrac{x^2}{\cosh^2 \alpha} + \dfrac{y^2}{\sinh^2 \alpha} = c^2\]
На кордоні еліпса\(\alpha = \alpha_0\), так що ми можемо написати
\[c \cosh \alpha_0 = a, c \sinh \alpha_0 = b\]
де\(a\) і\(b\) є константами. На кордоні, то
\[\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\]
який визнається декартовим рівнянням еліпса, з великим\(a\) і\(b\) малим радіусами. Еліптичні координати можуть бути записані в терміні комплексних змінних як
\[z = c \cosh \zeta, \ \ \ \ \zeta = \alpha + i \beta\]
Оскільки межа еліпса проходить,\(\alpha\) залишається постійною в той\(\alpha_0\) час як\(\beta\) змінюється від 0 до\(2\pi\). Звідси напруги повинні бути періодичними в\(\beta\) з періодом\(2\pi\), при цьому дорівнюючи одновісному напруженню далекого поля\(\sigma_y = \sigma, \sigma_x = \tau_{xy} = 0\) далеко від еліпса; Рівняння 5.1.26 тоді дає
\[\left \{ \begin{array} {rcl} {4 \text{Re} \psi ' (z)} & = & {\sigma} \\ {2[\bar{z} \psi '' (z) + \chi '' (z)]} & = & {\sigma} \end{array} \right \} \zeta \to \infty\]
Ці граничні умови можуть задовольнятися потенційними функціями у формах.
\(\begin{array} {rcl} {4 \psi (z)} & = & {Ac \cosh \zeta + Bc \sinh \zeta} \\ {4 \chi (z)} & = & {Cc^2 \zeta + Dc^2 \cosh 2 \zeta + Ec^2 \sinh 2 \zeta} \end{array}\)
де\(A,B,C,D,E\) константи, які слід визначати з граничних умов. Коли це робиться, складні потенціали задаються як
\[4 \psi(z)=\sigma c\left[\left(1+e^{2 \alpha_{0}}\right) \sinh \zeta-e^{2 \alpha_{0}} \cosh \zeta\right]\]
\[4 \chi(z)=-\sigma c^{2}\left[\left(\cosh 2 \alpha_{0}-\cosh \pi\right) \zeta+\frac{1}{2} e^{2 \alpha_{0}}-\cosh 2\left(\zeta-\alpha_{0}-i \frac{\pi}{2}\right)\right]\]
Напруги\(\sigma_x, \sigma_y\), і\(\tau_{xy}\) можуть бути отримані, використовуючи їх в Eqns. Однак кількість праці при здійсненні цих замін не слід чхати, і до того, як комп'ютери були загальнодоступні, рішення Inglis мало дещо обмежене використання в зондуванні природи стресового поля поблизу кінчиків тріщин.
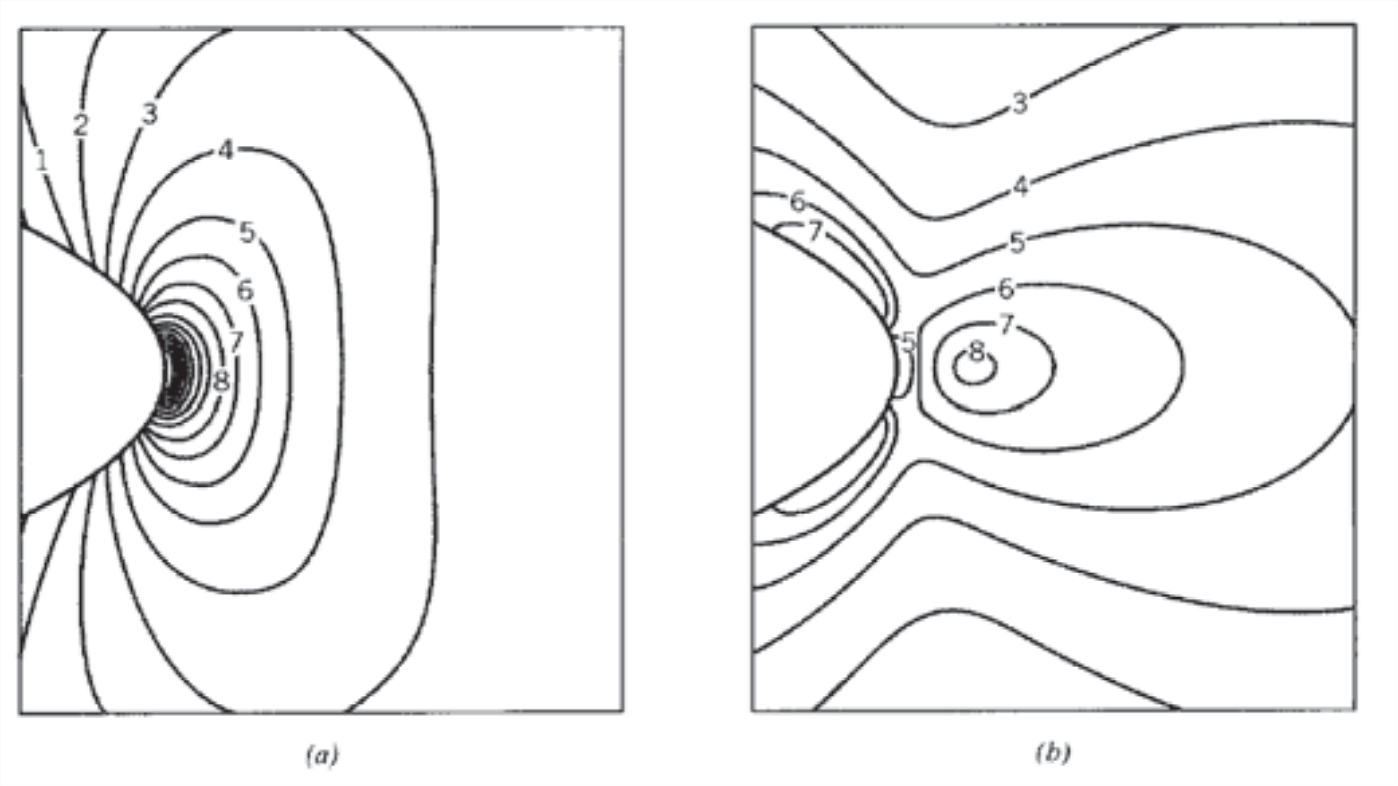
Малюнок 5: Поле напружень поблизу еліптичного отвору, з одновісним напруженням, застосованим у\(y\) -напрямку. (а) Контури\(\sigma_y\), (б) Контури\(\sigma_x\).
На малюнку 5 показані контури напружень, обчислені Куком та Гордоном (J.E. Gordon, Наука про структури та матеріали, Наукова американська бібліотека, Нью-Йорк, 1988.) з рівнянь Інгліса. Сильна напружена концентрація напруги\(\sigma_y\) відзначається на периферії отвору, як і слід було очікувати. Горизонтальне напруження\(\sigma_x\) йде до нуля в цьому ж положенні, так як воно повинно задовольняти там граничні умови. Зверніть увагу, однак, що\(\sigma_x\) демонструє м'яку концентрацію стресу (одна п'ята частина цього для\(\sigma_y\), виявляється) на невеликій відстані від отвору. Якщо матеріал має площини слабкості вздовж\(y\) напрямку, наприклад, між фібрилами в деревині або багатьма іншими біологічними структурами, напруга\(\sigma_x\) може спричинити розкол, щоб відкрити в\(y\) напрямку попереду основної тріщини. Це буде діяти, щоб затупити і затримати тріщину, і, таким чином, надати матеріалу міру в'язкості. Цей ефект іноді називають механізмом зміцнення Кука-Гордона.
Математика рішення Інгліса простіше на поверхні еліптичної діри, так як тут нормальна складова\(\sigma_{\alpha}\) повинна зникнути. Потім компонент тангенціального напруження можна обчислити безпосередньо:
\[\left(\sigma_{\beta}\right)_{\alpha=\alpha_{0}}=\sigma e^{2 \alpha_{0}}\left[\frac{\sinh 2 \alpha_{0}\left(1+e^{-2 \alpha_{0}}\right)}{\cosh 2 \alpha_{0}-\cos 2 \beta}-1\right]\]
Найбільша напруга виникає в кінці великої осі\((\cos 2 \beta = 1)\):
\[(\sigma_{\beta})_{\beta = 0, \pi} = \sigma_y = \sigma (1 + 2 \dfrac{a}{b})\]
Це також може бути записано через радіус кривизни\(\rho\) на кінчику великої осі як
\[\sigma_y = \sigma (1 + 2 \sqrt{\dfrac{a}{\rho}})\]
Такий результат відразу стане в нагоді: зрозуміло, що великі тріщини гірше дрібних (місцеве напруження збільшується з розміром тріщин\(a\)), а також очевидно, що гострі порожнечі (зменшуються\(\rho\)) гірше округлих. Зверніть увагу також, що напруга\(\sigma_y\) збільшується без обмеження, оскільки тріщина стає більш різкою (\(\rho \to 0\)), тому поняття коефіцієнта концентрації напружень стає важко використовувати для дуже гострих тріщин. Коли великі та малі осі еліпса однакові (\(b = a\)), результат стає ідентичним результату круглого отвору, окресленого раніше.
Напруження біля гострої тріщини
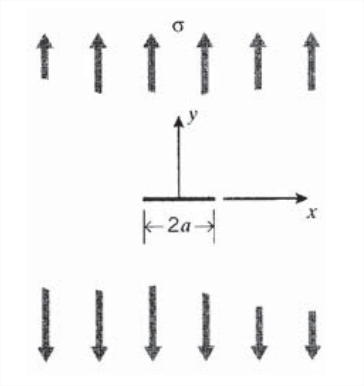
Малюнок 6: Гостра тріщина в нескінченному аркуші.
Розчин Інгліс складно наносити, тим більше, що тріщина стає гострою. Більш гнучкий і тепер більш широко використовуваний підхід був розроблений Westergaard (Westergaard, H.M., «Несучі тиску і тріщини», Транзакції, Am. Соц. Мех. Енгр., Journal of Applied Mechanics, Vol. 5, стор. 49, 1939.), який обробляє гостру тріщину довжиною\(2a\) в тонкому, але нескінченно широкому аркуші (див. Рис. Напруження, що діють перпендикулярно до вільних від тріщин поверхонь (тріщини «фланги»), повинні дорівнювати нулю, в той час як на віддалених від тріщини відстанях вони повинні наближатися до далекому полю накладених напружень. Розглянемо гармонічну функцію\(\phi (z)\), з першим і другим похідними\(\phi '(z)\) і\(\phi '' (z)\), і першим і другим інтегралами\(\bar{\phi} (z)\) і\(\bar{\bar{\phi}}(z)\). Вестергард побудував функцію стресу як
\[\Phi = \text{Re} \bar{\bar{\phi}} (z) + y \text{Im} \bar{\phi} (z)\]
Безпосередньо можна показати, що напруги, отримані від цієї функції, задовольняють рівновагу, сумісність і конститутивні відносини. Функція,\(\phi (z)\) необхідна тут, є гармонійною функцією, такою, що напруження наближаються до значення далекого поля\(\sigma\) на нескінченності, але дорівнюють нулю на флангах тріщини, за винятком кінчика тріщини, де напруга стає необмеженою:
\(\sigma_y = \begin{cases} \sigma, x \to \pm \infty, -a < x < + a,y = 0 \\ \infty, x = \pm \infty \end{cases}\)
Цим умовам задовольняють складні функції форми.
\[\phi (z) = \dfrac{\sigma}{\sqrt{1 - a^2/z^2}}\]
Це дає необхідну сингулярність для\(z = \pm a\), а інші граничні умови можуть бути перевірені безпосередньо. Напруження тепер знаходять відповідними диференціаціями функції напружень; наприклад
\(\sigma_y = \dfrac{\partial^2 \Phi}{\partial x^2} = \text{Re} \phi (z) + y \text{Im} \phi ' (z)\)
З точки зору відстані\(r\) від кінчика тріщини це стає
\[\sigma_y = \sigma \sqrt{\dfrac{a}{2r}} \cdot \cos \dfrac{\theta}{2} (1 + \sin \dfrac{\theta}{2} \sin \dfrac{3\theta}{2}) + \cdots\]
де це початкові члени наближення ряду. Близько тріщини кінчик, коли\(r \ll a\), можемо написати
\[(\sigma_y)_{y = 0} = \sigma \sqrt{\dfrac{a}{2r}} \equiv \dfrac{K}{\sqrt{2 \pi r}}\]
де\(K = \sigma \sqrt{\pi a}\) - коефіцієнт інтенсивності напружень, з одиницями\(Nm^{-3/2}\) або\(\text{psi} \sqrt{\text{in}}\). (Коефіцієнт\(\pi\) здається надмірним тут, оскільки він здається однаковою силою як у чисельнику, так і в знаменнику, але він зазвичай включається так, як написано тут для узгодження зі старою літературою.) Ми побачимо в Модулі про руйнування, що коефіцієнт інтенсивності напружень є загальноприйнятою мірою рушійної сили для поширення тріщин, і, таким чином, лежить в основі більшої частини сучасної механіки руйнування. Залежність напруги від відстані від тріщини є сингулярною, з\(1/\sqrt{r}\) залежністю. Фактор K масштабує інтенсивність загального розподілу напружень, при цьому напруга завжди стає необмеженою, коли наближається кінчик тріщини.
Вправа\(\PageIndex{1}\)
Розгорніть керівні рівняння (Eqns. 5.1.1 - 5.1.3) в двох декартових вимірах. Визначте невідомі функції. Скільки рівнянь і невідомих існує?
Вправа\(\PageIndex{2}\)
Розглянемо товстостінний посудину під тиском внутрішнього радіуса\(r_i\) і зовнішнього радіуса\(r_o\), що піддається внутрішньому тиску\(p_i\) і зовнішньому тиску\(p_o\).
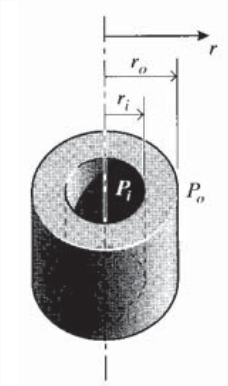
Припустимо пробне рішення для радіального зміщення форми\(u(r) = Ar + B/r\); це співвідношення може бути показано, що задовольняє керуючі рівняння рівнянь рівноваги, деформації та напруження-деформації рівнянь.
(a) Оцінити константи\(A\) і\(B\) використовувати граничні умови
\[\sigma_r = -p_i @ r = r_i, \sigma_r = -p_0 @ r = r_o\]
(б) Потім покажіть, що
\[\sigma_{r}(r)=-\frac{p_{i}\left[\left(r_{o} / r\right)^{2}-1\right]+p_{o}\left[\left(r_{o} / r_{i}\right)^{2}-\left(r_{o} / r\right)^{2}\right]}{\left(r_{o} / r_{i}\right)^{2}-1}\]
Вправа\(\PageIndex{3}\)
Обґрунтувати граничні умови, наведені в Eqns. 5.1.14 для напружень в кругових координатах (\(\sigma_r, \sigma_{\theta}, \tau_{xy}\)), відповідних одноосно навантаженій пластині, що містить круглий отвір.
Вправа\(\PageIndex{4}\)
Показати, що функція Ейрі,\(\phi (x, y)\) визначена Eqns. 5.1.11 задовольняє рівнянням рівноваги.
Вправа\(\PageIndex{5}\)
Показати, що функції напружень у вигляді квадратичних або кубічних многочленів\((\phi = a_2 x^2 + b_2 xy + c_2 y^2\) і\(\phi = a_3 x^3 + b_3 x^2 y + c_3 xy^2 + d_3 y^3\)) автоматично задовольняють керуючому співвідношенню\(\nabla^4 \phi = 0\).
Вправа\(\PageIndex{6}\)
Запишіть напруження, що\(\sigma_x, \sigma_y, \tau_{xy}\) відповідають квадратичним і кубічним функціям напружень попередньої задачі.
Вправа\(\PageIndex{7}\)
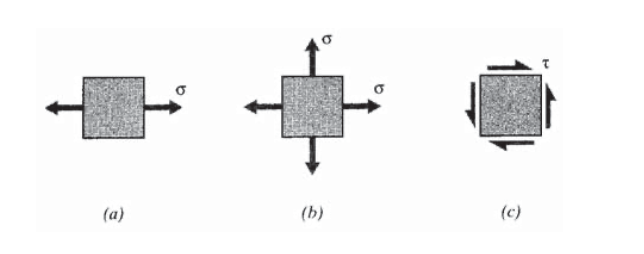
Виберіть константи у квадратичній функції напружень попередніх двох задач таким чином, щоб представляти (а) простий натяг, (b) двовісний натяг та (c) чистий зсув прямокутної пластини.
Вправа\(\PageIndex{8}\)
Виберіть константи у функції кубічних напружень попередніх задач таким чином, щоб представляти чистий вигин, індукований парами, застосованими до вертикальних сторін прямокутної пластини.

Вправа\(\PageIndex{9}\)
Розглянемо консольну балку прямокутного перерізу і ширини\(b = 1\), навантажену на вільний кінець (\(x = 0\)) із зусиллям\(P\). На вільному кінці можуть бути записані граничні умови на напругу\(\sigma_x = \sigma_y = 0\), і
\(\int_{-h/2}^{h/2} \tau_{xy} \ dy = P\)
Горизонтальні краї не завантажуються, тому ми також маємо, що\(\tau_{xy} = 0\) в\(y = \pm h/2\).
(а) Показати, що ці умови задовольняються стресовою функцією форми
\(\phi = b_2 xy + d_4 xy^3\)
(b) Оцініть константи, щоб показати, що напруги можуть бути записані
\[\sigma_{x}=\frac{P x y}{I}, \quad \sigma_{y}=0, \quad \tau_{x y}=\frac{P}{2 I}\left[\left(\frac{h}{2}\right)^{2}-y^{2}\right]\]
за погодженням з елементарною теорією вигину балки (Модуль 13).