5.4: Метод суглобів

Last updated
Save as PDF

Page ID: 31098

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Метод з'єднань - це процес, який використовується для вирішення невідомих сил, що діють на елементи ферми. Метод зосереджується на стиках або точках з'єднання між елементами, і це, як правило, найшвидший і простий спосіб вирішити всі невідомі сили в кроквяній конструкції.

Використання методу суглобів:

Процес, який використовується в методі швів, викладено нижче.

На початку зазвичай корисно позначити елементи та стики у вашій фермі. Це допоможе вам зберегти все організовано та послідовно в подальшому аналізі. У цій книзі члени будуть позначені буквами, а стики будуть позначені цифрами.

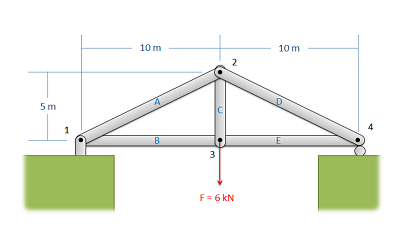
Вид збоку моста з 20-метровим прольотом, розділеним на ділянки В (зліва) і Е (праворуч) в точці 3 нижнім кінцем 5-метрової вертикальної балки С. Лівий кінець Б (точка 1) з'єднаний з верхнім кінцем С (точка 2) діагональною балкою А. Правий кінець Е (точка 4) з'єднаний з точкою 2 а Діагональний промінь D Точка 3 відчуває зусилля вниз 6 кН. Точки 1 і 4 утримуються від землі штифтовим з'єднанням і роликовим з'єднанням відповідно. — Малюнок\(\PageIndex{1}\): Першим кроком методу з'єднань є маркування кожного суглоба і кожного елемента.

Розглядаючи всю кроквяну конструкцію як жорстке тіло, намалюйте діаграму вільного тіла, випишіть рівняння рівноваги та вирішіть для зовнішніх реагуючих сил, що діють на кроквяну конструкцію. Цей аналіз не повинен відрізнятися від аналізу єдиного жорсткого тіла.

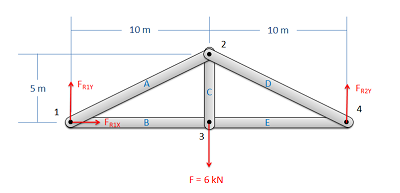
На малюнку 1 розділу вище показано реакційні сили на ньому: точка 1 відчуває силу реакції як з горизонтальними (x), так і вертикальними (y) компонентами; точка 4 відчуває силу реакції лише з компонентом y. — Малюнок\(\PageIndex{2}\): Обробіть всю ферму як жорстке тіло і вирішуйте сили реакції, що підтримують кроквяну конструкцію.

Припустимо, що в кожній з точок з'єднання між елементами є штифт або якась інша невелика кількість матеріалу. Далі ви намалюєте вільну схему тіла для кожної точки підключення. Не забудьте включити:

Будь-яка зовнішня реакція або сили навантаження, які можуть діяти на цей суглоб.
Нормальна сила для кожного двох силових елементів, з'єднаних з цим суглобом. Пам'ятайте, що для двох силових елементів сила буде діяти по лінії між двома точками з'єднання на елементі. Нам також потрібно буде вгадати, чи буде це розтягуюча або стискаюча сила. Неправильне припущення зараз, хоча пізніше просто призведе до негативного рішення. Загальна стратегія тоді полягає в тому, щоб припустити, що всі сили розтягуються, то пізніше в розчині будь-які позитивні сили будуть розтягуючими силами, а будь-які негативні сили будуть стискаючими силами.
Позначте кожну силу на схемі. Включіть будь-які відомі величини та напрямки та надайте імена змінних для кожного невідомого.

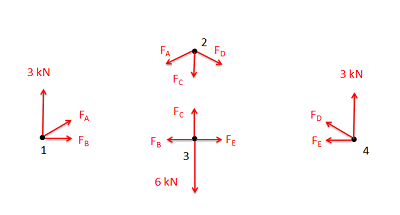
Вільні діаграми тіла точок 1, 2, 3 і 4 з рис. 1 і 2 вище. Точки 1 і 4 кожен відчувають висхідну силу 3 кН; точка 3 відчуває силу вниз 6 кН. Крім того, кожна точка відчуває силу натягу для кожного елемента, який до неї прикріплений. — Малюнок\(\PageIndex{3}\): Малюючи вільну діаграму тіла кожного суглоба, малюємо відомі сили, а також сили розтягування від кожного двосилового елемента.

Випишіть рівняння рівноваги для кожного з суглобів. Ви повинні розглядати суглоби як частинки, тому будуть рівняння сили, але не рівняння моменту. З двома (для 2D-задач) або трьома (для 3D-задач) рівняннями для кожного суглоба; це повинно дати вам велику кількість рівнянь.
- У плоских фермах сума сил в\(x\) напрямку буде дорівнює нулю і сума сил в\(y\) напрямку буде дорівнює нулю для кожного з стиків. \[ \sum \vec{F} = 0 \]\[ \sum F_x = 0 \, ; \,\,\, \sum F_y = 0 \]
- У просторових фермах сума сил в\(x\) напрямку буде дорівнює нулю, сума сил в\(y\) напрямку буде дорівнює нулю, а сума сил в\(z\) напрямку буде дорівнює нулю для кожного з стиків. \[ \sum \vec{F} = 0 \]\[ \sum F_x = 0 \, ; \,\,\, \sum F_y = 0 \, ; \,\,\, \sum F_z = 0 \]
Нарешті, вирішіть рівняння рівноваги для невідомих. Ви можете зробити це алгебраїчно, вирішуючи для однієї змінної за раз, або ви можете використовувати матричні рівняння для вирішення всього відразу. Якщо ви припускали, що всі сили були розтягуються раніше, пам'ятайте, що негативні відповіді вказують на стискаючі сили в членах.

Відеолекція, що охоплює цей розділ, прочитана доктором Джейкобом Муром. Джерело YouTube: https://youtu.be/B8SEG7xPI-o.

Приклад\(\PageIndex{1}\)

Знайдіть силу, що діє в кожному з елементів кроквяного моста, показаного нижче. Не забудьте вказати, чи кожен член знаходиться в напрузі або стисненні.

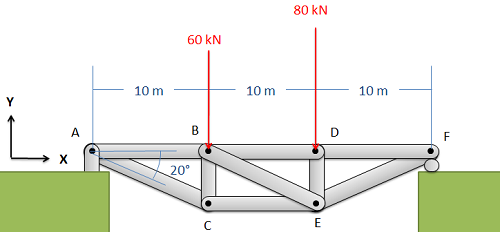
Фермовий міст, що охоплює 30 метрів; крайній лівий кінець, точка А, спирається на землю на штифтове з'єднання, а крайній правий кінець, точка F, спирається на землю на роликовому шарнірі. A і F - це кожна кінцева точка 10-метрових членів, з'єднаних іншим 10-метровим горизонтальним елементом з лівою кінцевою точкою B і правою кінцевою точкою D. Член BD є самим верхнім краєм прямокутника, інші сторони якого утворені членами BC, CE та ED. Точки А і С з'єднані елементом, який робить кут 20° з горизонталлю, так само як і точки Е і F. В точці B прикладається сила вниз 60 кН, а сила вниз 80 кН прикладається в точці D. — Малюнок\(\PageIndex{4}\): діаграма проблеми для Приклад\(\PageIndex{1}\). Кроквяний міст представлений у вигляді 2D площини ферми, зі стандартною\(xy\) орієнтаційною системою координат.

Рішення: Відео\(\PageIndex{2}\): Опрацьоване рішення прикладної проблеми\(\PageIndex{1}\), надане доктором Джейкобом Муром. Джерело YouTube: https://youtu.be/vowewkEdTzw.

Приклад\(\PageIndex{2}\)

Знайдіть силу, що діє в кожному з елементів ферми, показаних нижче. Не забудьте вказати, чи кожен член знаходиться в напрузі або стисненні.

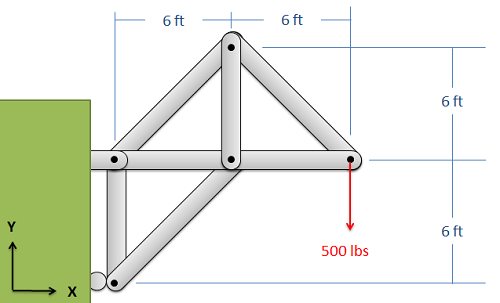
Ферма складається з горизонтальної секції довжиною 12 футів, яка прикріплена до стіни на її лівому кінці штифтовим з'єднанням і складається з 2 6-футових елементів; вертикальний елемент довжиною 6 футів, прикріплений на його нижньому кінці до середини горизонтальних елементів; два діагональні елементи, що прикріплюють верхній кінець зазначеної вертикалі елемент на лівому і правому кінцях 12-футового прольоту; другий 6-футовий вертикальний елемент прикріплений на лівому кінці 12-футового прольоту і поширюється вниз, так що його нижній кінець прикріплений до стіни за допомогою роликового з'єднання; і діагональний елемент, що з'єднує кінець роликового суглоба з середньою точкою 12-футового прольоту. Зниження сили 500 фунтів застосовується на правому кінці горизонтального прольоту. — Малюнок\(\PageIndex{5}\): діаграма проблеми для Приклад\(\PageIndex{2}\). Плоска ферма, встановлена на стіні, з\(xy\) стандартно-орієнтаційною системою координат.

Рішення: Відео\(\PageIndex{3}\): Опрацьоване рішення прикладної проблеми\(\PageIndex{2}\), надане доктором Джейкобом Муром. Джерело YouTube: https://youtu.be/IxnClZ-ppjM.

Приклад\(\PageIndex{3}\)

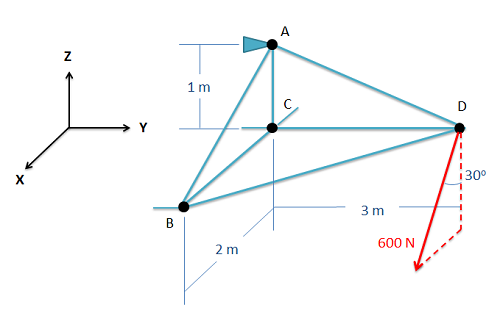
У yz-площині (площині екрану) точка C знаходиться на початку, точка A - на 1 метр вище C, а точка D - 3 метри праворуч від C, причому всі 3 точки з'єднані членами, утворюючи прямокутний трикутник. На осі х, що вказує на екран, точка B дорівнює 2 метрам вперед від C; B з'єднується членами до точок A, C і D. У точці D сила 600 Н прикладається вниз (у негативному напрямку z) і поза екраном, роблячи кут 30° з YZ-площиною. Вся ферма підтримується кульово-розетковим з'єднанням, основа якого вказує в негативному напрямку y, в точці А. — Малюнок\(\PageIndex{6}\): діаграма проблеми для Приклад\(\PageIndex{3}\). Простір ферма підтримується єдиним шарніром і гніздо, орієнтованим на 3D систему координат з\(yz\) -площиною в площині екрану і\(x\) -вісь, що вказує на екран.

Рішення: Відео\(\PageIndex{4}\): Опрацьоване рішення прикладної проблеми\(\PageIndex{3}\), надане доктором Джейкобом Муром. Джерело YouTube: https://youtu.be/sDKESSbufEk.