5.5: Метод розділів

Last updated

Oct 25, 2022
Save as PDF
- 5.4: Метод суглобів
- 5.6: Рами та машини

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Метод секцій - це процес, який використовується для вирішення невідомих сил, що діють на елементи ферми. Метод передбачає розбивання ферми вниз на окремі ділянки і аналіз кожної секції як окремого жорсткого тіла. Метод секцій зазвичай є найшвидшим і простим способом визначення невідомих сил, що діють в конкретному елементі ферми.

Використання методу розділів:

Процес, який використовується в методі розрізів, викладено нижче.

На початку зазвичай корисно позначити елементи у вашій фермі. Це допоможе вам зберегти все організовано та послідовно в подальшому аналізі. У цій книзі члени будуть позначені буквами.

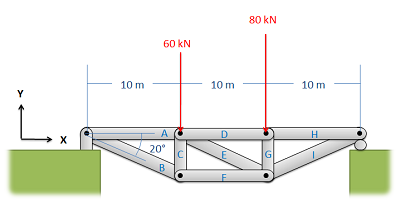
Малюнок $\PageIndex{1}$ : Першим кроком у методі секцій є маркування кожного члена.
Розглядаючи всю кроквяну конструкцію як жорстке тіло, намалюйте діаграму вільного тіла, випишіть рівняння рівноваги та вирішіть для зовнішніх реагуючих сил, що діють на кроквяну конструкцію. Цей аналіз не повинен відрізнятися від аналізу єдиного жорсткого тіла.

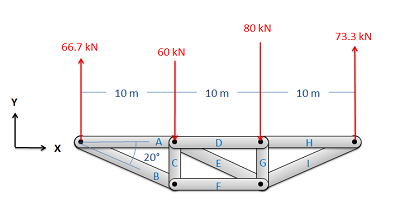
Малюнок $\PageIndex{2}$ : Обробіть всю ферму як жорстке тіло і вирішуйте сили реакції, що підтримують кроквяну конструкцію.
Далі ви уявляєте розрізання вашої ферми на дві окремі секції. Розріз повинен подорожувати через член, який ви намагаєтеся вирішити за сили в, і повинен прорізати якомога менше членів. Зріз не обов'язково повинен бути прямою лінією.

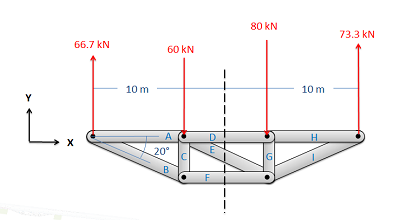Малюнок $\PageIndex{3}$ : Далі ви уявляєте розрізання ферми на дві частини. Якщо ви хочете знайти сили в конкретному члені, обов'язково проріжте цей член. Це також полегшує ситуацію, якщо ви прорізаєте якомога менше членів.
Далі ви намалюєте схему вільного тіла для одного або обох розділів, які ви створили. Обов'язково включайте всі сили, що діють на кожну секцію.
- Будь-яка зовнішня реакція або сили навантаження, які можуть діяти на ділянці.
- Внутрішня сила в кожному елементі, яка була розрізана при розбиванні ферми на секції. Пам'ятайте, що для двухсилового елемента сила буде діяти по лінії між двома точками з'єднання на елементі. Нам також потрібно буде вгадати, чи буде це розтягуюча або стискаюча сила. Однак неправильне припущення зараз просто призведе до негативного рішення пізніше. Загальна стратегія тоді полягає в тому, щоб припустити, що всі сили розтягуються; тоді пізніше в розчині будь-які позитивні сили будуть розтягуючими силами, а будь-які негативні сили будуть стискаючими силами.
- Позначте кожну силу на схемі. Включіть будь-які відомі величини та напрямки та надайте імена змінних для кожного невідомого.
  
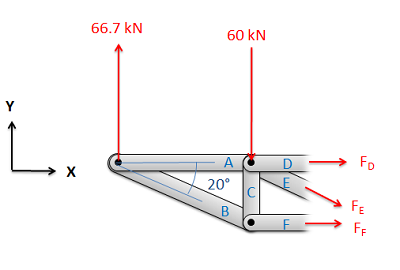
  Малюнок $\PageIndex{4}$ : Далі намалюйте схему вільного тіла однієї або обох половинок ферми. Додайте відомі сили, а також невідомі сили розтягування для кожного члена, який ви розрізаєте.
Випишіть рівняння рівноваги для кожного розділу ви намалювали діаграму вільного тіла. Це будуть розширені тіла, тому вам потрібно буде виписати рівняння сили і моменту.
- Для 2D-задач у вас буде три можливі рівняння для кожного розділу: два рівняння сили та одне рівняння моменту. $\sum \vec{F} = 0 \quad\quad\quad\quad \sum \vec{M} = 0$ $\sum F_x = 0 \, ; \,\,\, \sum F_y = 0 \, ; \,\,\, \sum M_z = 0$
- Для 3D-задач у вас буде шість можливих рівнянь для кожного розділу: три рівняння сили та три рівняння моменту. $\sum \vec{F} = 0$ $\sum F_x = 0 \, ; \,\,\, \sum F_y = 0 \, ; \,\,\, \sum F_z = 0$ $\sum \vec{M} = 0$ $\sum M_x = 0 \, ; \,\,\, \sum M_y = 0 \, ; \,\,\, \sum M_z = 0$
Нарешті, вирішіть рівняння рівноваги для невідомих. Ви можете зробити це алгебраїчно, вирішуючи для однієї змінної за раз, або ви можете використовувати матричні рівняння для вирішення всього відразу. Якщо ви припускали, що всі сили були розтягуються раніше, пам'ятайте, що негативні відповіді вказують на стискаючі сили в членах.

Відеолекція, що охоплює цей розділ, прочитана доктором Джейкобом Муром. Джерело YouTube: https://youtu.be/XcRn776w22Q.

Приклад $\PageIndex{1}$

Знайдіть сили, що діють на членів БД і СЕ. Обов'язково вкажіть, якщо зусилля розтягують або стискають.

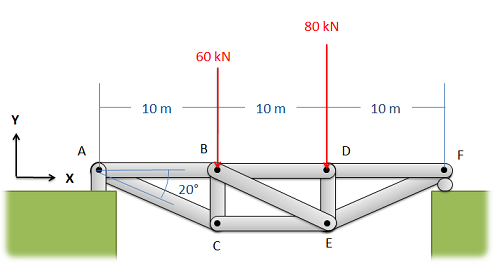
Фермовий міст з 30-метровим прольотом; крайній лівий кінець, точка А, з'єднується з землею штифтовим з'єднанням, а крайній правий кінець, F, з'єднується з землею роликовим з'єднанням. Проліт формується з 3-х 10-метрових горизонтальних елементів: AB, BD і DF. Два вертикальні елементи, BC і DE, прикріплюються до кінцевих точок центрального елемента цього прольоту і простягаються під ним. Інший горизонтальний елемент з'єднує точки C і E. Діагональні елементи змінного струму та FE, кожен на 20° нижче горизонтального, з'єднують кінці цього нижнього горизонтального елемента з кінцевими точками прольоту моста. У точці В прикладається сила вниз 60 кН, а в точці D прикладається сила вниз 80 кН. — Малюнок $\PageIndex{5}$ : діаграма проблеми для Приклад $\PageIndex{1}$ . Двовимірне уявлення кроквяного моста, зі стандартно-орієнтаційною $xy$ -системою координат.

Рішення: Відео $\PageIndex{2}$ : Опрацьоване рішення прикладної проблеми $\PageIndex{1}$ , надане доктором Джейкобом Муром. Джерело YouTube: https://youtu.be/9xxmHpLB1uU.

Приклад $\PageIndex{2}$

Знайдіть сили, що діють на члени AC, BC і BD ферми. Обов'язково вкажіть, якщо зусилля розтягують або стискають.

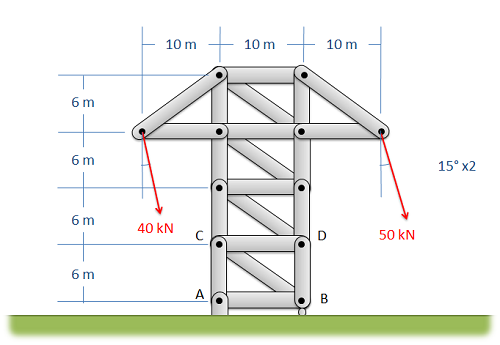
Вежа, що складається з ферм, розташованих у довгому прямокутнику, що складається з 4 однакових менших прямокутників, які кожен довжиною 10 м і висотою 6 м. Найнижчі точки вежі, А зліва і В праворуч, прикріплюються до землі штифтовим з'єднанням і роликовим з'єднанням відповідно. Точки С і D прикріплюються до А і В відповідно вертикальними членами, а В і С пов'язані діагональним елементом. З кожного боку нижнього горизонтального елемента самої верхньої прямокутної субодиниці горизонтально виступає 10-метровий елемент і діагональний елемент пов'язує вільний кінець виступу з відповідним верхнім кутом самого верхнього прямокутника. Кінцеві точки виступаючих елементів відчувають силу вниз і вправо, на 15° від вертикалі. Величина сили лівого члена дорівнює 40 кН, а величина правого члена - 50 кН. — Малюнок $\PageIndex{6}$ : Діаграма проблеми для Приклад $\PageIndex{2}$ . Двовимірне зображення вежі, складеної з ферм, розташованих у високому прямокутнику з прямокутної субодиниці з трапецієподібною вершиною.

Рішення: Відео $\PageIndex{3}$ : Опрацьоване рішення прикладної проблеми $\PageIndex{2}$ , надане доктором Джейкобом Муром. Джерело YouTube: https://youtu.be/Kp9U4d2qbvE.