5.3: Ферми

Last updated

Oct 25, 2022
Save as PDF
- 5.2: Члени двох сил
- 5.4: Метод суглобів

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Ферма - це інженерна конструкція, яка виконана повністю з двосилових елементів. Крім того, статично визначені ферми (ферми, які можна аналізувати повністю за допомогою рівнянь рівноваги) повинні бути незалежно жорсткими. Це означає, що якби ферма була відокремлена від місць її з'єднання, жодна частина не змогла б самостійно переміщатися по відношенню до решти ферми.

Два однакових горизонтальних стрижня. Той, що вище має сили натягу однакової величини, що діють на кожен кінець, кожен вектор сили спрямований далеко від середини стрижня. Наведений нижче має сили стиснення однакової величини, що діють на кожен кінець, кожен вектор сили спрямований на середину стрижня. — Малюнок $\PageIndex{1}$ : Ферми виготовляються повністю з двосилових елементів. Це означає, що кожен член буде або в напрузі, або стисненні, як показано тут.

Ферми можуть бути розбиті далі на плоскі ферми і космічні ферми. Плоска ферма - це ферма, де всі елементи лежать в одній площині. Це означає, що плоскі ферми по суті можна розглядати як двовимірні системи. Космічні ферми, з іншого боку, мають елементи, які не обмежуються однією площиною. Це означає, що космічні ферми потрібно аналізувати як тривимірну систему.

Ферма даху з з'єднаних дерев'яних балок, які всі лежать в одній площині, поруч з будинком, що будується в засніженому полі. — Малюнок $\PageIndex{2}$ : Всі члени цих ферм лежать в одній площині. Ці кроквяні ферми є прикладом плоского кроквяної ферми. Зображення за допомогою CC-BY-SA 3.0.

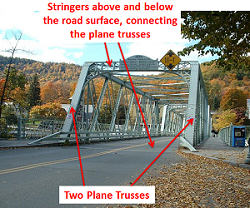
Металевий кроквяний міст, що містить асфальтовану проїжджу частину. Мітка вказує на те, що сторони моста є площинними фермами, а інша мітка вказує стрингери у верхній частині сторін моста та під дорожнім покриттям як з'єднувальні плоскі ферми. — Малюнок $\PageIndex{3}$ : Цей міст складається з двох плоских ферм, з'єднаних членами, званими стрингерами. Адаптовано з зображення ToddC4176 CC-BY-SA 3.0.

Глядацька зала зі стелею, що складається з квадратних плиток, кожен ряд підтримується мережею металевих ферм, які утворюють трикутні призми, основа яких утворена плитками. — Малюнок $\PageIndex{4}$ : Ця несуча кроквяна ферма даху не лежить в одній площині. Це приклад космічної ферми. Зображення за допомогою IM3847 CC-BY-SA 4.0.

Металева лінія електропередач вежа в засніженому полі. — Малюнок $\PageIndex{5}$ : Вежа лінії електропередач також не лежить в одній площині і тому є космічною фермою. Зображення Андерса Лагероса CC-BY-SA 2.5.

Аналіз ферм:

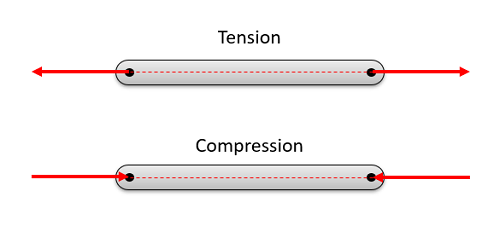
Коли ми говоримо про аналіз ферми, ми зазвичай шукаємо, щоб виявити не тільки зовнішні сили, що діють на кроквяну конструкцію, але і сили, що діють на кожен елемент всередині ферми. Оскільки кожен елемент ферми є двома силовими елементами, нам просто потрібно визначити величину сили на кожному елементі та визначити, чи є кожен елемент у напрузі чи стисненні.

Щоб визначити ці невідомі, у нас є два методи: метод стиків, і метод перетинів. Обидва дадуть однакові результати, але кожен через різний процес.

Метод з'єднань фокусується на стиках, або точках з'єднання, де члени збираються разом. Ми припускаємо, що у нас є штифт в кожній з цих точок, які ми моделюємо як частинки, ми малюємо діаграму вільного тіла для кожного штифта, а потім ми виписуємо рівняння рівноваги для кожного штифта. Це призведе до великої кількості рівнянь рівноваги, які ми можемо використовувати для вирішення великої кількості невідомих сил.

Метод секцій передбачає прикидання розщеплення ферми на дві або більше різних секцій, а потім аналіз кожної секції як окремого жорсткого тіла в рівновазі. У цьому методі визначаємо відповідні розділи, малюємо вільні діаграми тіла для кожного розділу, а потім виписуємо рівняння рівноваги для кожного розділу.

Метод з'єднань зазвичай є найпростішим і швидким методом для вирішення всіх невідомих сил в фермі. Метод секцій, з іншого боку, краще підходить для націлювання та вирішення сил лише за кілька членів без необхідності вирішувати всі невідомі. Крім того, ці методи можна комбінувати, якщо це необхідно, щоб найкращим чином відповідати цілям вирішувача проблем.