2.4: Діелектрична сприйнятливість

Якщо поле інциденту моночасте, тобто

$$\vec{E} (t)^{(+)} = \hat{\vec{E}} e^{i\omega t},\label{eq2.4.1}$$

і якщо припустити, що$w$ інверсія атома буде добре представлена його середнім за часом$w_s$, то дипольний момент буде коливатися з такою ж частотою в стаціонарному стані

$$d = \hat{d} e^{i\omega t},\label{eq2.4.2}$$

і інверсія буде підлаштовуватися під нове стаціонарне значення$w_s$. З ансац ($\ref{eq2.4.1}$) і ($\ref{eq2.4.2}$) в Eqs. (2.3.98) і (2.3.99), отримуємо

$$\hat{d} = \dfrac{-j}{2\hbar} \dfrac{w_s}{1/T_2 + j(\omega - \omega_{eg})} \vec{M} \hat{\vec{E}},\label{eq2.4.3}$$

$$w_s = \dfrac{w_0}{1 + \tfrac{T_1}{\hbar^2} \tfrac{1/T_2 |\vec{M} \hat{\vec{E}}|^2}{(1/T_2)^2 + (\omega_{eg} - \omega)^2}}. \nonumber$$

Введемо нормалізовану функцію лінійної форми, яка в даному випадку є Лоренціаном,

$$L(\omega) = \dfrac{(1/T_2)^2}{(1/T_2)^2 + (\omega_{eg} - \omega)^2}, \nonumber$$

і з'єднати квадрат поля$|\hat{\vec{E}}|^2$ з напруженістю$I$ поширюється плоской хвилі, згідно з рівнянням (2.2.27)$I = \dfrac{1}{2Z_F} |\hat{\vec{E}}|^2$,

$$w_s = \dfrac{w_0}{1 + \tfrac{I}{I_s} L(\omega)}. \nonumber$$

При цьому стаціонарна інверсія залежить від інтенсивності падаючого світла, тому$w_0$ може називатися ненасиченою інверсією,$w_s$ насиченою інверсією і$I_s$, при

$$I_s = \left [ \dfrac{2T_1T_2 Z_F}{\hbar^2} \dfrac{|\vec{M} \hat{\vec{E}}|^2}{|\hat{\vec{E}}|^2} \right ]^{-1}, \nonumber$$

інтенсивність насичення. Тоді очікуване значення дипольного оператора задається

$$<\vec{p}>= -(\vec{M}^* d + \vec{M} d^*). \nonumber$$

Множення з числом атомів на одиницю об'єму$N$ пов'язує дипольний момент атома зі складною поляризацією$\hat{\vec{P}}^+$ середовища, а отже, і до сприйнятливості по

$$\hat{\vec{P}}^{(+)} = -2N \vec{M}^* \hat{d},\label{eq2.4.9}$$

$$\hat{\vec{P}}^{(+)} = \epsilon_x \chi (\omega) \hat{\vec{E}}.\label{eq2.4.10}$$

З визначень ($\ref{eq2.4.9}$), ($\ref{eq2.4.10}$) і Рівняння ($\ref{eq2.4.2}$) отримано для лінійної сприйнятливості середовища

$$\chi (\omega) = \vec{M}^* \vec{M}^T \dfrac{jN}{\hbar \epsilon_0} \dfrac{w_s}{1/T_2 + j(\omega - \omega_{eg})}. \nonumber$$

який є тензором. Далі ми припускаємо, що напрямок атома є випадковим, тобто вирівнювання атомного дипольного моменту$\vec{M}$ і електричного поля є випадковим. Тому ми повинні усереднити за кутом, укладеним між електричним полем хвилі та атомним дипольним моментом, що призводить до

$$\overline{\left (\begin{matrix} M_x M_x & M_x M_y & M_x M_z \\ M_y M_x & M_y M_y & M_y M_z \\ M_z M_x & M_z M_y & M_z M_z \end{matrix} \right )} = \left (\begin{matrix} \overline{M_x^2} & 0 & 0 \\ 0 & \overline{M_y^2} & 0 \\ 0 & 0 & \overline{M_y^2} \end{matrix} \right ) = \dfrac{1}{3} |\vec{M}|^2 1. \nonumber$$

Таким чином, для однорідних та ізотропних середовищ тензор сприйнятливості зменшується до скалярного.

$$\chi (\omega) = \dfrac{1}{3} |\vec{M}|^2 \dfrac{jN}{\hbar \epsilon_0} \dfrac{w_s}{1/T_2 + j (\omega - \omega_{eg})}. \nonumber$$

Реальна і уявна частина сприйнятливості

$$\chi (\omega) = \chi ' (\omega) + j \chi '' (\omega) \nonumber$$

потім даються

$$\chi '(\omega) = -\dfrac{|\vec{M}|^2 N w_s T_2^2 (\omega_{eg} - \omega)}{3\hbar \epsilon_0} L(\omega), \nonumber$$

$$\chi '' (\omega) = \dfrac{|\vec{M}|^2 N w_s T_s}{3 \hbar \epsilon_0} L(\omega). \nonumber$$

Якщо падаюче випромінювання досить слабке, тобто

$$T_1 T_2 \dfrac{|\vec{M}^* \hat{\vec{E}}|^2}{\hbar^2} L(\omega) \ll 1 \nonumber$$

отримуємо$w_s \approx w_0$. Оскільки$w_0 < 0$, а особливо для оптичних переходів$w_0 = -1$, реальна і уявна частина сприйнятливості показані на малюнку 2.4.

Малюнок 2.4: Реальна і уявна частина комплексної сприйнятливості.

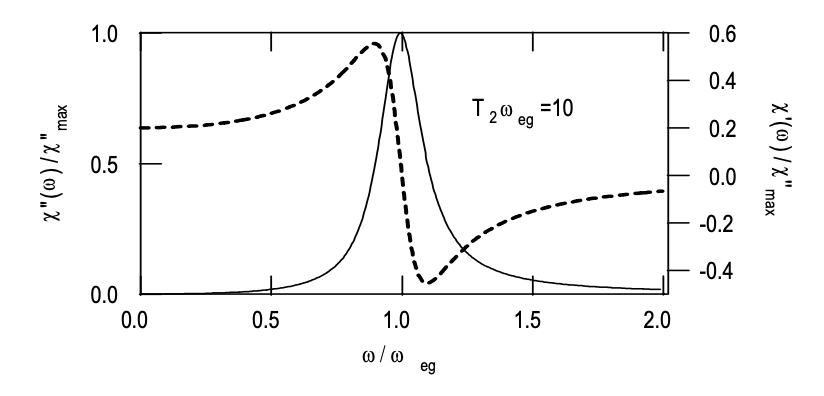
Обчислена квантова сприйнятливість добре порівнюється з класичною сприйнятливістю, отриманою з моделі гармонічного осцилятора, близької до частоти переходу для переходу з досить високою$Q = T_2\omega_{ab}$. Відзначимо, є помітне відхилення далеко від резонансу. Далекий резонанс наближення обертової хвилі не слід використовувати.

Фізичний сенс реальної і уявної частини сприйнятливості стає очевидним, коли розглядається поширення плоской електромагнітної хвилі через це середовище,

$$\vec{E} (z, t) = \Re \{ \hat{\vec{E}} e^{j(\omega t - kz)} \}, \nonumber$$

яка поширюється в$z$ позитивному напрямку. Константа поширення$k$ пов'язана з сприйнятливістю

$$k = \omega \sqrt{\mu_0 \epsilon_0 (1 + \chi (\omega))} \approx k_0 \left (1 + \dfrac{1}{2} \chi (\omega) \right ), \text{ with } k_0 = \omega \sqrt{\mu_0 \epsilon_0} \nonumber$$

для$|\chi| \ll 1$. За цим припущенням отримуємо

$$k = k_0 (1 + \dfrac{\chi '}{2} ) + j k_0 \dfrac{\chi ''}{2}. \nonumber$$

Реальна частина сприйнятливості сприяє показнику заломлення$n = 1 + \chi '/2$. У разі$\chi '' < 0$, уявна частина призводить до експоненціального загасання хвилі. Для$\chi '' > 0$ посилення має місце. Посилення хвилі можливо для$w_0 > 0$, тобто перевернутої середовища.

Швидкість$1/T_2$ фазової релаксації дипольного моменту визначає ширину лінії поглинання або смугу пропускання підсилювача.