2.3: Рівняння Блоха
- Page ID
- 32091
Атоми з низькою концентрацією показують лінійні спектри, виявлені в газових, барвникових та деяких твердотільних лазерних середовищах. Зазвичай в атомному, молекулярному або твердотільному середовищі існує нескінченно багато власних енергетичних станів і спектральні лінії пов'язані з дозволеними переходами між двома цими енергетичними власними станами. Для багатьох фізичних міркувань вже достатньо взяти до уваги лише два можливі власні енергетичні стани, наприклад ті, які пов'язані з лазерним переходом. Накачування лазера може бути описана феноменологічними релаксаційними процесами в верхній лазерний рівень і поза нижнім лазерним рівнем. Отриману просту модель часто називають дворівневим атомом, який математично також еквівалентний частинці спіна 1/2 у зовнішньому магнітному полі, оскільки спін може бути лише паралельним або анти- паралельним полю, тобто має два енергетичні рівні і енергетичні власні стани. Взаємодія дворівневого атома або спина з електричним або магнітним полем описується рівняннями Блоха.
Дворівнева модель
Атом, що має лише два власні значення енергії, описується двовимірним простором станів, що охоплюються двома власними енергетичними станами |\(e\)\ rangle і |\(g\)\ rangle. Ці два стани складають повну ортонормальну систему. Відповідними енергетичними власними значеннями є\(E_e\) і\(E_g\) (рис. 2.2).

У положенні-, тобто x-представленні, ці стани відповідають хвильовим функціям
\[\psi_e(x) = \langle x|e \rangle , \ \ \ \ \ \text{ and } \psi_g(x) = \langle x|g \rangle .\label{eq2.3.1} \]
Гамільтоніан атома задається
\[H_A = E_e |e\rangle \langle e| + E_g |g\rangle \langle g|. \nonumber \]
У цьому двовимірному просторі станів можливі лише\(2 \times 2 = 4\) лінійно незалежні лінійні оператори. Можливий вибір для операторської бази в цьому просторі
\[1 = |e \rangle \langle e| + |g\rangle \langle g|, \nonumber \]
\[\sigma_z = |e\rangle \langle e| - |g\rangle \langle g|,\label{eq2.3.4} \]
\[\sigma^+ = |e\rangle \langle g|, \nonumber \]
\[\sigma^- = |g\rangle \langle e|.\label{eq2.3.6} \]
Неермітівські оператори\(\sigma^{\pm}\) можуть бути замінені ермітовими операторами\(\sigma_{x,y}\)
\[\sigma_x = \sigma^+ + \sigma^-, \nonumber \]
\[\sigma_y = -j\sigma^+ + j\sigma^-. \nonumber \]
Фізичний сенс цих операторів стає очевидним, якщо дивитися на дію при застосуванні до довільного стану.
\[|\psi \rangle = c_g |g \rangle + c_e| e\rangle .\label{eq2.3.9} \]
Отримуємо
\[\sigma^+|\psi \rangle = c_g|e\rangle , \nonumber \]
\[\sigma^-|\psi \rangle = c_e|g\rangle , \nonumber \]
\[\sigma_z|\psi \rangle = c_e|e\rangle -c_g |g\rangle . \nonumber \]
Оператор\(\sigma^+\) генерує перехід від землі до збудженого стану, а\(\sigma^-\) робить зворотне. На відміну від\(\sigma^+\) і\(\sigma^-\),\(\sigma_z\) є ермітовим оператором, а його очікуване значення - це спостережувана фізична величина з очікуваним значенням
\[\langle \psi |\sigma_z| \psi \rangle = |c_e|^2 - |c_g|^2 = \omega, \nonumber \]
\(\omega\)інверсія атома, так як\(|c_e|^2\) і\(|c_g|^2\) є ймовірностями знаходження атома в стані\(|e \rangle \) або\(|g \rangle \) при відповідному вимірюванні.
Якщо розглядати ансамбль\(N\) атомів, загальна інверсія була б\(\sigma = N\langle \psi |\sigma_z| \psi \rangle \). Якщо відокремити від гамільтоніана (рівняння\(\ref{eq2.3.1}\)) член\((E_e + E_g)/2 \cdot 1\), де 1 позначає матрицю одиниці, відповідно перемасштабуємо енергетичні значення і отримаємо для гамільтоніана дворівневої системи
\[H_A = \dfrac{1}{2} \hat{h} \omega_{eg} \sigma_z, \nonumber \]
з частотою переходу
\[\omega_{eg} = \dfrac{1}{\hat{h}} (E_e - E_g). \nonumber \]
Ця форма гамільтоніана сприятлива. Існують наступні взаємозв'язки між операторами (Рівняння\(\ref{eq2.3.4}\)) до (Рівняння\(\ref{eq2.3.6}\))
\[[\sigma^+, \sigma^-] = \sigma_z,\label{eq2.3.16} \]
\[[\sigma^+, \sigma_z] = -2\sigma^+, \nonumber \]
\[[\sigma^-, \sigma_z] = 2\sigma^-,\label{eq2.3.18} \]
і антикомутаторські відносини відповідно
\[[\sigma^+, \sigma^-]_+ = 1, \nonumber \]
\[[\sigma^+, \sigma_z]_+ = 0, \nonumber \]
\[[\sigma^-, \sigma_z]_+ = 0, \nonumber \]
\[[\sigma^-, \sigma^-]_+ = [\sigma^+, \sigma^+]_+ = 0, \nonumber \]
\(\sigma_x\)Оператори\(\sigma_y\)\(\sigma_z\) виконують відносини комутатора моменту моменту
\[[\sigma_x, \sigma_y] = 2j \sigma_z, \nonumber \]
\[[\sigma_y, \sigma_z] = 2j \sigma_x, \nonumber \]
\[[\sigma_z, \sigma_x] = 2j \sigma_y, \nonumber \]
Двовимірний простір стану можна представити у вигляді векторів\(\mathbb{C}^2\) за правилом:
\[|\psi \rangle = c_e| e\rangle + c_g|g \rangle \to \ \ \left (\begin{matrix} c_e \\ c_g \end{matrix} \right ). \nonumber \]
Потім оператори представляються матрицями.
\[\sigma^+ \to \left ( \begin{matrix} 0 & 1 \\ 0 & 0 \end{matrix} \right ),\label{eq2.3.27} \]
\[\sigma^- \to \left ( \begin{matrix} 0 & 0 \\ 1 & 0 \end{matrix} \right ), \nonumber \]
\[\sigma_z \to \left ( \begin{matrix} 1 & 0 \\ 0 & -1 \end{matrix} \right ), \nonumber \]
\[1 \to \left ( \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right ).\label{eq.2.3.30} \]
Взаємодія атомного поля в дипольному наближенні
Дипольний момент атома по суті\(\tilde{P}\) визначається оператором положення\(\vec{x}\) за допомогою
\[\vec{P} = -e_0 \vec{x}.\label{eq2.3.31} \]
Тоді очікуване значення для дипольного моменту атома в стані (Рівняння\(\ref{eq2.3.9}\)) дорівнює
\[\begin{array} {rcl} {\langle \psi |\vec{P}|\psi \rangle } & = & {-e_0 (|c_e|^2 \langle e|\bar{x}|e \rangle + c_e c_g^* \langle g|\bar{x}| e\rangle } \\ {} & + & {c_gc_e^* \langle e|\bar{x}| g\rangle +|c_g|^2 \langle g|\bar{x}|g \rangle ).}\end{array} \nonumber \]
Для простоти можна припустити, що середовищем є атомний газ. Атоми мають інверсійну симетрію, тому власні енергетичні стани повинні бути симетричними або антисиметричними, тобто\(\langle e|\bar{x}|e\rangle =\langle g|\bar{x}|g\rangle =0\). Отримуємо
\[\langle \psi |\bar{P} \psi\rangle = -e_0 (c_ec_g^* \langle g|\bar{x}|e\rangle + c_g c_e^* \langle g|\bar{x}|e\rangle ^*). \nonumber \]
(Зверніть увагу, це означає, що в атомі немає постійного дипольного моменту, який знаходиться в енергетичному власному стані. Зверніть увагу, що це може бути не так у твердому вигляді. Атоми, що складають тверде тіло, орієнтовані в решітку, яка може порушити симетрію. Якщо так, то є постійні дипольні моменти і, отже, елементи матриці\(\langle e|\bar{x}|e \rangle \) і не\(\langle g|\bar{x}|g \rangle \) зникнуть. Якщо так, є також кришталеві поля, які потім передбачають зсув рівня, за допомогою лінійного ефекту Старка.) Таким чином, атом проявляє лише дипольний момент в середньому, якщо продукт\(c_ec_g^* \ne 0\), тобто стан атома знаходиться в суперпозиції станів\(|e \rangle \) і\(|g \rangle \).
З елементами дипольної матриці
\[\bar{M} = e_0 \langle g|\bar{x}|e\rangle \nonumber \]
очікуване значення для дипольного моменту можна записати як
\[\langle \psi |\bar{P}| \psi \rangle = -(c_e c_g^* \vec{M} + c_g c_e^* \vec{M}^*) = - \langle \psi |(\sigma^+ \vec{M}^* + \sigma^- \vec{M})|\psi \rangle . \nonumber \]
Оскільки це вірно для довільного стану, дипольний оператор (Equation\(\ref{eq2.3.31}\)) представлений
\[\vec{P} = \vec{P}^+ + \vec{P}^- = -\vec{M}^* \sigma^+ - \vec{M} \sigma^-.\label{eq2.3.36} \]
Тому оператори\(\sigma^+\) і\(\sigma^-\) пропорційні комплексним операторам дипольних моментів\(\vec{P}^+\) і\(\vec{P}^-\), відповідно.
Енергія електричного диполя в електричному полі дорівнює
\[H_{A - F} = -\vec{P} \cdot \vec{E} (\vec{x}_A, t). \nonumber \]
Електричне поле в положенні атома,\(\vec{x}_A\), може бути записано як
\[\vec{E} (\vec{x}_A, t) = \dfrac{1}{2} \left (\vec{E} (t)^{(+)} + \vec{E} (t)^{(-)} \right ) =\dfrac{1}{2} \left (\hat{\vec{E}} (t)^{(+)} e^{j\omega t} + \hat{\vec{E}} (t)^{(-)} e^{-j\omega t}\right ), \nonumber \]
де\(\hat{\vec{E}} (t)^{(+)}\) позначає повільно змінюється складну оболонку поля с\(\omega \approx \omega_{eg}\). У наближенні обертової хвилі (RWA) ми зберігаємо лише повільно змінювані компоненти у взаємодії гамільтоніана. Як ми побачимо пізніше, якщо немає поля, оператор\(\sigma^+\) розвивається подібно\(\sigma^+ (t) = \sigma^+ (0) e^{j \omega_{eg} t}\), таким чином ми отримуємо в RWA
\[H_{A-F} = -\vec{P} \cdot \vec{E} (\vec{x}_A, t) \approx \nonumber \]
\[\approx H_{A-F}^{RWA} =\dfrac{1}{2} \vec{M}^* \vec{E} (t)^{(-)} \sigma^+ + h.c.. \nonumber \]
Рівняння Шредінгера для дворівневого атома в класичному полі задається
\[jh\dfrac{d}{dt} |\psi \rangle = (H_A + H_{A- F}|\psi \rangle \nonumber \]
\[\approx (H_A + H_{A - F}^{RWA})|\psi \rangle . \nonumber \]
Записуємо в енергетичному поданні, отримуємо
\[\dfrac{d}{dt} c_e = -j\dfrac{\omega_{eg}}{2} c_e - j \Omega_r e^{-j\omega t} c_g,\label{eq2.3.43} \]
\[\dfrac{d}{dt} c_g = +j\dfrac{\omega_{eg}}{2} c_g - j \Omega_r e^{+j\omega t} c_e,\label{eq2.3.44} \]
з RABI-частотою, визначеною як
\[\Omega_r = \dfrac{\vec{M}^* \hat{\vec{E}}}{2\hbar}. \nonumber \]
На даний момент ми припускаємо, що Rabi-частота реальна. Якщо це не так, для усунення цієї фази\(c_{a,b}\) буде необхідно перетворення, що включає зсув фаз в амплітудах. Як і очікувалося, поле з'єднує енергетичні власні стани.
Коливання Рабі
Якщо падаюче світло має постійну амплітуду поля\(\hat{\vec{E}}\) Eqs. (\(\ref{eq2.3.43}\)) і (\(\ref{eq2.3.44}\)) можна вирішити, і ми спостерігаємо коливання в різниці популяції, коливання Рабі [1]. Щоб показати це, введемо розстроювання між польовим і атомним резонансом.
\[\Delta = \dfrac{\omega_{ab} - \omega}{2} \nonumber \]
і нові амплітуди ймовірності
\[C_e = c_e e^{j \tfrac{\omega}{2} t}, \nonumber \]
\[C_g = c_g e^{-j \tfrac{\omega}{2} t}, \nonumber \]
Це призводить до появи нової системи рівнянь з постійними коефіцієнтами.
\[\dfrac{d}{dt} C_e = -j\Delta C_e - j \Omega_r C_g, \nonumber \]
\[\dfrac{d}{dt} C_g = +j\Delta C_g - j \Omega_r C_e, \nonumber \]
Зверніть увагу, це зв'язок рівнянь режиму в часі. Тепер режими - електронні замість фотонних. Але в іншому все те ж саме. У випадку зникнення розстроювання особливо легко усунути одну зі змінних, і ми приходимо до
\[\dfrac{d^2}{dt^2} C_e = -\Omega_r^2 C_e \nonumber \]
\[\dfrac{d^2}{dt^2} C_g = -\Omega_r^2 C_g \nonumber \]
Рішенням цієї множини рівнянь є коливання, які ми шукаємо. Якщо атом знаходиться в момент часу\(t = 0\) в наземному стані, тобто\(C_g (0) = 1\) і\(C_e (0) = 0\), відповідно, ми приходимо до
\[|c_b (t)|^2 = \cos^2 (\Omega, t) \nonumber \]
\[|c_a (t)|^2 = \sin^2 (\Omega, t) \nonumber \]
Тоді ймовірності знаходження атома в землі або збудженому стані
\[\langle \vec{P}\rangle = -\vec{M} c_e c_g^* + c.c. \nonumber \]
\[=-\vec{M} \sin (2\Omega_r t)\sin (\omega_{eg} t).\label{eq2.3.56} \]
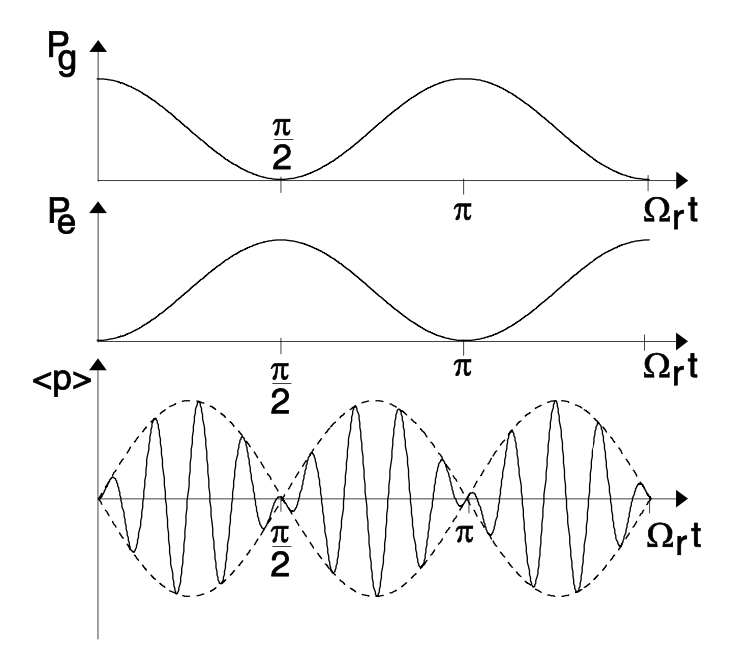
Когерентне зовнішнє поле рухає популяцію атомної системи між двома доступними станами з періодом\(T_r = \pi/\Omega_r\). Застосування поля лише протягом половини цього періоду призводить до повної інверсії популяції. Ці коливання рабі спостерігалися в різних системах, починаючи від газів і закінчуючи напівпровідниками. Цікаво, що світло, що випромінюється від когерентно керованого дворівневого атома, за частотою не ідентичний рушійному полю. Якщо ми подивимося на спектр Фур'є поляризації відповідно до Eq. (\(\ref{eq2.3.56}\)), отримуємо лінії на частотах\(\omega_{\pm} = \omega_{eg} \pm 2 \Omega_r\). Це явно нелінійний вихід, а бічні смуги називаються Mollow-Sidebands [2]. Найважливішим для існування цих коливань є когерентність атомної системи над хоча б одним Rabi-коливанням. Якщо ця когерентність руйнується досить швидко, коливання рабі не можуть відбутися, і тоді неможливо генерувати інверсію в дворівневій системі шляхом взаємодії зі світлом. Це стосується великого класу ситуацій у взаємодії світло-матерії. Тому нас цікавить, що відбувається в разі втрати когерентності внаслідок додаткової взаємодії атомів з тепловою ванною.
Оператор щільності
Для вивчення некогерентних або дисипативних процесів доцільно перейти до sta- статичного опису за допомогою оператора густини замість детермінованих хвильових функцій, аналогічних класичній статистичній механіці, де детерміновані траєкторії частинок замінюються розподілами ймовірностей.
Оператор щільності чистого стану визначається діадичним добутком стану з самим собою
\[\rho = |\psi \rangle \langle \psi| \nonumber \]
або у координатному представленні за допомогою\(2 \times 2\) −матриці
\[\rho = \left ( \begin{matrix} \rho_{ee} & \rho_{eg} \\ \rho_{ge} & \rho_{gg} \end{matrix} \right ). \nonumber \]
У разі чистого стану (\(\ref{eq2.3.9}\)) це
\[\rho = \left ( \begin{matrix} c_ec_e^* & c_ec_g^* \\ c_gc_e^* & c_gc_g^* \end{matrix} \right ). \nonumber \]
Очевидно, що для досить простого випадку дворівневої системи кожному елементу матриці щільності відповідає фізична величина. Основна діагональ містить ймовірності популяції для рівнів, а позадіагональним елементом є очікуване значення позитивної або негативної частотної складової дипольного моменту атома, тобто його внесок у середню поляризацію.
Очікуване значення довільного оператора\(A\) можна обчислити за допомогою формули трасування
\[\langle A \rangle = Tr\{\rho A\} =\langle \psi |A| \psi \rangle . \nonumber \]
Перевага оператора щільності полягає в тому, що суміші чистих станів також можуть розглядатися в статистичному сенсі. Наприклад, якщо атом знаходиться в стані\(|e \rangle \) з ймовірністю\(p_e\) і в стані\(|g \rangle \) з ймовірністю\(p_g\), оператор щільності
\[\rho = p_e|e\rangle \langle e|+p_g|g\rangle \langle g| \nonumber \]
визначено, які можуть бути використані для обчислення середніх значень спостережуваних у належному статистичному сенсі
\[\langle A\rangle =T_r \{\rho A\} = p_e\langle e|A|e\rangle +p_g \langle g|A|g\rangle . \nonumber \]
Оскільки матриці (\(\ref{eq2.3.27}\)) to (\(\ref{eq2.3.30}\)) будують повну базу у просторі\(2 \times 2\) −матриць, ми можемо висловити матрицю щільності як
\[\rho = \rho_{ee} \dfrac{1}{2} (1 + \sigma_z) + \rho_{gg} \dfrac{1}{2} (1 - \sigma_z) + \rho_{eg} \sigma^+ + \rho_{ge} \sigma^- \nonumber \]
\[=\dfrac{1}{2} 1 + \dfrac{1}{2} (\rho_{ee} -\rho_{gg}) \sigma_z + \rho_{eg} \sigma^+ + \rho_{ge} \sigma^-, \nonumber \]
так як слід матриці щільності завжди один (нормалізація). Вибираючи нову базу\(1, \sigma_x, \sigma_y, \sigma_z\), отримуємо
\[\rho = \dfrac{1}{2} 1 + \dfrac{1}{2} (\rho_{ee} - \rho_{gg})\sigma_z + d_x \sigma_x + d_y \sigma_y, \nonumber \]
із
\[d_x = \dfrac{1}{2} (\rho_{eg} + \rho_{ge}) = \Re\{\langle \sigma^{(+)} \rangle \}, \nonumber \]
\[d_y = \dfrac{j}{2} (\rho_{eg} - \rho_{ge}) = \Im\{\langle \sigma^{(+)} \rangle \}, \nonumber \]
Очікуване значення дипольного оператора задається (\(\ref{eq2.3.36}\))
\[\langle \vec{P}\rangle =T_r \{\rho \vec{P}\} = -\vec{M}^* Tr\{\rho \sigma^+\} + c.c. = -\vec{M}^* \rho_{ge} + c.c. \nonumber \]
З рівняння Шредінгера для хвильової функції\(|\psi \rangle \) ми можемо легко вивести рівняння руху для оператора густини, яке називається рівнянням фон Неймана
\[\dot{\rho} = \dfrac{d}{dt} |\psi \rangle \langle \psi| + h.c. = \dfrac{1}{j\hbar} H|\psi \rangle \langle \psi| - \dfrac{1}{j\hbar} |\psi \rangle \langle \psi| H = \dfrac{1}{j\hbar} [H, \rho]. \nonumber \]
Через лінійну природу рівняння це також правильне рівняння для оператора щільності, що описує довільну суміш станів. У випадку дворівневого атома рівняння фон Неймана дорівнює
\[\dot{\rho} = \dfrac{1}{j\hbar} [H_A, \rho] = -j \dfrac{\omega_{\in g}}{2} [\sigma_z, \rho]. \nonumber \]
Використовуючи комутаторні відносини (\(\ref{eq2.3.16}\)\(\ref{eq2.3.18}\)) - (), результат
\[\dot{\rho}_{\in e} = 0,\label{eq2.3.71} \]
\[\dot{\rho}_{gg} = 0, \nonumber \]
\[\dot{\rho}_{eg} = -j \omega_{eg} \rho_{eg} \to \rho_{eg} (t) = e^{-j \omega_{eg} t} \rho_{eg} (0), \nonumber \]
\[\dot{\rho}_{ge} = j \omega_{eg} \rho_{ge} \to \rho_{ge} (t) = e^{j \omega_{eg} t} \rho_{ge} (0).\label{eq2.3.74} \]
Знову ізольований дворівневий атом має досить просту динаміку, популяції постійні, тільки дипольний момент коливається з частотою переходу\(\omega_{\in g}\), якщо був індукований дипольний момент\(t = 0\), тобто система знаходиться в стані суперпозиції.
Енерго- і фазово-релаксація
В реальності ізольованого атома немає. Адже в нашому випадку нас цікавить випромінюючий атом, тобто він має дипольну взаємодію з полем. Зв'язка з нескінченно багатьма режимами вільного поля призводить вже до мимовільного випромінювання, незворотного процесу. Ми могли б лікувати цей процес, використовуючи гамільтоніан
\[H = H_A + H_F + H_{A-F}. \nonumber \]
Тут\(H_A\) знаходиться гамільтоніан атома, HF вільного поля і\(H_{A-F}\) описує взаємодію між ними. Повне лікування за цими напрямками виходить за рамки цього класу і зазвичай проводиться на заняттях з квантової механіки. Але результат цього розрахунку простий і виводить в рівняння фон Неймана матриці зниженої щільності, тобто матриці щільності атома. При швидкості спонтанної емісії\(1/\tau_{sp}\), тобто зворотному спонтанному часу життя\(\tau_{sp}\), популяції змінюються відповідно до
\[\dfrac{d}{dt} |c_e (t)|^2 = \dfrac{d}{dt} \rho_{ee} = -\Gamma_e \rho_{ee} + \Gamma_a \rho_{gg} \nonumber \]
з скороченнями
\[\Gamma_e = \dfrac{1}{\tau_{sp}} (n_{th} + 1), \nonumber \]
\[\Gamma_a = \dfrac{1}{\tau_{sp}} n_{th}.\label{eq2.3.78} \]
Тут\(n_{th}\) наведено кількість термічно збуджених фотонів в режимах вільного поля з частотою\(\omega_{eg}\)\(n_{th} = 1/(\exp (h\omega_{eg} /kT) - 1)\), при температурі\(T\).
Повна ймовірність перебувати в збудженому або наземному стані повинна підтримуватися, тобто
\[\dfrac{d}{dt} \rho_{gg} = -\dfrac{d}{dt} \rho_{ee} = \Gamma_e \rho_{ee} - \Gamma_a \rho_{gg}.\label{eq2.3.79} \]
Якщо популяції розпадаються, так само поляризація теж, так як\(\rho_{ge} = c_e^* c_g\), тобто
\[\dfrac{d}{dt} \rho_{ge} j \omega_{eg} \rho_{eg} - \dfrac{\Gamma_e + \Gamma_a}{2} \rho_{ge}.\label{eq2.3.80} \]
Таким чином, поглинання, а також процеси емісії також руйнівні для фази, отже, відповідні швидкості складаються в швидкості розпаду фази.
Враховуючи когерентні (\(\ref{eq2.3.71}\)-\(\ref{eq2.3.74}\)) та некогерентні процеси (\(\ref{eq2.3.79}\)-\(\ref{eq2.3.80}\)), отримані наступні рівняння для нормованого середнього дипольного моменту\(d = d_x + jd_y\) та інверсії\(w\)
\[\dot{d} = \dot{\rho}_{ge} = (j \omega_{eg} - \dfrac{1}{T_2})d,\label{eq2.3.81} \]
\[\dot{\omega} = \dot{\rho}_{ee} - \dot{\rho}_{gg} = \dfrac{\omega - \omega_0}{T_1},\label{eq2.3.82} \]
з постійними часом
\[\dfrac{1}{T_1} = \dfrac{2}{T_2} = \Gamma_e + \Gamma_a = \dfrac{2n_{th} + 1}{\tau_{sp}} \nonumber \]
і інверсія рівноваги\(w_0\), обумовлена тепловим збудженням атома тепловим полем
\[w_0 = \dfrac{\Gamma_a - \Gamma_e}{\Gamma_a + \Gamma_e} = \dfrac{-1}{1 + 2n_{th}} = -\tanh \left (\dfrac{\hbar\omega_{eg}}{2kT} \right ).\label{eq2.3.84} \]
Постійна часу\(T_1\) позначає енергетичну релаксацію в дворівневій системі і\(T_2\) фазову релаксацію. \(T_2\)час кореляції між амплітудами\(c_e\) і\(c_g\). Ця узгодженість руйнується при взаємодії дворівневої системи з навколишнім середовищем. У цій моделі енергетична релаксація становить половину фазової швидкості релаксації або
\[T_2 = 2T_1 \nonumber \]
Атоми в лазерному середовищі не тільки взаємодіють з електромагнітним полем, але крім того і з фононами решітки господаря, вони можуть зіткнутися один з одним в газовому лазері і так далі. Всі ці процеси необхідно враховувати при визначенні енергетичної і фазової швидкості релаксації. Деякі з цих процесів лише руйнують фазу, але насправді не призводять до втрати енергії в системі. Тому ці процеси зменшуються,\(T_2\) але не мають ніякого впливу на\(T_1\). У реальних системах час фазової релаксації найчастіше набагато коротше, ніж удвічі більше часу енергетичної релаксації,
\[T_2 \le 2 T_1. \nonumber \]
Якщо інверсія відхиляється від значення рівноваги,\(w_0\) вона розслабляється назад в рівновагу з постійною часу\(T_1\). Рівняння (\(\ref{eq2.3.84}\)) показує, що для всіх температур\(T \rangle 0\) інверсія негативна, тобто нижній рівень сильніше заселений, ніж верхній рівень. Таким чином, при некогерентному інверсії теплового світла в дворівневій системі досягти неможливо. Інверсія може бути досягнута тільки накачуванням некогерентним світлом, якщо в верхній лазерний рівень буде більше рівнів і подальших процесів релаксації. Завдяки цим релаксаційним процесам швидкість\(\Gamma_a\) відхиляється від вираження рівноваги (\(\ref{eq2.3.78}\)), і її доводиться замінювати швидкістю насоса\(\Lambda\). Якщо швидкість насоса\(\Lambda\) перевищує\(\Gamma_e\), інверсія, відповідна Equation (\(\ref{eq2.3.84}\)), стає позитивною,
\[w_0 = \dfrac{\Lambda - \Gamma_e}{\Lambda + \Gamma_e}. \nonumber \]
Якщо ми допускаємо штучні негативні температури, ми отримуємо з\(T \langle 0\) для співвідношення швидкості релаксації
\[\dfrac{\Gamma_e}{\Gamma_a} = \dfrac{1+\bar{n}}{\bar{n}} = e^{\tfrac{\hbar \omega_{eg}}{kT}} \langle 1. \nonumber \]
Таким чином, накачування дворівневої системи відганяє систему далеко від теплової рівноваги, чого і доводиться очікувати.
Дворівневий атом з когерентним класичним зовнішнім полем
Якщо крім зв'язку із зовнішньою тепловою ванною, яка моделює спонтанний розпад, накачування та інші некогерентні процеси, когерентне зовнішнє поле, гамільтоніан повинен бути розширений дипольною взаємодією з цим полем,
\[H_E = -\vec{P} \vec{E} (\vec{x}_A, t). \nonumber \]
Знову використовуємо взаємодію гамільтоніана в RWA
\[H_E = \dfrac{1}{2} \vec{M}^* \vec{E} (t)^{(-)} \sigma^+ + h.c.. \nonumber \]
Це призводить в рівнянні фон Неймана до додаткового члена
\[\dot{\rho} |_E = \dfrac{1}{j\hbar} [H_E, \rho] \nonumber \]
\[= \dfrac{1}{2j\hbar} \vec{M}^* \vec{E} (t)^{(-)} [\sigma^+, \rho] + h.c. \nonumber \]
або
\[\rho{\rho}_{ee}|_E = \dfrac{1}{2j\hbar} \vec{E}^{(-)} \rho_{ge} + c.c., \nonumber \]
\[\rho{\rho}_{ge}|_E = \dfrac{1}{2j\hbar} \vec{E}^{(+)} (\rho_{ee} -\rho_{gg}), \nonumber \]
\[\rho{\rho}_{gg}|_E = -\dfrac{1}{2j\hbar} \vec{E}^{(-)} \rho_{ge} + c.c., \nonumber \]
Еволюція дипольного моменту і інверсія змінюється
\[\dot{d}|_E = \dot{\rho}_{ge}|_E = \dfrac{1}{2j\hbar} \vec{M} \vec{E}^{(+)} w, \nonumber \]
\[\dot{w}|_E = \dot{\rho}_{ee}|_E - \dot{\rho}_{gg}|_E = \dfrac{1}{j\hbar} (\vec{M}^* \vec{E}^{(-)} d^* - \vec{M} \vec{E}^{(+)} d). \nonumber \]
Таким чином, загальна динаміка дворівневої системи, включаючи процеси накачування і дефазування від Eqs. (\(\ref{eq2.3.81}\)) і (\(\ref{eq2.3.82}\)) задається
\[\dot{d} = -(\dfrac{1}{T_2} - j \omega_{eg})d + \dfrac{1}{2j \hbar} \vec{M} \vec{E}^{(+)} w, \nonumber \]
\[\dot{w} = -\dfrac{w-w_0}{T_1} + \dfrac{1}{j\hbar} (\vec{M}^* \vec{E}^{(-)} d - \vec{M} \vec{E}^{(+)} d^*). \nonumber \]
Ці рівняння називаються рівняннями Блоха. Вони описують динаміку атома, що взаємодіє з класичним електричним полем. Разом з Equation (2.2.2) вони будують рівняння Максвелла-Блоха.
