Skip to main content
LibreTexts - Ukrayinska

3.3: Лінійно-лінійні напруги

  1. Last updated
  2. Save as PDF
  • Page ID
    32777

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Збалансований трифазний набір напруг має чітко певний набір лінійно-лінійних напруг. Якщо лінійно-нейтральні напруги задаються (9 - 11), то лінійно-лінійні напруги складають:

    \[\ v_{a b}=v_{a}-v_{b}=\operatorname{Re}\left[\underline{V}\left(1-e^{-j \frac{2 \pi}{3}}\right) e^{j \omega t}\right]\label{21} \]

    \[\ v_{b c}=v_{b}-v_{c}=\operatorname{Re}\left[\underline{V}\left(e^{-j \frac{2 \pi}{3}}-e^{j \frac{2 \pi}{3}}\right) e^{j \omega t}\right]\label{22} \]

    \[\ v_{c a}=v_{c}-v_{a}=R e\left[\underline{V}\left(e^{j \frac{2 \pi}{3}}-1\right) e^{j \omega t}\right]\label{23} \]

    і вони зводять до:

    \[\ v_{a b}=\operatorname{Re}\left[\sqrt{3} \underline{V} e^{j \frac{\pi}{6}} e^{j \omega t}\right]\label{24} \]

    \[\ v_{b c}=R e\left[\sqrt{3} \underline{V} e^{-j \frac{\pi}{2}} e^{j \omega t}\right]\label{25} \]

    \[\ v_{c a}=\operatorname{Re}\left[\sqrt{3} \underline{V} e^{j \frac{5 \pi}{6}} e^{j \omega t}\right]\label{26} \]

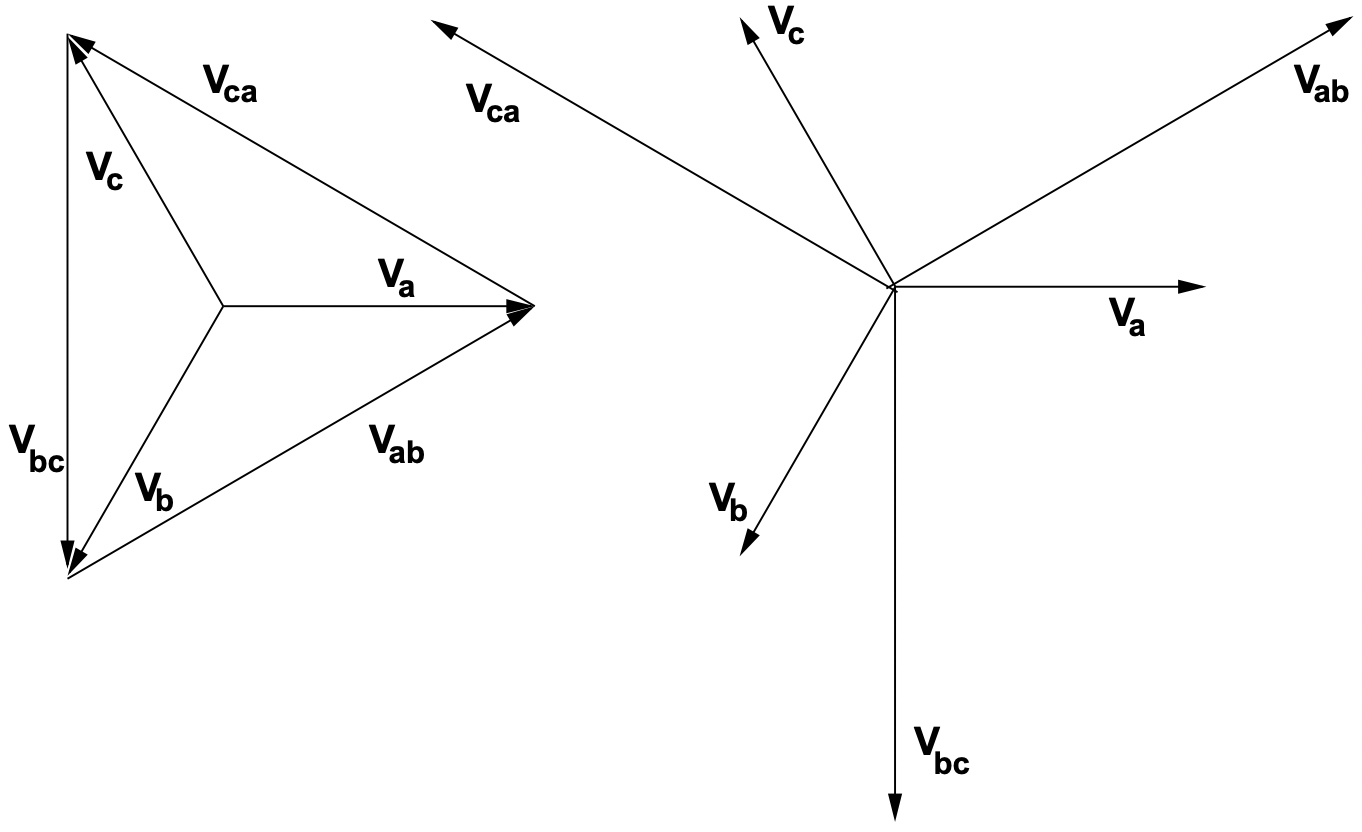
    Фазорна залежність напруг лінія-нейтраль і лінія-лінія показана на малюнку 8. Про цей зв'язок слід зазначити дві речі:

    • Набір напруги від лінії до лінії має величину, яка більша за напругу лінії-земля в рази\(\ \sqrt{3}\).
    • Лінійно-лінійні напруги зсуваються по фазі на 30 o попереду напруги лінія-нейтраль.

    Зрозуміло, що лінійні напруги самі по собі утворюють трифазний набір так само, як і напруги від лінії до нейтралі. Компоненти енергосистеми (джерела, обмотки трансформатора, навантаження і т.д.) можуть бути з'єднані як між лініями і нейтраллю, так і між лініями. Перше з'єднання часто називають wye, друге називається дельта, зі зрозумілих причин.

    Знімок екрана 2021-07-20 о 1.22.45 PM.pngМалюнок 8: Лінійно-нейтральні та лінійні напруги

    Слід зазначити, що з'єднання wye є принаймні потенційно з'єднанням з чотирма терміналами, тоді як дельта-з'єднання за своєю суттю є трьома терміналами. Різниця полягає в наявності нейтральної точки. При збалансованих умовах експлуатації це неважливо, але різниця очевидна і важлива в незбалансованих умовах.

    Приклад: Wye і Delta з'єднані навантаження

    Навантаження можуть бути підключені в конфігурації «лінія-нейтраль» або «лінія-лінія». Приклад використання такої гнучкості - в досить часто використовуваної розподільчої системі з напругою «лінія-нейтраль» 120 В, RMS. У цій системі напруга від лінії до лінії становить 208 В, RMS. Однофазні навантаження можуть бути підключені як лінія-лінія, так і лінія-нейтраль.

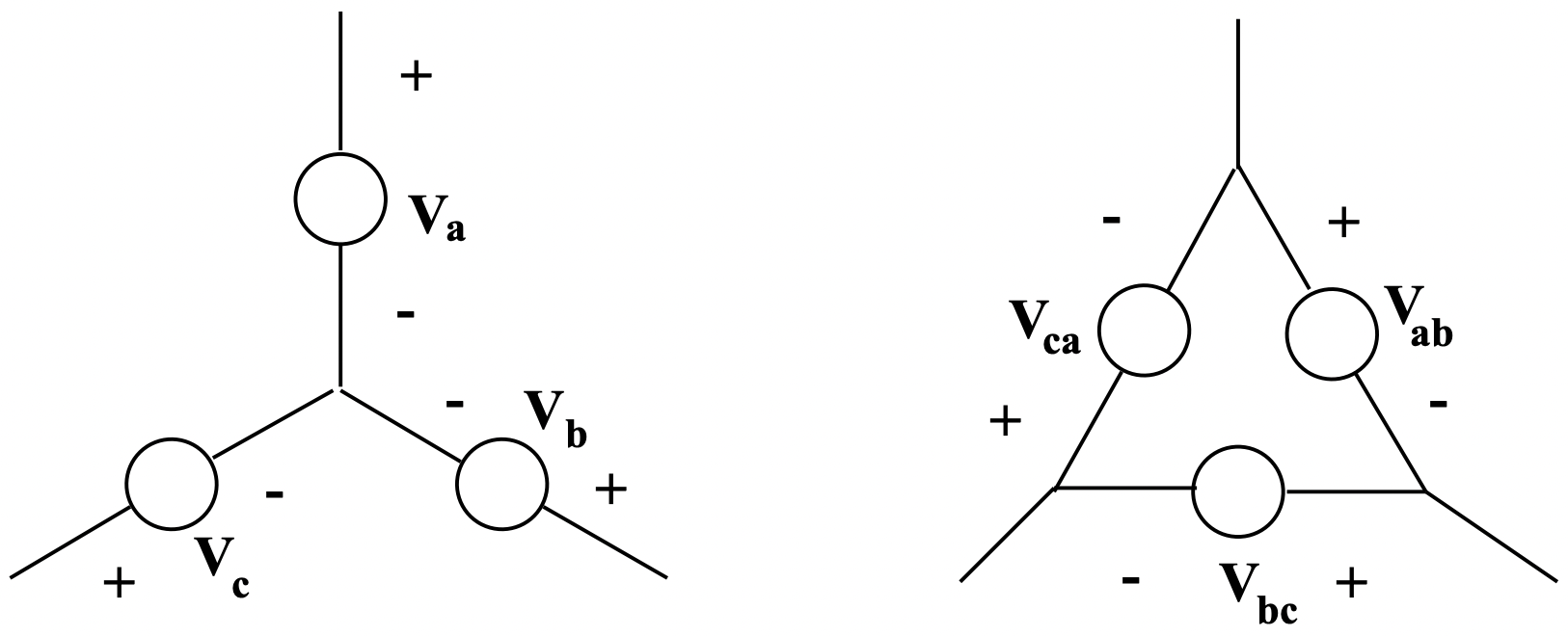    Знімок екрана 2021-07-20 в 1.25.33 PM.pngМалюнок 9: Wye і Delta підключені джерела напруги
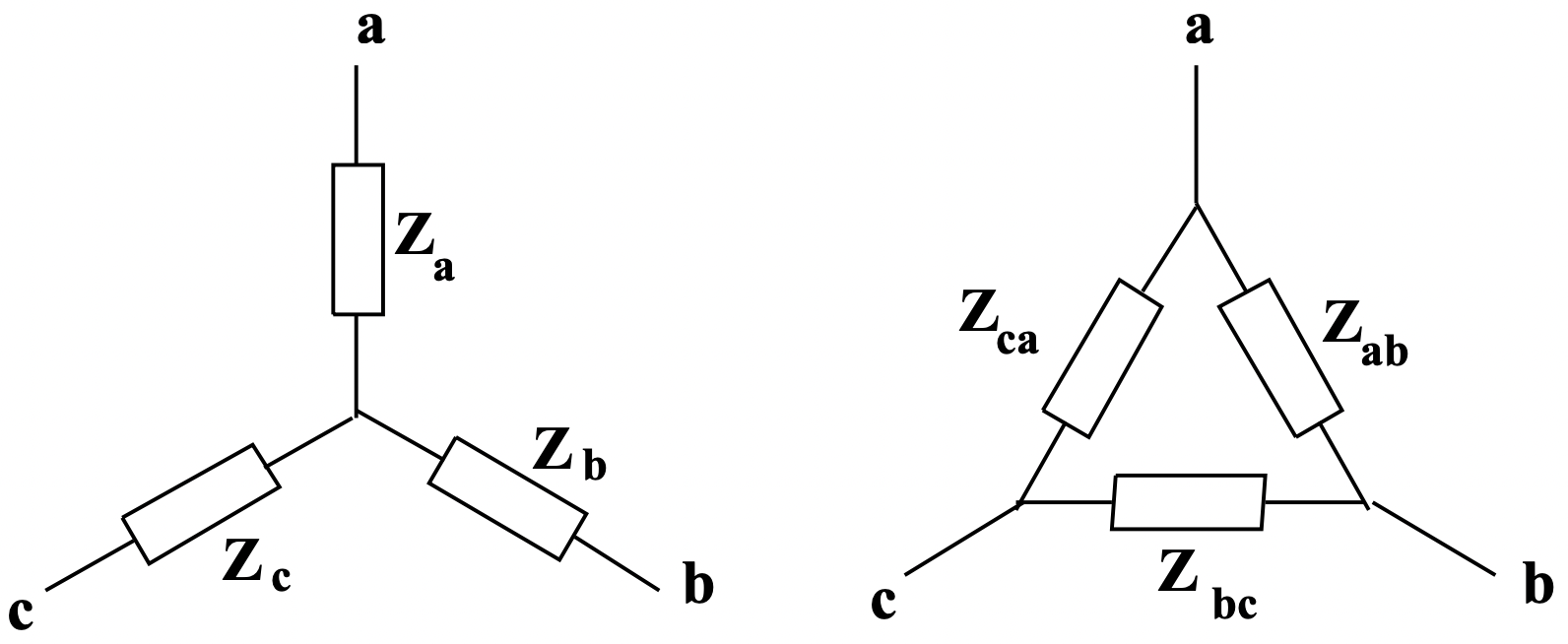    Знімок екрана 2021-07-20 в 1.26.20 PM.pngМалюнок 10: Wye та Delta з'єднані імпеданси

    Припустимо, необхідно спорудити резистивний нагрівач для подачі 6 кВт, який повинен бути виконаний з трьох елементів, які можуть бути з'єднані в будь-якому око або дельта. Кожен з трьох елементів повинен розсіювати 2000 Вт.

    Таким чином, оскільки\(\ P=\frac{V^{2}}{R}\), око підключених резисторів буде:

    \(\ R_{y}=\frac{120^{2}}{2000}=7.2 \Omega\)

    тоді як дельта підключених резисторів буде:

    \(\ R_{\Delta}=\frac{208^{2}}{2000}=21.6 \Omega\)

    Як пропонується в цьому прикладі, око і дельта з'єднані імпеданси часто безпосередньо еквівалентні. По суті, незаземлені з'єднання - це трьохклемні мережі, які можуть бути представлені двома способами. Дві мережі, показані на малюнку 10, комбінації трьох пасивних імпедансів, безпосередньо еквівалентні та однакові за своєю термінальною поведінкою, якщо відносини між елементами наведені в (27 - 32).

    \[\ \underline{Z}_{a b}=\frac{\underline{Z}_{a} \underline{Z}_{b}+\underline{Z}_{b} \underline{Z}_{c}+\underline{Z}_{c} \underline{Z}_{a}}{\underline{Z}_{c}}\label{27} \]

    \[\ \underline{Z}_{b c}=\frac{\underline{Z}_{a} \underline{Z}_{b}+\underline{Z}_{b} \underline{Z}_{c}+\underline{Z}_{c} \underline{Z}_{a}}{\underline{Z}_{a}}\label{28} \]

    \[\ \underline{Z}_{c a}=\frac{\underline{Z}_{a} \underline{Z}_{b}+\underline{Z}_{b} \underline{Z}_{c}+\underline{Z}_{c} \underline{Z}_{a}}{\underline{Z}_{b}}\label{29} \]

    \[\ \underline{Z}_{a}=\frac{\underline{Z}_{a b} \underline{Z}_{c a}}{\underline{Z}_{a b}+\underline{Z}_{b c}+\underline{Z}_{c a}}\label{30} \]

    \[\ \underline{Z}_{b}=\frac{\underline{Z}_{a b} \underline{Z}_{b c}}{\underline{Z}_{a b}+\underline{Z}_{b c}+\underline{Z}_{c a}}\label{31} \]

    \[\ \underline{Z}_{c}=\frac{\underline{Z}_{b c} \underline{Z}_{c a}}{\underline{Z}_{a b}+\underline{Z}_{b c}+\underline{Z}_{c a}}\label{32} \]

    Окремим випадком еквівалентності шлях-дельта є збалансовані навантаження, при яких:

    \(\ \underline{Z}_{a}=\underline{Z}_{b}=\underline{Z}_{c}=\underline{Z}_{y}\)

    і

    \(\ \underline{Z}_{a b}=\underline{Z}_{b c}=\underline{Z}_{c a}=\underline{Z}_{\Delta}\)

    в якому випадку:

    \(\ \underline{Z}_{\Delta}=3 \underline{Z}_{y}\)

    Приклад: Використання Wye-Delta для незбалансованих навантажень

    Незбалансована навантаження, показана на малюнку 11, підключається до збалансованого джерела напруги. Завдання полягає у визначенні струмів лінії. Зверніть увагу, що його навантаження незаземлена (якби вона була заземлена, це була б банальна проблема). Напруги задаються:

    \ (\\ begin {масив} {l}
    v_ {a} =V\ cos\ омега т\\
    v_ {b} =V\ cos\ лівий (\ омега т-\ frac {2\ pi} {3}\ праворуч)\\
    v_ {c} =V\ cos\ ліворуч (\ омега t+\ frac {2\ pi} {3}\ праворуч)\ кінець {масив}
    \ кінець {}\)

    Щоб вирішити цю проблему, перетворіть як джерело, так і навантаження в дельта-еквівалентні з'єднання, як показано на малюнку 12. Значення трьох резисторів такі:

    \ (\\ begin {масив} {c}
    r_ {a b} =r_ {c a} =\ frac {2+4+2} {2} =4\
    r_ {b c} =\ frac {2+4+2} {1} =8
    \ end {масив}\)

    Комплексними амплітудами еквівалентних джерел напруги є:

    \ (\\ begin {масив} {ll}
    \ підкреслення {V} _ {a b} &=\ підкреслення {V} _ {a} -\ підкреслення {V} _ {b} =\ підкреслення {V}\ вліво (1-e^ {-j\ frac {2\ pi} {3}}\ праворуч) &=\ підкреслення {V}\ sqrt {3}\ frac {\ pi} {6}}\
    \ підкреслення {V} _ {b c} &=\ підкреслення {V} _ {b} -\ підкреслення {V} _ {c} =\ підкреслення {V}\ ліворуч (e^ {-j\ frac {2\ пі} {3}} -e^ {j\ frac {2\ pi} {3}}\ право) &=\ підкреслення {V}\ sqrt {3} e^ {-j\ frac {\ pi} {2}}\
    \ підкреслення {V} _ {c a} &=\ підкреслення {V} _ {c} _ {c} -\ підкреслення {V} _ {a} =\ підкреслення {V}\ ліворуч (e^ {j\ frac {2\ pi} {3}} -1\ праворуч) &=\ підкреслення {V}\ sqrt {3} e^ {j\ frac {5\ pi} {6}}
    \ end {масив}\)

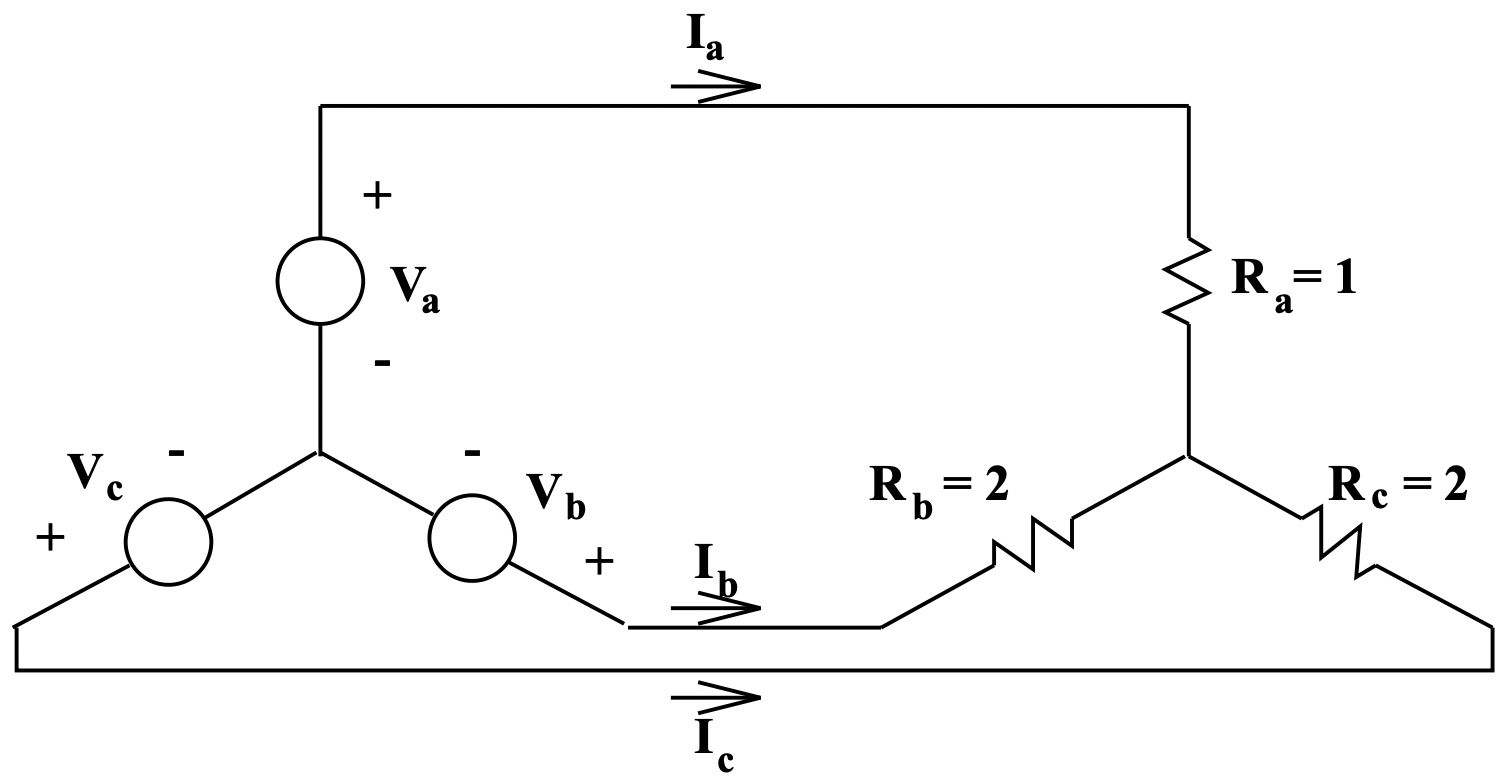    Знімок екрана 2021-07-20 в 1.44.27 PM.pngМалюнок 11: Незбалансоване навантаження
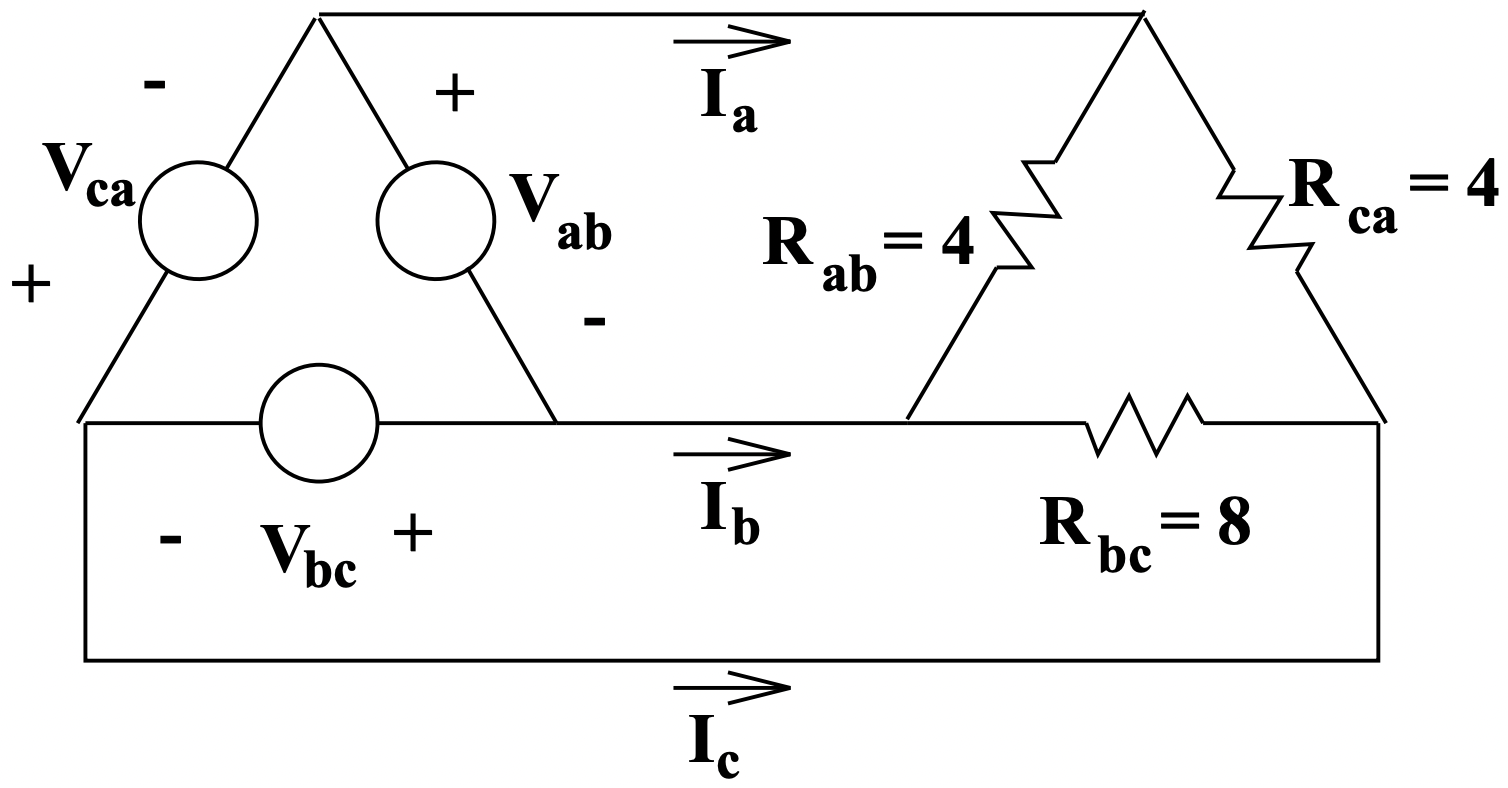    Знімок екрана 2021-07-20 в 1.46.31 PM.pngМалюнок 12: Дельта еквівалент

    Струми в кожному з еквівалентних резисторів бувають:

    \(\ \underline{I}_{1}=\frac{\underline{V}_{a b}}{r_{a b}} \quad \underline{I}_{2}=\frac{\underline{V}_{b c}}{r_{b c}} \quad \underline{I}_{3}=\frac{V_{c a}}{r_{c a}}\)

    Лінійні струми - це лише різниця між струмом в ніжках дельти:

    \ (\\ почати {масив} {l}
    I_ {a} =I_ {1} -I_ {3} =\ sqrt {3} V\ лівий (\ frac {e^ {j\ frac {\ pi} {\ pi} {6}}} {4}} -\ frac {e^ {j\ frac {5\ pi} {6}}} {4}\ право) =\ frac {3} {4} V\\
    I_ {b} =I_ {2} -I_ {1} =\ sqrt {3} V\ лівий (\ frac {-j\ frac {\ pi} {\ pi} {2}}} {8} -\ frac {e^ {j}\ frac {\ pi} {6}} {4}\ праворуч) =-\ ліво (гідророзриву {3} {8} +j\ гідророзриву {1} {4}\ право) V \\
    I_ {c} =I_ {3} -I_ {2} =\ sqrt {3} V\ лівий (\ frac {e^ {5\ frac {5\ pi} {6}}} {4} -\ frac {-j\ frac {\ pi} {2}}} {8}\ праворуч) =\ ліворуч (\ frac {3} {3} 8} -j\ гідророзриву {1} {4}\ право) V
    \ end {масив}\)

    Вони показані на малюнку 13.

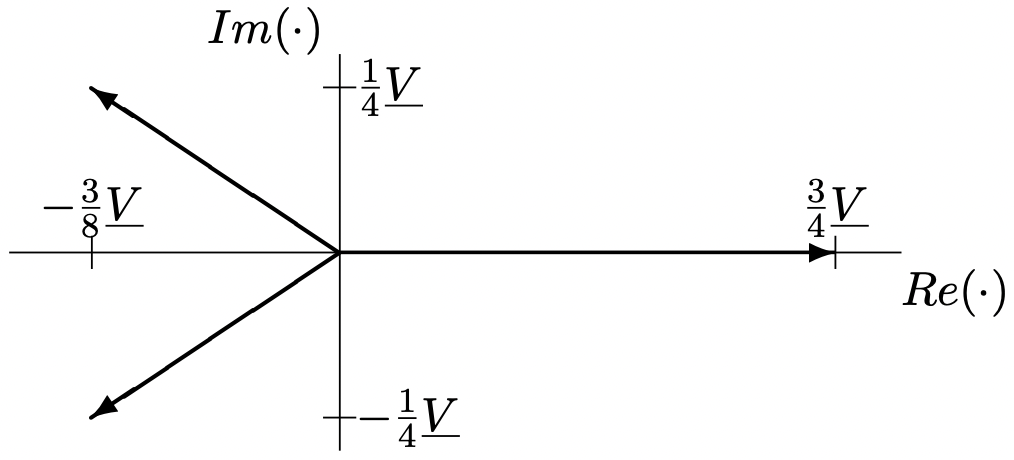    Знімок екрана 2021-07-20 в 1.48.42 PM.pngМалюнок 13: Лінійні струми