6.2: Лінеаризація

Один прямий і потужний метод аналізу нелінійних систем передбачає наближення фактичної системи лінійною. Якщо правильно підібрана апроксимуюча система, вона точно прогнозує поведінку фактичної системи в деякому обмеженому діапазоні рівнів сигналу. Ця методика лінеаризації, заснована на дотичній наближенні до нелінійної залежності, знайома інженерам-електрикам, так як використовується для моделювання багатьох електронних пристроїв. Наприклад, біполярний транзистор є високонелінійним елементом. З метою розробки моделі лінійної області, такої як модель гібрид-пі, для прогнозування поведінки ланцюга цього пристрою, зв'язки між напругою бази до випромінювача та колектором та базовим струмом лінеаризовані. Аналогічно, якщо динамічні показники транзистора представляють інтерес, в модель включаються лінеаризовані ємності, які пов'язують поступові зміни збереженого заряду з поступовими змінами термінальних напруг.

Апроксимуюча функція

Дотична апроксимація базується на використанні рядів Тейлора оцінки цікавить функції. Загалом, передбачається, що вихідна змінна елемента є функцією$N$ вхідних змінних

$$v_O = F(v_{I1}, v_{I2}, ..., v_{IN}) \nonumber$$

Вихідна змінна виражається для невеликих варіацій$v_{i1}, v_{i2}, ..., v_{iN}$ щодо робочих точок вхідної змінної,$V_{I1}, V_{I2}, ..., V_{IN}$ зазначивши, що

$$\begin{array} {rcl} {v_O} & = & {V_O + v_o = F(V_{I1}, V_{I2}, ..., V_{IN})} \\ {} & \ & {+ \sum_{j = 1}^{N} \left.\dfrac{\partial V_O}{\partial V_{Ij}} \right|_{\begin{array} {c} {v_{ij}} \\ {V_{I1}, V_{I2}, ..., V_{IN}} \end{array}}} \\ {} & \ & {+ \dfrac{1}{2!} \sum_{k,l = 1}^{N} \left. \dfrac{\partial^2 V_O}{\partial V_{Ik} \partial V_{Il}} \right |_{\begin{array} {c} {v_{ik}v_{il}} \\ {V_{I1}, V_{I2}, ..., V_{IN}} \end{array}} + \cdots +} \end{array}\label{eq6.2.2}$$

(Нагадаємо, що використані змінні та індексні позначення вказують на те, що$V_o$ є загальною змінною,$V_o$ є її значення операційної точки та$v_o$ її інкрементна складова.)

Розширення$\ref{eq6.2.2}$ рівняння дійсне в будь-якій робочій точці, де існують похідні.

Оскільки різні похідні приймаються обмеженими, функція може бути адекватно апроксимована членами першого порядку в деякому обмеженому діапазоні входів. Таким чином

$$V_O + v_o \simeq F(V_{I1}, V_{I2}, ..., V_{IN}) + \sum_{j = 1}^{N} \left. \dfrac{\partial V_O}{\partial V_{Ij}}\right|_{\begin{array} {c} {v_{ij}} \\ {V_{I1}, V_{I2}, ..., V_{IN}} \end{array}}\label{eq6.2.3}$$

Малюнок 6.1 Лінеаризована блок-схема.

Постійні члени в$\ref{eq6.2.3}$ рівнянні підкладаються, залишаючи

$$v_o \simeq \sum_{j = 1}^{N} \dfrac{\partial V_O}{\partial V_{Ij}}|_{\begin{array} {c} {v_{ij}} \\ {V_{I1}, V_{I2}, ..., V_{IN}} \end{array}}\label{eq6.2.4}$$

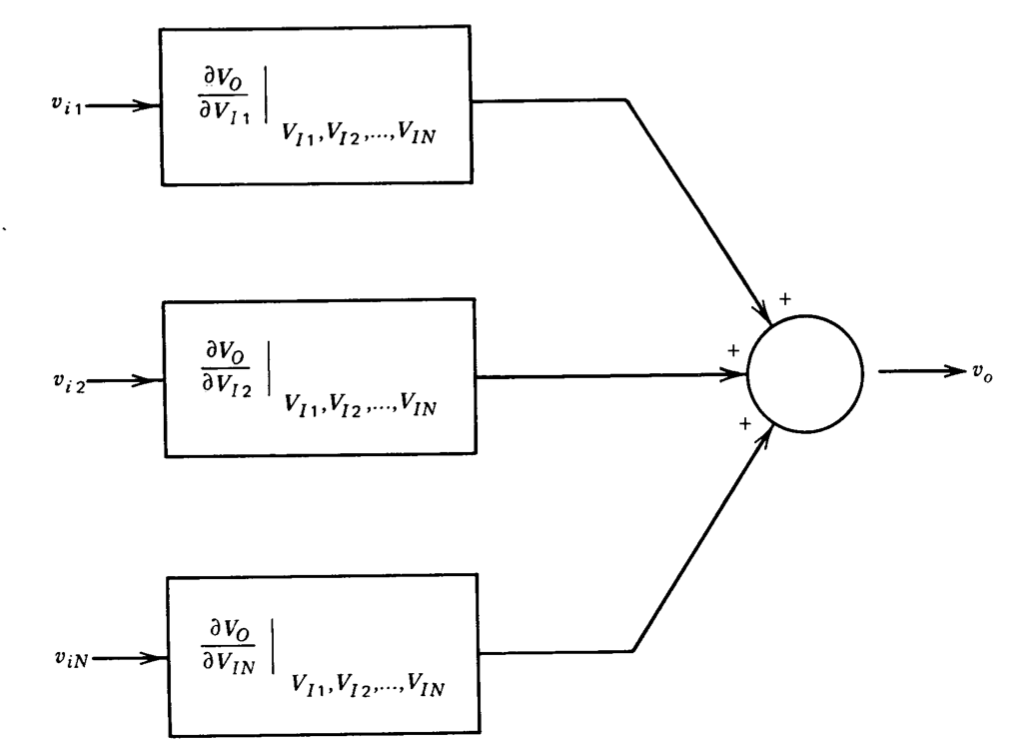
Рівняння$\ref{eq6.2.4}$ може бути використано для розробки лінійно-системних рівнянь, які пов'язують інкрементні, а не загальні змінні, і які наближають інкрементну поведінку фактичної системи в деякому обмеженому діапазоні роботи. Структурна схема взаємозв'язків, що передбачаються рівнянням$\ref{eq6.2.4}$, показана на малюнку 6.1.

Аналіз аналогового дільника

Певні види операцій обробки сигналів вимагають визначення співвідношення двох аналогових змінних, і цю функцію може виконувати дільник. Розподіл часто здійснюється шляхом застосування зворотного зв'язку навколо аналогового множника, і кілька комерційно доступних множників можуть бути перетворені в дільники, зробивши відповідні перемички з'єднання з вихідним підсилювачем, включеним в ці блоки. Можливе з'єднання роздільників даного типу показано на малюнку 6.2$a$.

Малюнок 6.2 Аналоговий дільник. ($a$) Схема. ($b$) Лінеаризована блок-схема.

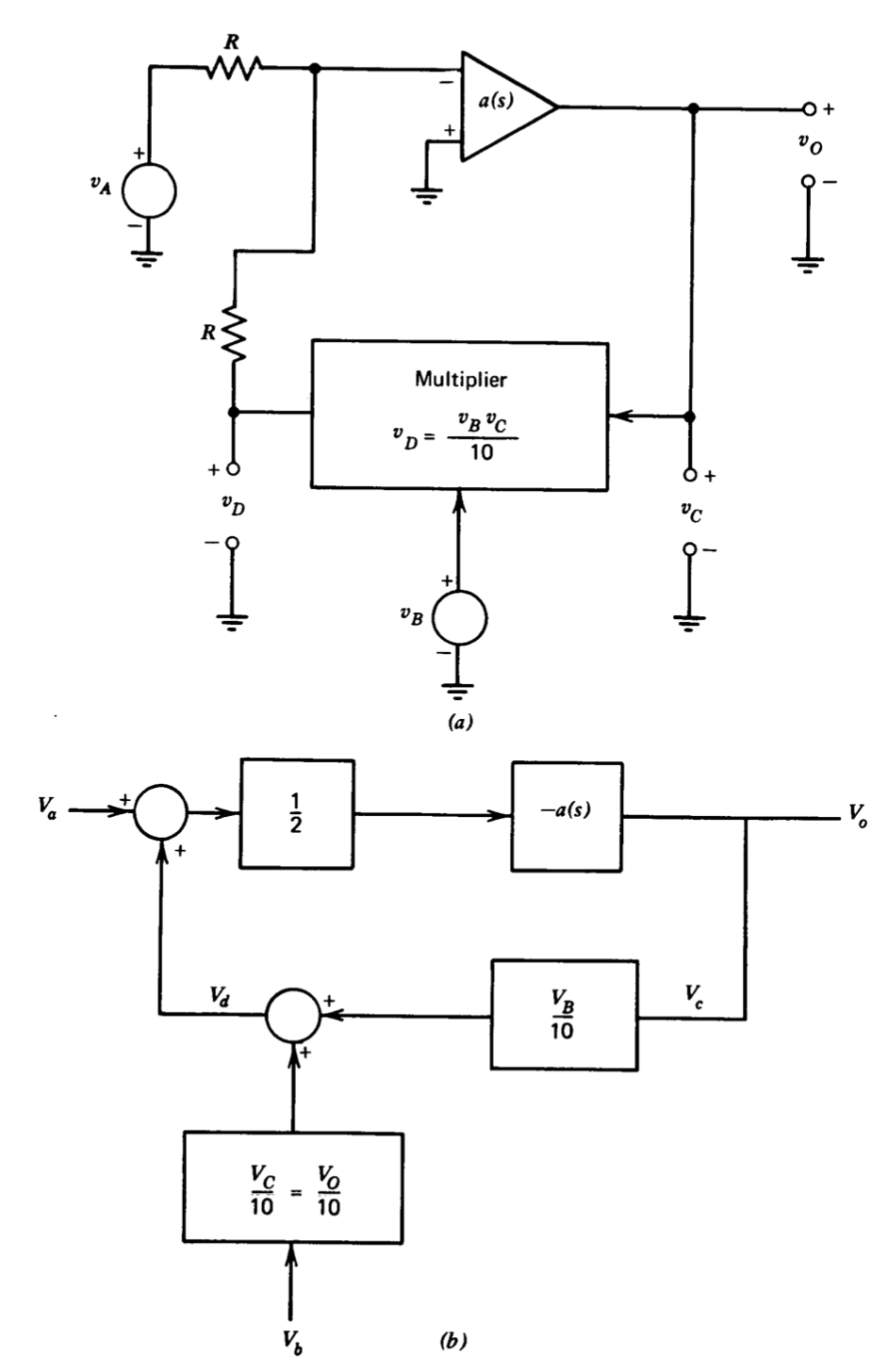
Масштабний коефіцієнт множника, показаний на цьому малюнку, зазвичай використовується, оскільки він забезпечує повномасштабний вихід 10 вольт для двох вхідних сигналів 10 вольт. Передбачається, що сам множиться елемент не має динаміки і таким чином швидкість відгуку системи визначається операційним підсилювачем.

Ідеальну залежність між вхідними та вихідними змінними можна легко визначити за допомогою методу віртуального заземлення. Якщо струм на інвертуючому вході підсилювача невеликий і якщо величина передачі петлі досить висока, щоб напруга на цій клемі була незначною, співвідношення ланцюгів є

$$v_A + v_D = 0\label{eq6.2.5}$$

і

$$v_D = \dfrac{v_B v_C}{10} = \dfrac{v_Bv_O}{10}\label{eq6.2.6}$$

Розв'язування рівнянь$\ref{eq6.2.5}$ і$\ref{eq6.2.6}$ для$v_O$ за термінами$v_A$ і$v_B$ прибутковістю

$$v_O = - \dfrac{10v_A}{v_B} \nonumber$$

Динаміку системи визначають лінеаризацією множинно-елементних характеристик. Застосування рівняння$\ref{eq6.2.3}$ до змінних рівняння$\ref{eq6.2.6}$ показує, що

$$V_D + v_d \simeq \dfrac{V_B V_C}{10} + \dfrac{V_B v_c}{10} + \dfrac{V_C v_b}{10} \nonumber$$

Інкрементна частина цього рівняння

$$v_d = \dfrac{V_B v_c}{10} + \dfrac{V_c v_b}{10} \nonumber$$

Цей зв'язок у поєднанні з іншими обмеженнями ланцюга (припускаючи, що операційний підсилювач має нескінченний вхідний опір і нульовий вихідний опір) використовується для розробки інкрементної блок-схеми, показаної на малюнку 6.2$b$.

Інкрементна$V_o$ залежність від$V_a$, припускаючи, що$v_B$ є постійною, є

$$\dfrac{V_o (s)}{V_a (s)} = \dfrac{-a(s)/2}{1 + V_B a(s)/20}\label{eq6.2.10}$$

Якщо операційна функція передачі підсилювача приблизно однополюсна, так що

$$a(s) = \dfrac{a_0}{\tau s + 1} \nonumber$$

і$a_0$ дуже великий, Рівняння$\ref{eq6.2.10}$ зводиться до

$$\dfrac{V_o (s)}{V_a (s)} \simeq \dfrac{-10/V_B}{(20\tau /V_B a_0)s + 1} \nonumber$$

З цієї функції передачі видно кілька особливостей. По-перше, якщо$V_B$ негативний, то система нестабільна. По-друге, поступова крокова реакція системи першого порядку, з постійною часом$20\tau / V_Ba_0$ секунд. Ці функції вказують на два з багатьох способів того, що нелінійності можуть впливати на продуктивність системи. Стабільність схеми залежить від рівня вхідного сигналу. Крім того, якщо$V_B$ позитивний, перехідний відгук ланцюга стає швидшим зі збільшенням$V_B$, оскільки передача петлі залежить від значення цього входу.

Магнітно-підвісна система

Електромеханічна система, що забезпечує другий приклад лінеаризованого аналізу, проілюстрована на малюнку 6.3. Призначення системи - підвісити залізну кульку в полі електромагніту. Враховується тільки вертикальний рух кулі.

Малюнок 6.3 Магнітно-підвісна система.

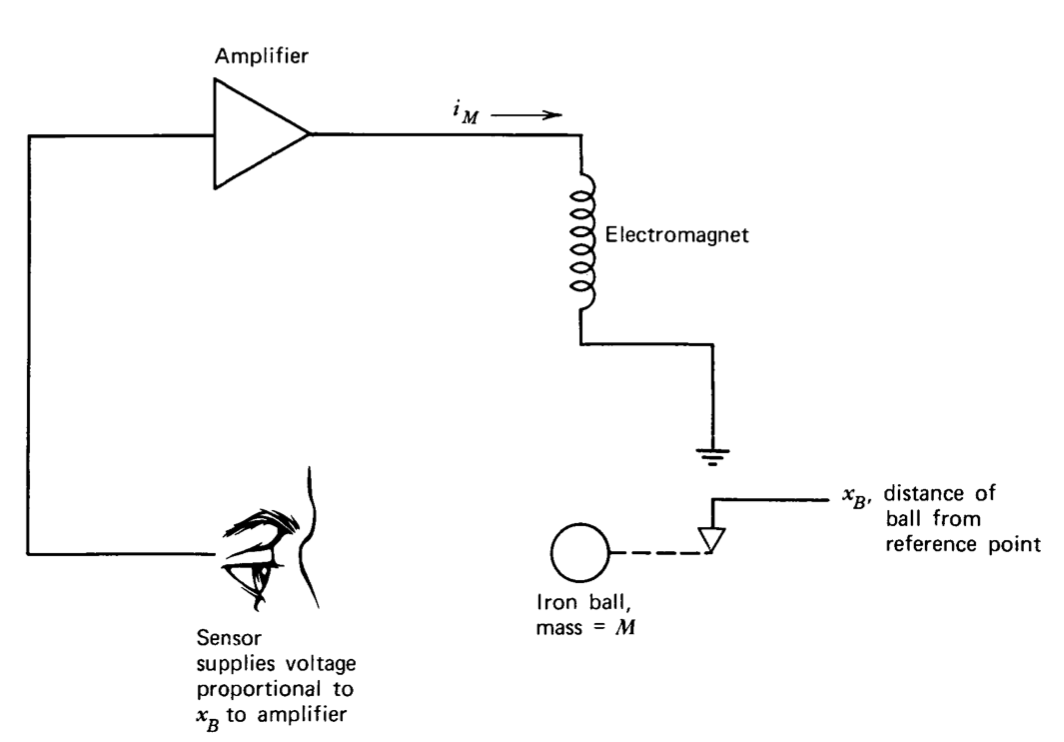
Для того, щоб призупинити кулю необхідно скасувати спадну гравітаційну силу на кулю з висхідною силою, що виробляється магнітом. Зрозуміло, що стабілізація постійним струмом неможлива, так як поки величина,$x_B$ для якої відсутня чиста сила на кульку, існує, невелике відхилення від цього положення змінює магнітну силу таким чином, щоб прискорити кульку далі від рівноваги. Цей ефект можна скасувати, відповідним чином контролюючи струм магніту як функцію вимірюваного положення кульки.

Для певних геометрій та при відповідному виборі опорного положення для магнітна сила$x_B$, що$f_M$ чиниться на кулю у напрямку вгору, становить

$$f_M = \dfrac{Ci_M^2}{x_B^2} \nonumber$$

де$C$ константа.
Припускаючи$x_b$ поступові зміни і$i_m$ про значення робочої точки$X_B$ і$I_M$, відповідно,

$$f_M = F_M + f_m = \dfrac{CI_M^2}{X_B^2} + \dfrac{2CI_M}{X_B^2} i_m - \dfrac{2CI_M^2}{X_B^3} x_b + \text{ higher-order terms}\label{eq6.2.14}$$

Рівняння руху м'яча

$$\dfrac{Md^2 x_B}{dt^2} = Mg - f_M\label{eq6.2.15}$$

де$g$ - прискорення сили тяжіння. Рівновага або значення операційної точки вибираються так, щоб

$$Mg = \dfrac{CI_M^2}{X_B^2} \nonumber$$

Коли ми поєднуємо рівняння$\ref{eq6.2.14}$$\ref{eq6.2.15}$ і припускаємо операцію про точку рівноваги, лінеаризоване співвідношення між інкрементними змінними стає

$$\dfrac{Md^2 x_b}{dt^2} - \dfrac{2CI_M^2}{X_B^3} x_b = -\dfrac{2CI_M}{X_B^2}i_m\label{eq6.2.17}$$

$\ref{eq6.2.17}$Рівняння перетворюється і переставляється як

$$\dfrac{s^2 X_b(s)}{k^2} - X_b (s) = X_b(s) \left (\dfrac{s}{k} + 1 \right ) \left (\dfrac{s}{k} - 1 \right ) = -\dfrac{X_B}{I_M} I_m (s)\label{eq6.2.18}$$

де$k^2 = 2CI_M^2 / MX_B^3$.

Рисунок 6.4 Лінеаризована блок-схема для системи Рисунок 6.3.

Зворотній зв'язок застосовується до системи, роблячи$i_m$ лінійну функцію$x_b$, або

$$I_m (s) = a(s) X_b (s)\label{eq6.2.19}$$

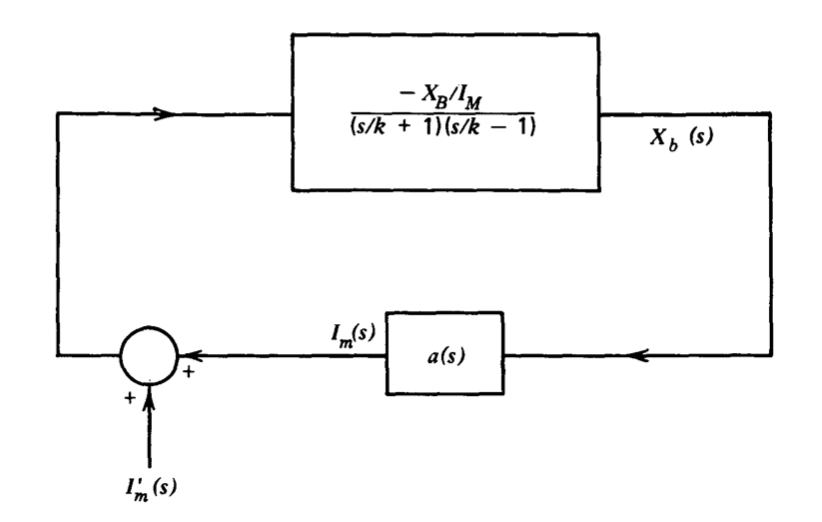
Рівняння$\ref{eq6.2.18}$ і$\ref{eq6.2.19}$ використовуються для малювання лінеаризованої блок-схеми, показаної на малюнку 6.4. [$I_m'(s)$Вхідні дані використовуються як тестовий вхід пізніше в аналізі.]

Контурна передача для цієї системи

$$L(s) = -\dfrac{a(s) \dfrac{X_B}{I_M}}{\left (\dfrac{s}{k} + 1 \right ) \left (\dfrac{s}{k} - 1 \right )} \nonumber$$

містить полюс в правій половині площині, який відображає той факт, що система нестабільна при відсутності зворотного зв'язку. Наївна спроба стабілізації для цього типу систем передбачає скасування правого полуплоского полюса з нулем$a(s)$. Хоча таке скасування працює, коли особливості, про які йде мова, знаходяться в лівій половині площині, вона приречена на провал в цьому випадку. Хоча полюс, здавалося б, може бути видалений з передачі петлі за допомогою цього методу, (Допуски компонентів виключають точне скасування в будь-якій, крім математичної системи.) Розглянемо функцію передачі замкнутого циклу, яка відноситься$X_b$ до порушення$I_m'$.

Якщо$a(s)$ вибрано як$a'(s) (s/k - 1)$, ця функція перенесення

$$\dfrac{X_b (s)}{I_m' (s)} = \dfrac{\dfrac{-X_B/I_M}{(s/k + 1)(s/k - 1)}}{1 + \dfrac{a'(s) X_B/I_M}{s/k + 1}}\label{eq6.2.21}$$

Рівняння$\ref{eq6.2.21}$ містить правий напівплощинний полюс, що має на увазі експоненціально зростаючі відповіді для Xb, хоча це зростання не спостерігається як зміна$i_m$.

Малюнок 6.5 Діаграми кореневих локусів для магнітно-підвісної системи. ($a$1) Uncom покарається. ($b$) З компенсацією свинцю.

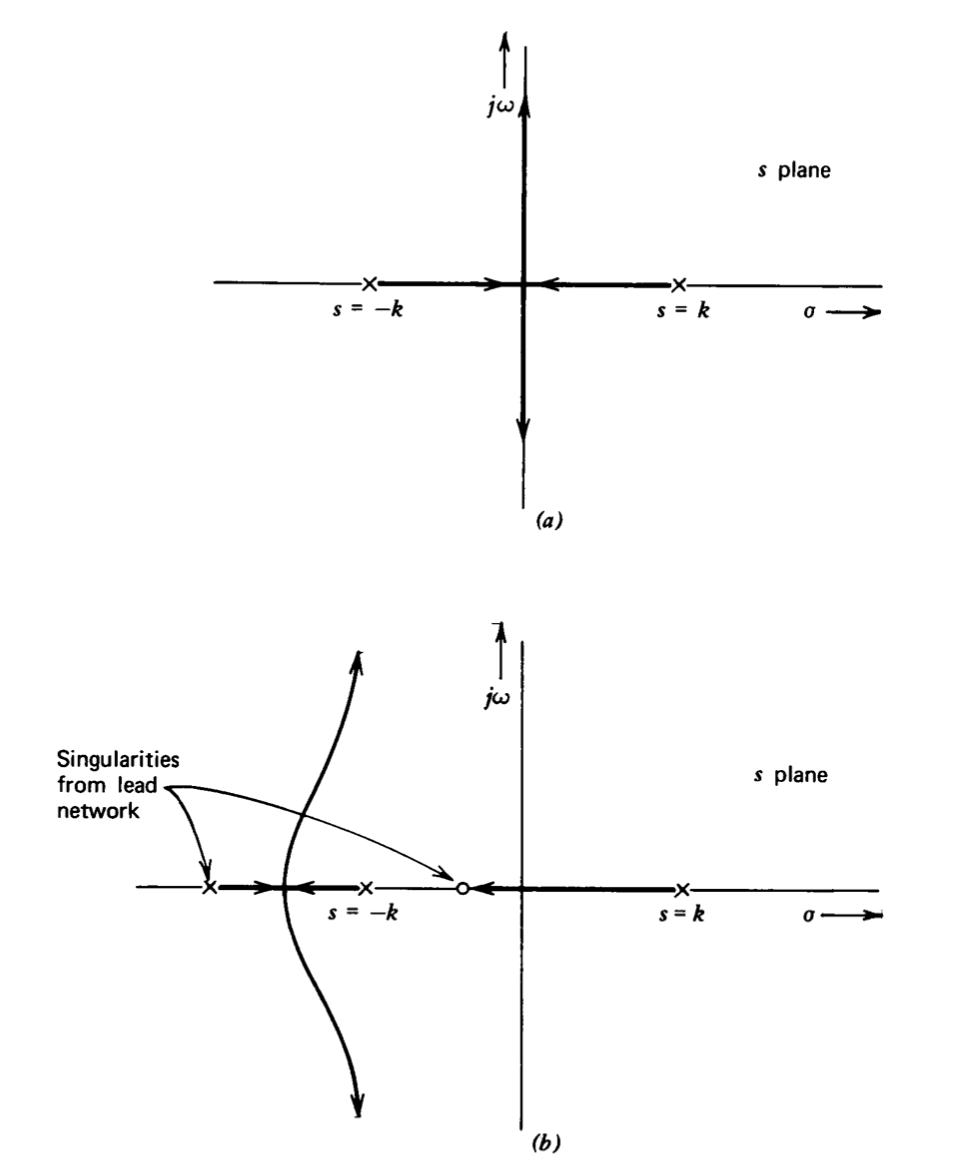
Задовільний метод компенсації системи можна визначити, розглянувши діаграми корінь-локус, показані на малюнку 6.5. Малюнок 6.5$a$ являє собою діаграму для частотно-незалежного зворотного зв'язку с$a(s) = a_0$. У міру$a_0$ збільшення два полюса збираються разом і розгалужуються уздовж уявної осі. Ця діаграма показує, що можна зняти полюс замкнутого контуру з правої половини площини, якщо ao правильно обраний. Однак полюси не можуть бути переміщені в ліву половину площини, і, таким чином, система проявляє неослаблені коливальні реакції. Система може бути стабілізована, включивши функцію передачі свинцю в$a(s)$. Можна переміщати всі полюси замкнутого контуру в ліву половину площини при будь-яких параметрах свинцевої мережі в поєднанні з досить високим значенням$a_0$. Рисунок 6.5$b$ ілюструє кореневі траєкторії для одного можливого вибору особливостей свинцевої мережі.