5.3: Компенсація відгуків

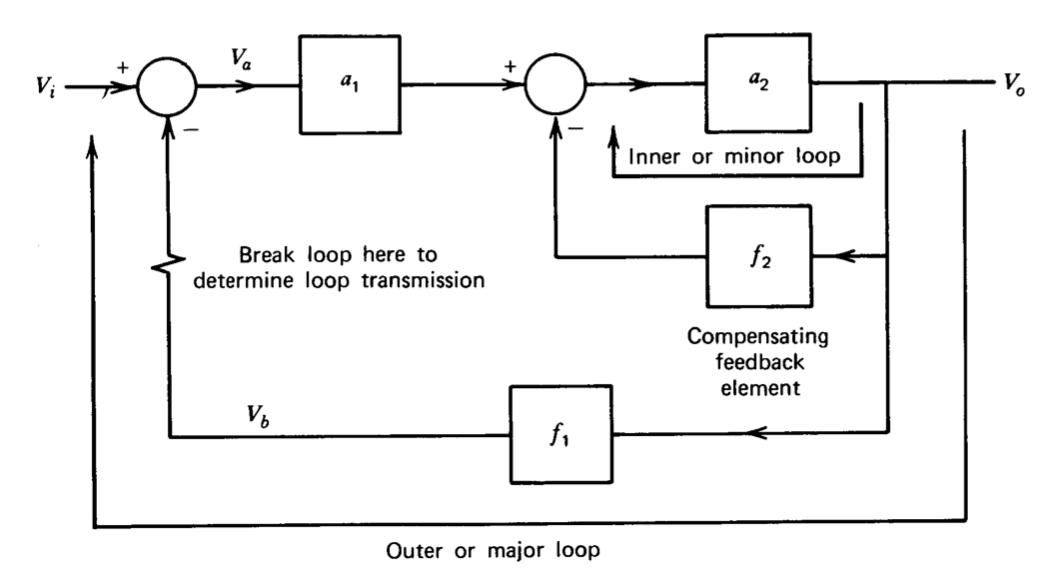
Серійна компенсація досягається шляхом додавання каскадного елемента до одноконтурної системи зворотного зв'язку. Компенсація зворотного зв'язку реалізується шляхом додавання елемента зворотного зв'язку, який створює двоконтурну систему. Одна з можливих топологій проілюстрована на малюнку 5.20. Функція передачі замкнутого циклу для цієї системи

$$\dfrac{V_o}{V_i} = \dfrac{a_1 a_2/(1 + a_2 f_2)}{1 + a_1 a_2f_1/(1 + a_2 f_2)} \nonumber$$

Малюнок 5.20 Топологія для компенсації зворотного зв'язку.

Послідовно компенсована система з елементом зворотного зв'язку, ідентичним елементу зворотного зв'язку з основним контуром малюнка 5.20, показана на малюнку 5.21. Два елементи зворотного зв'язку ідентичні, оскільки передбачається, що від двох систем потрібна однакова ідеальна функція передачі замкнутого циклу.

Малюнок 5.21 Серійно-компенсована система.

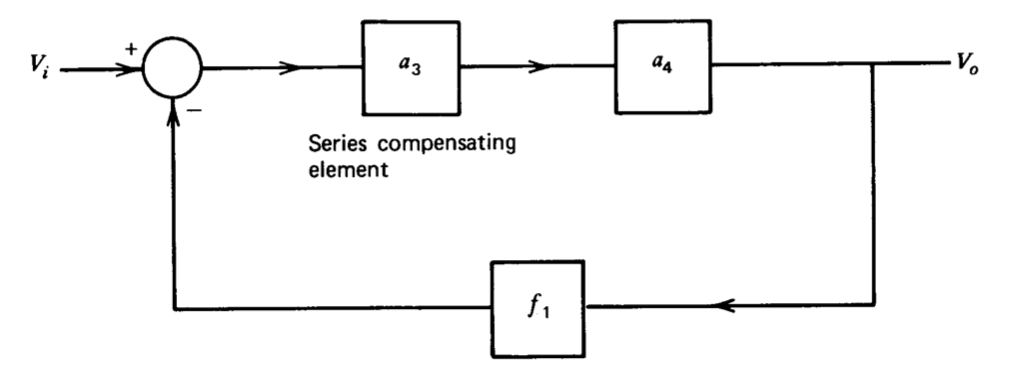
Функція передачі замкнутого циклу для послідовно компенсованої системи є

$$\dfrac{V_o}{V_i} = \dfrac{a_3 a_4}{1 + a_3 a_4 f_1} \nonumber$$

Функції передачі замкнутого циклу зворотного зв'язку і послідовно компенсованих систем будуть рівними, якщо вибрати$f_2$ так, щоб

$$a_3 = \dfrac{a_1 a_2}{(1 + a_2 f_2) a_4}\label{eq5.3.3}$$

або

$$f_2 = \dfrac{a_1 a_2 - a_3 a_4}{a_2 a_3 a_4}\label{eq5.3.4}$$

Вищевказаний аналіз свідчить про те, що одним із способів вибору відповідної компенсації зворотного зв'язку є спочатку визначення компенсації серії, яка дає прийнятну продуктивність, а потім перетворити на еквівалентну компенсацію зворотного зв'язку. На практиці такий підхід зазвичай не використовується, а, скоріше, послідовна компенсація визначається для використання потенційних переваг цього методу.

Ми побачимо, що якщо операційний підсилювач призначений для прийняття компенсації зворотного зв'язку, використання цієї техніки часто призводить до продуктивності, що перевершує ту, яка може бути досягнута за допомогою компенсації серії. Часта перевага компенсації зворотного зв'язку не є наслідком будь-якої помилки в математиці, яка призвела до еквівалентності Рівняння$\ref{eq5.3.3}$,$\ref{eq5.3.4}$ а натомість є результатом практичних факторів, які не входять в ці розрахунки. Наприклад, компенсуючу мережу, необхідну для отримання заданої продуктивності із замкнутим контуром, часто легше визначити та реалізувати і може бути менш чутливою до змін інших параметрів підсилювача у випадку підсилювача з компенсацією зворотного зв'язку. Подібним чином проблеми, пов'язані з нелінійністю та шумом, часто посилюються послідовною компенсацією, але насправді можуть бути зменшені компенсацією зворотного зв'язку.

Підхід до пошуку типу компенсації зворотного зв'язку, який слід використовувати в даному додатку, полягає у розгляді негативу петлевого транс-місії для системи рис. 5.20. Ця кількість

$$\dfrac{V_b}{V_a} = a_1 f_1 \dfrac{a_2}{1 + a_2 f_2} \nonumber$$

Якщо внутрішній цикл стабільний (тобто якщо не$1 + a_2f_2$ має нулів у правій половині$s$ площини), то

$$\dfrac{V_b (j \omega)}{V_a (j \omega)} \simeq \dfrac{a_1 (j \omega) f_1 (j \omega)}{f_2 (j \omega)} \ \ \ \ |a_2 (j \omega) f_2 (j \omega)| \gg 1\label{eq5.3.6}$$

і

$$\dfrac{V_b (j \omega)}{V_a (j \omega)} \simeq a_1 (j \omega) f_1 (j \omega)a_2 (j \omega) \ \ \ \ |a_2 (j \omega) f_2 (j \omega)| \ll 1\label{eq5.3.7}$$

На практиці параметри системи часто підбираються так, щоб величина передачі другорядної петлі була великою на частотах, де величина передачі основного контуру близька до одиниці. Потім наближення рівняння$\ref{eq5.3.7}$ може бути використано для визначення значення$f_2$, яке забезпечує стабільність системи.

Малюнок 5.22 Операційний підсилювач. ($a$) Модель. ($b$) Блок-схема.

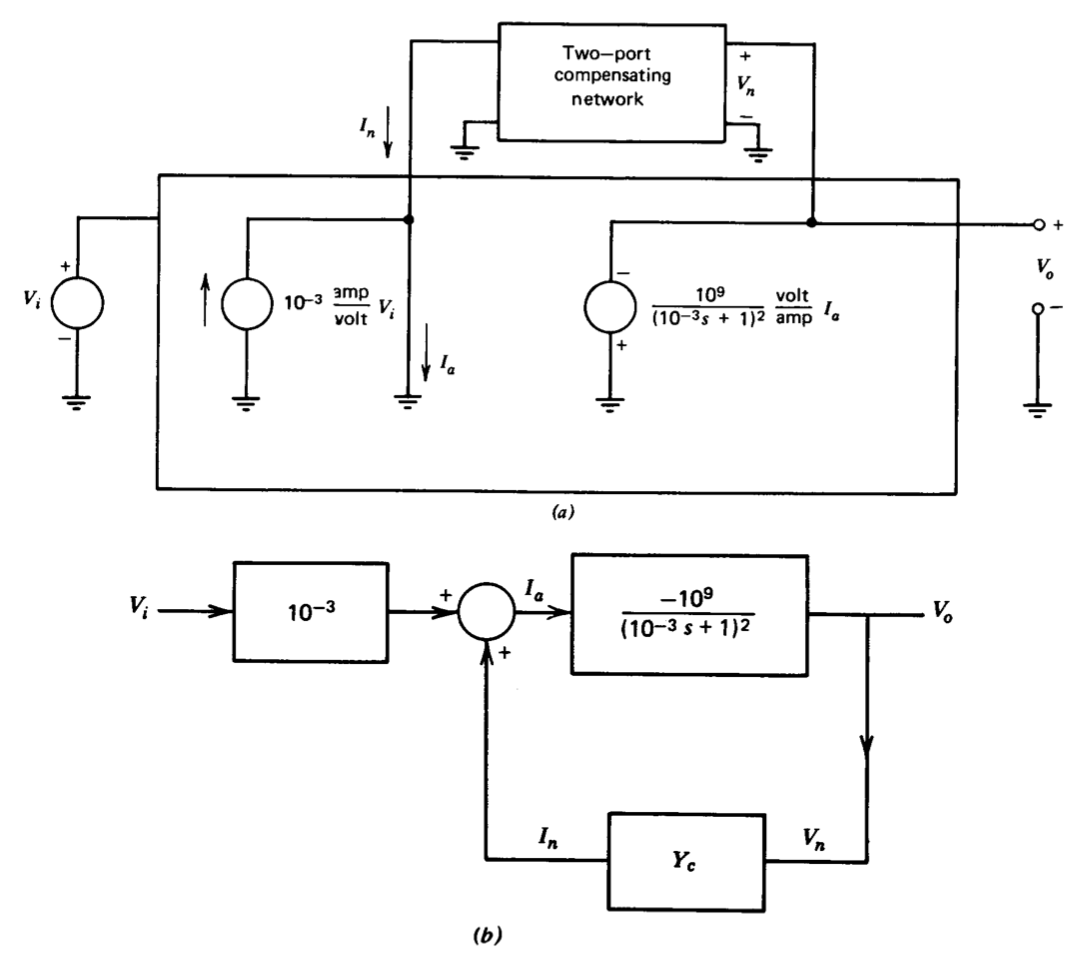
Простий приклад компенсації зворотного зв'язку дає модель операційно-підсилювача, показана на малюнку 5.22$a$. Модель являє собою ідеалізацію загальної топології підсилювача, яка буде детально досліджена в наступних розділах. Модельований підсилювач включає перший етап з широкою пропускною здатністю порівняно з рештою ланцюга, що рухається на другий етап, який має

відносно низький вхідний опір, який домінує в некомпенсованій динаміці підсилювача. Компенсація забезпечується двопортовою мережею, яка підключена навколо другого ступеня і яка утворює незначний шлейф. Ця мережа обмежена бути пасивною. Блок-схема підсилювача показана на малюнку 5.22$b$. $Y_c$Величина - допуск передачі короткого замикання компенсуючої мережі,$I_n/ V_n$. (Угода, що використовується для визначення,$Y_c$ знаходиться в дисперсії з нормальним двопортовим позначенням, що змінить напрямок посилання для$I_n$. Ця форма використовується, оскільки вона призводить до меншої кількості знаків мінуса в наступних рівняннях.)

Якщо компенсація не використовується, функція передачі разомкнутого контуру для підсилювача є

$$\dfrac{V_o (s)}{V_i (s)} = -\dfrac{10^6}{(10^{-3} s + 1)^2} \nonumber$$

Якщо провід підключений від виходу підсилювача назад до його входу, створюючи великий шлейф з$f = 1$, запас фази результуючої системи приблизно$0.12^{\circ}$.

Коли компенсація зворотного зв'язку включена, блок-схема показує, що функція передачі підсилювача є

$$\dfrac{V_o (s)}{V_i (s)} = \dfrac{-10^6/(10^{-3} s + 1)^2}{1 + 10^9 Y_c/(10^{-3} s + 1)^2}\label{eq5.3.9}$$

Один із способів покращити запас фази цього підсилювача при використанні в з'єднанні зворотного зв'язку полягає в тому, щоб$V_o (s)/V_i(s)$ домінувати один полюс. Рівняння$\ref{eq5.3.9}$ показує, що

$$\dfrac{V_o (j\omega)}{V_i (j\omega)} \simeq \dfrac{-10^{-3}}{Y_c (j\omega)} \text{ when } \left | \dfrac{10^9 Y_c (j\omega)}{(10^{-3} j \omega + 1)^2} \right | \gg 1 \nonumber$$

Якщо для компенсуючої мережі$C$ використовується один конденсатор,$Y_c = Cs$ і

$$\dfrac{Y_o (j\omega)}{Y_i (j\omega)} \simeq \dfrac{-10^{-3}}{j \omega C} \nonumber$$

для всіх частот таких, що

$$\left |\dfrac{10^9 Cj \omega}{(10^{-3} j \omega + 1)^2} \right | \gg 1\nonumber$$

Точний вираз для функції передачі розімкнутого контуру підсилювача з цією компенсацією є

$$\dfrac{V_o (s)}{V_i (s)} = \dfrac{-10^6 / (10^{-3} s + 1)^2}{1 + 10^9 Cs/ (10^{-3} s + 1)^2} = \dfrac{-10^6}{10^{-6} s^2 + (2 \times 10^{-3} + 10^9 C)s + 1} \nonumber$$

Якщо для конденсатора використовується 840-пФ$C$, передавальна функція стає

$$\dfrac{V_o (s)}{V_i (s)} = \dfrac{-10^6}{(0.84s + 1)(1.19 \times 10^{-6} s + 1)} \nonumber$$

і фазовий запас принаймні$45^{\circ}$ забезпечується для частотно-незалежного зворотного зв'язку з будь-якою величиною менше, ніж одна застосовується навколо підсилювача. При цьому значенні компенсуючого елемента зворотного зв'язку,

$$-\dfrac{V_o(j \omega)}{V_i (j \omega)} \simeq \dfrac{1.19 \times 10^6}{j\omega} = \dfrac{10^{-3}}{Cj\omega} = \dfrac{10^{-3}}{Y_c (j\omega)} \nonumber$$

на будь-якій частоті між 1,19 радіанів в секунду і$0.84 \times 10^6$ радіанами в секунду. Дві обмежувальні частоти - це ті, при яких величина компенсаційного контуру передачі одна. Важливим моментом є те, що зворотний зв'язок незначного контуру контролює передавальну функцію підсилювача протягом майже шести десятиліть частоти. Відзначимо також, що навіть незважаючи на те, що домінантний полюс був створений за допомогою компенсації зворотного зв'язку, одинична частота посилення компенсованого підсилювача (приблизно$8 \times 10^5$ радіани в секунду) залишається близькою до некомпенсованого значення$10^6$ радіанів в секунду.

Компенсація зворотного зв'язку - це потужна і часто використовувана компенсаційна техніка для сучасних операційних підсилювачів. Кілька прикладів такого типу компенсації будуть надані після того, як будуть описані топології схеми репрезентативних підсилювачів.

ПРОБЛЕМИ

Вправа$\PageIndex{1}$

Операційний підсилювач має функцію передачі з відкритим контуром

$$a(s) = \dfrac{2 \times 10^5}{(0.1s + 1)(10^{-5} s + 1)^2}\nonumber$$

Спроектуйте з'єднання, яке використовує цей підсилювач для забезпечення ідеального посилення - 10. Включіть положення про зниження величини передачі петлі так, щоб перевищення у відповідь на одиничний крок становило 10%. Ви можете використовувати криві малюнка 4.26 як допоміжний засіб для визначення необхідного загасання.

Вправа$\PageIndex{2}$

Малюнок 5.23 Оцінка шуму на виході інвертуючого підсилювача. ($a$) Підключення інвертора. ($b$) Метод моделювання шуму на вході підсилювача.

Підключається операційний підсилювач так, як показано на малюнку 5.23$a$. Значення$\alpha$ регулюється для контролю стабільності з'єднання. Припустимо, що шум, пов'язаний з підсилювачем, можна змоделювати так, як показано на малюнку 5.23$b$. Оцініть шум на виході підсилювача як функцію$\alpha$, нехтуючи навантаженням на вході і виході підсилювача. Відзначимо, що збільшення шуму на виході підсилювача передбачає зменшення відношення сигнал/шум, так як коефіцієнт посилення від входу до виходу по суті не залежить від$\alpha$.

Вправа$\PageIndex{3}$

Малюнок 5.24 Система зворотного зв'язку з домінуючим полюсом.

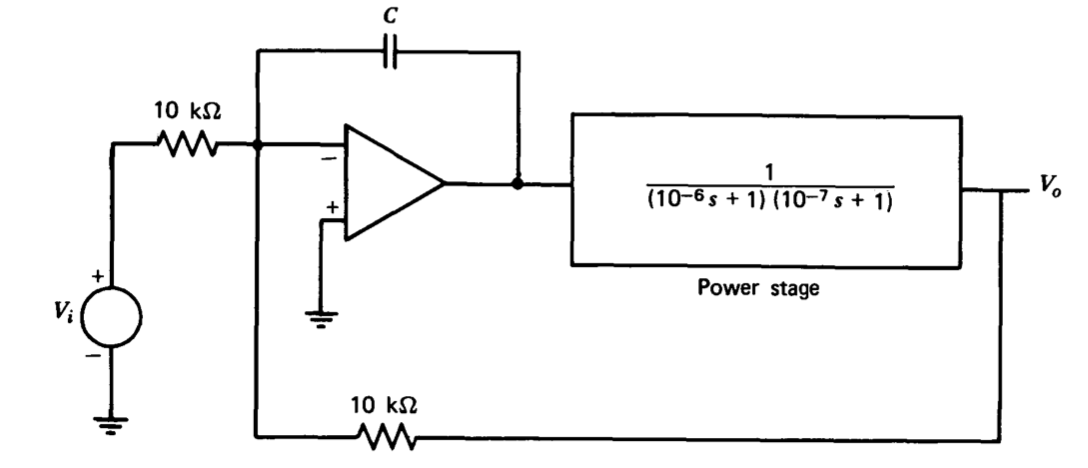
Певний підсилювач зворотного зв'язку можна змоделювати, як показано на малюнку 5.24. Можна припустити, що операційний підсилювач, включений в цю схему, ідеальний. Виберіть значення для конденсатора$C$, що призводить до запасу фази системи$45^{\circ}$.

Вправа$\PageIndex{4}$

Малюнок 5.25 Система регулювання швидкості. ($a$) Системна діаграма. ($b$) Модель двигуна.

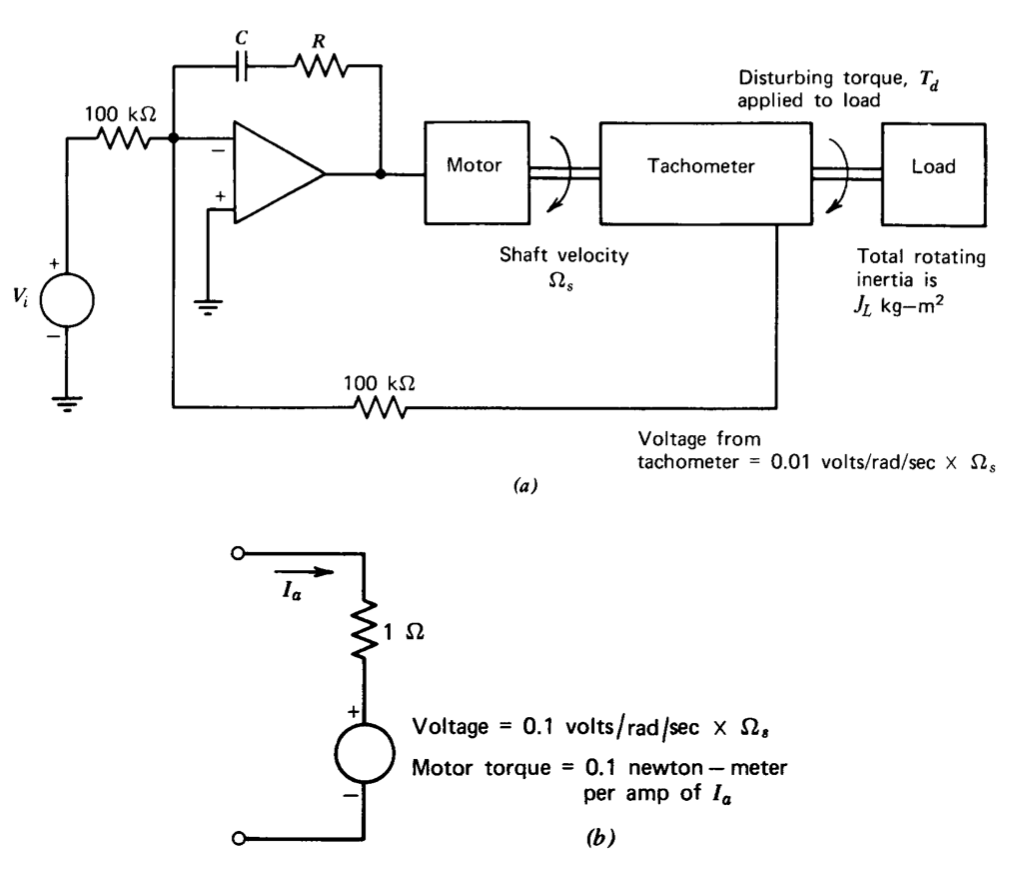
Система регулювання швидкості поєднує в собі операційний підсилювач великої потужності в контурі з двигуном і тахометром, як показано на малюнку 5.25. Тахометр забезпечує напругу, пропорційну швидкості вихідного вала, і ця напруга використовується як сигнал зворотного зв'язку для впливу на регулювання швидкості.

1. Намалюйте блок-схему для цієї системи, яка включає ефекти тривожного крутного моменту.
2. Визначте компенсуючі значення компонентів ($R$і$C$) як функцію$J_L$ так, щоб передача контуру системи була$- 100/s$.
3. Показати, що при цьому типі петльової передачі стабільна вихідна швидкість не залежить від будь-якого постійного моменту навантаження.
4. Використовуйте аналіз коефіцієнтів помилок, щоб показати, що система менш чутлива до змінних у часі тривожних моментів, коли$J_L$ використовуються більші значення. Припустимо, що$R$ і$C$ змінюються з$J_L$ для підтримки петлі передачі, зазначеної в частині$b$.

Вправа$\PageIndex{5}$

Малюнок 5.26 Мережа Lag-Lead.

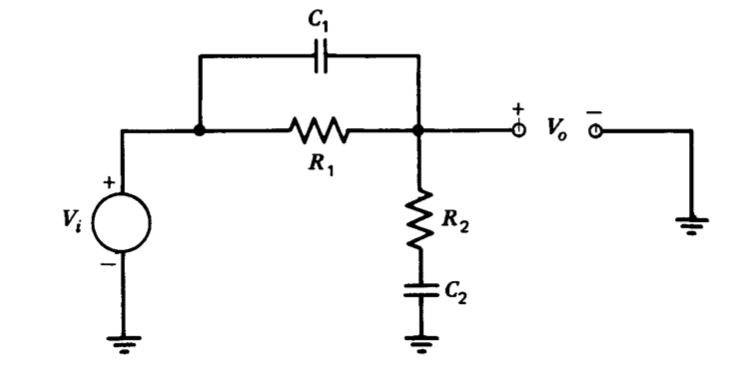
Показати, що мережа, проілюстрована на малюнку 5.26, може бути використана для об'єднання функції перенесення затримки з функцією передачі відведення, розташованої на більш високій частоті. Визначте параметри мережі, які призведуть до функції передачі

$$\dfrac{V_o (s)}{V_i (s)} = \dfrac{(0.1s + 1)(10^{-2} s + 1)}{(s + 1)(10^{-3} s + 1)}\nonumber$$

Вправа$\PageIndex{6}$

Циклічна передача системи зворотного зв'язку може бути наближена як

$$L(s) = -\dfrac{10^6}{s^2} \nonumber$$

в безпосередній близькості від одиниці-посилення частоти. Припустимо, що до транс-місії циклу може бути додана функція передачі відведення (Рівняння 5.2.4) зі значенням a = 10. Як повинна бути розташована передавальна функція, щоб максимізувати запас фази? Які значення фазового запасу і частоти кросовера результат?

Вправа$\PageIndex{7}$

Використовуйте блок-схему, щоб показати, що функція передачі затримки може бути введена в петлю передачі підсилювача посилення з десяти (рис. 5.9) шляхом шунтування$R$ -значного резистора відповідною мережею.

1. Виберіть параметри мережі так, щоб передача петлі системи задавалася рівнянням 5.2.17.
2. Знайдіть функцію передачі із замкнутим контуром та побудуйте крокову реакцію із замкнутим контуром для підсилювача посилення десяти, використовуючи значення, знайдені частково$a$, припускаючи, що характеристики операційного підсилювача ідеальні.
3. Оцініть крокову реакцію із замкнутим контуром для цього з'єднання, припускаючи, що функція передачі розімкнутого контуру підсилювача відповідає рівнянню 5.2.12.
4. Порівняйте продуктивність лаг-компенсованої системи, розробленої в цій задачі, з показаною на малюнку 5.13, враховуючи як стабільність, так і ідеальну функцію передачі із замкнутим контуром двох з'єднань.

Вправа$\PageIndex{8}$

У розділі 5.2.4 було зазначено, що альтернативні можливості компенсації підсилювача посилення десяти включають зниження величини передачі петлі на всіх частотах в рази 6,2 і зниження розташування нижчечастотного полюса в передавальній функції петлі в 6,2 рази вибір відповідних параметрів лаг-мережі.

1. Визначте топології та значення компонентів для реалізації обох цих схем компенсації.
2. Намалюйте петлі-передачі Боде ділянки для цих двох способів компенсації.
3. Порівняйте відносну стійкість, отриману цими методами, з тією, що забезпечується компенсацією затримки, описаною в розділі 5.2.4.

Вправа$\PageIndex{9}$

Негативний контур передачі для компенсованого свинцевим коефіцієнтом посилення десяти підсилювача, описаного в розділі 5.2.4, є

$$a(s)f(s) = \dfrac{5 \times 10^4 (10\tau s + 1)}{(s + 1)(10^{-4} s + 1)(10^{-5} s + 1)(\tau s + 1)}\nonumber$$

де$\tau$ визначається значення резистора і конденсатора, використовуваних в мережі зворотного зв'язку (див. Рівняння 5.2.15). Використовуйте кореневі контури для оцінки стабільності підсилювача посилення десяти в залежності від параметра$\tau$. Знайдіть значення$\tau$, яке максимізує коефіцієнт демпфування домінуючої пари полюсів. Примітка. Оскільки для завершення цієї задачі необхідно множник поліномів третього та четвертого порядку, запропоновано використання машинних обчислень. Також запропоновано чисельні розрахунки для оцінки максимального коефіцієнта демпфування.

Вправа$\PageIndex{10}$

Негативний контур передачі для лаг-компенсованого підсилювача дорівнює

$$a(s)f(s) = \dfrac{5 \times 10^4 (\tau s + 1)}{(s + 1)(10^{-4} s + 1)(10^{-5} s + 1)(\alpha \tau s + 1)}\nonumber$$

У розділі 5.2.4 було показано, що розумна$\alpha = 6.2$ стабільність призводить до$\tau$ того, що значення цього знаходить нуль лаг-функції на коефіцієнт 10 нижче перехресного. Використовуйте кореневі контури для оцінки стійкості як функції нульового розташування$(1/\tau)$ для$\alpha = 6.2$. Примітка щодо доцільності машинних обчислень, згаданих у задачі Р5.9, також застосовується до цього розрахунку.

Вправа$\PageIndex{11}$

Визначте перші три коефіцієнти похибки для чотирьох петлевих передач підсилювача посилення з десяти, описаних рівнянням 5.2.18 через 5.21. Припустимо, що компенсація відведення отримана на шляху зворотного зв'язку (див. Розділ 5.2.4), тоді як всі інші компенсації можна вважати розташованими на прямому шляху.

Вправа$\PageIndex{12}$

Система зворотного зв'язку включає в себе фактор

$$\dfrac{(s^2/12) - (s/2) + 1}{(s^2/12) + (s/2) + 1}\nonumber$$

в його петлі передачі.

Припустимо, що у вас є повна свобода у виборі величини петлі d-c і вибору додаткових особливостей в петлі передачі. Визначте тип компенсації, яка дозволить максимально підвищити дечутливість даної системи.

Вправа$\PageIndex{13}$

Обчисліть час осідання (до 1% від кінцевого значення для крокового входу) для підсилювача посилення десяти з компенсацією затримки (Рівняння 5.2.17). Протипоставте це значення з показником системи першого порядку з однаковою частотою кросовера.

Вправа$\PageIndex{14}$

Малюнок 5.27 Модель операційно-підсилювача.

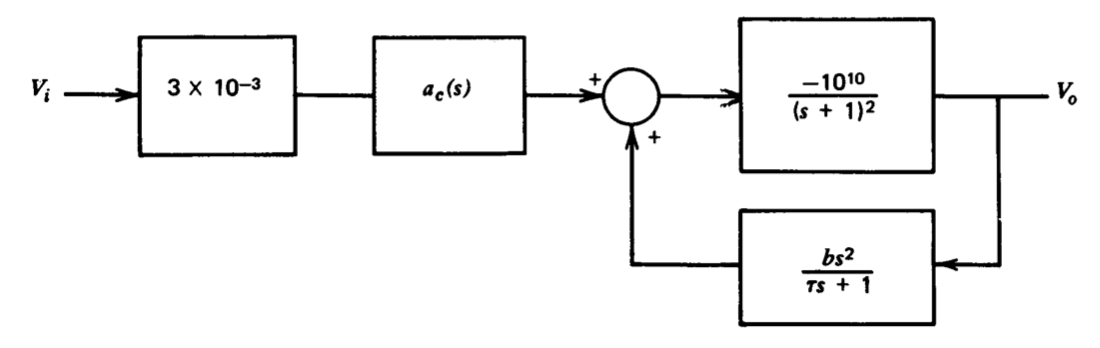
Модель операційного підсилювача з використанням компенсації незначного контуру показана у вигляді блок-схеми на малюнку 5.27.

(а) Припустимо, що послідовний компенсуючий елемент має передавальну функцію$a_c(s) = 1$. Знайти значення для$b$ і$\tau$ такі, що основний цикл, утворений подачею$V_o$ безпосередньо назад,$V_i$ матиме перехресну частоту$10^3$ радіанів в секунду, приблизно$55^{\circ}$ від фазового запасу, і максимальну дечутливість на частотах нижче кросовера за умови цих обмеження. Намалюйте графік Боде з розімкнутим контуром для підсилювача з цими значеннями для$b$ і$\tau$.

(б) Тепер припустимо, що$b = 0$. Чи можете ви знайти значення$a_c(s)$ для. що призводить до тих самих асимптотичних характеристик величини розімкнутого циклу, що і ви отримали частково$a$, з урахуванням обмеження, що$|a_c (j \omega)| \le 1$ для всіх$\omega$?

Вправа$\PageIndex{15}$

Малюнок 5.28 Підсилювач з керованою динамікою. PIN-номери призначені для пакетів TO-99 та minidip.

Малюнок 5.29 Інвертування конфігурації.

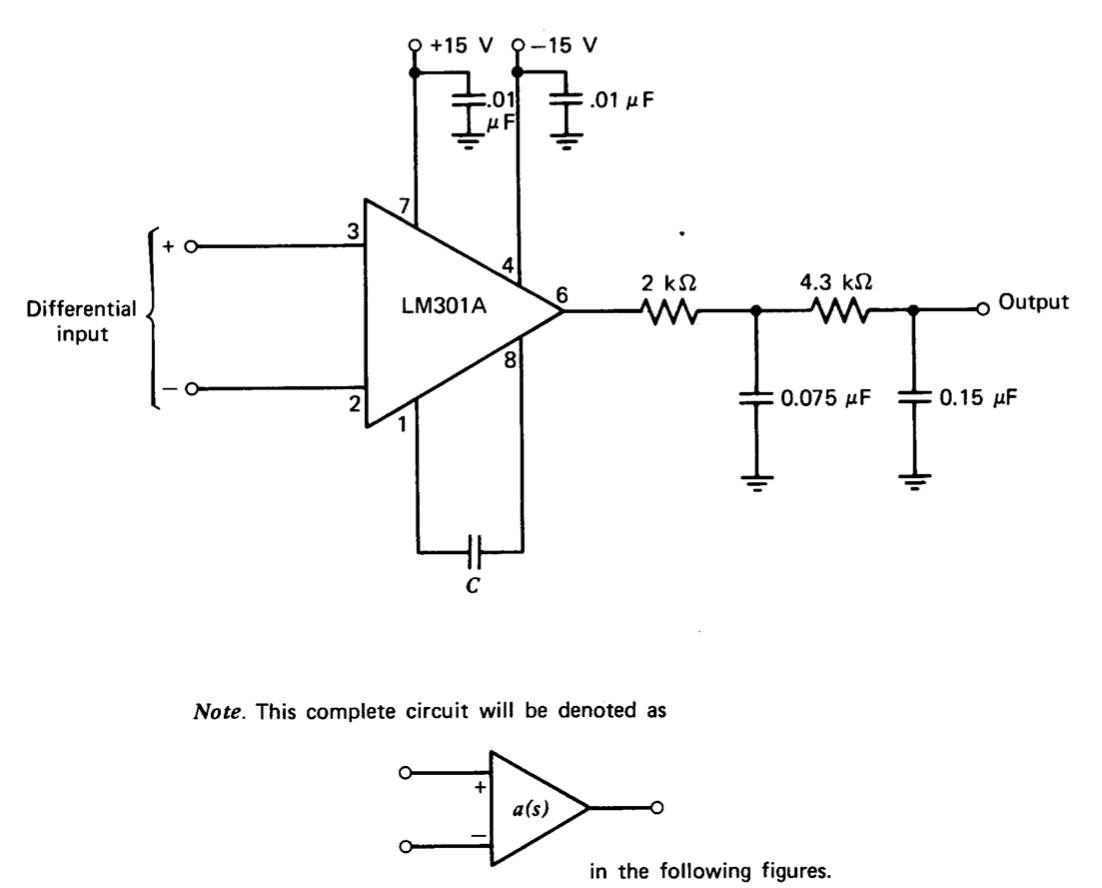
Ця проблема включає в себе лабораторну частину, яка може бути виконана з загальнодоступним випробувальним обладнанням, і це дасть вам досвід компенсації системи з чітко визначеною динамікою. Експериментальним транспортним засобом є схема, показана на малюнку 5.28, яка дає досить повторювані експлуатаційно-підсилювальні характеристики. Запропоновані експерименти використовують конфігурацію на відносно низьких частотах, так що неминучі блукаючі елементи схеми мало впливають на вимірювану продуктивність.

Динаміка схеми спочатку повинна бути стандартизована. Підключіть його як інвертуючий підсилювач, як показано на малюнку 5.29.

Виберіть конденсатор,$C$ підключений між контактами 1 і 8 LM301A, щоб конфігурація була якраз на межі нестабільності. Орієнтовна величина повинна бути близько 5000 пФ. Будь ласка, пам'ятайте, що підсилювач реагує дуже погано (як правило, вмираючи), якщо контакти 1 або 5 закорочені майже на будь-який потенціал.

Примітка. Припущення, необхідні для лінійного аналізу, серйозно порушені, якщо пікова величина вхідного сигналу перевищує приблизно 50 мВ. Також необхідно мати низький опір джерела водіння в цьому та інших з'єднаннях. Запропоновано резистивний дільник, що послаблює вихід генератора сигналів і розташований близько до підсилювача.

Після цієї стандартизації стверджується, що якщо навантаження, що застосовуються до підсилювача, набагато вище вихідного опору мережі за участю конденсатора 0,15$\mu$ F і т.д., ми можемо наблизити$a(s)$ як

$$a(s) \simeq \dfrac{5 \times 10^4}{(s + 1)(10^{-3}s + 1)(10^{-4} s + 1)} \nonumber$$

для цілей аналізу стійкості. Ця передавальна функція не є унікальною і, загалом, функціями форми

$$a(s) = \dfrac{5 \times 10^4 \tau}{(\tau s + 1)(10^{-3} s + 1)(10^{-4} s + 1)} \nonumber$$

дасть еквівалентні результати у вашому аналізі, забезпечуючи$\tau \gg 10^{-3}$ секунди. Наведіть переконливий аргумент, чому вищевказане сімейство передавальних функцій належним чином представляє операційний підсилювач, який ви щойно довели до межі коливань. Зауважте, що простого показу двох заданих виразів є еквівалентними, недостатньо. Ви повинні показати, чому їх можна використовувати для аналізу стандартизованої схеми.

Малюнок 5.30 Інвертуючий підсилювач посилення десяти.

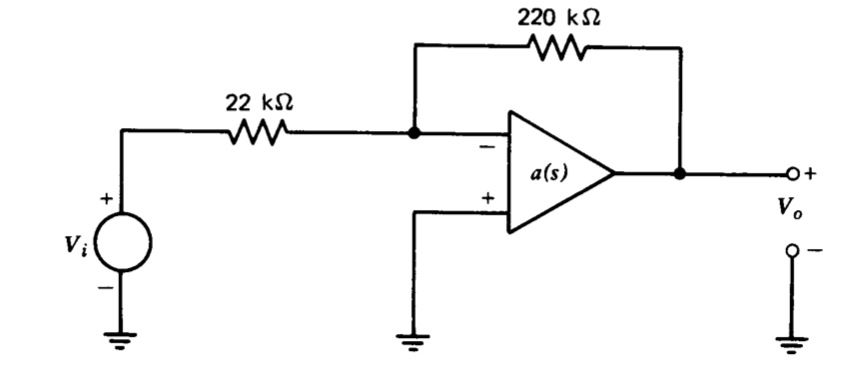
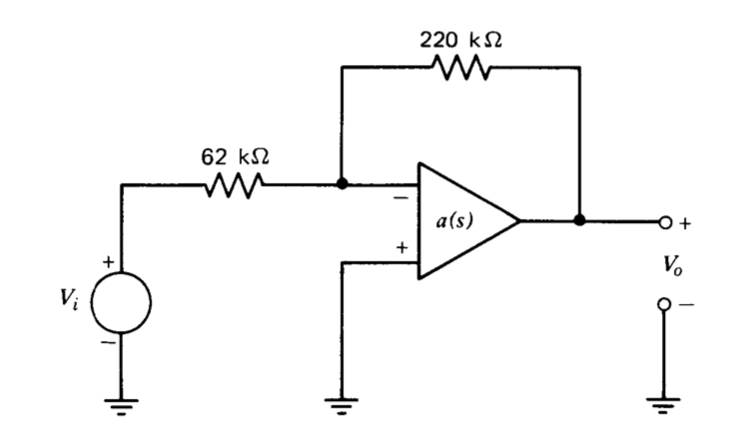
Використовуйте графік Боде для визначення фазового запасу з'єднання, показаного на малюнку 5.30, коли використовується стандартизований підсилювач. Прогнозуйте значення на$M_p$ основі фазового запасу та порівняйте свій прогноз із виміреними результатами.

Ви повинні компенсувати систему, щоб покращити її запас фази$60^{\circ}$ шляхом зменшення$a_0f_0$ та використання методів компенсації відставання та свинцю. Ви не можете змінювати значення$C$ або елементи в мережі, підключені до виходу LM301A, а також необгрунтовано навантажувати мережу для здійснення компенсації.

Аналітично визначте топологію та значення елементів, які ви будете використовувати для кожної з трьох форм компенсації. Можливо, неможливо досягти мети фазового маржі, використовуючи компенсацію свинцю поодинці; якщо ви виявите, що це так, ви можете$a_0f_0$ трохи зменшити, щоб досягти мети проектування.

Компенсуйте підсилювач в лабораторії і переконайтеся, що ступінчасті реакції, які ви вимірюєте, є розумними для систем$60^{\circ}$ з запасом фази. Також співвіднесіть час підйому відповідей з вашими прогнозованими значеннями для частот кросовера.