5.2: Компенсація серії
- Page ID
- 31060
Одним із способів змінити продуктивність системи зворотного зв'язку є зміна функції передачі або шляху прямого посилення, або шляху зворотного зв'язку. Ця методика модифікації послідовного елемента в одноконтурної системі називається послідовною компенсацією. Зміни можуть включати d-c посилення елемента або його динаміки або обох.
Регулювання коефіцієнта посилення D-C
Одна концептуально проста модифікація, яка може бути внесена до передачі петлі, полягає в зміні його значення d-c або середньої смуги\(a_0f_0\). Ця модифікація має прямий вплив на низькочастотну дечутливість, оскільки ми бачили, що ослаблення до змін посилення прямого шляху, що забезпечується зворотним зв'язком, дорівнює\(1 + a_0f_0\).
Динаміка замкнутого циклу також залежить від величини передачі низькочастотного контуру. Приклад з малюнком 4.6 показав, як методи коріння-локус використовуються для визначення взаємозв'язку між\(a_0f_0\) і коефіцієнтом демпфування домінуючої пари полюсів. Другий підхід до управління динамікою замкнутого циклу шляхом коригування\(a_0f_0\) на конкретне значення\(M_p\) був використаний в прикладі з малюнком 4.24.
Припущення, загальне для обох цих попередніх прикладів, полягало в тому, що значення\(a_0f_0\) може бути обрано без зміни особливостей, включених в цикл передачі. Для окремих типів систем зворотного зв'язку незалежність від величини d-c і динаміки контурної передачі реалістична. У динаміці сервомеханізмів, наприклад, зазвичай переважають механічні компоненти з пропускною здатністю менше 100 Гц. Частина передачі контуру d-c сервомеханізму часто забезпечується електронним підсилювачем, і ці підсилювачі можуть забезпечити незалежний від частоти посилення в діапазоні високих кілогерц або мегагерц. Зміна посилення підсилювача змінює значення,\(a_0f_0\) але залишає динаміку, пов'язану з петлею передачі, практично без змін.
Такий тип незалежності часто відсутній в операційних підсилювачах. Для того, щоб збільшити посилення, можливо, доведеться додати етапи, що виробляє значні зміни в динаміці. Зниження коефіцієнта посилення підсилювального каскаду також може змінити динаміку, оскільки, наприклад, залежність між вхідною ємністю та посиленням напруги підсилювача загального випромінювача. Подальша практична складність виникає в тому, що, як правило, не існує передбачуваного способу зміни коефіцієнта посилення розімкнутого контуру d-c наявних дискретних або інтегрованих операційних підсилювачів з наявних клем.
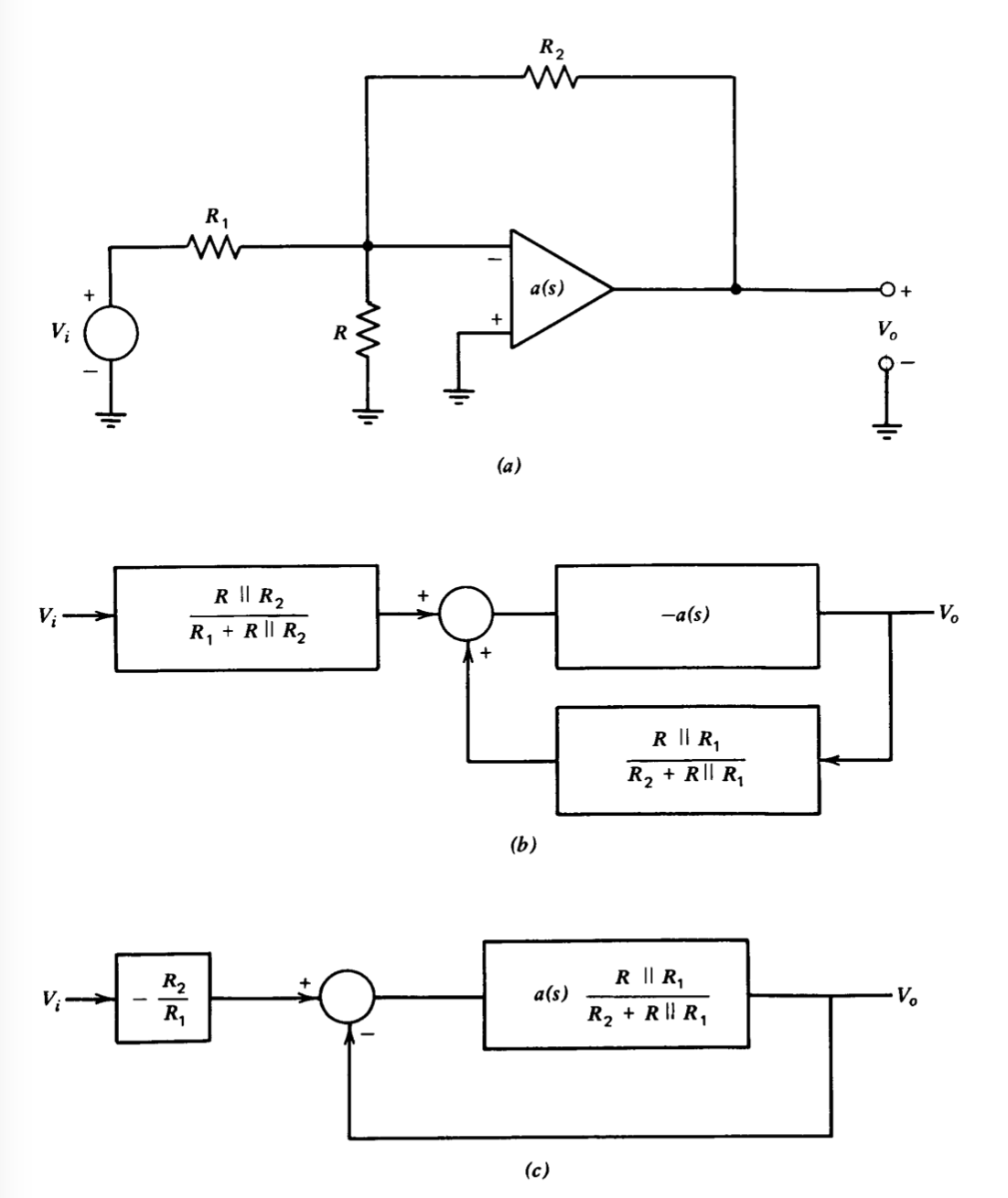
Альтернативний підхід передбачає модифікацію транс-місії d-c петлі за допомогою мережі зворотного зв'язку, підключеної навколо підсилювача. Підключення малюнка 5.1\(a\) ілюструє одну можливість. Блок-схема цього підсилювача, що передбачає незначне навантаження або на вході, або на виході, показана в частині b цього малюнка, тоді як блок-схема після зменшення до форми зворотного зв'язку одиниці показана частково\(c\). Якщо опір шунта\(R\) від інвертуючого входу на землю є розімкнутим контуром, значення d-c контурної передачі повністю визначається\(a_0\) і ідеальним коефіцієнтом посилення замкнутого контуру\(-R_2/R_1\). Однак включення\(R\) забезпечує додатковий ступінь свободи, так що передача петлі d-c і ідеальне посилення можна змінювати самостійно.
Ця методика проілюстрована для інвертора одиничного посилення (\(R_1 = R_2\)) і
\[a(s) = \dfrac{10^6}{(s +1)(10^{-5} s + 1)} \nonumber \]
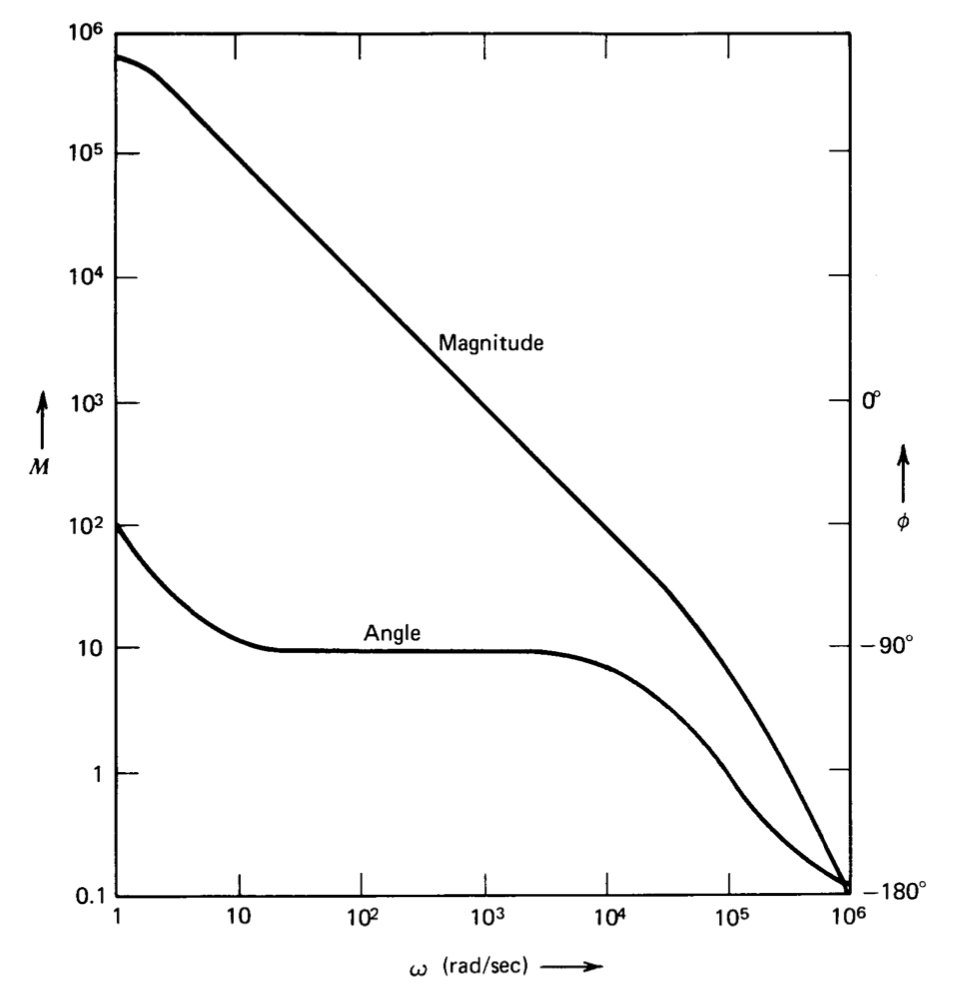
Графік Боде цієї передавальної функції показаний на малюнку 5.2. Якщо обрив ланцюга, то величина передачі контуру\(R\) дорівнює одиниці приблизно\(2.15 \times 10^5\) радіанів в секунду, так як величина\(a(s)\) на цій частоті дорівнює коефіцієнту двох загасань, що забезпечуються\(R_1-R_2\) мережею. Запас фази системи дорівнює\(25^{\circ}\), а на малюнку 4.26\(a\) видно, що коефіцієнт загасання замкнутого контуру дорівнює 0,22. Оскільки малюнок 4.26 був створений, припускаючи цей тип передачі петлі, він дає точні результати в цьому випадку. Якщо резистор\(R\) зроблений рівним\(0.2R_1\), то частота одиниці посилення петлі-передачі знижується до\(10^5\) радіанів в секунду на коефіцієнт семи загасання, що забезпечується мережею, а запас фази і коефіцієнт загасання збільшуються до\(45^{\circ}\) і 0,42 відповідно. Один штраф, сплачений за цей тип ослаблення на вхідних клемах підсилювача, полягає в тому, що зміщення напруги і шум на виході підсилювача збільшені при заданому зміщенні і шумі на вхідних клемах підсилювача (див. Проблема Р5.2).
Створення домінуючого полюса
Елементарні міркування показують, що однополюсна контурна передача призводить до стабільної системи при будь-якій кількості негативного зворотного зв'язку, і що пропускна здатність замкнутого контуру такої системи збільшується зі збільшенням\(a_0f_0\). Аналогічно, якщо передача петлі поблизу частоти посилення одиниці переважає один полюс, достатній запас фази легко отримати. Через простоту стабілізації приблизно однополюсних систем багато типів компенсації істотно зводяться до того, щоб один полюс домінував у передачі петлі.
Один метод грубої сили для того, щоб один полюс домінував петлю транс-місії підсилювача - це просто підключити конденсатор від вузла на шляху сигналу до землі. Якщо використовується досить великий конденсатор, коефіцієнт посилення підсилювача знизиться нижче одного на частоті, де інші полюси підсилювача можна ігнорувати. Очевидним недоліком такого підходу до компенсації є те, що він може різко зменшити пропускну здатність системи із замкнутим циклом.
Система зворотного зв'язку, призначена для утримання значення його вихідної постійної незалежно від порушень, називається регулятором. Оскільки на виході не потрібно відстежувати швидко змінюється вхід, смуга пропускання замкнутого циклу є неважливим параметром. Якщо домінантний полюс включений у вихідну частину регулятора, низькочастотні характеристики цього полюса можуть фактично покращити продуктивність системи шляхом ослаблення порушень навіть за відсутності зворотного зв'язку.
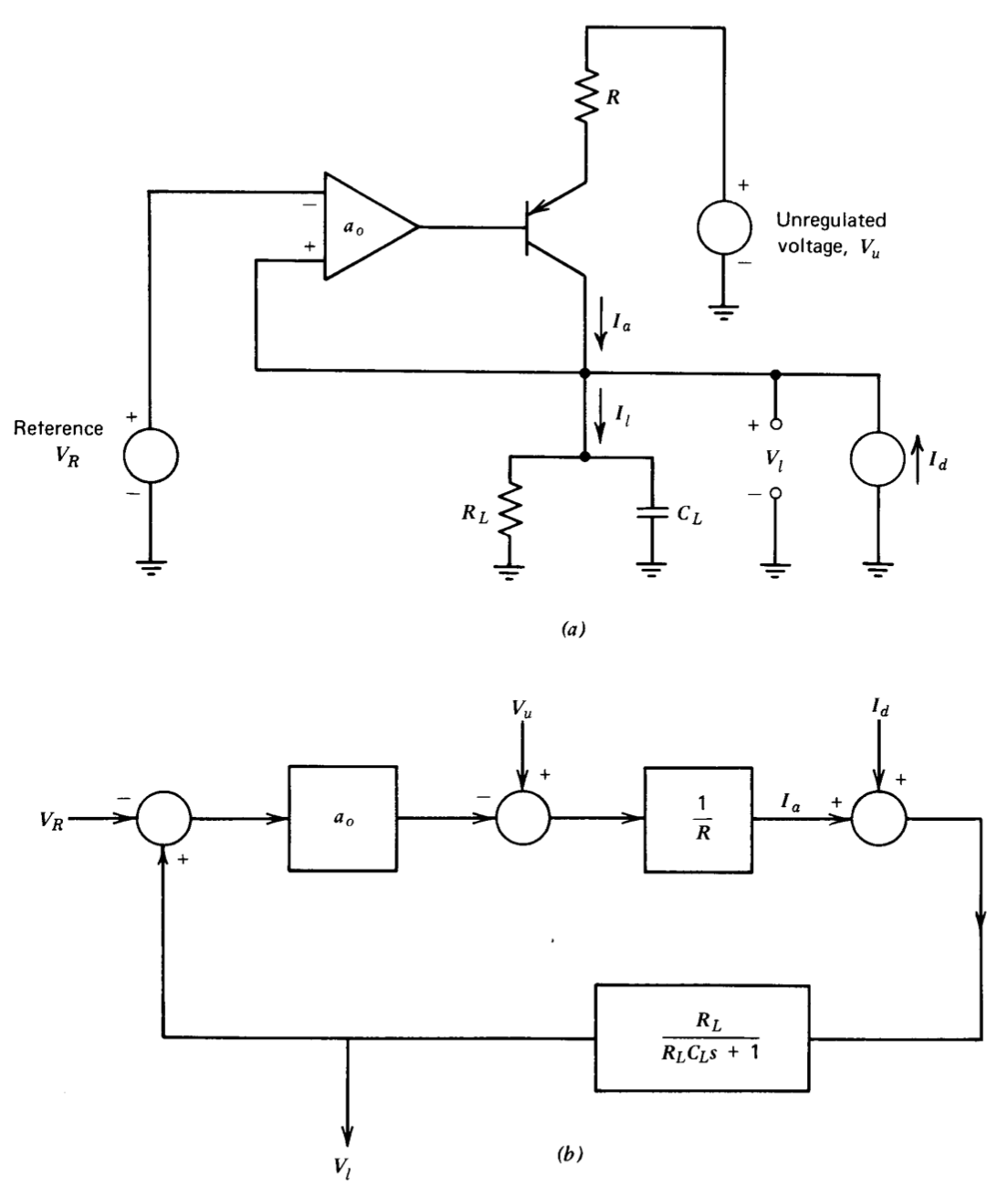
Один з можливих типів стабілізаторів напруги показаний в спрощеному вигляді на малюнку 5.3. Операційний підсилювач використовується для порівняння вихідної напруги з фіксованим еталонним. Операційний підсилювач приводить в рух послідовний каскад регулятора, який складається з транзистора з емітерним резистором. Послідовний регулятор ізолює вихід ланцюга від нерегульованого джерела напруги. Навантаження включає паралельну комбінацію резистор-конденсатор і порушує джерело струму. Джерело струму включається для цілей аналізу і буде використовуватися для визначення ступеня, до якої ланцюг відкидає зміни струму навантаження. Передбачається, що домінантний полюс в системі відбувається через навантаження, і далі передбачається, що операційний підсилювач і послідовний транзистор не сприяють динаміці на частотах, де величина петлі передачі перевищує одиницю.
Блок-схема малюнка 5.3\(b\) моделює регулятор, якщо передбачається, що коефіцієнт посилення струму загальної бази транзистора один і\(R\) що резистор великий в порівнянні з зворотною транзисторної транспровідності. Ця схема перевіряє однополюсний характер передачі петлі системи.
Як вже говорилося раніше, метою схеми є мінімізація змін напруги навантаження, що виникають внаслідок змін тривожного струму і нерегульованого напруги. Функції передачі замкнутого циклу порушення на вихід, які вказують на те, наскільки добре регулятор досягає цієї мети, є
\[\dfrac{V_l}{I_d} = \dfrac{R/a_0}{RC_L s/a_0 + (1 + R/a_0 R_L)} \nonumber \]
і
\[\dfrac{V_l}{V_u} = \dfrac{1/a_0}{RC_L s/a_0 + (1 + R/a_0 R_L)} \nonumber \]
Якщо розглядати синусоїдальні порушення, то величина або функції передачі порушення-вихід є максимальною при d-c, і зменшується зі збільшенням частоти через низькочастотних характеристик навантаження. Збільшення\(C_L\) покращує продуктивність, оскільки знижує частоту, при якій порушення значно послаблюється порівняно з його значенням d-c. Якщо передбачається, що до регулятора можуть бути підключені довільні навантаження (що є звичайною ситуацією, якщо, наприклад, дана схема використовується в якості лабораторного джерела живлення), то значення\(R_L\) і\(C_L\) повинні вважатися змінними. Мінімальне значення\(C_L\) може бути обмежено включенням конденсатора зі схемою регулювання. Значення навантажувального конденсатора збільшується в міру підключення зовнішніх навантажень до регулятора через роз'єднувальних конденсаторів, зазвичай пов'язаних з цими навантаженнями. Аналогічно\(R_L\) зменшується зі збільшенням навантаження до деякого мінімального значення, що визначається обмеженнями навантаження.
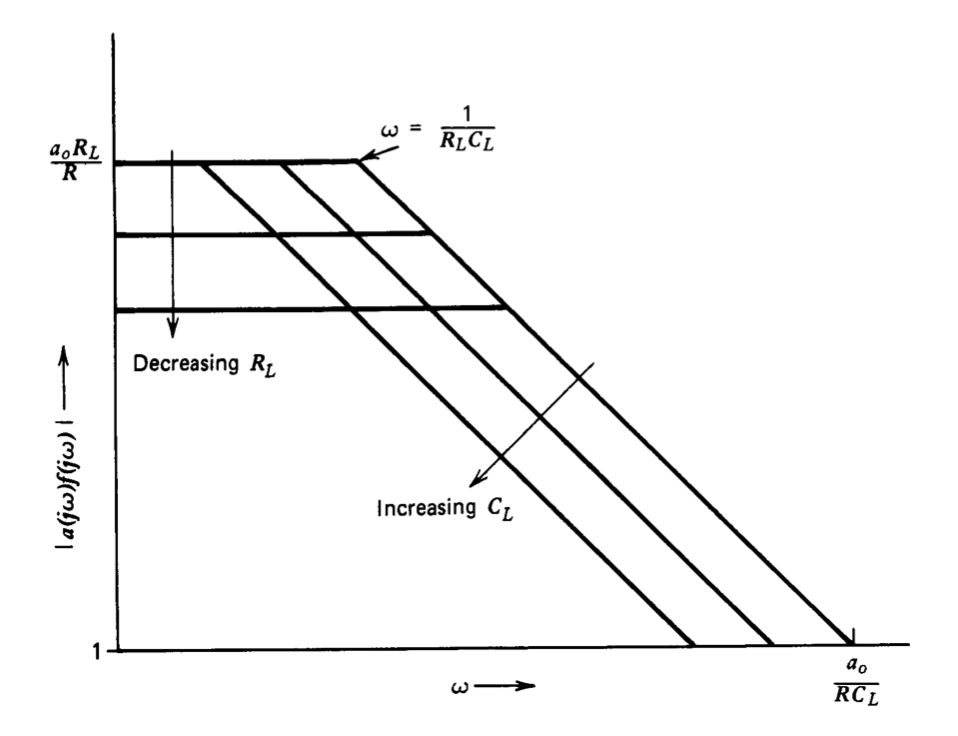
Компенсація, що забезпечується полюсом на виході регулятора, зберігає стабільність у міру\(R_L\) зміни CL, як показано на графіку Боде на малюнку 5.4. (Негатив петлевої передачі для цієї ділянки дорівнює\(a_0R_L/ R(R_LC_Ls + 1)\), визначається безпосередньо з малюнка 5.3\(b\).) Зверніть увагу, що частота одиниці-посилення може бути обмежена обмеженням максимального значення\(a_0/RC_L\) коефіцієнта, і таким чином кросовер може бути змушений до того, як інші елементи системи вплинуть на динаміку. Фазовий запас системи залишається близьким до\(90^{\circ}\) як\(R_L\) і\(C_L\) варіюється в широких межах.
Компенсація свинцю та затримки
Якщо конструктор вільний модифікувати динаміку передачі контуру, а також її низькочастотну величину, він має значно більший контроль над роботою системи із замкнутим циклом. Досить проста модифікація виготовлення однополюсного домінуючого вже обговорювалася.
Види змін, які можуть бути внесені в динаміку петльової передачі, обмежені навіть в чисто математичних системах. Заманливо думати, що системи можна вдосконалити, наприклад, додаючи позитивний зсув фаз до передачі петлі без зміни її величини характеристик. Ця модифікація явно покращила б фазовий запас системи. На жаль, величина і кутові характеристики фізично реалізованих передавальних функцій не є незалежними, а передавальні функції, що забезпечують позитивний зсув фаз, також мають величину, яка збільшується зі збільшенням частоти. Збільшення величини може призвести до більш високої частоти кросовера системи, а додатковий негативний зсув фаз, що виникає в результаті інших елементів петлі, може звести нанівець сподіваються на переваги.
Спосіб реалізації послідовної компенсації та типи компенсаційних передавальних функцій, які можна отримати в практичних системах, ще більше обмежуються апаратними реаліями компенсуваної системи зворотного зв'язку. Конструктор сервомеханізму зазвичай має велику різноманітність доступних йому компенсаційних передавальних функцій, так як електричні мережі і підсилювачі, зазвичай використовувані для компенсації сервомеханізмів, мають практично необмежену пропускну здатність щодо механічних частин системи. І навпаки, ми повинні пам'ятати, що вибір конструктора підсилювача зворотного зв'язку більш обмежений, оскільки способи передачі функції підсилювача можуть бути змінені, особливо поблизу його частоти посилення одиниці, де обмеження пропускної здатності транзистора домінують у продуктивності, часто сильно обмежені. .
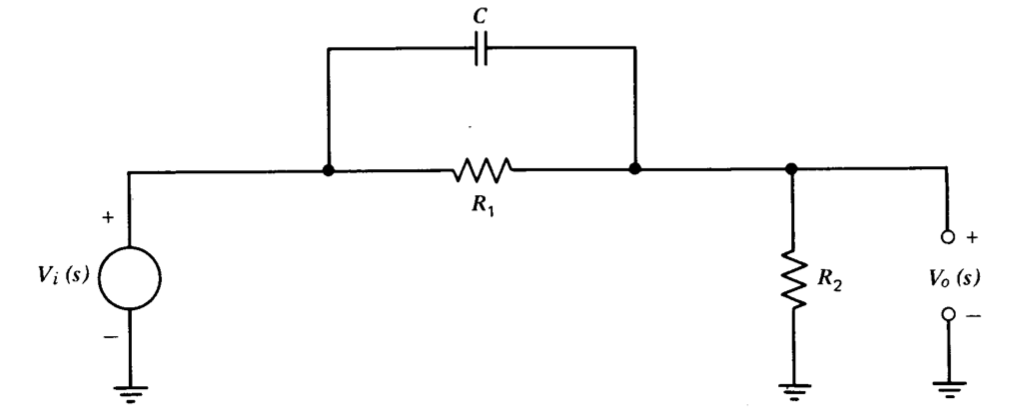
Два різних типи передавальних функцій зазвичай використовуються для послідовної компенсації систем зворотного зв'язку, і ці типи можуть використовуватися або окремо, або можуть бути об'єднані в одній системі. Функцію передачі свинцю можна реалізувати за допомогою мережі, показаної на малюнку 5.5. Передавальна функція цієї мережі:
\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{1}{\alpha} \left [\dfrac{\alpha \tau s + 1}{\tau s + 1} \right ] \nonumber \]
де\(\alpha = (R_1 + R_2)/R_2\) і\(\tau = (R_1 || R_2)C\). Як випливає з назви, ця мережа забезпечує позитивний або провідний зсув фаз вихідного сигналу щодо вхідного сигналу на всіх частотах. Параметри свинцевої мережі зазвичай вибираються, щоб знайти її особливості поблизу частоти кросовера компенсуваної системи. Позитивний зсув фаз мережі потім покращує запас фази системи. У багатьох випадках провідна мережа має незначний вплив на величину характеристики компенсованої системи на частоті кросовера або нижче, оскільки ми побачимо, що провідна мережа забезпечує значний зсув фаз до того, як її величина значно збільшиться.
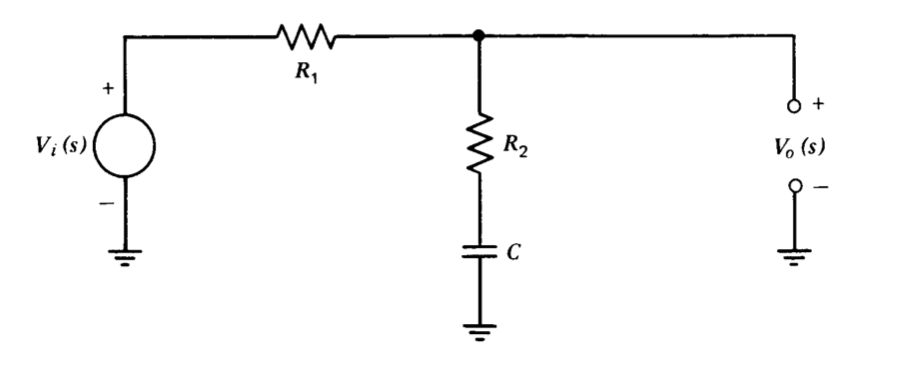
Мережа лаг, показана на малюнку 5.6, має функцію передачі
\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{\tau s + 1}{\alpha \tau s + 1} \nonumber \]
де\(\alpha = (R_1 + R_2)/R_2\) і\(\tau = R_2 C\). Особливості цього типу мережі, як правило, розташовані значно нижче кросовера, щоб зменшити частоту кросовера системи, щоб негативний зсув фаз, пов'язаний з іншими елементами системи, зменшувався на частоті посилення одиниці. Такий ефект можливий через ослаблення лаг-мережі на частотах вище обох її особливостей.
Максимальна величина фазового кута, пов'язаного з будь-якою з цих передавальних функцій, становить
\[\phi_{\max} = \sin^{-1} \left [\dfrac{\alpha - 1}{\alpha + 1} \right ] \nonumber \]
і ця величина виникає при середньогеометричному значенні частот двох сингулярностей. Коефіцієнт посилення будь-якої мережі при максимальній частоті фазового зсуву становить\(1/\sqrt{a}\).
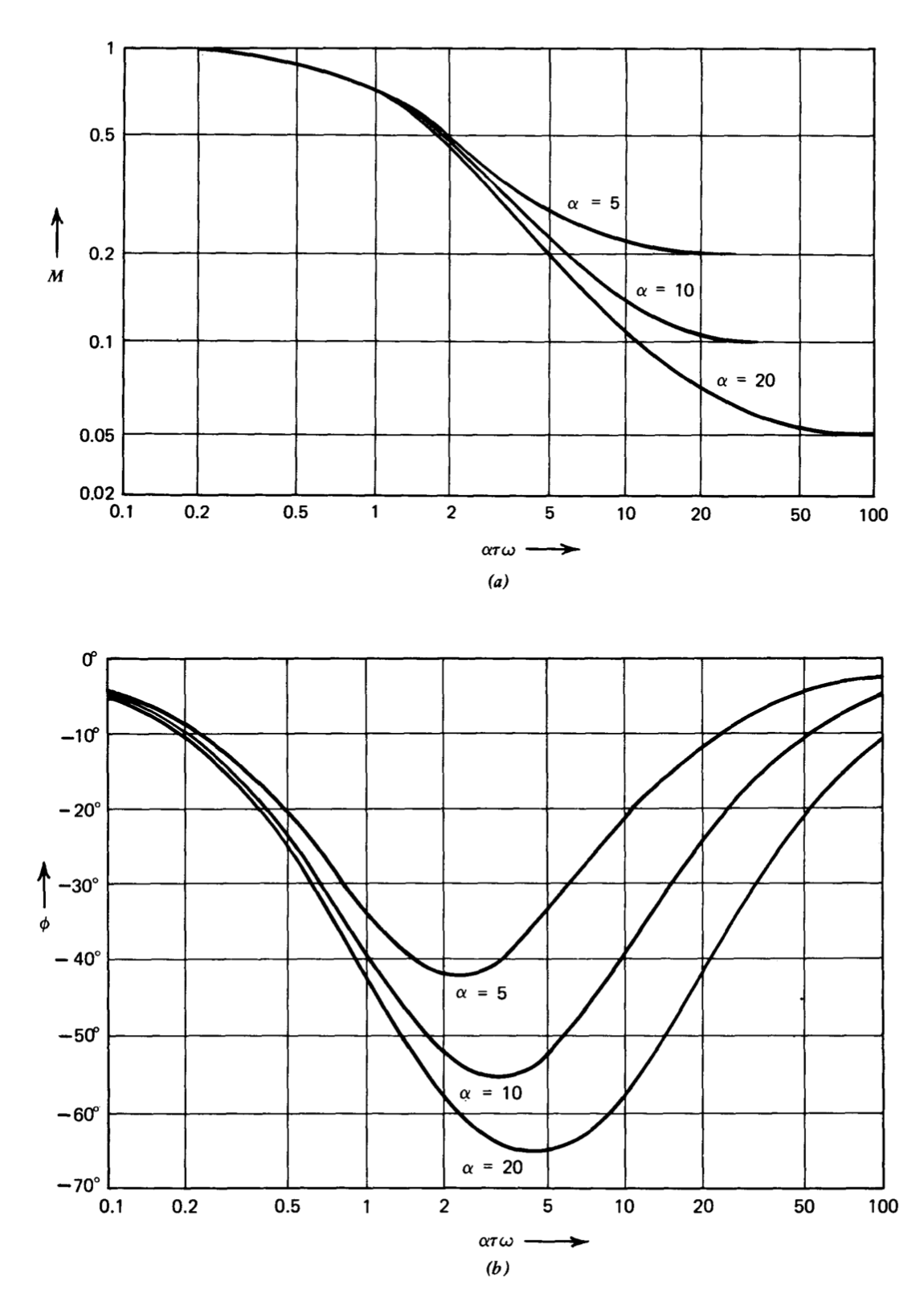
Величини та кути передавальних функцій відведення для\(\alpha\) значень 5, 10 та 20 показані у формі Бод-графіка на малюнку 5.7. На малюнку 5.8 показані відповідні криві для функцій перенесення затримок. Кутові частоти для
полюси побудованих функцій нормалізуються до одного на цих цифрах. Як згадувалося раніше, важливою особливістю функції передачі свинцю є те, що вона забезпечує істотний позитивний зсув фаз в діапазоні частот.
нижче його нульового розташування без значного збільшення величини. Причина випливає з основної властивості реальних осі сингулярностей. На частотах нижче нульового розташування ця сингулярність домінує над функцією передачі свинцю, тому
\[\dfrac{V_o (s)}{V_i (s)} \simeq \dfrac{1}{\alpha} (\alpha \tau s + 1) \nonumber \]
Величина і кут цієї функції
\[M = \dfrac{1}{\alpha} [\sqrt{1 + (\alpha \tau \omega)^2}] \nonumber \]
\[\phi = \tan^{-1} \alpha \tau \omega \nonumber \]
При невеликій частці нульового розташування\(\alpha \tau \omega \ll 1\), так
\[M \simeq \dfrac{1}{\alpha} \left [1 + \dfrac{(\alpha \tau \omega)^2}{2} \right ] \nonumber \]
\[\phi \simeq \alpha \tau \omega \nonumber \]
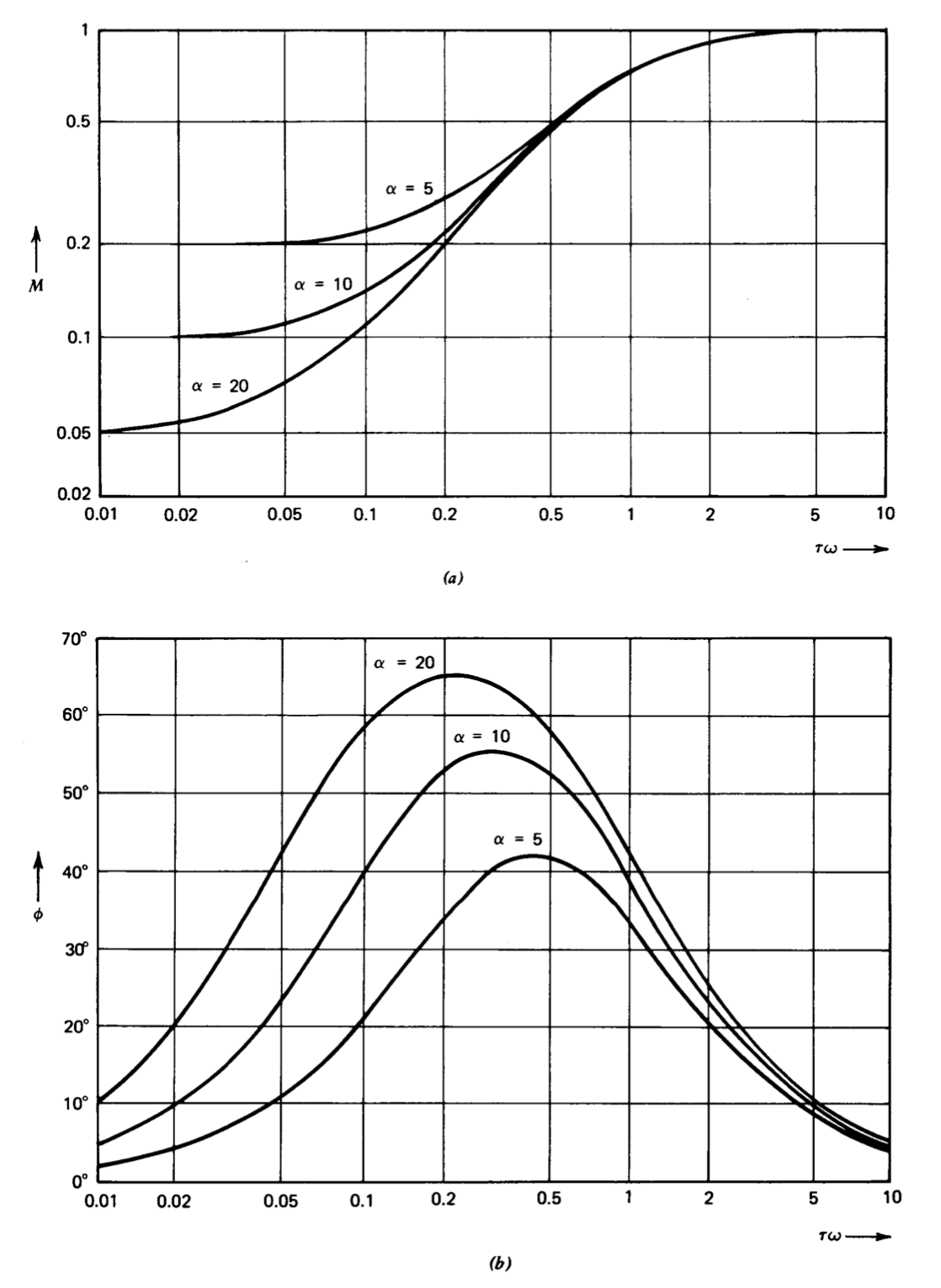
Оскільки кут зростає лінійно з частотою в цій області, тоді як величина збільшується квадратично, зміна кута відносно більша при заданій частоті. Таке ж міркування застосовується навіть в тому випадку, якщо нуль розташований на кросовері або трохи нижче. На малюнку 5.7 показано, що позитивний зсув фаз відведення передавальної функції при розумному значенні\(\alpha\) знаходиться приблизно\(40^{\circ}\) в його нульовому місці, тоді як збільшення величини становить лише коефіцієнт 1,4. Значна частина цієї переваги втрачається на частотах, що перевищують середнє геометричне особливості, оскільки позитивний зсув фаз зменшується за межі цієї частоти, тоді як величина продовжує зростати.
Слід визнати, що ізольований нуль може бути використаний замість функції передачі відведення, і що цей тип передавальної функції насправді має характеристики фазового зсуву, що перевершують характеристики пари нульового полюса. Однак необмежене посилення високих частот, що мається на увазі ізольованим нулем, явно недосяжний, принаймні на досить високих частотах. Таким чином, введена раніше форма функції перенесення свинцю відображає реалії фізичних систем.
Важливою особливістю функції перенесення затримки, проілюстрованої на малюнку 5.8, є те, що на частотах значно вище нульового розташування вона забезпечує загасання величини, рівне співвідношенню двох місць сингулярності та незначного зсуву фаз. Таким чином, він може бути використаний для зменшення величини петлі транс-місії без суттєвого додавання до негативного зсуву фаз цієї передачі на помірних частотах.
Приклад
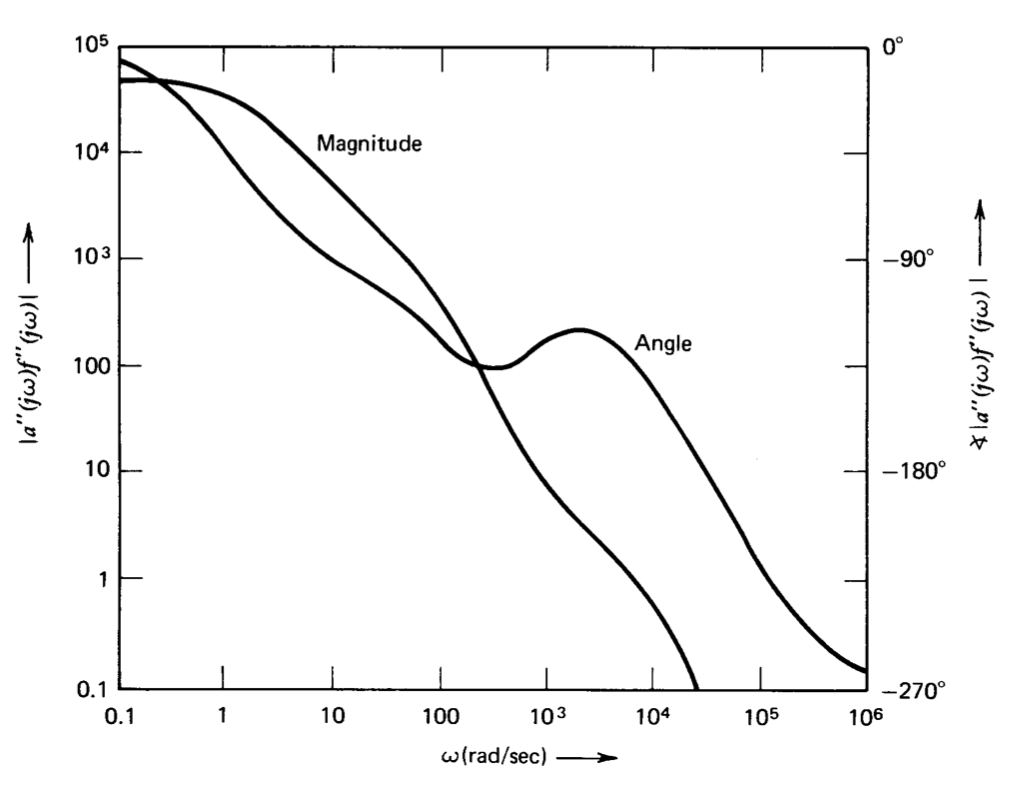
Свинцеві та лаг-мережі спочатку були розроблені для використання в сервомехічних анізмах і забезпечують потужний засіб компенсації, коли їх особливості можуть бути розташовані довільно по відношенню до інших полюсів системи і коли можливо незалежне регулювання величини низькочастотної петлі-передачі. Навіть без цієї гнучкості, яка зазвичай відсутня в схемах операційного підсилювача, компенсація відведення або затримки може забезпечити ефективний контроль продуктивності замкнутого циклу в певних конфігураціях. Як приклад розглянемо неінвертирующее підключення підсилювача посилення десяти, показане на малюнку 5.9. Передбачається, що вхідний і вихідний опір операційного підсилювача невеликі. Функція передачі з відкритим контуром операційного підсилювача є (Хоча аналітичний вираз використовується для\(a(s)\) цього прикладу, читач повинен розуміти, що функція передачі з відкритим контуром операційного підсилювача, як правило, не буде доступна в цій формі. Однак зауважте, що експериментально визначений сюжет Боде цілком прийнятний для всіх необхідних маніпуляцій, і що цю інформацію завжди можна визначити. Загальні характеристики передбачуваної передавальної функції розімкнутого контуру характерні для багатьох операційних підсилювачів, в тому, що в цій величині переважає один полюс на низьких частотах. На частотах, ближчих до частоти посилення одиниці, додатковий негативний зсув фаз виникає внаслідок ефектів, пов'язаних з обмеженнями транзисторів. Як ми побачимо в наступних розділах, ці ефекти обмежують кінцеві можливості підсилювача.)
\[a(s) = \dfrac{5 \times 10^5}{(s + 1)(10^{-4} s + 1) (10^{-5} s + 1)} \nonumber \]
і передбачається, що користувач не може змінити цю функцію. При підключенні, як показано на малюнку 5.9, значення\(f\) дорівнює 0,1, і, таким чином, мінус петлі передачі дорівнює
\[a(s)f(s) = \dfrac{5 \times 10^4}{(s + 1)(10^{-4} s + 1) (10^{-5} s + 1)}\label{eq5.2.11} \]
Коефіцієнт посилення із замкнутим контуром дорівнює
\[\begin{array} {rcl} {\dfrac{V_o (s)}{V_i (s)} = A(s)} & = & {\dfrac{a(s)}{1 + a(s) f(s)}} \\ {} & \simeq & {\dfrac{10}{2 \times 10^{-14} s^3 + 2.2 \times 10^{-9} s^2 + 2 \times 10^{-5} s + 1}} \end{array} \nonumber \]
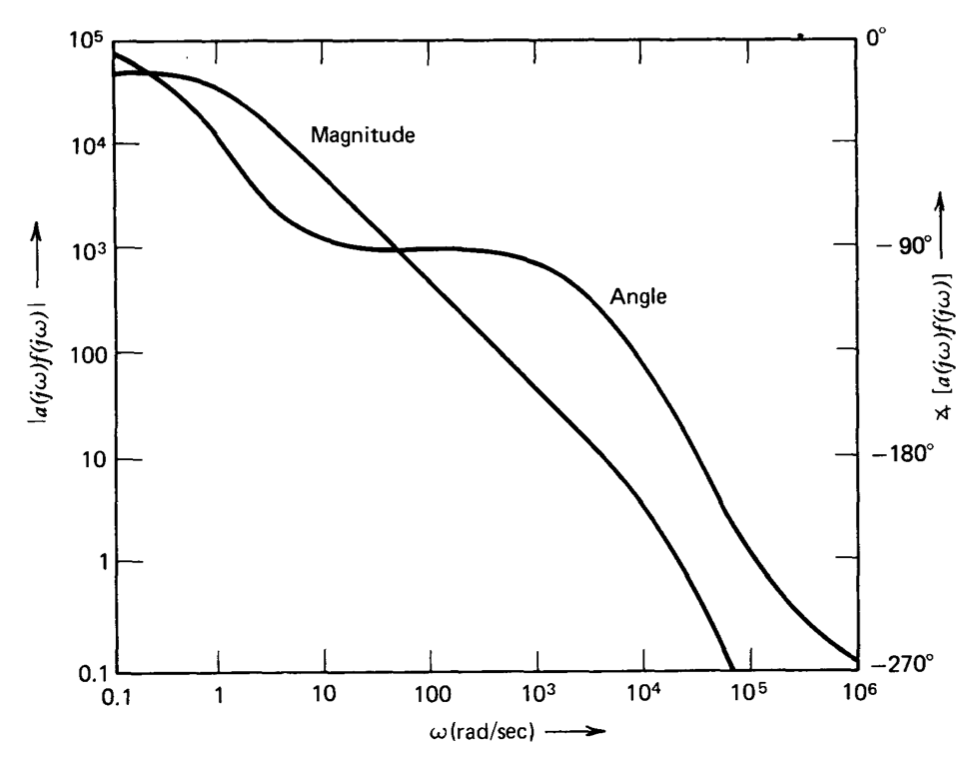
Графік Боде рівняння\(\ref{eq5.2.11}\) (рис. 5.10) показує, що частота кросовера системи -\(2.1 \times 10^4\) радіани в секунду, її фазовий запас -\(13^{\circ}\), а запас посилення - 2.
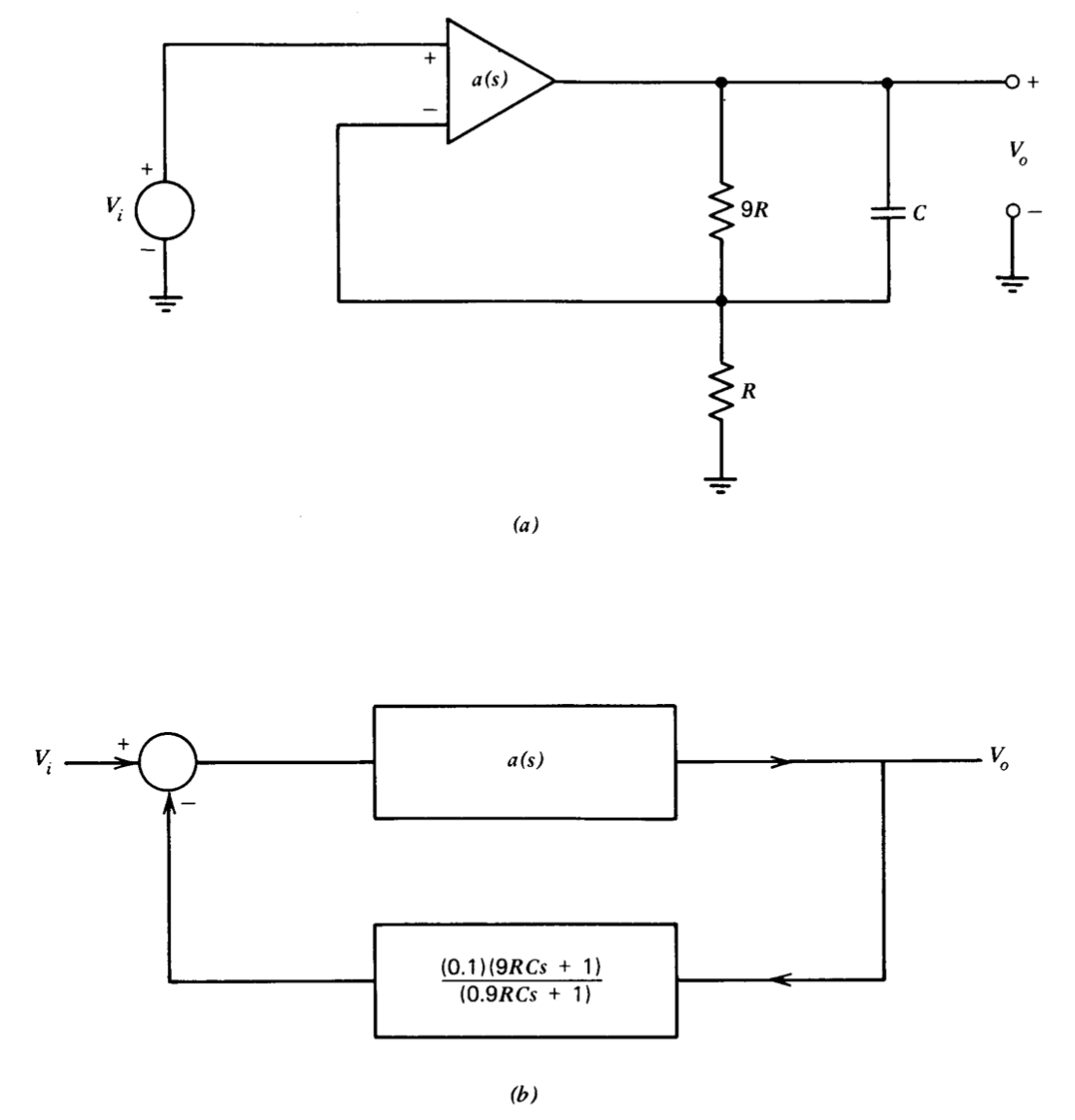
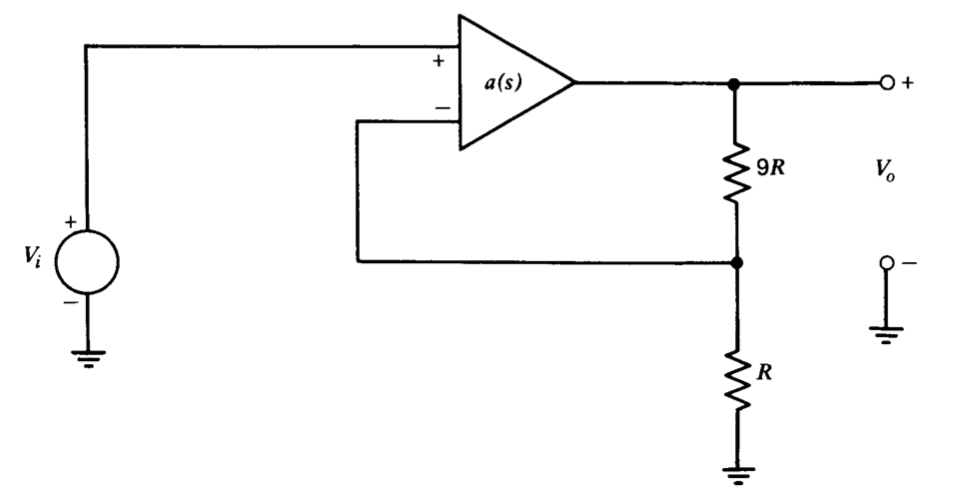
Хоча постановка проблеми виключає зміну\(a(s)\), ми можемо ввести функцію передачі свинцю в петлю передачі, включивши конденсатор через верхній резистор у мережі зворотного зв'язку. Топологія показана на малюнку 5.11\(a\), при цьому блок-схема показана на малюнку 5.11\(b\). Негативним від контурної передачі для системи є
\[a'(s) f'(s) = \dfrac{5 \times 10^4 (9RCs + 1)}{(s + 1)(10^{-4}s + 1)(10^{-5} s + 1)(0.9 RCs + 1)}\label{eq5.2.13} \]
Кілька міркувань впливають на вибір\(R-C\) продукту, який визначає особливості провідної мережі. Як уже згадувалося раніше, метою провідної мережі є забезпечення позитивного зсуву фаз поблизу частоти кросовера, і максимальний позитивний зсув фаз від мережі результатів, якщо кросовер відбувається на середньому геометричному нульовому полюсі пари. Однак особливості мережі і кросовер часто не можуть бути налаштовані самостійно для цієї системи, так як якщо нуль провідної мережі розташований на частоті нижче приблизно\(3 \times 10^4\) радіанів в секунду, частота кросовера збільшується. Збільшення частоти кросовера збільшує негативний зсув фаз підсилювача на цій частоті, компенсуючи частково позитивний зсув фаз мережі. Відповідний розгляд передбачає вплив провідної мережі на ідеальне посилення підсилювача із замкнутим контуром, оскільки мережа введена в шлях зворотного зв'язку, а ідеальне посилення взаємно пов'язане з функцією передачі зворотного зв'язку. Якщо нуль свинцевої мережі розташований на низькій частоті, призводить низькочастотний замкнутий полюс, який зменшує пропускну здатність системи із замкнутим контуром.
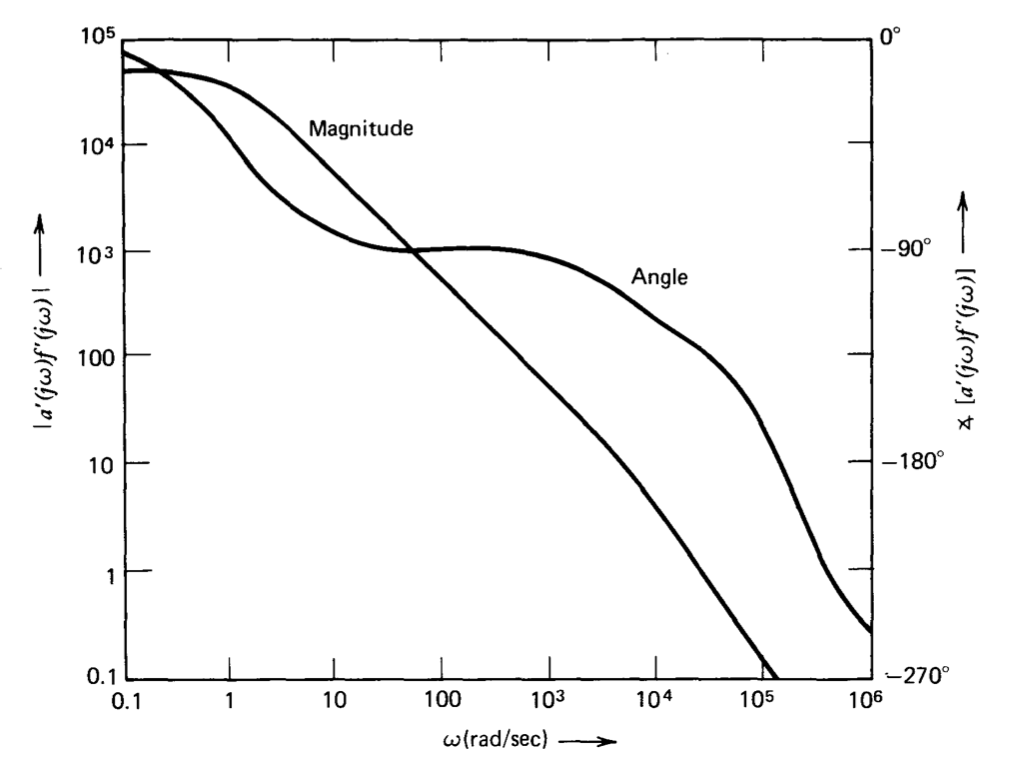
Розумним компромісом в даному випадку є розташування нуля провідної мережі поблизу одиничної частоти посилення, в спробі отримати позитивний зсув фаз від мережі без значного збільшення частоти кросовера. Вибір\(RC = 4.44 \times 10^{-6}\) секунд знаходить нуль при\(2.5 \times 10^4\) радіанах в секунду. Графік Боде рівняння\(\ref{eq5.2.13}\) для цього значення RC показаний на малюнку 5.12. Частота посилення одиниці трохи збільшується до\(2.5 \times 10^4\) радіанів в секунду, тоді як запас фази збільшується до респектабельного значення\(47^{\circ}\). Приріст маржі дорівнює 14.
Функція перенесення затримки може бути введена в прямий шлях підсилювача, шунтуючи послідовну мережу резистор-конденсатор між його вхідними клемами, як показано на малюнку 5.13\(a\). Відзначимо, що таку ж петлю передачі можна було б отримати шунтуванням R-значного резистора з\(R_1 -C\) мережею, так як і нижній кінець\(R\) -значного резистора, і неінвертирующий вхід підсилювача підключені до поступово заземлених точок. Якщо цей параметр пізніше використовувався,\(R_1-C\) мережа ввела б функцію передачі затримки в шлях зворотного зв'язку топології. Отже, ідеальна функція передачі із замкнутим циклом включала б зворотну функцію відставання. Оскільки особливості лаг-мереж, як правило, розташовані на низьких частотах, функція передачі замкнутого циклу може негативно впливати на цікаві частоти. (Див. Проблема P5.7.)
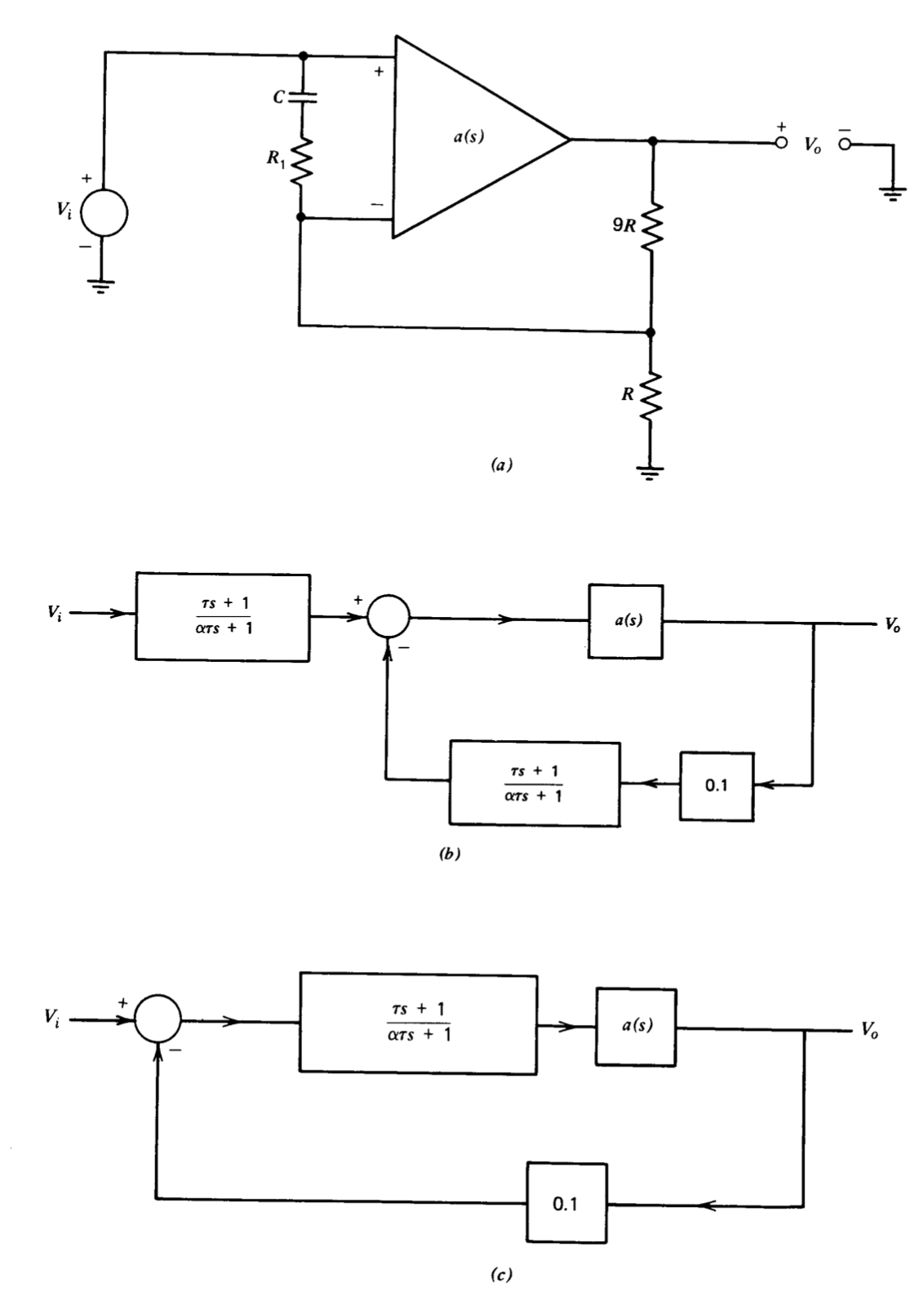
Структурна схема системи для топології малюнка 5.13\(a\) показана на малюнку 5.13\(b\). У цьому випадку функція перенесення лаг з'являється як на шляху зворотного зв'язку, так і на прямому шляху поза циклом. Блок-схему можна переставити, як показано на малюнку 5.13\(c\); і ця остаточна схема показує, що включення\(R_1-C\) мережі між входами підсилювача залишає ідеальне посилення замкнутого контуру без змін. Негативна петля передачі для малюнка 5.13\(c\) дорівнює
\[a''(s) f''(s) = 0.1 \dfrac{(\tau s + 1)}{(\alpha \tau s + 1)} a(s) \nonumber \]
де
\[\alpha = \dfrac{R_1 + 0.9 R}{R_1} \text{ and } \tau = R_1 C\nonumber \]
Як згадувалося раніше, особливості функції передачі відставання, як правило, розташовані значно нижче частоти кросовера системи, так що мережа затримок не погіршує запас фази значно. Часто використовуване правило передбачає розміщення нуля мережі затримки на одній десятій частоті кросовера, що призводить до компенсації, оскільки це значення дає максимальний негативний внесок фази\(5.7^{\circ}\) від мережі на кросовері. Ми також, досить довільно, вирішуємо вибрати параметри lag-мережі, щоб отримати фазовий запас приблизно\(47^{\circ}\), такого ж значення, як і у системи, компенсованої провідною мережею. Графік Боде системи без компенсації, рис. 5.10, допомагає у виборі параметрів лаг-мережі. Ця ділянка вказує на некомпенсований фазовий кут\(-128^{\circ}\) і некомпенсовану величину 6,2 при частоті\(6.7 \times 10^3\) радіанів в секунду. Якщо значення 6,2 є обраним високочастотним загасанням a лаг-мережі, то компенсована частота кросовера становитиме\(6.7 \times 10^3\) радіани в секунду. \(5^{\circ}\)Від'ємний фазовий зсув, очікуваний від правильно розташованої мережі відставання, поєднується з фазовим зсувом системи до компенсації, щоб отримати компенсований запас фази\(47^{\circ}\).\(- 128^{\circ}\) Нуль лаг-мережі розташований на\(6.7 \times 10^2\) радіанах в секунду, коефіцієнт на 10 нижче кросовера. Ці цілі проектування виконуються з\(R_1 = 0.173R\) і\(R_1C = 1.5 \times 10^{-3}\) секундами. При цих значеннях негатив петлевої передачі дорівнює
\[a''(s) f''(s) = \dfrac{5 \times 10^4 (1.5 \times 10^{-3} s + 1)}{(s + 1)(10^{-4} s + 1)(10^{-5} s + 1)(9.3 \times 10^{-3} s + 1)} \nonumber \]
Ця передавальна функція, побудована на малюнку 5.14, вказує на прогнозовані значення частоти кросовера і запасу фази. Маржа посилення становить 15.
Дві інші модифікації передачі петлі призводять до графіків Боде, які схожі на графіки системи з компенсацією затримки поблизу частоти кросовера. Однією з можливостей є зниження значення\(a_0f_0\) в 6,2 рази (див. Розділ 5.2.1). Необхідне зменшення може бути досягнуто простим використанням значення шунт-резистора, визначеного для компенсації затримки безпосередньо через вхідні клеми операційного підсилювача. Ця модифікація призводить до тієї ж частоти кросовера, що і у підсилювача з відставанням, і має на кілька градусів більше запасу фази, оскільки він не має незначного негативного зсуву фаз, пов'язаного з відставанням мережі на кросовері. На жаль, зниження\(a_0f_0\) призводить до більш низького значення дечутливості порівняно з показником підсилювача з відставанням на всіх частотах нижче нуля мережі.
Друга можливість полягає в тому, щоб перемістити нижчечастотний полюс петлевої передачі назад в 6,2 рази. Ця модифікація може бути внесена до самого підсилювача, або може бути здійснена відповідним вибором компонентів лаг-мережі. Вплив на параметри в околицях кросовера по суті ідентичний впливу знижувального\(a_0f_0\). При цьому методі дечутливість зберігається при d-c, але знижується на проміжних частотах порівняно з частотами, що забезпечуються компенсацією затримки. Ці два підходи до компенсації підсилювача, описані тут, детально досліджені в Задачі Р5.8.
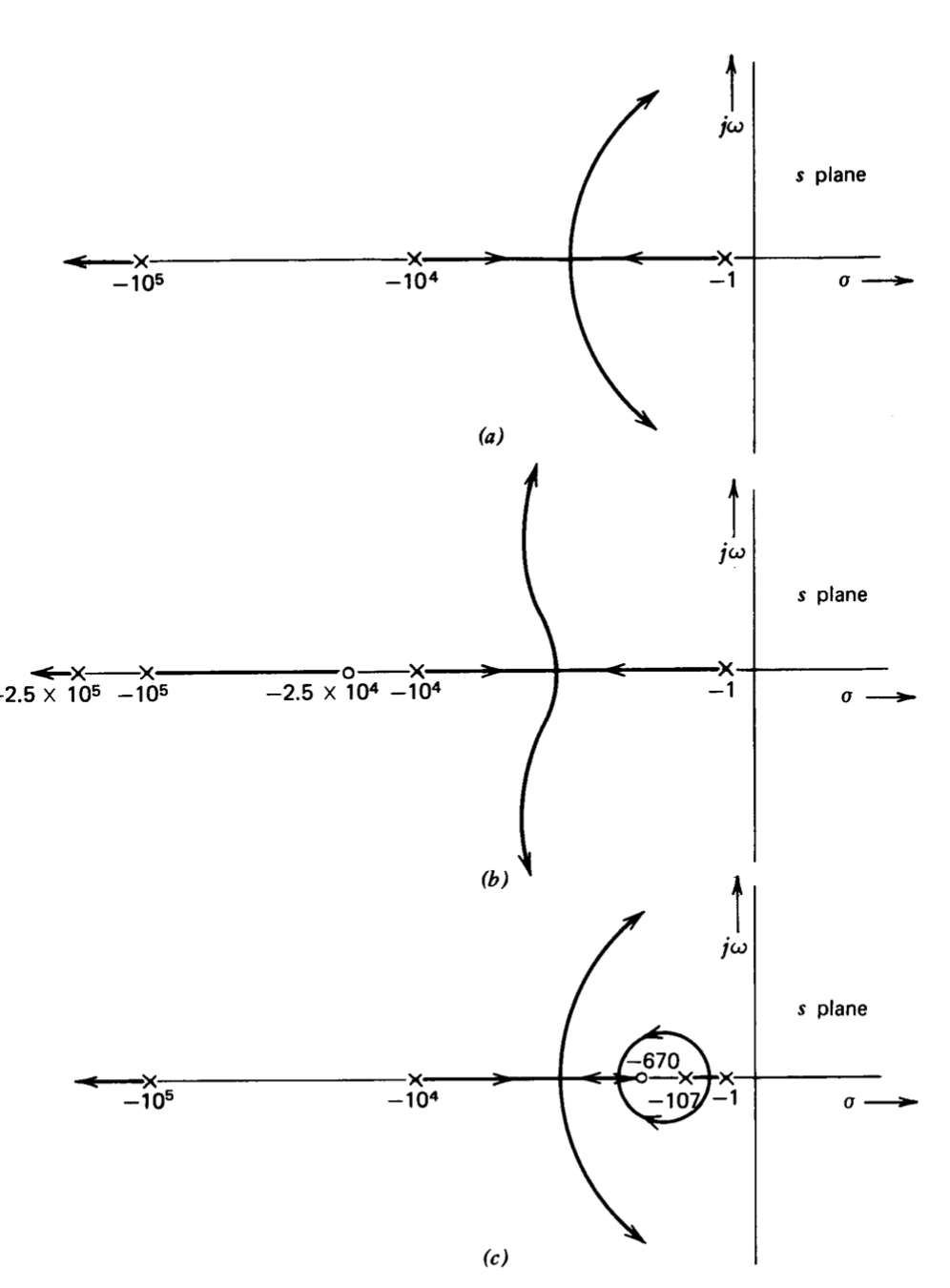
Обговорення компенсації серій до цього моменту було зосереджено на використанні концепцій частотної області фазового запасу, запасу посилення та частоти кросовера для визначення параметрів компенсаційної мережі. Методи кореневого локусу не можуть бути використані безпосередньо,\(a_0f_0\) оскільки значення не змінюється для компенсації ефекту. Однак ескізи кореневого локусу для некомпенсованих, свинець компенсованих та компенсованих відставанням систем, показаних на малюнку 5.15, дають певний ступінь розуміння поведінки системи. (У цих ескізах є значні спотворення, оскільки незручно точно представляти ескізи там, де особливості розташовані на відстані декількох десятиліть один від одного.)
Діаграма кореня-локуса на малюнку 5.15\(a\) ілюструє зміну розташування полюсів із замкнутим контуром як функція\(a_0f_0\) для некомпенсованої системи. Додавання свинцевої мережі (рис. 5.15\(b\)) зміщує домінуючі гілки вліво і, таким чином, покращує демпферний коефіцієнт цієї пари полюсів при заданому значенні\(a_0f_0\).
Ефект компенсації відставання дещо тонший. Діаграма корінь-локус на рис. 5.15\(c\) практично ідентична малюнку 5.15\(a\) за винятком безпосередньої близькості від пари сингулярності лаг-мережа. Однак розрахунок коефіцієнта посилення за допомогою правила 8 (Розділ 4.3.1) показує, що значення,\(a_0f_0\) необхідне для досягнення заданого коефіцієнта демпфування для домінуючої пари, вище приблизно на коефіцієнт a, коли включена мережа відставання.
Кореневі контури також можуть бути використані для показу ефектів зміни одного параметра або мережі відставання. Цей підхід до проектування досліджено в задачах Р5.9 та Р5.10.
Оцінка наслідків компенсації
Існує кілька способів продемонструвати поліпшення продуктивності, що забезпечується компенсацією. Оскільки параметри компенсуючої передавальної функції зазвичай визначаються за допомогою петельно-передавальних графіків Боде, одним простим способом оцінки різних видів компенсації є порівняння отриманої від них дечутливості. Міркування, що використовуються для визначення параметрів свинцевої та лаг-компенсації для операційного підсилювача, підключеного для забезпечення посилення 10, були детально описані в розділі 5.2.4. Отримані петлеві передачі, повторені тут для зручності, є
\[a'(s) f'(s) = \dfrac{5 \times 10^4 (4 \times 10^{-5} s + 1)}{(s + 1)(10^{-4} s + 1)(10^{-5} s + 1)(4 \times 10^{-6} s + 1)}\label{eq5.2.16} \]
і
\[a''(s) f''(s) = \dfrac{5 \times 10^4 (1.5 \times 10^{-3} s + 1)}{(s + 1)(10^{-4} s + 1)(10^{-5} s + 1)(9.3 \times 10^{-3} s + 1)}\label{eq5.2.17} \]
для свинцево- і лаг-компенсованих випадків відповідно. Фаза-запас, отриманий будь-яким методом, приблизно\(47^{\circ}\).
Згадувалося, що стабільність некомпенсованого підсилювача може бути покращена або\(a_0f_0\) зниженням в 6,2 рази, в результаті чого
\[a''' (s) f(s)''' = \dfrac{8.1 \times 10^3}{(s + 1)(10^{-4} s + 1)(10^{-5} s + 1)} \nonumber \]
або знизивши розташування першого полюса на той же коефіцієнт, поступаючись
\[a'''' (s) f''''(s) = \dfrac{5 \times 10^4}{(6.2 s + 1)(10^{-4} s + 1)(10^{-5} s + 1)} \nonumber \]
Будь-який із цих підходів призводить до частоти кросовера, ідентичної частоті системи, що компенсується затримкою, і запас фази приблизно\(52^{\circ}\).
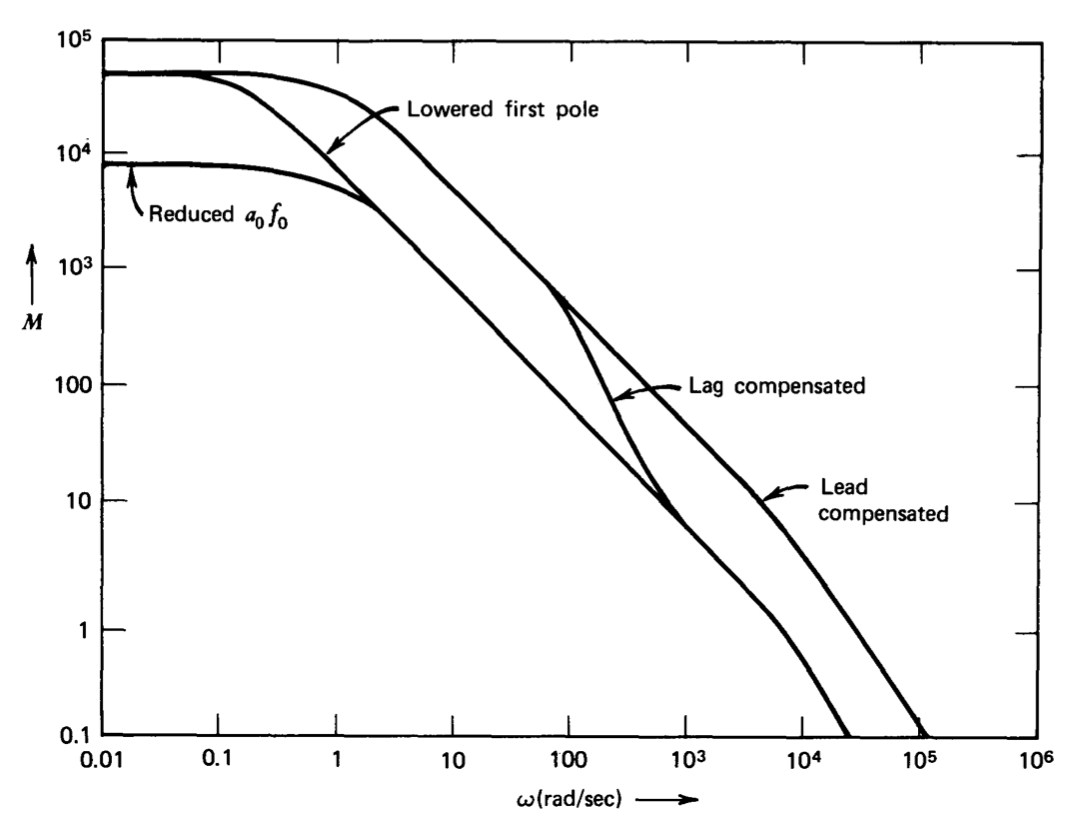
Величина частин петлевих передач для цих чотирьох випадків порівнюється на малюнку 5.16. Відносні дечутливості, які досягаються на різних частотах, а також відносні частоти кросовера очевидні на цій цифрі.
Альтернативним способом оцінки різних методів компенсації є порівняння коефіцієнтів похибки, які отримані з їх допомогою. Цей підхід досліджено в задачі Р5.11. Як і очікувалося, системи з більшою дечутливістю зазвичай також мають коефіцієнти похибки меншої величини.
Обговорення компенсації досі зосереджувалося на використанні графіків Боде, оскільки це, як правило, найшвидший спосіб знайти компенсуючі параметри. Однак цілі проектування часто заявляються з точки зору перехідної реакції, і недосвідчений дизайнер часто відчуває, що акт віри необхідний, щоб прийняти принцип, що системи з правильно підібраними значеннями для фазового запасу, запасу посилення та частоти кросовера будуть виробляти задовільний перехідний відповіді. Відповіді на крок, показані на малюнку 5.17, пропонуються як допомога для встановлення цієї необхідної віри.
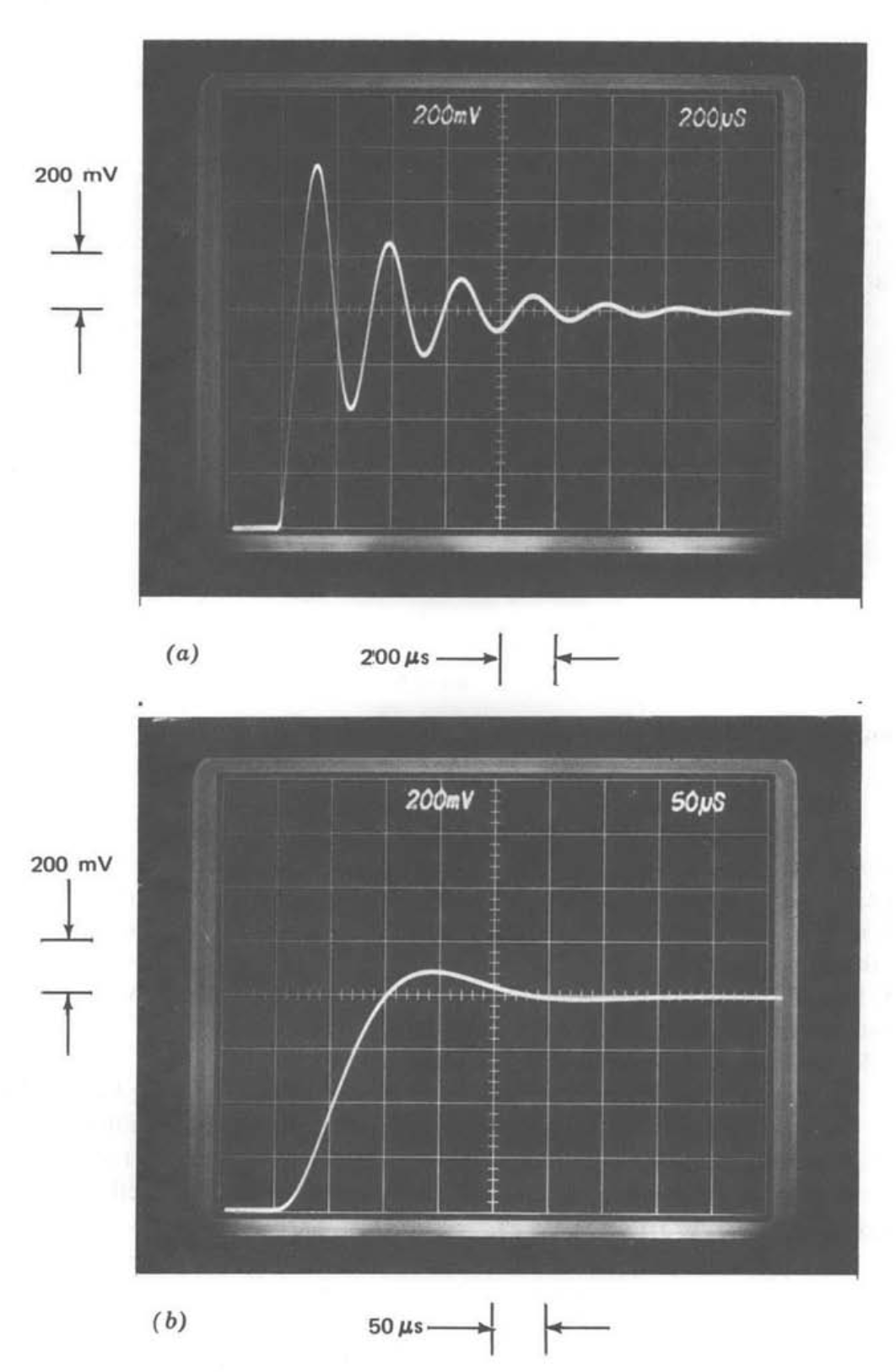
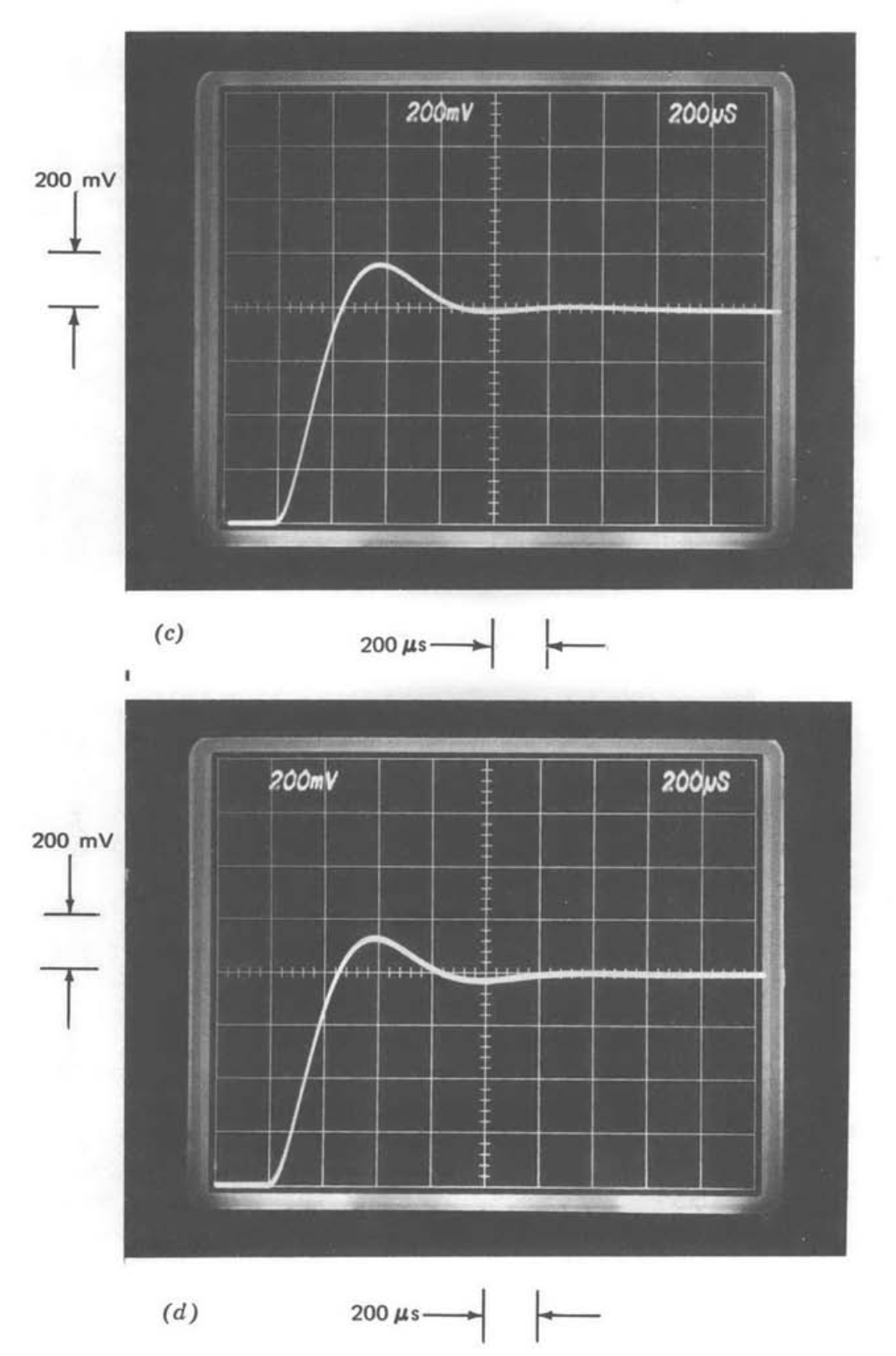
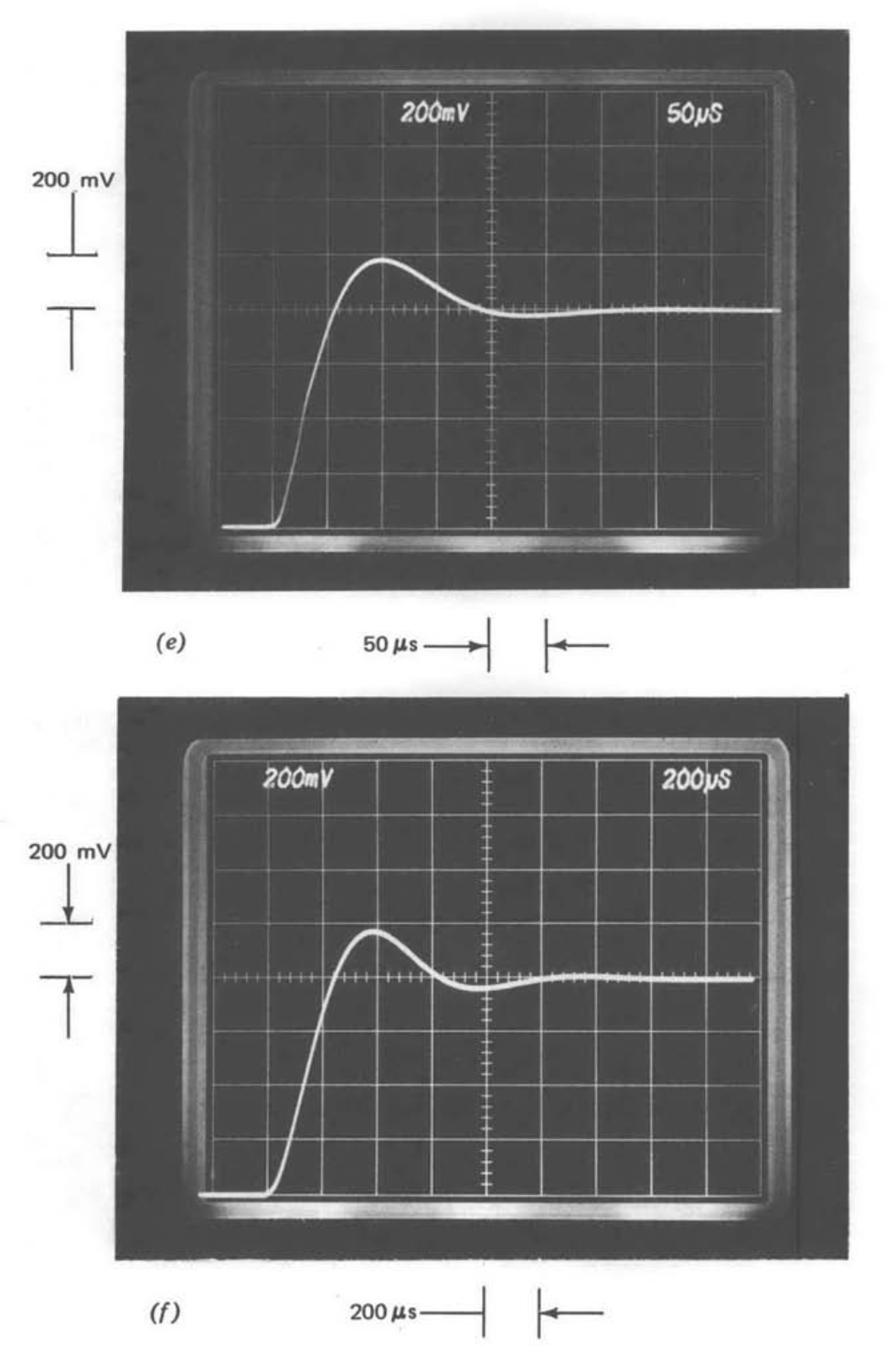
Малюнок 5.17 Відгук підсилювача посилення десяти на крок 80-мВ. (\(a\)) Відсутність компенсації. (\(b\)) Свинець компенсований. (\(c\)) Відставання компенсується. (\(d\)) Знижена\(a_0 f_0\). (\(e\)) Компенсація свинцю в прямому шляху. (\(f\)) Наближення другого порядку до (\(c\)).
На малюнку 5.17\(a\) показана ступінчаста реакція підсилювача посилення десяти без компенсації. Велике перевищення піку і погане демпфування дзвінка відображають низький запас фази системи. Перенесення та демпфування для відведення компенсованих, компенсованих затримкою та зменшеними\(a_0f_0\) випадками (рис. 5.17\(b\)\(c\), 5.17 та 5.17\(d\) відповідно) значно покращуються, як і передбачалося з огляду на набагато більш високі фазові запаси цих з'єднань. Ступінчаста характеристика, отримана при зниженні частоти першого полюса в петлі, не показана, так як вона не відрізняється від малюнка 5.17\(d\).
Певні особливості цих крокових відповідей видно з цифр. Пікове перенапруження, виставлене підсилювачем зі\(a_0f_0\) зменшеним, трохи менше, ніж у підсилювача з компенсацією затримки, що відображає трохи більший запас фази. Аналогічно, час підйому лаг-компенсованого підсилювача дуже трохи швидше, знову ж таки відображаючи вплив відносного запасу фаз на продуктивність цих двох систем з однаковими частотами кросовера. Менший піковий перевищення системи, компенсованої свинцем, не передбачає більшої відносної стабільності для цього підсилювача, а відбувається через вплив провідної мережі на шляху зворотного зв'язку на ідеальне посилення із замкнутим контуром.
На малюнку 5.17\(e\) показана крокова реакція, яка виникає, якщо компенсація свинцю забезпечується прямим шляхом, а не на шляху зворотного зв'язку. Таким чином, передача петлі для цього перехідного відгуку ідентична малюнку 5.17\(b\) (Рівняння\(\ref{eq5.2.16}\)), але шлях зворотного зв'язку для системи, показаної на малюнку 5.17,\(e\) є незалежним від частоти. У той час як компенсація відведення вперед була заборонена постановкою задачі попередніх прикладів, рис. 5.17\(e\) забезпечує більш реалістичну вказівку відносної стійкості, ніж на рис. 5.17\(b\), оскільки рис. 5.17\(e\) виходить з системи з незалежним від частоти ідеальним посиленням. Різниця між цими двома системами з однаковими петлевими передачами виникає через відмінності в замкнутих нульових місцях (див. Розділ 4.3.4).
Пікове перенапруження і відносне демпфування рис. 5.17\(c\) і 5.17\(e\) практично ідентичні, демонструючи, що принаймні для цього прикладу рівні значення фазового запасу призводять до однакової відносної стійкості для систем, що компенсують відведення і лаг. Час підйому малюнка 5.17 приблизно на чверть\(e\) дорівнює показнику малюнка 5.17\(c\), і це співвідношення практично ідентично співвідношенню частот кросовера двох підсилювачів.
Ступінчаста реакція на малюнку 5.17\(f\) є реакцією системи другого порядку з\(\zeta = 0.45\) і\(\omega_n = 8.5 \times 10^3\) радіанами в секунду. Ці значення були отримані за допомогою рис. 4.26\(a\) для визначення апроксимуючої системи другого порядку до лаг-компенсованого підсилювача. Подібність рис. 5.17\(c\) і 5.17\(f\) є ще одним прикладом точності, яка часто виходить при наближенні складних систем першого або другого порядку. Контурна передача для лаг-компенсованої системи (Equation\(\ref{eq5.2.17}\)) включає чотири полюси і один нуль. Однак ця величина має лише однополюсний відкат між\(6.7 \times 10^2\) радіанами в секунду та частотою кросовера, з другим полюсом поблизу кросовера. Таким чином, він може бути добре наближений як система з двома широко відокремленими полюсами, модель, з якої була розроблена Рисунок 4.26.
Пов'язані міркування
Кілька додаткових зауважень щодо відносних переваг різних методів компенсації серії в порядку. Оцінка продуктивності в попередньому прикладі, здається, передбачає переваги для компенсації свинцю. Підсилювач, компенсований свинцем, виглядає вищим, якщо дечутливість на різних частотах, величина коефіцієнта похибки або швидкість перехідного відгуку
використовується в якості показника продуктивності. Крім того, якщо функція передачі свинцю включена в шлях зворотного зв'язку, підсилювач демонструє краще- демпфіровані перехідні реакції, ніж можна отримати з інших типів компенсації, вибраних для отримання еквівалентної фазової запасу. Переваги, пов'язані з компенсацією свинцю, в першу чергу відображають більш високе значення перехресної частоти та відповідно більш високу пропускну здатність із замкнутим контуром, що часто можливо за допомогою цього методу. Слід підкреслити, однак, що пропускна здатність, що перевищує вимоги, зазвичай погіршує загальну продуктивність. Більша пропускна здатність збільшує чутливість до шуму підсилювача і часто призводить до більших проблем стабільності через блукаючу індуктивність або ємність.
Компенсація свинцю зазвичай посилює проблему стабільності, якщо контур також включає елементи, які забезпечують великий негативний зсув фаз в широкому діапазоні частот без відповідного ослаблення величини. (Хоча обмеження фізичної реалізованості виключають елементи, які забезпечують позитивний зсув фаз без збільшення амплітуди, менш корисний зворотний зв'язок, описаний вище, відбувається з тривожною частотою.) Наприклад, розглянемо систему, яка поєднує в собі частотно-незалежне посилення в циклі з\(\tau\) -секундною затримкою часу, наприклад, що забезпечується лінією затримки. Негативним показником контурної передачі для цієї системи є
\[a(s) f(s) = a_0 e^{-s \tau} \nonumber \]
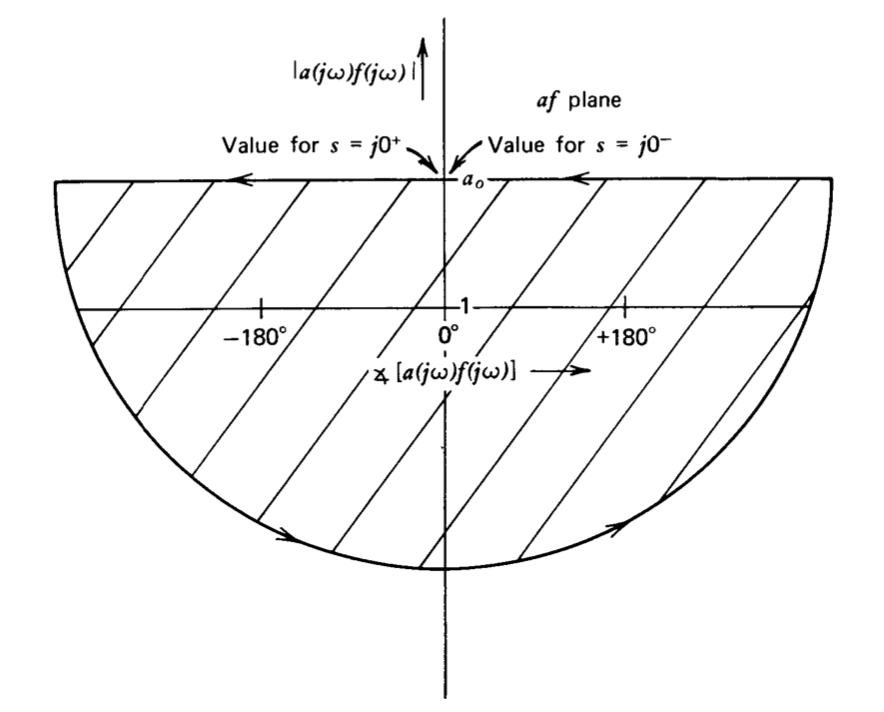
Затримка часу - це елемент, який має величину посилення один на всіх частотах і негативний зсув фаз, який лінійно пов'язаний з частотою. Діаграма Найквіста (рис. 5.18) для цієї системи показує, що вона нестабільна для\(a_0 > 1\). Використання компенсації свинцю сполучає проблему, оскільки позитивний зсув фаз провідної мережі не може протидіяти необмеженому негативному зсуву фаз затримки часу, тоді як збільшення величини функції відведення ще більше знижує максимальну низьку частотну дечутливість відповідно до стабільної роботи.
Правильний підхід полягає у використанні домінуючого полюса для зменшення величини передачі петлі до того, як фазовий зсув затримки часу стане надмірним. Граничний випадок інтегратора (полюс біля початку) працює добре, і ця модифікація призводить до
\[a(s) f(s) = \dfrac{a_0}{s} e^{-s \tau} \nonumber \]
Дечутливість цієї функції нескінченна при d-c. Читач повинен переконати себе, що система абсолютно стабільна при будь-якому позитивному значенні\(a_0 < \pi / 2\tau\), і що хоча б\(45^{\circ}\) фазовий запас виходить з позитивним\(a_0 < \pi /4\tau\).
Використання компенсації затримки вводить тип помилки, який компрометує її значення в деяких додатках. Якщо ступінчаста реакція підсилювача з компенсацією затримки розглядається досить детально, часто виявляється, що він включає тривалий постійний, малоамплітудний «хвіст», який може надмірно збільшити час, необхідний для осідання до невеликої частки кінцевого значення. Аналогічно, хоча коефіцієнт похибки ei може бути досить малим, час, необхідний для того, щоб похибка рампи досягла свого сталого значення, може здатися несумісним з частотою кросовера підсилювача.
В якості допомоги для розуміння цієї проблеми розглянемо систему з\(f(s) = 1\) і
\[a(s) = \dfrac{1000 (0.1 s + 1)}{s (s + 1)}\label{eq5.2.24} \]
Ця передавальна функція є ідеалізованим поданням системи, яка поєднує в собі один домінантний полюс з компенсацією затримки для поліпшення дечутливості. Нуль лаг-мережі розташовується на коефіцієнт 10 нижче перехресної частоти. Функція передачі із замкнутим циклом є
\[A(s) = \dfrac{a(s)}{1 + a(s)f(s)} = \dfrac{(0.1s + 1)}{10^{-3} s^2 + 0.101s + 1} = \dfrac{(0.1s + 1)}{(0.09s + 1)(0.011s + 1)} \nonumber \]
Відповідь цієї системи на одиничний крок легко оцінюється за допомогою методів Лапласа, з результатом
\[v_o (t) = 1 - 1.126 e^{-t/0.011} + 0.126 e^{-t/0.09}\label{eq5.2.26} \]
Цей кроковий відгук досягає 10% від кінцевого значення за 0,02 секунди, що є розумним значенням з огляду на частоту кросовера 100 радіан в секунду системи. Однак час, необхідний для досягнення 1% від кінцевого значення, становить 0,23 секунди через кінцевий член в Рівнянні\(\ref{eq5.2.26}\). Зверніть увагу,\(a(s)\) що якщо змінено на\(100/s\), передавальну функцію з тією ж частотою посилення одиниці, що\(\ref{eq5.2.24}\) і рівняння, і меншою величиною посилення на всіх частотах нижче 10 радіанів в секунду, час, необхідний для того, щоб крокова реакція системи досягла 1% від кінцевого значення, становить приблизно 0,05 другий.
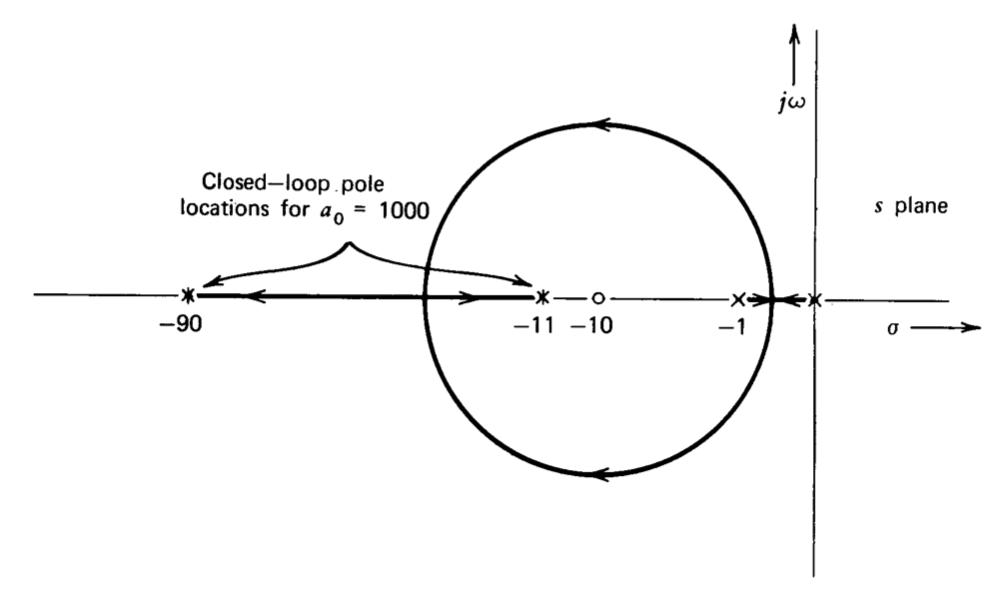
Схема коріння-локуса для системи (рис. 5.19) прояснює ситуацію. Система має нуль із замкнутим контуром з кутовою частотою на рівні 10 радіанів в секунду, оскільки нуль, показаний на схемі, є сингулярністю прямого шляху. Зворотний зв'язок змушує один замкнутий полюс близький до цього нуля. Результуючий близько розташований полюс-нульовий дублет додає довготривалу постійну хвіст до перехідної реакції системи в іншому випадку добре поводиться. Читачеві варто нагадати, що саме цей тип дублета погіршує ступінчасту реакцію погано компенсованого зонда осцилографа. Оскільки лінійні системні відносини вимагають, щоб реакція пандуса була інтегралом крокової реакції, час, необхідний для досягнення кінцевого значення похибки пандуса, аналогічно затримується.
Подібні розрахунки показують, що в міру переміщення функції перенесення лаг далі нижче кросовера, амплітуда хвоста зменшується, але його постійна часу збільшується. Ми робимо висновок, що хоча компенсація затримки є потужною технікою для поліпшення дечутливості, її слід використовувати з обережністю, коли час, необхідний для реакції на крок, щоб оселитися на невелику частку його кінцевого значення або час, необхідний для того, щоб помилка рампи досягла кінцевого значення, обмежений.
Слід підкреслити, що полюс із замкнутим контуром, як правило, буде розташовуватися близько до будь-якого нулю з розімкнутим контуром з частотою розриву нижче частоти кросовера. Таким чином, тип хвоста, пов'язаний з компенсацією затримки, також може призвести до, наприклад, компенсації свинцю, яка часто включає нуль нижче кросовера. Різниця в продуктивності призводить до того, що нуль і полюс із замкнутим контуром, який наближається до нього, щоб сформувати дуплет, зазвичай розташовані близько до частоти кросовера для компенсації свинцю. Таким чином час розпаду результуючого хвоста, яке визначається розглянутим полюсом із замкнутим контуром, не сильно подовжує час осідання системи.
Таблиця 5.1 Порівняння послідовно-компенсуючих методів
| Тип | Особливі міркування | переваги | недоліки |
| Знижений\(a_0 f_0\) | Простота | Найнижча дечутливість. | |
| Створити домінантний полюс | Знизьте частоту існуючого домінуючого полюса, якщо це можливо. Знайдіть на виході регулятор. |
Може поліпшити врівноважений імунітет системи. Зазвичай тип вибирають для регулятора. | Знижує пропускну здатність. |
| Лаг | Знайдіть значно нижче частоти кросовера. | Краща дечутливість, ніж будь-яка з перерахованих вище. | Може додати небажаний «хвіст» до перехідної реакції. |
| Свинець | Знайдіть нуль поблизу частоти кросовера. | Найбільша щільність. Найнижчі коефіцієнти похибки. Найшвидший перехідний відгук. |
Підвищує чутливість до шуму. Не можна використовувати з нерухомими елементами, які сприяють надмірному негативному зсуву фаз. |
Складно розробити узагальнені правила, що стосуються компенсації, оскільки правильний підхід сильно залежить від фіксованих елементів, включених в цикл, від типів передбачуваних входів, від обраного критерію ефективності та від багатьох інших факторів. Незважаючи на це застереження, таблиця 5.1 є спробою узагальнити найважливіші особливості чотирьох типів компенсацій серії, описаних у цьому розділі.
