4.1: ПРОБЛЕМА СТАБІЛЬНОСТІ
- Page ID
- 30938
Обговорення систем зворотного зв'язку, представлених до цього моменту, мовчазно припускало, що досліджувані системи були стабільними. Стабільна система визначається загалом як така, яка створює обмежений вихід у відповідь на будь-який обмежений вхід. Таким чином, стабільність означає, що
\[\int_{-\infty}^{\infty} |v_O (t)| dt \le M < \infty \label{eq4.1.1} \]
для будь-якого введення таких, що
\[\int_{-\infty}^{\infty} |v_I (t)| dt \le N < \infty \nonumber \]
Якщо обмежити наш розгляд лінійними системами, стабільність не залежить від вхідного сигналу, а достатньою і необхідною умовою стійкості є те, що всі полюси функції передачі системи лежать в лівій половині площини s. Ця умова випливає безпосередньо з Рівняння\(\ref{eq4.1.1}\), оскільки будь-які право-напівплоскі полюси сприяють умовам виходу, які зростають експоненціально з часом і, таким чином, є необмеженими. Зауважте, що це визначення передбачає, що система з полюсами на уявній осі нестабільна, оскільки її вихід не обмежений, якщо її вхід не обраний досить ретельно.
Походження проблеми стабільності можна описати інтуїтивно привабливим через несуворі терміни наступним чином. Якщо система зворотного зв'язку виявляє помилку між фактичним і бажаним виходами, вона намагається звести цю помилку до нуля. Однак зміни в сигналі помилки, що виникають в результаті коригувальних дій, не відбуваються миттєво через тимчасові затримки навколо циклу. У системі з високим коефіцієнтом посилення ці затримки можуть спричинити тенденцію до надмірного виправлення. Якщо величина перекорекції перевищує величину початкової похибки, виникає нестабільність. Амплітуди сигналу зростають експоненціально, поки деяка нелінійність не обмежує подальше зростання, в цей час система або насичується, або коливається в постійній амплітуді, яка називається граничним циклом. (Вплив нелінійностей на стаціонарну амплітуду, досягнуту нестабільною системою, досліджено в главі 6.) Конструктор системи зворотного зв'язку повинен завжди стримувати своє бажання забезпечити велику величину і високу одиничну частоту посилення для передачі петлі з певними знаннями про те, що досить високі значення для цих величин незмінно призводять до нестабільності.
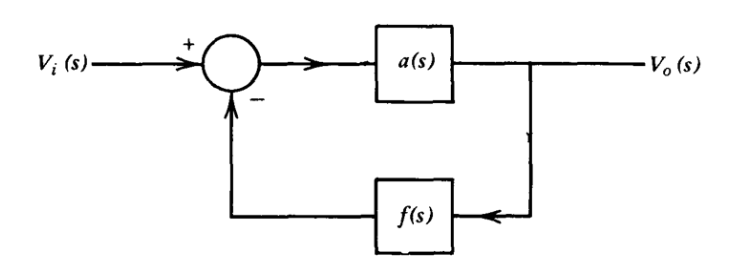
Як конкретний приклад системи з потенційно нестабільною поведінкою розглянемо просту одноконтурну систему типу, показаного на малюнку 4.1, з
\[a(s) = \dfrac{a_0}{(s + 1)^3} \nonumber \]
і
\[f(s) = 1 \nonumber \]
Контурна передача для цієї системи
\[-a(s) f(s) = \dfrac{-a_0}{(s + 1)^3} \nonumber \]
або для синусоїдального збудження,
\[-a(j\omega) f(j\omega) = \dfrac{-a_0}{(j \omega + 1)^3} = \dfrac{-a_0}{-j \omega^3 - 3 \omega^2 + 3j \omega + 1} \label{eq4.1.6} \]
Якщо ми оцінюємо рівняння\(\ref{eq4.1.6}\) на\(\omega = \sqrt{3}\), ми виявимо, що
\[-a (j \sqrt{3}) f(j \sqrt{3}) = \dfrac{a_0}{8} \nonumber \]
Якщо обрана\(a_0\) величина, рівна 8, система має реальну позитивну петлю передачі величиною одиниці для синусоїдального збудження при трьох радіанах в секунду.
Ми можемо підозрювати, що система з петлевою передачею +1 здатна до коливань, і це підозра може бути підтверджена дослідженням функції передачі замкнутого циклу системи с\(a_0 = 8\). У цьому випадку
\[A(s) = \dfrac{a(s)}{1 + a(s) f(s)} = \dfrac{8}{s^3 + 3s^2 + 3s + 9} = \dfrac{8}{(s + 3) (s + j \sqrt{3}) (s - j\sqrt{3})} \nonumber \]
Ця передавальна функція має негативний полюс реальної осі і пару полюсів, розташованих на уявній осі в\(s = \pm j \sqrt{3}\). Аргумент, заснований на властивостях частково-дробових розширень (див. Розділ 3.2.2), показує, що реакція цієї системи на багато загальних (обмежених) перехідних сигналів включає в себе синусоїдальну складову з постійною амплітудою.
Подальше збільшення низькочастотної величини петлі-передачі переміщує полюсну пару в праву половину площини. Наприклад, якщо ми об'єднаємо функцію передачі вперед
\[a(s) = \dfrac{64}{(s + 1)^3} \nonumber \]
з одиничним зворотним зв'язком результуюча функція передачі із замкнутим циклом становить
\[A(s) = \dfrac{64}{s^3 + 3s^2 + 3s + 65} = \dfrac{64}{(s + 5) (s - 1 + j 2\sqrt{3})(s - 1 - j2\sqrt{3})} \nonumber \]
При цьому\(a_0\) значенні для перехідної реакції системи буде включати синусоїдальну складову з експоненціально зростаючою оболонкою.
Якщо динаміка, пов'язана з петлевою передачею, залишиться фіксованою, система буде стабільною тільки при значеннях\(a_0\) менше 8. Така стійкість досягається за рахунок дечутливості. Якщо значення\(a_0 = 1\) використовується так, щоб
\[a(s) f(s) = \dfrac{1}{(s + 1)^3} \nonumber \]
знаходимо всі полюси замкнутого циклу знаходяться в лівій половині площини, так як
\[A(s) = \dfrac{1}{s^3 + 3s^2 + 3s + 2} = \dfrac{1}{(s + 2) (s + 0.5 + j \sqrt{3}/2) (s + 0.5 - j \sqrt{3}/2)} \nonumber \]
в даному випадку.
У певних обмежених випадках достатньо двійкової відповіді на питання стабільності. Однак, як правило, нас цікавить більш кількісна інформація щодо «ступеня» стійкості системи зворотного зв'язку. Часто використовувані заходи відносної стабільності включають пікову величину частотної характеристики, дробове перенапруження у відповідь на ступінчастий вхід, коефіцієнт демпфування, пов'язаний з домінуючою парою полюсів, або зміна певного параметра, який можна допустити, не викликаючи абсолютної нестабільності. Будь-який із згаданих вище заходів відносної стійкості можна знайти шляхом прямих розрахунків, що включають функцію передачі системи. Хоча такі визначення практичні за допомогою машинних обчислень, розуміння роботи системи часто затьмарюється, якщо цей процес використовується. Методи, описані в цьому розділі, покликані не тільки дати відповіді на питання, що стосуються стабільності, але і (і що більш важливо) вказати, як поліпшити продуктивність заводських систем unsatis.
