4.2: КРИТЕРІЙ РОУТА

Тест Раута - це математичний метод, який може бути використаний для визначення кількості нулів многочлена з додатними дійсними частинами. Якщо тест застосовується до знаменника многочлена передавальної функції (його також називають характеристичним рівнянням), відсутність будь-яких право-напівплоских нулів характеристичного рівняння гарантує стабільність системи. Однією з обчислювальних переваг тесту Рута є те, що для застосування тесту не потрібно фактор полінома.

Оцінка стабільності

Тест описаний для многочлена форми

\[P(s) = a_0 s^n + a_1 s^{n - 1} + \cdots + a_{n - 1} s + a_n \label{eq4.2.1} \]

Необхідною, але недостатньою умовою для всіх нулів Рівняння\(\ref{eq4.2.1}\) мають негативні дійсні частини, є те, що всі присутні і що всі вони мають однаковий знак.\(a\) Якщо ця необхідна умова виконується, то з a формується масив чисел наступним чином. (Цей приклад для\(n\) парних. Для\(n\) непарних\(a_n\) закінчується другий ряд.)

\[\begin{array} {ccccccc} {a_0} & {a_2} & {a_4} & \cdot & \cdot & {a_{n - 2}} & {a_n} \\ {a_1} & {a_3} & {a_5} & \cdot & \cdot & {a_{n - 1}} & {0} \\ {\dfrac{a_1 a_2 - a_0 a_3}{a_1} = b_1} & {\dfrac{a_1 a_4 - a_0 a_5}{a_1} = b_2} & {\cdot} & \cdot & \cdot & {\dfrac{a_1 a_n - a_0 \cdot 0}{a_1} = b_{n/2}} & {0} \\ {\dfrac{b_1 a_3 - a_1 b_2}{b_1} = c_1} & {\dfrac{b_1 a_5 - a_1 b_3}{b_1} = c_2} & {\cdot} & \cdot & \cdot & {0} & {0} \\ {\dfrac{c_1 b_2 - b_1 c_2}{c_1} = d_1} & {\cdot} & {\cdot} & \cdot & \cdot & {0} & {0} \\ {\cdot} & {\cdot} & {\cdot} & \cdot & \cdot & {\cdot} & {\cdot} \\ {\cdot} & {\cdot} & {\cdot} & \cdot & \cdot & {\cdot} & {\cdot} \\ {0} & {0} & {\cdot} & \cdot & \cdot & {0} & {0} \end{array} \nonumber \]

У міру розвитку масиву все більше елементів кожного рядка стають нульовими, поки тільки перший елемент\(n + 1\) рядка не буде ненульовим. Загальна кількість змін знаків у першому стовпці тоді дорівнює кількості нулів початкового многочлена, які лежать у правій половині площини.

Використання критерію Раута проілюстровано за допомогою полінома

\[P(s) = s^4 + 9s^3 + 14s^2 + 266s + 260\label{eq4.2.3} \]

Оскільки всі коефіцієнти дійсні та позитивні, задовольняється необхідна умова,\(\ref{eq4.2.3}\) щоб усі корені Рівняння мали від'ємні дійсні частини. Масив є

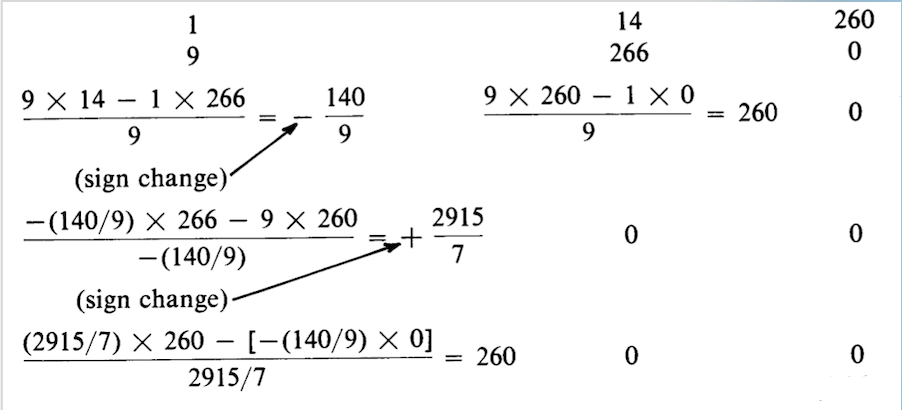
Дві зміни знаків у першому стовпці вказують на два нулі правої півплощини. Цей результат можна перевірити факторингом вихідного полінома, показуючи, що

\[s^4 + 9s^3 + 14s^2 + 266s + 260 = (s - 1 + j5)(s - 1 - j5) (s + 1)(s + 10) \nonumber \]

Другий приклад наводиться поліномом

\[P(s) = s^4 + 13s^2 + 58 s^2 + 306 s+ 260 \nonumber \]

Відповідний масив є

\[\begin{array} {ccc} {1} & {58} & {260} \\ {13} & {306} & {0} \\ {\dfrac{13 \times 58 - 1 \times 306}{13} = \dfrac{448}{13}} & {\dfrac{13 \times 260 - 1 \times 0}{13} = 260} & {0} \\ {\dfrac{(448/13) \times 306 - 13 \times 260}{448/13} = \dfrac{23287}{112}} & {0} & {0} \\ {\dfrac{(23287/112) \times 260 - (448/13) \times 0}{23287/112} = 260} & {0} & {0} \end{array} \nonumber \]

Факторинг перевіряє результат, що для цього многочлена немає нулів правої половини площини, оскільки

\[s^4 + 13s^3 + 58 s^2 + 306 s + 260 = (s + 1 + j5)(s + 1 - j5) (s + 1)(s + 10) \nonumber \]

При застосуванні тесту Рута можуть виникнути два види труднощів. Можливо, що перший елемент в одному рядку масиву дорівнює нулю. При цьому вихідний многочлен множиться на\(s + \alpha\), де a - будь-яке додатне дійсне число, і тест повторюється. Ця процедура ілюструється за допомогою полінома

\[P(s) = s^5 + s^4 + 10s^3 + 10s^2 + 20s + 5 \label{eq4.2.8} \]

Перший елемент третього рядка масиву дорівнює нулю.

\[\begin{array} {ccc} {1} & {10} & {20} \\ {1} & {10} & {5} \\ {0} & {15} & {0} \end{array} \nonumber \]

Складність вирішується множенням Рівняння\(\ref{eq4.2.8}\) на\(s + 1\), поступаючись

\[P'(s) = s^6 + 2s^5 + 11 s^4 + 20 s^3 + 30 s^2 + 25s + 5 \label{eq4.2.10} \]

Масив для Equation\(\ref{eq4.2.10}\) дорівнює

\[\begin{array} {cccc} {1} & {11} & {30} & {5} \\ {2} & {20} & {25} & {0} \\ {1} & {17.5} & {5} & {0} \\ {-15} & {15} & {0} & {0} \\ {-18.5} & {5} & {0} & {0} \\ {10.95} & {0} & {0} & {0} \\ {5} & {0} & {0} & {0} \end{array}\label{eq4.2.11} \]

Оскільки множення на\(s + 1\) не додало жодних нулів у правій половині площини до рівняння\(\ref{eq4.2.8}\), ми робимо висновок, що два правої півплощини нулі, позначені масивом Equation,\(\ref{eq4.2.11}\) повинні міститися у вихідному поліномі.

Друга можливість полягає в тому, що цілий ряд стає нулем. Ця умова вказує на те, що на уявній осі є пара коренів, пара реальних коренів, розташованих симетрично щодо походження, або обидва види пар в початковому многочлені. Терміни в рядку над усім нульовим рядком використовуються як коефіцієнти рівняння в парних ступенях\(s\) званого допоміжного рівняння. Нулями цього рівняння є пари, згадані вище. Допоміжне рівняння можна диференціювати по відношенню до\(s\), а результуючі коефіцієнти використовуються замість рядка з усім нулем для продовження масиву. Цей тип складності ілюструється поліномом

\[P(s) = s^4 + 11s^3 + 11s^2 + 11s + 10 = (s + j)(s - j) (s + 1) (s + 10)\label{eq4.2.12} \]

Масив є

\[\begin{array} {ccc} {1} & {11} & {10} \\ {11} & {11} & {0} \\ {10} & {10} & {0} \\ {0} & {0} & {0} \end{array}\label{eq4.2.13} \]

Допоміжне рівняння

\[Q(s) = 10s^2 + 10\label{eq4.2.14} \]

Коріння рівняння є двома уявними нулями Рівняння\(\ref{eq4.2.12}\). Диференціювання рівняння\(\ref{eq4.2.14}\) та використання ненульового коефіцієнта для заміни першого елемента рядка 4 Рівняння\(\ref{eq4.2.13}\) дає новий масив.

\[\begin{array} {ccc} {1} & {11} & {10} \\ {11} & {11} & {0} \\ {10} & {10} & {0} \\ {20} & {0} & {0} \\ {10} & {0} & {0} \end{array} \nonumber \]

Відсутність знакових змін у масиві перевіряє, що вихідний поліноміал не має нулів у правій половині площини.

Зауважте, що, хоча в правій половині площини немає полюсів із замкнутим контуром, система з характеристичним рівнянням, заданим\(\ref{eq4.2.12}\) Рівнянням, нестабільна за нашим визначенням, оскільки має пару полюсів на уявній осі. Вивчення лише лівого стовпця масиву Routh визначає лише кількість нулів правої півплощини перевіреного полінома. Уявно-осьові нулі можна знайти за допомогою маніпуляцій, пов'язаних з допоміжним рівнянням.

Малюнок 4.2 Блок-схема генератора фазового зсуву.

Допомога дизайну

Критерій Routh найчастіше використовується для визначення стабільності системи зворотного зв'язку. Однак у певних випадках можна отримати більше кількісної проектної інформації, як показано на наступних прикладах.

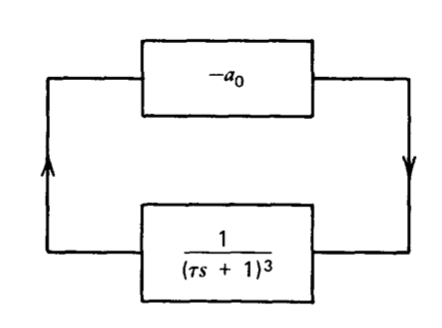
Генератор фазового зсуву може бути побудований шляхом застосування достатньої негативної зворотного зв'язку навколо мережі, яка має три або більше полюсів. Якщо підсилювач з частотно-незалежним коефіцієнтом посилення об'єднаний з мережею з трьома збіженими полюсами, то блок-схема для результуючої системи виглядає так, як показано на малюнку 4.2. Значення\(a_0\) необхідних для витримки коливань може бути визначено за допомогою аналізу Рута. (Тест Раута, застосований до цього прикладу, пропонує обчислювальні переваги порівняно з прямим факторингом, використовуваним для подібної передавальної функції у прикладі Розділу 4.1.)

Дослідження стійкості для малюнка 4.2 ускладнюються тим, що

генератор не має входу; таким чином, ми не можемо використовувати полюси функції передачі вхід-вихід для визначення стабільності. Слід зазначити, що стійкість лінійної системи є властивістю самої системи і, таким чином, не залежить від вхідних сигналів, які можуть бути застосовані до неї. Будь-яка нестабільна фізична система продемонструє свою нестабільність без введення, оскільки втеча поведінка буде стимулюватися завжди присутнім шумом. Навіть в чисто математичній лінійній системі стійкість визначається розташуванням полюсів із замкнутим контуром, причому ці місця явно вводяться незалежними.

Аналіз генератора ініціюється нагадуванням про те, що характеристичне рівняння будь-якої системи зворотного зв'язку - це один мінус його петльової передачі. Тому

\[P(s) = 1 + \dfrac{a_0}{(\tau s + 1)^3} \nonumber \]

У цьому та інших розрахунках за участю характеристичного рівняння можна очистити дроби, оскільки розташування нулів не змінюються цією операцією. Після очищення дробів і ідентифікації коефіцієнтів масив Routh дорівнює

\[\begin{array} {cc} {\tau^3} & {3 \tau} \\ {3 \tau^2} & {1 + a_0} \\ {\dfrac{(8 - a_0) \tau}{3}} & {0} \\ {1 + a_0} & {0} \end{array} \nonumber \]

Припускаючи, що\(\tau\) є додатним, коріння з додатними дійсними частинами зустрічаються для\(a_0 < -1\) (один нуль правої половини площини) та для\(a_0 > +8\) (два нулі правої півплощини).

Аналіз Лапласа показує, що для генерації синусоїдального коливання з постійною амплітудою потрібна пара полюсів на уявній осі. На практиці складна полюсна пара розташовується трохи праворуч від уявної осі. Потім навмисно введена нелінійність може бути використана для обмеження амплітуди коливання (див. Розділ 6.3.3). Таким чином, практична схема генератора виходить с\(a_0 > 8\).

Частоту коливань з\(a_0 = 8\) можна визначити, вивчивши масив з цим значенням для\(a_0\). При цих умовах третій ряд стає всім нулем. Допоміжне рівняння

\[Q(s) = 3\tau^2 s^2 + 9 \nonumber \]

і рівняння має нулі при\(s = \pm j \sqrt{3}/\tau\), що вказує на коливання при\(\sqrt{3}/\tau\) радіанах в секунду для\(a_0 = 8\).

Як другий приклад типу конструкторської інформації, яку можна отримати за допомогою аналізу Routh, розглянемо операційний підсилювач з функцією передачі розімкнутого контуру

\[a(s) = \dfrac{a_0}{(s + 1) (10^{-6} s + 1) (10^{-7} s + 1)} \nonumber \]

Передбачається, що цей підсилювач підключений як неінвертуючий підсилювач з одиничним коефіцієнтом посилення, і ми хочемо визначити діапазон значень ao, для якого всі полюси замкнутого циклу мають реальні частини більш негативні, ніж\(-2 \times 10^5 \text{sec}^{-1}\). Ця умова при розташуванні полюса із замкнутим контуром передбачає, що будь-яка імпульсна реакція системи згасне принаймні так само швидко, як\(K e^{-2 \times 10^5 t}\) після того, як збуджуючий імпульс повернеться до нуля. Константа залежить\(K\) від умов в той момент, коли вхід стає нулем.

Характерне рівняння для підсилювача є (після скидання незначних членів)

\[P(s) = 10^{-13} s^3 + 1.1 \times 10^{-6} s^2 + s + 1 + a_0 \label{eq4.2.20} \]

Для того, щоб визначити діапазон ao, для якого всі нулі цього характеристичного рівняння мають дійсні частини більш від'ємні\(-2 \times 10^5 \text{sec}^{-1}\), потрібно лише зробити зміну змінної в Рівнянні\(\ref{eq4.2.20}\) і застосувати критерій Рута до модифікованого рівняння. Зокрема, застосування тесту Рута до полінома, отриманого заміщенням

\[\lambda = s + c \nonumber \]

визначить кількість нулів початкового полінома з дійсними частинами більш позитивними\(-c\), ніж, оскільки ця заміна зміщує сингулярності в\(s\) площині вправо на величину,\(c\) оскільки вони відображені в\(\lambda\) площині. Якщо вказана заміна проводиться з\(c = 2 \times 10^5 \text{sec}^{-1}\), Рівняння\(\ref{eq4.2.20}\) стає

\[P(\lambda) = 10^{-13} \lambda^3 + 10^{-6} \lambda^2 + 0.57 \lambda - 1.57 \times 10^5 + a_0 \nonumber \]

Масив Routh дорівнює

\[\begin{array} {cc} {10^{-13}} & {0.57} \\ {10^{-6}} & {-1.57 \times 10^5 + a_0} \\ {0.59 - 10^{-7} a_0} & {0} \\ {-1.57 \times 10^5 + a_0} & {0} \end{array} \nonumber \]

Цей масив показує, що Eqn\(\ref{eq4.2.20}\) має один нуль з реальною частиною більш позитивною\(a_0 < 1.57 \times 10^5\), ніж\(-2 \times 10^5 \text{sec}^{-1}\) for, і має два нулі праворуч від ділильної лінії для\(a_0 > 5.9 \times 10^6\). Відповідно, всі нулі мають реальні частини більш негативні, ніж\(-2 \times 10^5 \text{sec}^{-1}\) тільки для

\[1.57 \times 10^5 < a_0 < 5.9 \times 10^6 \nonumber \]