3.4: MOS транзистор

Last updated
Save as PDF

Page ID: 34452

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

CNX йде на пенсію! Підручники OpenStax завжди будуть доступні на сайті openstax.org. Створений спільнотою вміст залишатиметься доступним до серпня 2022 року, а потім буде переміщений до Інтернет-архіву. Дізнайтеся більше тут

Тепер ми можемо повернутися до нашої початкової структури, показаної у вступі до MOSFET, тільки цього разу ми додамо оксидний шар, структуру воріт і іншу батарею, щоб ми могли інвертувати область під воротами і з'єднати дві n-області разом. Ми також визначимо деякі назви для частин структури, тому ми будемо знати, про що ми говоримо. З причин, які будуть зрозумілі пізніше, називаємо n-область, підключену до негативної сторони батареї джерелом, а іншу - стоком. Заземлимо джерело, а також підкладку п-типу. Додаємо дві батареї:\(V_{\text{gs}}\) між затвором і джерелом, і\(V_{\text{ds}}\) між зливом і джерелом.

Малюнок\(\PageIndex{1}\): Зміщення транзистора MOSFET

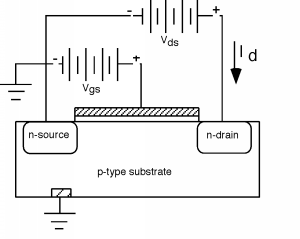
MOSFET транзистор із заземленою підкладкою p-типу знизу та оксидним шаром та затвором зверху. У верхній частині підкладки є дві області n-типу: заземлений джерело знаходиться зліва, а стік - праворуч. Джерело напруги V_GS підключає джерело до затвора, причому позитивний кінець ближче до затвора. Джерело напруги V_DS підключає джерело до стоку, причому позитивний кінець ближче до стоку. Струм i_D тече в стік по цьому з'єднанню. — Малюнок\(\PageIndex{1}\): Зміщення транзистора MOSFET

Буде корисно, якщо ми також зробимо ще один ескіз, який дає нам перспективний вигляд пристрою. Для цього ми знімаємо затвор і оксид, але ми уявимо, що ми застосували напругу більше, ніж\(V_{T}\) до затвора, тому існує область n-типу, яка називається каналом, який з'єднує два. Будемо вважати, що область каналу має довжину\(L\) і ширину\(W\), як показано на малюнку\(\PageIndex{2}\).

Малюнок\(\PageIndex{2}\): Інверсійний канал і його опір

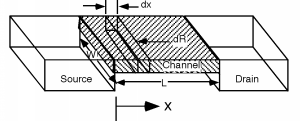
Перспективний вид джерела зліва і стоку праворуч, обидва показані у вигляді прямокутних призм однакового розміру. Прямокутна призма, верх якої знаходиться врівень з верхівками джерела і стоку, але коротше по висоті, утворює канал, що з'єднує джерело і стік. Канал має довжину L і ширину W; відстань по горизонталі від лівого кінця каналу задається як х. розмічається смуга каналу, з невеликою довжиною dx і опором dR. — Малюнок\(\PageIndex{2}\): Інверсійний канал і його опір

Далі ми хочемо поглянути на невелику ділянку каналу та знайти його опір\(dR\), коли маленька секція\(dx\) довга. \[dR = \frac{dx}{\sigma_{s} W}\]

Тут ми ввели дещо іншу форму для нашої формули опору. Зазвичай у нас буде простий\(\sigma\) знаменник, і площа\(A\) для площі поперечного перерізу каналу. Виявляється дуже важко розібратися, що таке площа поперечного перерізу каналу, однак. Електрони, що утворюють інверсійний шар, натовпу в дуже тонкий аркуш поверхневого заряду, який дійсно має невелику або зовсім не товщину, або проникнення в підкладку.

Якщо, з іншого боку, розглядати поверхневу провідність (одиниці виміру\(\mathrm{mhos} = \mho = \Omega^{-1}\))\(\sigma_{s}\), де\[\sigma_{s} = \mu_{s} Q_{\text{chan}}\]

то у нас буде вираз, який ми можемо оцінити. Тут,\(mu_{s}\) є поверхнева рухливість, з одиницями\(\frac{\mathrm{cm}^2}{\mathrm{V} \cdot \mathrm{sec}}\). Ми\(\mu\) зіткнулися з попередніми главами, коли ми будували нашу просту модель провідності. Саме величина представляла пропорційність між середньою швидкістю носія і електричним полем. \[\bar{v} = \mu E\]\[\mu = \frac{q \tau}{m}\]

Поверхнева рухливість - це величина, яка повинна бути виміряна для певної системи, і зазвичай це лише число, яке дається вам. Щось навколо\(300 \ \frac{\mathrm{cm}^2}{\mathrm{V} \cdot \mathrm{sec}}\) є правильним для кремнію. \(Q_{\text{chan}}\)називається поверхневою щільністю заряду або щільністю каналу заряду і вона має одиниці виміру\(\frac{\mathrm{Coulombs}}{\mathrm{cm}^2}\). Це як лист шихти, який відрізняється від насипної щільності заряду, який має одиниці\(\frac{\mathrm{Coulombs}}{\mathrm{cm}^2}\). Зверніть увагу, що:\[\begin{array}{l} \frac{\mathrm{cm}^2}{\mathrm{Volt} \cdot \mathrm{sec}} \frac{\mathrm{Coulombs}}{\mathrm{cm}^2} &= \frac{\frac{\mathrm{Coul}}{\mathrm{sec}}}{\mathrm{Volt}} \\ &= \frac{I}{V} \\ &= \mho \end{array}\]

Виявляється, досить просто отримати вираз для того\(Q_{\text{chan}}\), щоб поверхнева щільність заряду в каналі. Для будь-якого заданого напруги затвора ми знаємо\(V_{\text{gs}}\), що щільність заряду на затворі задається просто як:\[Q_{g} = c_{\text{ox}} V_{\text{gs}}\]

Однак, поки\(V_{\text{gs}}\) напруга затвора не стане більшою, ніж\(V_{T}\) ми не створюємо ніяких мобільних електронів під воротами, ми просто нарощуємо область виснаження. Визначимо\(Q_{T}\), як заряду на ворота необхідно дістатися до порога. \(Q_{T} = c_{\text{ox}} V_{T}\). Будь-який заряд, доданий до\(Q_{T}\) воріт вище, відповідає заряду\(Q_{\text{chan}}\) в каналі. Таким чином, легко сказати:\[Q_{\text{chan}} = Q_{g} - Q_{T}\]

або \[Q_{\text{chan}} = c_{\text{ox}} \left(V_{g} - V_{T}\right)\]

Таким чином, поставивши рівняння\(\PageIndex{8}\) і рівняння\(\PageIndex{2}\) в рівняння\(\PageIndex{1}\), ми отримуємо:\[d(R) = \frac{d(x)}{\mu_{s} c_{\text{ox}} \left(V_{\text{gs}} - V_{T}\right) W}\]

Якщо озирнутися назад на рисунок\(\PageIndex{1}\), то ви побачите, що ми визначили струм, що\(I_{d}\) протікає в стік. Той струм протікає через канал, а значить, через наше невелике\(dR\) інкрементний опір, створюючи падіння\(d \left(V_{c}\right)\) напруги на ньому, де\(V_{c}\) знаходиться напруга каналу. \[\begin{array}{l} d \left(V_{c} (x)\right) &= I_{d} d(R) \\ &= \frac{I_{d} d(x)}{\mu_{s} c_{\text{ox}} \left(V_{\text{gs}} - V_{T}\right) W} \end{array}\]

Давайте перемістимо знаменник вліво, і інтегруємо. Ми хочемо зробити наш інтеграл повністю уздовж каналу. Напруга на каналі\(V_{c} (x)\) йде\(V_{\text{ds}}\) зліва\(0\) направо. При цьому\(x\) збирається від\(0\) до\(L\). Таким чином, наші межі інтеграції будуть\(0\) і\(V_{\text{ds}}\) для інтеграла напруги\(d \left(V_{c} (x)\right)\) і від\(0\) до\(L\) для інтеграла\(dx\). \[\int\limits_{0}^{V_{\text{ds}}} \mu_{s} c_{\text{ox}} \left(V_{\text{gs}} - V_{T}\right) W \ d V_{c} = \int\limits_{0}^{L} I_{d} \ dx\]

Обидва інтеграли досить тривіальні. Давайте поміняємо порядок рівнянь, оскільки ми зазвичай хочемо\(I_{d}\) як функцію прикладених напруг. \[I_{d} L = \mu_{s} c_{\text{ox}} W \left(V_{\text{gs}} - V_{T}\right) V_{\text{ds}}\]

Тепер ми просто ділимо обидві сторони на\(L\), і\(I_{d}\) в кінцевому підсумку ми отримуємо вираз для струму стоку з точки зору напруги сток-джерела\(V_{\text{ds}}\)\(V_{\text{gs}}\), напруги затвора та деяких фізичних атрибутів МОП-транзистора. \[I_{d} = \left(\frac{\mu_{s} c_{\text{ox}} W}{L} \left(V_{gs} - V_{T}\right) \right) V_{ds}\]